Universal quantum circuit evaluation on encrypted data using probabilistic quantum homomorphic encryption scheme*

Jing-Wen Zhang(张静文) Xiu-Bo Chen(陈秀波) Gang Xu(徐刚) and Yi-Xian Yang(杨义先)

1Information Security Center,State Key Laboratory of Networking and Switching Technology,

Beijing University of Posts and Telecommunications,Beijing 100876,China

2School of Information Science and Technology,North China University of Technology,Beijing 100144,China

Keywords: quantum homomorphic encryption,universal quantum circuit,non-maximally entangled state,security

1. Introduction

With the rapid development of the network, it makes information transmission fast and provides a large quantity of information on the Internet. Therefore, the privacy protection of sensitive information is particularly important. When some clients who do not have the computational power cannot calculate their own confidential information,the information needs to be encrypted and sent to a server with rich resources and powerful functions to operate. Homomorphic encryption provides an effective way to process and calculate encrypted data without revealing the contents of the privacy information. Reviewing the classical homomorphic encryption (HE), the idea was first presented by Rivestet al.[1]in 1978. It was widely studied and applied,and can only achieve the additively HE schemes. Until a breakthrough was made in 2009,Gentry[2]found and conducted an in-depth study of the fully homomorphic encryption (FHE) scheme based on nonstandard computational assumptions, thereby giving the multiplicatively HE scheme. Subsequently, many optimization and improvement schemes for FHE have been proposed.[3-7]With the development of classical homomorphic encryption,many achievements have been made and a large amount of related researches have also been sparked, such as delegating computation,[8-11]functional encryption,[12,13]and obfuscation.[14]

At the same time,this research has drawn attention in the field of quantum information.Quantum homomorphic encryption is that the client delegates quantum computation on the encrypted data to the server,that is,the server performs quantum computation on the ciphertext,and the result is consistent with a valid ciphertext after performing this computation on the original plaintext. In other words, the server implements quantum computation without decrypting, and the client decrypts the computation results to obtain the quantum computation on the original data. In 2012,Rohdeet al.[15]described a limited quantum homomorphic encryption scheme with the boson scattering model and quantum walks to complete the restricted quantum computation.The concept of quantum homomorphic encryption (QHE) and quantum fully homomorphic encryption (QFHE) was proposed by Liang[16]in 2013. In Liang’s scheme,the symmetric QHE scheme was constructed.Then,inspired by the tripartite blind quantum computation,[17]Liang proposed a QHE scheme through the use of universal quantum circuit.[18]It permits universal quantum computation on encrypted quantum state without decryption. Nevertheless, in 2014, Yuet al.[19]found that there is a limitation on the QHE scheme with information-theoretically-secure, that is, deterministic QHE with perfect information theoretic security will certainly lead to exponential overhead. This had led to more in-depth discussions among researchers on QFHE schemes that enable to complete universal quantum computation. In the same year, an effective method was proposed by Fisheret al.[20]By using single photons and linear optics,it is experimentally proved that arbitrary quantum computation can be adequately implemented through a set of quantum gates with few extra resources. Based on the modification of the above work, Broadbent and Jeffery (BJ15) completed the limited number of non-Clifford gates evaluation by presenting two instructive and secure QHE schemes.[21]The formal definitions of QHE and QFHE were given,and the definition of quantum indistinguishability under chosen plaintext attack was also given. In 2016, Duleket al.[22]extended the non-Clifford gate circuit in BJ15 to arbitrary polynomial-sized quantum circuits. A novel compact QFHE scheme was given that could effectively correct the errors in the T-gate evaluation of encrypted quantum data. Based on the research results of Duleket al.,[22]Alagicet al.[23]constructed a QFHE scheme with verification to generate a classical computation log, so that the user can verify the homomorphic quantum computation on the ciphertext. It put forward a new direction for future research,that is,more QFHE schemes with certain properties could be found.

In 2016, Tanet al.[24]presented a private-key QHE scheme by using the thoughts of group theory. The scheme supported a broad range of quantum computation tasks and limited the information that attackers can access to ensure information theoretic security. After exhaustive research,Ouyang and Tanet al.[25]designed a QHE from quantum codes that allows for the evaluation of a finite number of non-Clifford gates included in the quantum circuits and has entropy security which is independent of the adversary’s computational power. Moreover, this scheme demonstrated that the model of entropy security is stronger than the security model in BJ15. In 2018, Mahadev[26]constructed the first leveled FHE scheme with classical keys for quantum circuits using quantum capable scheme. It makes blind delegate quantum computations possible to the trusted quantum server, while a malicious server cannot get any information from this process.In addition to the above schemes, there are many results related to QHE schemes.[27-31]

The evaluation of the non-Clifford gates will be subject to errors, leading to the failure of the expected computation results in the QHE scheme. As a result,it is an essential and difficult problem to correct the errors of non-Clifford gate evaluation. The schemes in Refs. [21-25] are all leveled QHE schemes,in which the BJ15 framework utilizes the maximum entangled state to process the correction required for the evaluation of the non-Clifford gates until the decryption phase. In other words, the problem of implementing the QHE scheme via the maximum entangled channel has been studied. As a quantum auxiliary resource,different classes of states are considered to be able to complete the correction of non-Clifford gate evaluation errors in the QHE scheme. Since in the realistic environment, a quantum system is open and usually interacts with the surrounding environment, causing the maximal entangled quantum channel tends to degenerate into the non-maximally entangled quantum channel. Also,it may happen that the source does not produce perfect maximally entangled states rather non-maximally entangled pairs. It has become clear that the non-maximally entangled state is not only relatively well prepared, but also shows evident advantages to implement quantum communication protocols in a specific physical system. For example,three-qubit non-maximally entangled state are used as a resource to attain optimal controlled quantum teleportation fidelity,which essentially lowers the requirements of quantum channels.[32]And,for an amplitude damping channel, it was shown that optimal entanglement negativity is obtained only by a non-maximally entangled state.[33]Hence, it is important to investigate the QHE scheme by utilizing the non-maximally entangled state. The pre-shared non-maximally entangled states are used as auxiliary resources to correctly and safely complete the two-party QHE scheme,while lowering the requirements of the quantum channel. This work is of great importance to the experimental realization of the QHE scheme under inevitable noisy effects.

In this paper, we initially introduce non-maximally entangled states as auxiliary resources to correct the erroneousP-gate occurring in the non-Clifford gate evaluation.The arbitrary quantum computation can be performed on the encrypted data and the privacy of data is maintained. Then,unlike other schemes explicated from the perspective of algorithm,we give the process of two-party probabilistic quantum homomorphic encryption scheme from the viewpoint of application. Finally,this scheme has a good performance in terms of security.

The structure of this paper is organized as follows. In Section 2, some preliminary knowledge including quantum computation, quantum one-time pad and quantum homomorphic encryption are introduced. We present our QHE scheme in Section 3. The main idea and the specific process of the scheme are introduced in detail. In Section 4, the security of the scheme is analyzed and discussed.Our work and prospects for future research are summarized in Section 5.

2. Preliminaries

In this section, we provide a detailed introduction to the preliminaries,which helps us to have better understandings of our work. At the same time, the basic definition and related properties of QHE are given. Through these preliminaries, it will be smoother to describe our scheme.

2.1. Quantum computation

A quantum composite system consists of two or more different physical systems. In many cases of quantum mechanics,it is necessary to work with multiparticle states. The quantum state in the composite system can be expressed as the tensor product form of the quantum states in two subsystems,such as|φA〉|φB〉. If there are two single qubits that cannot be written as tensor product form,i.e.,|φ〉/=|a〉|b〉, then|φ〉is known as entangled state. Quantum entanglement is a property of composite systems which has a significant role in quantum computation.[34]It is also one of the main properties used in this paper. Quantum entanglement can be generated under control in different quantum systems, which reflects nonclassical strong correlation and non-locality in two or more quantum systems. In the processing of quantum information,entangled quantum states are often used as quantum channels.The family of two-qubit entangled states is referred to as Bell states in bipartite system,which can be transformed into each other through local operations and classical communication(LOCC). They are also called EPR states, and the forms are as follows:

Another fundamental assumption of quantum mechanics suggests that the evolution of a closed quantum system can be characterized by the unitary operator.Common unitary singlequbit operators include Pauli operators and Hadamard gate,where the Pauli operators are denoted byσ0,σx,σy,andσz.[35]Their forms and circuit diagram representations are given in the following expressions:

In addition to the quantum logic gates described above,phase shift gate and controlled-NOT gate are also common,

The entire Clifford group circuit can be generated from these gates,but non-Clifford gate,such asT-gate,needs to be added to simulate universal quantum circuit,

In a classic computer, the circuit consists of logic gates and wires, where the logic gates are responsible for the processing of the information and the wires are used for the transmission of the information. Quantum circuits consist of quantum gates operated on qubits. Each wire in a quantum circuit may not correspond to a physical connection,but to a physical particle transformation in a period of time or a physical particle moving from one location to another in space. A quantum circuit(QC)withn-qubit input andm-qubit output,from left to right represents the transfer process of quantum states in time or space.

2.2. Quantum one-time pad

In classical cryptography, the security of encryption and decryption usually depends on the assumption of computational intractability, while in quantum cryptography, the security of quantum cryptography depends on the information theoretic security of quantum mechanical properties. In the context of quantum data, the encryption process of information can be depicted as follows by using the quantum one-time pad(QOTP).

Alice has a set ofKoperations{Uk}, in which each element is an unitary matrix of 2n×2nand the occurrence probability of each element is 1/22n,acting on the quantum information ofnqubits. A new encryption key is generated each time the qubit is encrypted. The encrypted quantum information would become a completely mixed state, so it is meaningless for Eve to get a complete quantum state,which guarantees the security of quantum information. For the input quantum stateρcarrying information, applying a random Pauli operator to the information state will get the cipher stateσ, which is the completely mixed state,[36]where (a,b) are the key to the pad. Pauli operatorsXandZare chosen uniformly at random to encrypt the quantum information.

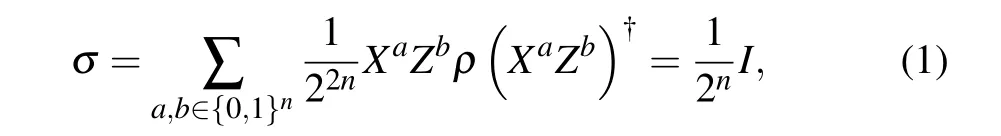
2.3. Quantum homomorphic encryption

This subsection introduces some definitions of quantum homomorphic encryption,homomorphism,compactness,quantum fully homomorphic encryption. For a deeper understanding of these definitions,refer to Ref.[21].

Definition 1(quantum homomorphic encryption) Here we introduce the QHE for asymmetric-key,which includes the following four algorithms:

(i)Key GenerationQHE.KeyGen(1κ)→(pk,sk,ρevk),whereκ ∈Nis the security parameter,pkis the classical public key for encrypting quantum information,skis the classical private key for decrypting,ρevkis the quantum evaluation key for evaluating circuits on the encrypted quantum information.

(ii)EncryptionQHE.Encpk(ρ)→σ. For the input quantum plaintextρ, it is encrypted into the quantum ciphertextσusing the public keypk.

(iii)EvaluationQHE.EvalQCρevk(σ)→σ′,whereQCrepresents any quantum evaluation circuit that acts on the encrypted ciphertextσand outputs a ciphertext quantum stateσ′. The evaluation keyρevkis consumed during the process.This ciphertext is identical to the result of the evaluation circuit acting on the plaintext and then encrypting.

(iv)DecryptionQHE.Decsk(σ′)→ρ′. For the ciphertextσ′, it is decrypted with the private keyskto obtainρ′as the calculation result of the evaluation algorithm acting on the original plaintextρ.

Definition 2(homomorphism) For any quantum circuitQCand the input quantum plaintextρ, a QHE scheme satisfies homomorphism if there exists a negligible functionηsuch that

whereΦQCis the quantum channel that is induced by the quantum circuitQC.

Definition 3(compactness) A QHE scheme is compact if the complexity of the decryption algorithm does not depend on the size of the evaluation circuit. That is, for any quantum circuitQCand ciphertextσ,QHE.Decis applied toQHE.EvalQC(σ). There exists a polynomialp(κ) such that the complexity of this computational process is at mostp(κ).

Definition 4(quantum fully homomorphic encryption)If the QHE scheme satisfies both homomorphism and compactness for all quantum circuits on some universal gate sets,it is a quantum full homomorphic encryption scheme.

3. Our scheme

In this section, based on the model of BJ15, we propose a novel probabilistic quantum homomorphic encryption(PQHE)scheme for universal quantum circuit.Before describing our PQHE scheme,the main idea is given by utilizing the non-maximally entangled state to complete the evaluation of non-Clifford gates. It will be helpful to the proposal of our scheme.

3.1. Main idea

Without decrypting the encrypted data, quantum homomorphic encryption gives a feasible way to perform arbitrary computational evaluations. In the construction of QHE scheme, at least one non-Clifford gate should be added to achieve universality for quantum circuits. However, it is always the focus and barrier of the research to deal with the errors in the evaluation of non-Clifford gates.T-gate,i.e.,“8/π”gate,is the first non-Clifford gate to be known. When the homomorphic evaluation ofT-gate is performed on the quantum state encrypted by QOTP, the output will contain an unexpectedPerror,In order to obtain the quantum state expected by the evaluator,the error must be corrected. The user decrypts the corrected quantum state to acquire the result of performingT-gate calculation on the initial plaintext.

However, the maximum entangled state is considered to be extremely difficult to prepare in a specific physical system. During the preparation of the maximum entangled state,it must be affected by some factors, such as physical equipment,noise and decoherence. Therefore,our scheme extends the BJ15 scheme under the wise usage of the pre-shared nonmaximally entangled states as auxiliary resources to probabilistically correct the erroneousP-gate. Although the probability of success in correcting errors is decreased,it is meaningful from the perspective of experimentally implementing the QHE scheme. The universal quantum circuit with a finite number of non-Clifford gates can be applied on the encrypted quantum state in the evaluation stage.

The major idea of our scheme is that when performing theT-gate evaluation,the state|Φ〉is introduced which is the non-maximally entangled state given by

wheremandnare complex numbers and satisfy the normalization condition|m|2+|n|2=1. Then, the CNOT operation is applied on the non-maximally entangled state with the evaluation circuit. The auxiliary particle is introduced by the part of the circuit’s output. After the definedUoperation,the measurement is made. When the final measurement result is|0〉,theP-gate error is successfully corrected. Otherwise, error correction fails. This process is minutely illustrated in Fig.1.

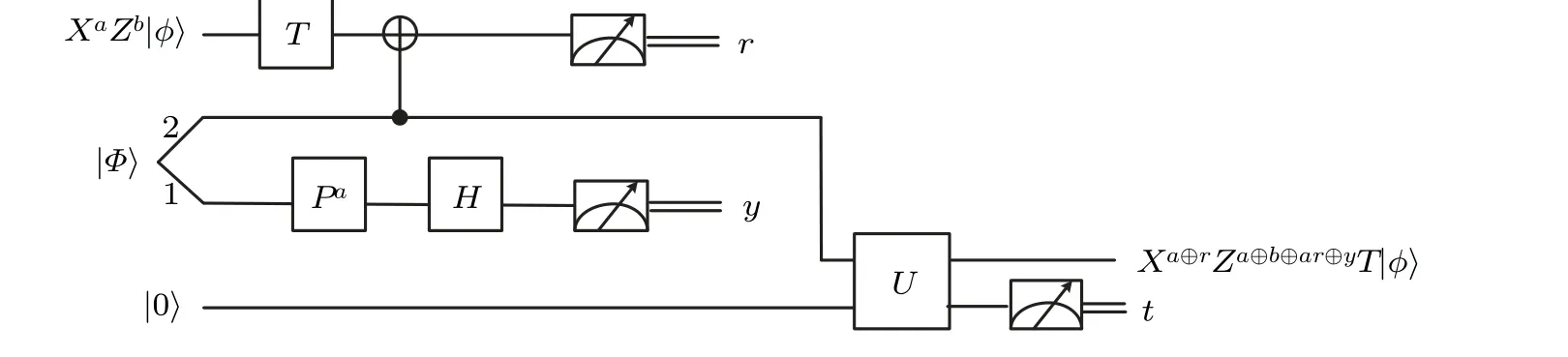
Fig.1. The homomorphic evaluation of our scheme for T-gate.

As shown in Fig.1,the quantum state is|φ〉=α|0〉+β|1〉which will be encrypted by using QOTP,that is,the initial state is encrypted byXaZb,whereaandbare random classical bits(a,b ∈{0,1}). The state will be|φ0〉=XaZb|φ〉and the following four cases are obtained:

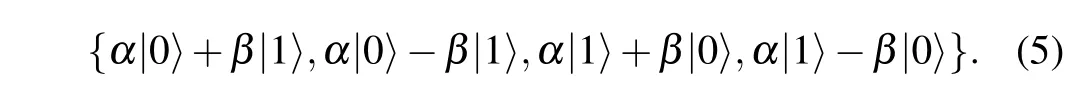
When the firstT-gate appears in the evaluation circuit,theTgate will be applied to the ciphertext,|φ1〉=TXaZb|φ〉. And the encrypted state(5)will become

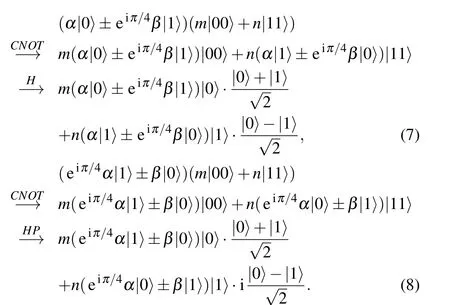
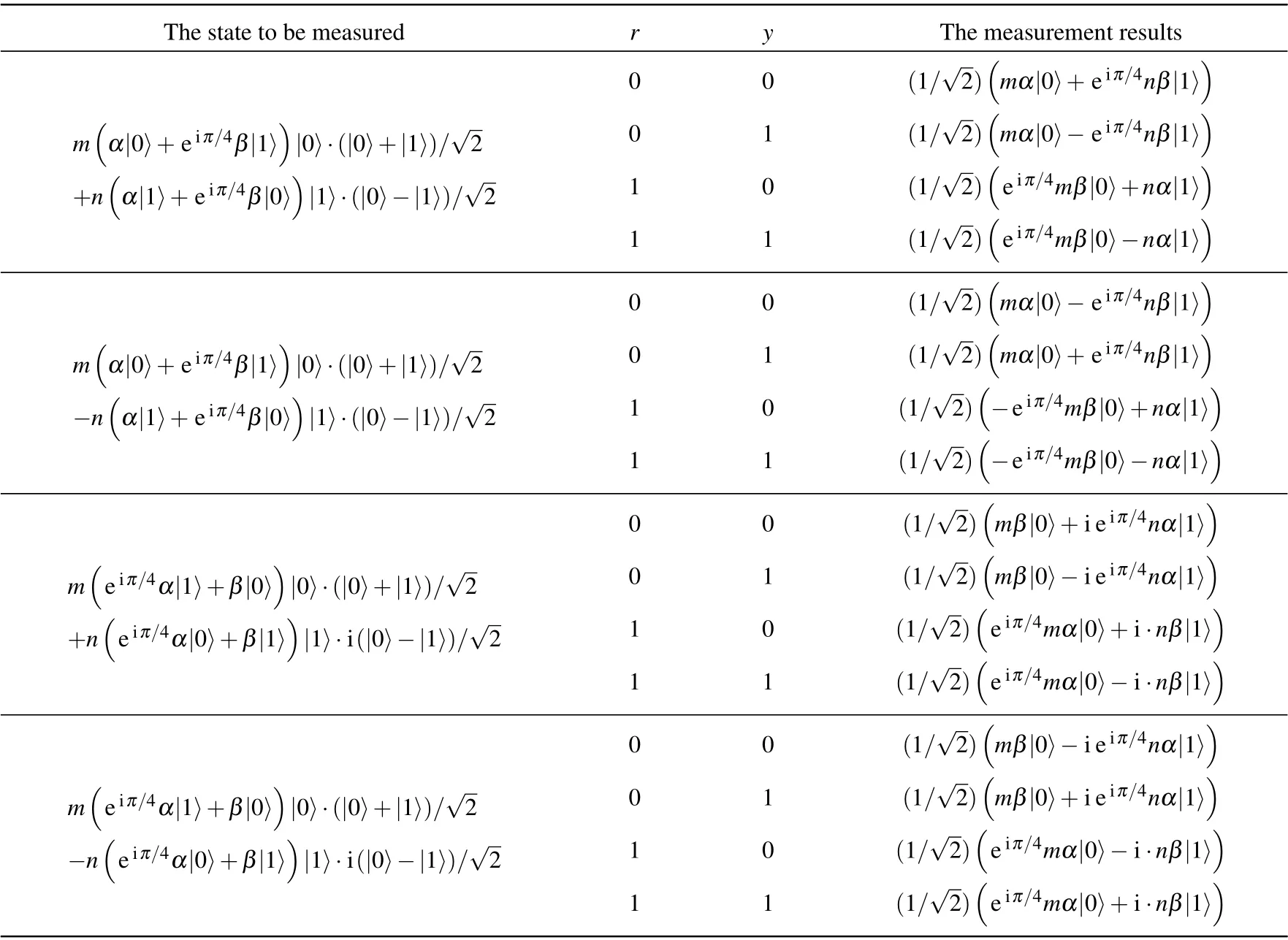
Table 1. Measurement results of the target qubit and the second particle of the non-maximally entangled state.

After the above operation is completed, the measurement will be made in the basis{|0〉,|1〉}. The measurement results of the target qubit and the second particle of the non-maximally entangled state will be two classical bits that recorded asrandyrespectively. In Table 1,the values of the measurement results are displayed substantially which all hold up to an irrelevant global phase.

Through the above series of operations,the coefficient of the state will contain the uncertain valuesmandn. In order to attain the desired result ofT-gate acting on the encrypted state, it will be required to introduce an auxiliary particle|0〉and perform the defined unitary operation that denoted asU,where

The final state Eq.(11)is measured. If the measurement result is|0〉, theP-gate error is successfully corrected. The desired result of the firstT-gate acting on the encrypted state is obtained,which isTXaZb|φ〉=α|0〉+eiπ/4β|1〉(a=0,b=0)in the example. This result is also consistent with

3.2. Our PQHE scheme

In this section, we will specifically present our PQHE scheme. From the perspective of application, there is a clear division of the computations between the client and the server,as well as the determined access rights to the keys and data.Our scheme is a novel two-party PQHE scheme which allows for arbitrary quantum computation within a large class of quantum circuits. Here,the quantum circuit contains Clifford group gates and a finite number of non-Clifford group gates(i.e.,T-gates). In this scheme,firstly,the client randomly generates an encryption key that will be only used once through the key generation algorithm. The private data is encrypted by using QOTP to guarantee the information theoretic security.The encrypted data and the predetermined evaluation circuit are transmitted to the server. Secondly, the server evaluates the received encrypted data according to the sequence of gate operations in the evaluation circuit without decryption. And the evaluated data is returned to the client. Finally, the client generates the decryption key by utilizing the key update rules according to the order of the evaluation circuit and the private key it holds. The evaluated data will be decrypted to get the expected result of the evaluation operation on the original private data. Figure 2 depicts it explicitly.

Fig.2. Evaluation of our PQHE scheme for T-gate.

The following process will describe our two-party PQHE scheme by step.

Step 1PQHE.KeyGen →ek= (a,b), wherea,b ∈{0,1}. The quantum state to be encrypted is|φ〉=α|0〉+β|1〉. The client performs a key generation algorithm to generate a random encryption keyekthat is only used once. The quantum circuitQCEvalintended to be performed on the data will be confirmed corresponding to the sequence of gate operations from the setΓ={X,Z,H,P,CNOT}and theT-gates.It will be used to implement universal quantum circuit evaluation on encrypted data.

Step 2By using the keyek, the encrypted private data takes the form of

Assume that the evaluation circuitQCEvalcontainsNquantum gatesGi(i= 1,...,N). WhenGi ∈Γ, the client will transmit the encrypted dataXaZb|φ〉and evaluation circuitQCEvalto the server through the channel. When aT-gate is included in the evaluation circuit, in addition to the abovementioned data and circuit, the client needs to pre-share a non-maximally entangled state with the server and its form is|Φ〉=m|00〉+n|11〉(|m|2+|n|2=1).

Step 3The server with computational power performs the corresponding operations on the encrypted dataXaZb|φ〉in the order of the evaluation circuitQCEval,and it cannot know the specific content of the data. When the evaluation circuit consists of quantum gatesGi(i=1,...,N),the evaluated data is of the form

With regard toQCEvalcontaining theT-gate, the operations plotted in the previous section are performed by the server,including the CNOT operations, the definedUoperations and measurements. The operation on the non-maximally entangled state|Φ〉=m|00〉+n|11〉will be delayed to the decryption phase and carried out by the client. At last,the evaluated data is returned to the client.

Step 4In the final stage, the encryption keyekwill be updated as the decryption key by the client,where the decryption key is denoted asdk=(a′,b′). When the quantum gatesGi ∈Γ(Γ={X,Z,H,P,CNOT}) acting on the encrypted data,the key update rules are listed as follows:

d) WhenGi=CNOT, sinceCNOTis a two-qubit gate,both the control qubit and the target qubit require keys, that isek=(a,b,c,d)anddk=(a′,b′,c′,d′). Meanwhile,the encrypted state should be(XaZb ⊗XcZd)|φ〉. The corresponding key update rule is

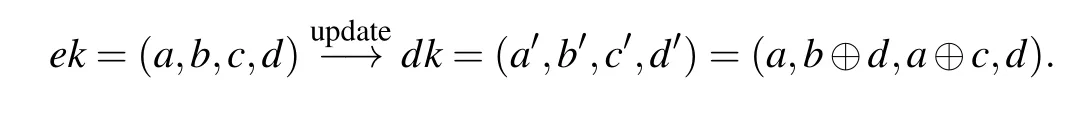
In the end, the evaluated data is decrypted using the decryption key to obtain the quantum circuitQCEvalthat performed on the original private data. It is a series of operations and computations that determined by the client in Step 1 in order to get the operated plaintext in private,since

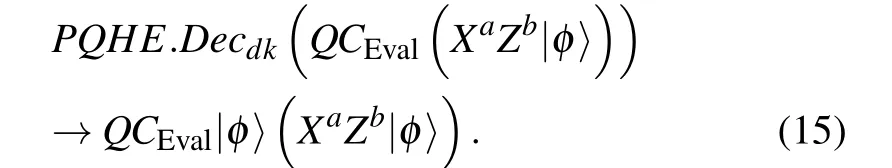
As introduced in the above scheme, we have made the novel two-party PQHE scheme come true. In the process of evaluating theT-gates,it can be seen from the expression(3)that whena=0, there is no error that needs to be corrected.In the case wherea=1,the evaluator has to correct the error.However, as we will see, the evaluator does not have access to the value ofaas theX-encryption key. The solution provided in our scheme is that the client and the server share the non-maximally entangled state in advance. The conditionalPcorrection needs to be delayed until decryption. The price we have to pay is that the value of the measurement result required to update the key can only be measured as part of the decryption algorithm. The proposal of the above scheme can not only correct the errors in the evaluation of theT-gates,but also ensure the correctness of the QHE scheme. At the same time,the security of the key can be guaranteed,which will not be obtained by the evaluator. Next,we will conduct a detailed security analysis of the proposed PQHE scheme.

4. Security analysis

In this section,we now analyze the security of our PQHE scheme in two ways,namely data and key.

Initially,for the original privacy data,only the client has access to them. Before transmitting this quantum information to the server, the client will use the QOTP technology to encrypt the privacy data|φ〉. The QOTP is an asymmetric quantum encryption method,which generates a pair of random keyek=(a,b)(a,b ∈{0,1})that is used only once.Therefore,the encrypted information becomes a totally mixed state, namely(1/2n)I.The expression(1)proves it clear. Even if an attacker may intercept the encrypted information and receive the complete quantum stateXaZb|φ〉during the transmission,the specific information still cannot be obtained.He has no idea about the value of the key, and the randomness of the key makes it irregular. The key is changed every time the information is encrypted. It will minimize the risk of information leakage, so the perfect security of privacy data is ensured.

Finally, the encryption keyekis a pair of classical bits(a,b) randomly generated by the client to carry out the key generation algorithm.Each pair of keys will be used only once in the encryption stage,making it impossible for the server to deduce the content of the key by studying regular pattern over time.At the same time,the decryption keydkis renewed from the secure encryption key by the key update rules. It is only consumed by the client. The key update rules are securely owned and applied by the client itself. The encryption keys and decryption keys will not be transmitted over the channel,so the server or other attackers will not be able to get any information about the keys. To conclude, it is obvious that the encryption and decryption keys have a perfect security.

In summary, through the above analysis, our PQHE scheme has good security performance on privacy data,evaluated data,encryption keys and decryption keys.

5. Conclusions

Quantum homomorphic encryption has affirmative advantages in protecting the privacy data,which can perform arbitrary quantum computation during the evaluation. And in the processing of encrypted quantum state,the privacy data is kept secret for the server. The focal point of computation is to correct errors in the evaluation of non-Clifford gate. When applied to a real communication scenario,under the influence of the noise in the outside environment,the maximum entangled state encountered obstacles in the preparation process. Hence,a novel two-party PQHE scheme is proposed. Our scheme shows that the non-maximally entangled state can be used as auxiliary resource to assist in the evaluation of universal quantum circuit. It ensures the security of private data and effectively implements the PQHE scheme. In a broader context,our work opens up a new possible way for the realization of QHE. Compared with the previous scheme, the technical requirements were relaxed in the preparation of quantum entangled states in our scheme. It lowers the requirements for quantum channel, so that our PQHE scheme is more likely to be implemented under the existing experimental conditions.

Firstly,the non-maximally entangled state was introduced when evaluatingT-gates to complete the correction of thePerrors in the evaluation stage. From an experimental viewpoint,we chose non-maximally entangled state to alleviate the stress on the quantum resources required in the scheme. And it indicated that the evaluation of the non-Clifford gates could be effectively implemented. Secondly,we constructed the specific two-party PQHE scheme described step by step through the explicit illustration. The homomorphic computation of universal quantum circuit on encrypted information was applied.The computations and operations were clarified that both the client and the server need to perform,and the access rights to the keys and data were determined respectively in the PQHE scheme.Finally,the scheme guaranteed the security of privacy data,evaluated data,encryption keys and decryption keys. In conclusion,our PQHE scheme attracts wide attention and may be an achievable QHE scheme, which is of practical importance for the realization of more sophisticated secure quantum computation and multiparty quantum communication.

We hope that the proposed scheme provides inspiration in speeding up the practical proceeding of QHE scheme and establishing the theoretical basis of information security in the context of quantum communication. Our results make contribution to the application of the theory of QHE in secure quantum computation, but the problem that remains open is the construction of the QFHE scheme. Therefore,it is one of our following researches to study how to combine the QHE scheme with other quantum and classical cryptography protocols to construct a QFHE scheme that has a more efficient performance.