Ab-initio investigation for the microscopic thermodynamics and kinetics of martensitic transformation

Tinle Wng ,Jinglin Du,＊＊ ,Shizhong Wei ,Feng Liu,b,＊

a State Key Laboratory of Solidification Processing,Northwestern Polytechnical University,Xi’an,Shaanxi,710072,China

b Analytical &Testing Center,Northwestern Polytechnical University,Xi’an,Shaanxi,710072,China

c National Joint Engineering Research Center for Abrasion Control and Molding of Metal Materials,Henan University of Science and Technology,Luoyang,Henan,471003,China

Keywords:Martensitic transformation First-principles Element effect Bogers-Burgers path

ABSTRACT Martensitic transformation(MT)path in Fe-based alloys remains uncertain in spite of decades of research.Lots of relevant works,which mostly focused on the simplest Bain path,have been completed by the state-of-the-art firstprinciples methods based on density functional theory.In this work,the element effects on microscopic thermodynamics and kinetics of the MT are investigated in terms of two different paths,including the well-known shear dominated Bogers-Burgers path and a recently proposed shuffle dominated path.Adding common elements,e.g.Ni,Mn,Cr,Si and C,into steel could induce different kinetics of the MT,as reflected by the energy barrier,which further determines the physically realistic MT path for different alloys.Furthermore,the addition of 3d transition metals may adjust the transformation equilibrium between the tetragonal α martensite and the hexagonal ε martensite,as reflected by their inverse effect on the energy barrier for the α MT and the stacking fault energy relating to the ε formation.An expected correlation between the thermodynamic driving force and the kinetic energy barrier for the MT is confirmed in binary Fe-Ni and Fe-Cr systems with changing the concentration of the alloying elements.These two paths for the MT are elaborately compared and discussed to reveal the nature of atomic movement in the MT,dominated by shear or shuffle.

1.Introduction

Martensitic transformation (MT) which occurs by cooperative movement of atoms over distances shorter than an atomic distance[1]is one of the critical phase transformations during the processing of steels.In the fascinating world of steel design the focus is mostly on the control of MT due to the significant role playing in the improvement of mechanical properties.Nowadays,to develop the advanced steels with the distinguished properties corresponding to a combination of high strength and high ductility,the major design mechanisms,e.g.transition induced plasticity describing a local MT of an austenitic phase,and the corresponding peculiarities of phase transformations involved should be understood at a more fundamental level to overcome the conventional trade-off relationship of strength-ductility.

Traditional thermodynamic investigation for MT aims at calculating the driving force (DF) to further obtain the parameter of MSor demonstrate the phase transformation mechanisms.In this regard,lots of thermodynamic models have been proposed [2-5],in which the DF is divided into chemical and non-chemical components.Although the chemical DF can be accurately obtained through CALPHAD approach[6],the indispensable experimental input endows the difficulty of it,due to the expensive sample preparation and the requirement of high precision measurements for obtaining sufficient experimental data.Moreover,some input,e.g.energetics of metastable or unstable phases,is missing due to the lack of corresponding samples.As for the non-chemical DF,several models have been proposed to calculate it [2,3,7],but with different treatments for energy terms,i.e.whether shearing energy,elastic energy and interfacial energy are included in the model or not,thus limiting their applicability under this non-unified plight.These models usually largely depend on the thermodynamic database,so any change of the database used will result in the change of coefficients in the model to give a different output than before [5].Although these thermodynamic models are physically reasonable the potential atomic movement or the crystallography of microscopic structural transformation is not particularly concerned,and thus the corresponding cognition is stagnated at phenomenological level.Thereupon,despite the extensive studies of the MT done over the past century,some questions,e.g.the actual atomistic behavior corresponding to a specific transformation modality,still remain unanswered or controversial,due to the complex microscopic nature and rapidity,which is even difficultly investigated by availably in situ experimental technologies limited by the resolution in space and time.

With the development of computational material science,firstprinciples calculations can provide insightful guidance for predicting energetics of phase transformations through a quantum mechanical description of the electronic structure[8,9],thus giving a very promising possibility to explore the microscopic thermo-kinetics of phase transformations to address the dilemma of excavating unknown atomic mechanisms.Compared with the traditional methods (i.e.experiment and theory),ab-initio method can be used to investigate the metastable phases which are difficultly studied in experiment,e.g.martensite,within a hitherto not achievable accuracy without adjustable parameters from experimental data.With the first-principles description for potential energy the thermodynamic DF and the kinetic energy barrier(EB)of MT can be obtained in the frame of the numerical algorithms for computing the minimum-energy paths (MEPs),e.g.the string method [10] and the nudged elastic band method [11-13].Following the transition state theory [1],the EB is mainly used for kinetic analysis,the magnitude of which can reflect the reaction rate of the MT.However,it is noteworthy that the computation of MEPs depends on the specific atomic displacements during MT in crystallography.Hence,the different crystallographic transition paths proposed for MT,e.g.the Bain distortion,the Kurdjumov-Sachs-Nishiyama shear/dilatation model and the Bogers&-Burgers(BB)model[14],may result in different DFs and EBs.

Unfortunately,previous ab-initio studies for MT are possible for highly idealized modalities only,such as the Bain transformation path[15-21]due to its simplicity in describing the structural transition from the face-centered cubic(fcc)to the body-centered cubic(bcc)transition at atomic scale,which corresponds to a distortion composed of a compression of 20%along the［001］fccaxis,accompanied by an expansion of 12%along the［110］fccand［110］fccaxes.As a refined version of the BB model,Bogers-Burgers-Olsen-Cohen (BBOC) model [22-25] was generally reported as the most probable displacement mode of atoms during the MT via experimental techniques [26-28] and molecular dynamics[29].While molecular dynamics is of importance in simulating atomic process of phase transformations,its applicability is limited by the deficiency of sufficient and reliable interatomic potentials for different Fe-based alloys,and therefore the previous focus is mainly on the system of pure iron.Furthermore,no relevant first-principles investigations have been reported until now to reveal the mechanism behind the BB or BBOC model.Although it is challenging due to the complex atomic process relative to the Bain path,a detailed investigation for the BB or BBOC path via first-principles calculations seems still inevitable to further deepen our understanding of the MT,because a simulation with high reference value should approximate the realistic situation as sufficient as possible.

Recently,a shuffle-dominated path for MT has been proposed by Zhang et al.[30,31] to explain the abnormal interstitial redistribution during the MT for the first time,in which the fcc →bcc transition can be accomplished through a specific Metastable Intermediate Structure(MIS),which is herein designated as MIS path.As such,whether the MT is shear-dominated or shuffle-dominated is still unclear to date.Moreover,it is naturally supposed that the additional elements should have different influences on the DF and EB of the MT path,which may result in the different transformation paths or mechanisms of atomic movement for different Fe-based alloys.The underlying reason can be attributed to the fact that different elements can induce different effects on the MT condition,as reflected by the stacking fault energy,mechanical property and magnetic state of austenite.Besides,a correlation between the DF and EB,as reported by Wang et al.based on the Bain path [15],may govern the formation of martensite.Hence,understanding the element effect on thermodynamics and kinetics of the MT path will benefit to reveal the microscopic mechanism of the MT in complex steel systems.

In this work,the DF and EB corresponding to the shear-dominated BB path and the shuffle-dominated MIS path are compared to reveal the real nature of atomic movement during the MT.Different alloying elements are separately added in pure iron to analyze the resulting variation of thermodynamics and kinetics of the MT.The atomic configurations and computational details are briefly introduced.And the calculated DF and EB are presented,along with the corresponding discussion on the atomic nature of the MT.

2.Methods and details

2.1.Atomic configurations

The BB path,proposed in 1964,is a“two shear”mechanism for the austenite (γ) →martensite (α) transition in steels,enjoying the great popularity since its birth [14,24].Based on the Bain correspondence Fig.1(a) shows that two homogeneous shears with the correspondingly dilatational component normal to the shear plane (i.e.two invariant plane strains)can provide the correct set of atomic displacements for the fcc →bcc transition.To unambiguously illustrate the“two shear”in the BB path,a specific shear plane and the corresponding direction are unified in this work,due to the multiple combinations of“two shear”in the same family of lattice planes.Starting from the primitive cell with six close-packed｛111｝γplanes in the fcc lattice,as denoted by the red lines in Fig.1(a),the first shear takes place on（111）γplane along ［112］γdirection over 1/18 aγ［112］γ.Except the green plane and its parallel plane in Fig.1(a),the other four｛111｝γplanes transform into the“70°-planes”of bcc,i.e.｛110｝α.We term this structure after the first shear as“one--shear-configuration”.The second shear,i.e.1/16 aγ［112］γslip on eachplane,then takes place to transform the remaining two planes holding invariable during the first shear into the“70°-planes”.As such,the correct stacking sequence for the bcc lattice generates via the BB path.In light of the coordinative movement of atoms during the two-shear process(i.e.each atom has the same surroundings due to the same displacement trajectory),a“one-atom”model is constructed to characterize the whole shear process,as shown in Fig.1(b),which can reproduce the essence of BB path illustrated above.

Although various mechanisms have been proposed to explain the experimental phenomena observed in the MT,some abnormal behaviors are still unclear in terms of the conventional shear picture of the MT,e.g.the abnormally low tetragonality of martensite.As a shuffle-dominated mechanism the MIS path can provide a new sight for this problem via describing the interplay between the redistribution of interstitials and the host lattice[30,31].Instead of a stable bulk phase,the MIS,serving as a connection between γ and α,is an interface structure,and therefore the MT proceeds along with a moving interface.Following the lattice correspondence among γ,MIS and α illustrated in Fig.2,one can see each of them has a tetragonal unit cell composed of 12 atoms,which are used for MIS path.Accordingly,the fcc →bcc transition can be accomplished by an atomic shear-like shuffle mechanism of adjacentlayers along the±［110］γdirections.In the MIS path,the fcc lattice will distort into a face-centered tetragonal(fct)structure of Fe by shear firstly,followed by the fct →MIS →bcc transition,which is mainly shuffle-dominated with minor change of cell shape.

2.2.Computational details

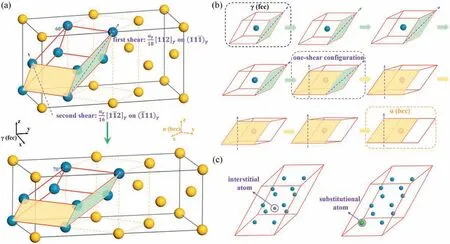
Fig.1.(a)Schematic diagram of MT via the BB path.The lattices up and down are separately fcc and bcc,where the orange dash lines show the Bain correspondence of the fcc →bcc transition.The parallel hexahedron denoted by red lines is the minimum unit cell for shear via the BB path.The green and yellow planes denote the first shear plane and the second shear plane,respectively;the corresponding shear directions are denoted by purple arrows.(b)The double-shear process of the“one-atom”model,which is used for constructing the atomic configurations for first-principles calculations.(c) The 2×2×3 supercell of fcc lattice obtained from the“one-atom”model,as a sample for illustrating the atomic configurations in multiple compositions,together with the labelled sites for substitutional atoms and interstitial atoms.

Fig.2.Atomic structures with respect to the MIS path.(a)the three-dimensional views of the tetragonal fcc lattice of pure iron,(b)the fcc lattice,(c)the MIS lattice and (d) the bcc lattice.The substitutional and interstitial atoms are represented by green large and gray small balls,respectively.

In this work,first-principles calculations based on spin-polarized density functional theory [32,33],as implemented in the Vienna ab initio simulation package (VASP) [34,35],were performed to optimize the atomic structures.The ion-electron interaction was described by the projector augmented plane-wave (PAW) method [36] and the X-C functional was described by an improved generalized gradient approximation (GGA) of Perdew-Burke-Ernzerhof (PBE) [37].The first-order Methfessel-Pack method [38] was used with a smearing width of 0.2 eV.A plane wave cutoff energy of 400 eV was used for all lattice optimizations.The Brillouin zone was sampled by Monkhorst-Pack scheme[39]with the k points per reciprocal atom over 10,000.In order to obtain the thermodynamic DF and the kinetic EB of the MT,the energy of atomic configurations along the transformation path should be calculated.For BB path,the configurations along the shear path,i.e.images,were created firstly via linear interpolation between the initial and the final structures,and then the corresponding energy was obtained by performing static calculation.For the MIS path,the corresponding minimum-energy paths,which can automatically capture the unknown configurations along the path,were searched using the generalized solid-state nudged elastic band(SSNEB)methods as implemented in the VTST code[11-13].SSNEB did not performed for the BB path,due to the determinative and known configurations along the shear path,which should not be relaxed and structurally adjusted in accordance with the atomic process specified by the BB theory itself.In order to approximate the magnetic condition for the MT that the fcc →bcc transition accompanied by the appearance of ferromagnetic order [8],we consider the structures in their ferromagnetic state for all calculations.The current work concerned with the ground state transition can provide a guidance for future investigations at finite temperatures.

As illustrated by Zhang et al.[31],there is no EB for the atomic rearrangement in the fcc →fct →MIS transition for the MIS path,thus only the MIS →bcc transition is considered in our computation to obtain the corresponding EB.The optimized lattice parameters of the MIS(a4.850 Å,b7.138 Å and c4.040 Å)and the martensite(a4.903 Å,b6.934 Å and c4.004 Å)of pure iron in Fig.2 are in good agreement with those reported by Zhang et al.In order to investigate the element effect on the thermodynamic DF and kinetic EB of the MT path,the Ni,Mn,Cr,Si and C are separately put into the atomic configuration of Fe for calculations.The corresponding solute concentration of the finally constructed atomic configuration is controlled via the size scale of the supercell of the host lattice with one solute atom.The“one-atom”structure of the BB path in Fig.1(b)is used to conveniently construct the supercells of Fe in multiple sizes by periodical expansion in 3D,including 2×2×3 (12 Fe atoms),1×2×7 (14 Fe atoms),2×2×4 (16 Fe atoms),2×3×3(18 Fe atoms)and 2×3×4(24 Fe atoms).The atomic configuration of the MIS path with 12 atoms can be treated following the similar philosophy.The sites of substitutional and interstitial atoms in Fe lattice for the BB path and the MIS path in calculations are shown in Figs.1(c)and Fig.2,respectively.

3.Results and discussion

3.1.Bogers-Burgers (BB) path

3.1.1.Element effect

To investigate the effects of element additions on thermodynamics and kinetics of the BB path,the common elements in steels,including Ni,Mn,Cr,Si and C,are selected to put into the supercells of Fe for firstprinciples calculations.Hereafter,we use“X" to represent the substitutional atoms.Accordingly,“FeNX”represents the alloy with X concentration of 1/(N+1)at.%,and the corresponding supercell is composed of N Fe atoms and 1 X atom.Fig.3 shows the energy evolution along the BB path for Fe,Fe11X,Fe23X,Fe12C and Fe24C alloy systems,wherein the DF is defined as the energy difference between the initial state and the final state,and the EB as the energy difference between the initial state and the transition state.Hence,the starting points of all the energy curves in Fig.3 are drew together for conveniently comparing the EBs of different alloy systems,although the energy values of the initial fcc lattices for different binary alloys are actually different.As expected,the transition state of the BB path appears in the first shear process(Fig.3),and there is no EB for the second shear process,as compatible with the characteristics of the BB path.This“one shear configuration”has a structure approximately midway between fcc and bcc,and can spontaneously be relaxed into bcc[24]by optimization of first-principles.Thus,it should be more appropriately described as a bcc-like structure without an accurate arrangement sequence of ｛110｝α,as reflected by the nonexistent EB in the second shear process.

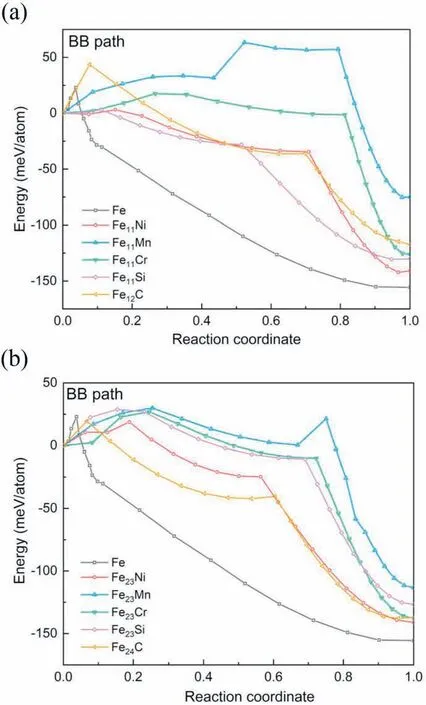
Fig.3.Calculated energy evolution during MT via the BB double-shear path from the initial fcc lattice to the final bcc lattice for(a)Fe11X systems and Fe12C,(b) Fe23X systems and Fe24C,where X Ni,Mn,Cr and Si.The middlemost image represents the obtained one-shear configuration after the first shear.

Obviously,the scattered curves in Fig.3 do reflect different effects of element additions on the BB path.Fig.3(a)shows that for alloys with the total solute concentration as 8.33 at.%,the additions of Ni,Cr and Si decrease the EB of the BB path relative to the pure Fe,and thus facilitates the fcc →bcc transition.This is in contrast with the inverse effect induced by the addition of Mn,which results in an abnormally large EB.As compared to Ni,Cr and Si,the addition of the interstitial C atom increases the EB.The result indicates that an important role of the relatively strong solid solution hardening effect of C plays in inhibiting the interface motion [40,41].Fig.3(b) shows the case of solute concentration decreasing to 4.17 at.%.Compared with the Fe11X and Fe12C the additions of Ni,Cr and Si will result in a larger EB for Fe23X systems.However,the additions of Mn and C will result in a smaller EB,which seemingly reflects the weakened element effect induced by the reduced concentration.Moreover,the EB of Fe23Cr and Fe23Si is larger than that of Fe,implying a restrain function for transition via the BB path;and the EB of Fe24C is smaller than that of Fe,implying a facilitated function,which are contrary to the element effects in Fig.3(a).Therefore,it is concluded that the element effects on the fcc →bcc transition should be associated with the concentration.

Element effects are also reflected in controlling the type of martensite transformation.The additions of 3d transition metals have considerable effects on the stacking fault energy of the fcc lattice,which plays a significant role in the development ideas of advanced high strength steels,e.g.the active deformation mechanism,twin-induced plasticity and transformation-induced plasticity [42].Apart from the α martensite in bcc,the ε martensite in hexagonal close packed(hcp)lattice also prevails in the alloys with low stacking fault energy.Given that both the stacking fault energy and the EB of the BB path are affected by the element additions,there should be a formation competition between the ε and α martensite.Using first-principles calculations,Limmer et al.found a parabolic-like behavior of the stacking fault energy of fcc iron across the period for 3d alloying elements [43],as shown by the trajectory of red dots in Fig.4.Except Mn,the additions of V,Cr,Co,Ni and Cu can increase the stacking fault energy,which further restrain the fcc →hcp transition.The underlying element effects on the stacking fault energy are correlated with the difference in the number of valence electrons of transition metals and Fe.Fig.4 shows the corresponding EBs of the BB path for Fe11X systems.As expected,the additions of V,Cr,Co,Ni and Cu except Mn decrease the EBs for α martensite formation,which is also related to the difference in the number of valence electrons of transition metals and Fe,i.e.the increased difference enhances the stacking fault energy but decreases the EB.Hence,the opposite effects of 3d elements on the stacking fault energy and EB do reveal a transformation equilibrium between the α and ε martensite,which deserves further investigations for benefiting the composition design of advanced steels.

3.1.2.Concentration effect

Taking Fe-Ni and Fe-Cr binary systems as typical examples,the effects of solute concentration of additional elements on thermodynamics and kinetics of the MT were studied.Fig.5 shows the calculated DF and the EB of the BB path for Fe11X,Fe13X,Fe15X,Fe17X and Fe23X.With increasing Ni concentration from 4.17 at.%(Fe23X)to 8.33 at.%(Fe11X),the DF decreases firstly and then increases,accompanied by a reverse variation of the EB.As for Fe-Cr system,the variation tendency of the DF is also contrary to the EB with increasing Cr concentration.Following the synergic variation of DF and EB,there may be a correlation between thermodynamics and kinetics.Although for any specific alloy system,the DF and the EB do not change monotonously at the whole concentration range,the trade-off relationship between DF and EB might exist at different local concentration ranges.This can be attributed to the electronic structure,the lattice strain degree and the binding among atoms etc.changing irregularly with the alloying content,so that the additions of common elements can lead to a parabolic-like relationship with the properties of alloys [44,45],e.g.strength and stacking fault energy,which further determines the EB of MT,leading to the non-monotonous variation of EB with multiple extremums along the concentration axis.

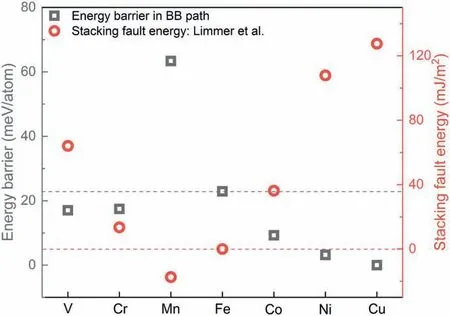
Fig.4.Calculated energy barriers of the BB path for Fe11X systems with XV,Cr,Mn,Fe,Co,Ni and Cu as the 3d transition metals,together with the stacking fault energy of the fcc lattice reported by Limmer et al.[43]after the addition of 3d transition metals to pure iron.

Such correlation between thermodynamics and kinetics,as reported by Wang et al.[15],where the trade-off relationship between DF and EB of the Bain path is demonstrated to be correlated with the finite temperature,is concluded to be also related to the concentration via the BB path.Bos et al.found a linear proportional relationship between DF and the velocity of interface motion for MT by molecular dynamics [46].As such,if the addition of typical alloying atoms reduces the interface velocity,as represented by the increased EB and the decreased DF,thus the correlation between DF and EB is naturally established,which should be ubiquitous with the variation of phase transformation conditions,e.g.temperature and composition.Understanding this potential correlation can provide a new insight for the microscopic mechanism of MT.

3.2.Metastable Intermediate Structure (MIS) path

Fig.6 shows the DF and EB of the MIS →bcc transition in MIS path for Fe11X and Fe23X systems.The additions of Ni,Cr and Si can also decrease the EB of the MIS path for alloys with solute concentration of 8.33 at.%,as shown in Fig.6(a).This is analogous to Fig.3(a) for the BB path.However,contrary to the BB path,the EB of Fe12C is larger than that of Fe11Mn in the MIS,showing the strong interaction between the interstitial atoms and the host atoms during the shuffle process.With the decreasing of the solute concentration value from 8.33 at.% to 4.17 at.%,the energy curves of Fe23Ni,Fe23Cr,Fe23Si and Fe24C,except Fe23Mn,move toward the curve of Fe,resulting in the centralized curve cluster,as shown in Fig.6(b).This implies a more obviously weakened effect due to the reduced solute concentration for the MIS path,as compared to Fig.3(a) and (b) for the BB path.The Fe-Mn alloys always have the largest EB for the MIS path in Fe-X systems,indicating the restrain effect of Mn on the α MT,as illustrated in Section 3.1.1.Most importantly,the effects of element additions on the MT,either facilitated or restrained,remains unchanged in terms of the EB for the MIS path between Fe11X and Fe23X systems.

3.3.Nature of martensitic transformation path

To doubtlessly reveal the nature of the MT the atomistic calculations should approach the realistic process of phase transformation as adequately as possible.However,the application of first-principles calculations is usually limited by the complex characteristics in steels,e.g.the finite temperature and magnetism,thus the realistic process seems difficult to be directly considered.Traditional phenomenological theories,although lacking the elaborate physical mechanisms at atomic level to some extent,can serve as the medium between the first-principles and the realistic process,since its power of reflecting the experimental phenomena with several adjustable parameters.As such,when the results of atomistic calculations are linked to the phenomenological theories,the reality of MT can be indirectly linked.

In principle,the EB obtained by first-principles calculations should be correlated with the properties of the MT in traditional phenomenological kinetic theories,particularly the nucleation model proposed by Ghosh and Olson [2,3,47].In their nucleation model,the interfacial frictional work wμis a composition dependent parameter:

where the scale coefficient Aμand the isotropic shear modulus μγare given as:

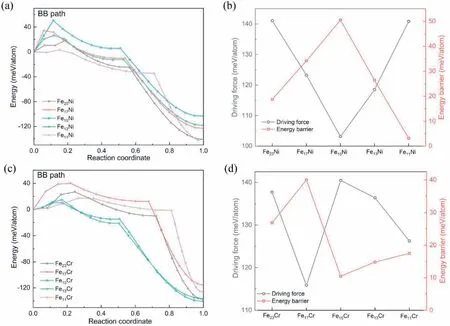
Fig.5.Calculated energy evolution during MT via the BB double-shear path from the initial fcc lattice to the final bcc lattice for (a)Fe-Ni alloy system with (b) the corresponding variation of the DF and EB,and (c) Fe-Cr alloy system with (d) the corresponding variation of the DF and EB.The middlemost images in (a) and (c)represent the obtained one-shear configurations after the first shear.

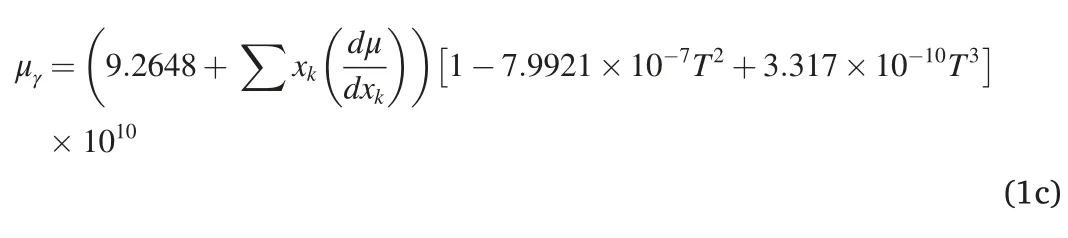
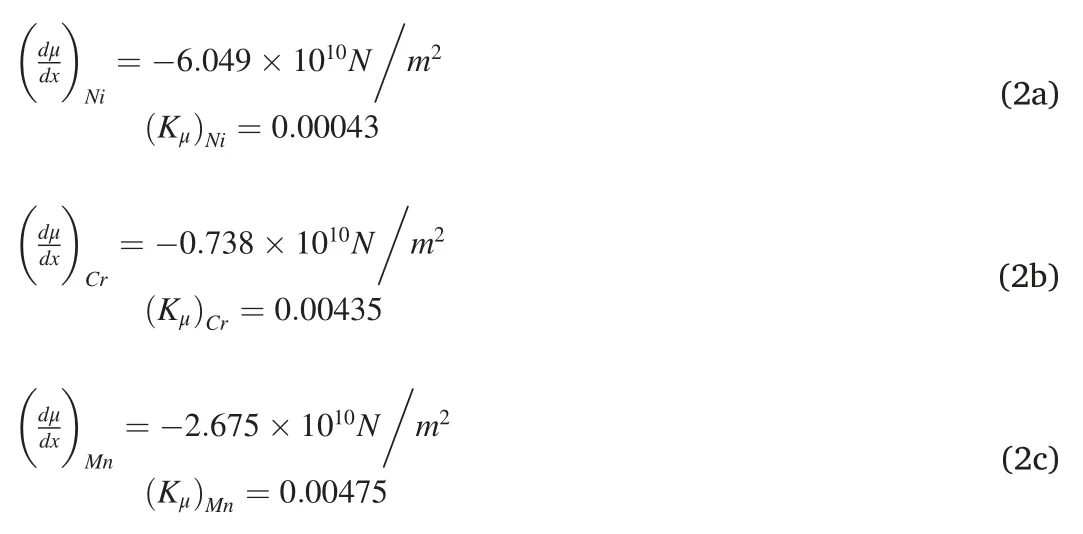
Taking Fe11X and Fe12C as examples,their corresponding interfacial frictional work values of wμare calculated based on Eq.1(a-c) and Eq.2(a-e).The obtained values of wμ(×107J/m3)for different elements are as follows,(wμ)C(23.66) ＞(wμ)Mn(12.37) ＞(wμ)Cr(11.53) ＞(wμ)Si(8.926) ＞(wμ)Ni(1.086),showing an analogous sequence with the variation of EB for the MT,i.e.EBC＞EBMn＞EBCr＞EBSi≈EBNiin the MIS path.Hence,it can be deduced that,on the one hand,a correlation between the EB of the MT and the interfacial frictional work should exist,since both of them are regularly influenced by the alloying elements;On the other hand,the realistic probability of the existence of this revolutionary shuffle dominated MIS path for the MT is ensured by this way.In the present work,effects of the finite temperature and the magnetism are not meticulously considered,which will be included in the future work to further clearly declare the link between the atomic scale computation and the traditional phenomenological theory.

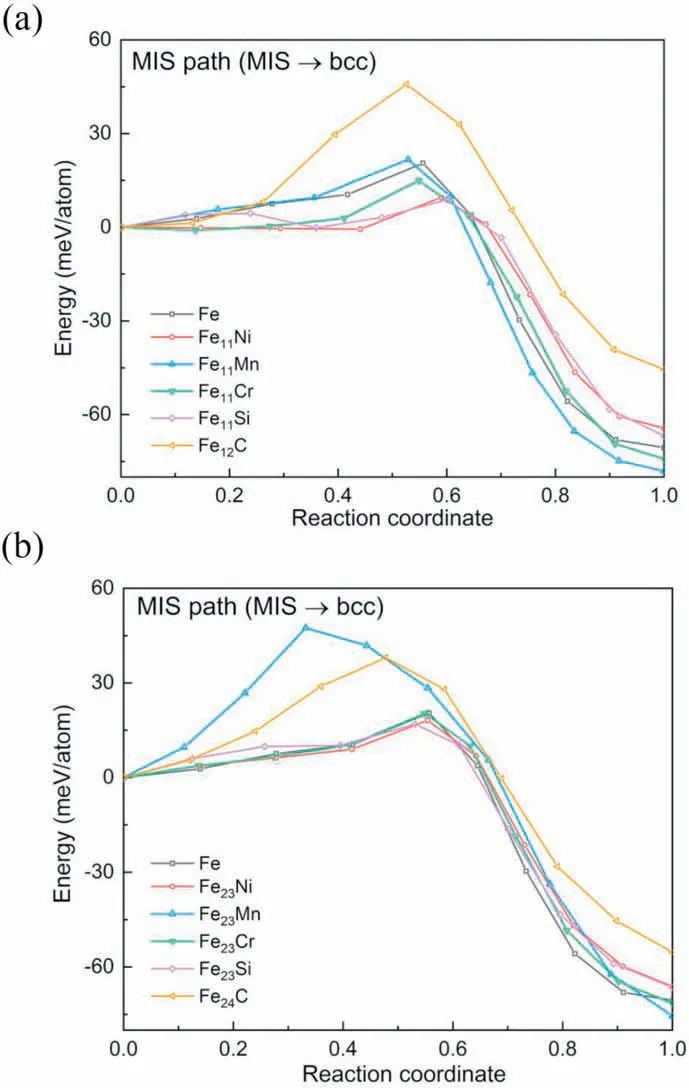
Fig.6.Calculated energy evolution during MT via the MIS path from the MIS to the bcc lattice for (a) Fe11X systems and Fe12C,(b) Fe23X systems and Fe24C,where X Ni,Mn,Cr and Si.Note that the fcc →fct →MIS transition is not presented,because the EB only exists in the MIS →bcc transition process.

Whether the MT should conform to the shear-dominated BB path or the shuffle-dominated MIS path can be preliminarily revealed.Table 1 lists values of the DF and EB corresponding to the element effects on the shear-dominated BB path and the shuffle-dominated MIS path.Although the conventional shear path inducing a large elastic strain seems inferior to the MIS path involving minor shape change of cell,the EBs for both paths involved in the fcc →bcc transition are of the same order of magnitude.For different alloys,the preferential path can be chosen between the BB path and the MIS path by comparing their EBs.With changing the solute concentration,the preferential path can change,implying the coexistence of these two paths in a single bulk material due to the actually inhomogeneous distribution of alloying atoms in the matrix at the microscale.It then follows that,the combination of shear and atomic shuffle mechanisms provides a more comprehensive explanation for the experimental phenomena of the MT.For examples,the shear dominated path endows certain characteristics of the MT,including the habit plane,the orientation relationship and the shape deformation etc.[1],while the MIS path is responsible for the observed tetragonality of martensite [31].As such,the experimental phenomena observed for the MT can be self-consistently understood via our predicted synergy of the BB or the BBOC path and the MIS path.Although only binary Fe-based alloys are considered in the current work,the atomic mechanisms of MT should be ubiquitous,no matter in simple or complex steels,due to the same atomic characteristic existing in both cases that MT proceeds mainly via the movement of host Fe atoms.Anyway,with the development of computational hardware and the better theories for describing the interaction of atoms,this microscopic thermo-kinetic investigation is promisingly expanded to the complex steel systems to provide a direct reveal of the path of MT.

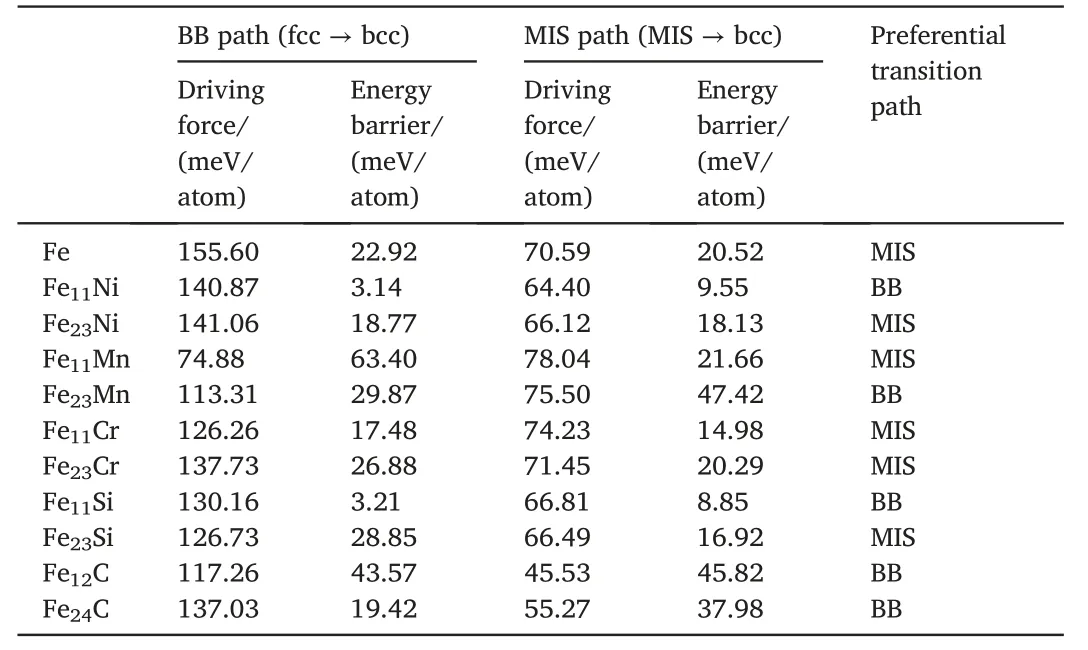
Table 1 Calculated driving force and energy barrier in the BB path and the MIS path for the MT of different alloy systems,including binary Fe-Ni,Fe-Mn,Fe-Cr,Fe-Si and Fe-C systems.

4.Conclusion

Microscopic thermodynamics and kinetics of the shear dominated BB path and the shuffle dominated MIS path for the MT are investigated by performing first-principles calculations.The effect of element additions on the EB of the MT path,i.e.either facilitated or restrained for the fcc →bcc transition,changes with the concentration.It is demonstrated that the 3d transition metals have opposite effects on the EB of the MT and the stacking fault energy,thus affecting the transformation equilibrium between the α martensite and the ε martensite.Following the variation of EB and DF of the BB path with the solute concentration of Fe-Ni and Fe-Cr systems,a correlation between thermodynamic DF and kinetic EB,which can govern the MT in steels,is confirmed.The values of the EB for the MIS path and the BB path are the same order of magnitude,thus the realistic MT may proceed in the manner of the coexistence of the BB path and the MIS path.The preferential path can be chosen based on the composition of the local microscopic area.The synergy of the traditional shear model and the shuffle model can self-consistently explain the common phenomena observed experimentally for the MT.Further investigations along this direction,e.g.the calculations with the consideration of finite temperature and magnetism,are still required to assist our understanding of underlying mechanism behind the MT and developing the newly advanced steels.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

The authors are grateful for the financial support from the National Key R&D Program of China(Nos.2017YFB0703001,2017YFB0305100),the Natural Science Foundation of China (Nos.51134011,51431008),the Research Fund of the State Key Laboratory of Solidification Processing (Nos.2019-TZ-01,2019-BJ-02),the China Postdoctoral Science Foundation (Nos.2018M643729,2019T120942),and the Natural Science Basic Research Plan in Shaanxi Province of China (No.2019JQ-091).