基于数值天气预报后处理的参考作物蒸散量预报改进
姚付启 董建华 范军亮 曾文治 吴立峰
(1.鲁东大学水利工程学院, 烟台 264010; 2.南昌工程学院水利与生态工程学院, 南昌 330099;3.西北农林科技大学水利与建筑工程学院, 陕西杨凌 712100;4.武汉大学水资源与水电工程科学国家重点实验室, 武汉 430072)
0 引言
准确的蒸散量预报对作物需水量、驱动水文和作物生长模型评估以及农业和水资源管理决策具有重要意义。蒸散量可以通过蒸渗仪、涡动相关和波文比等系统观测,但这些设备通常价格昂贵,且维护成本很高[1]。作物的实际蒸散量更多采用参考作物蒸散量(ET0)函数进行推导[2]。
Penman-Monteith方程(以下简称FAO56 PM)[3]是国际公认的计算ET0的标准方法。FAO56 PM方程是一种基于物理的方法,结合了生理和空气动力学参数[2],并不需要参数本地化校正。然而,FAO56 PM方程要求太阳辐射、气温、风速和相对湿度等气象资料齐全。
近年来,学者们不断尝试使用公共天气预报信息进行未来ET0的预测。CAI等[4]将公共天气预报的多云情况、每日最高和最低温度以及风速等级转换为FAO56 PM公式所需的信息,获得了理想的ET0预报精度。LUO等[5]使用1~7 d公共天气预报和Hargreaves-Samani模型进行ET0预报,其均方根误差(RMSE)介于0.87~1.36 mm/d,相关系数介于0.64~0.86。CHANG等[6]使用改用Thornthwaite模型基于公共天气预报的气温数据对ET0进行了预报。YANG等[7]研究发现,天气预报风速对ET0估算精度低于多年的日平均风速。
进入21世纪以来,数值天气预报(Numerical weather prediction,NWP)模型在高空探测影响天气过程、气候变化和全球尺度天气异常方面取得了巨大的进展[8]。如同基于卫星和雷达观测的数据同化技术[9-10],NWP的进步是计算机能力增强、模型的时空高分辨率以及预报技术和工具改进的直接结果。NWP基于流体动力学方程通过确定性或概率的方法来描述大气运动,需要明确的边界条件。初始条件的偏差、方程的简化或某些因素的低预测性都可能造成天气预报失灵。因此,预报的结果需要对逐个变量和逐个站点进行检查。通常使用地面气象站点数据对NWP的网格值进行偏差校正或后处理[11]。MEDINA等[12]采用欧洲中尺度天气预报系统(EC)、英国气象局预报系统(BMO)和美国全球集合预报系统(GEFS)集合预报的方法来改进单个NWP模型预报能力的不足。
机器学习算法由于具有极强的非线性拟合能力,已被应用于气象数据的空间校正、ET0预测预报等领域。LUO等[13]将ANN和天气预报相结合,预测我国不同地区的ET0。YIN等[14]评估了4种神经网络方法在预报ET0中的表现,发现多层感知器的效果最好。TRAORE等[15]使用双向长短记忆神经网络对ET0进行了7 d预报。LU等[16]使用蝙蝠算法耦合XGBoost对未来1~3个月的ET0进行了预测。
目前,基于NWP对ET0预报的预报期多为7 d以内,从灌溉决策的角度,迫切需要预报期为15 d以上的可靠方法。以往研究多为基于单气象要素的偏差校正,但NWP输出气象因子的预报结果与相应观测值是否匹配尚不明确,其他预报因子是否蕴藏着提高ET0预报性能的重要信息等相关研究还未见报道。因此,本研究以第二代全球集合预报系统在我国西北地区的输出产品为例,以1~16 d为预报期,基于LightGBM机器学习模型,检验NWP气象预报因子与相应观测值的匹配程度,探索使用多输出结果提高单个气象要素预报精度的可能性,以提高ET0的预报能力。
1 材料与方法
1.1 研究区域概况
西北干旱区位于中国内陆西北部,属大陆性内陆气候区。气候干燥,年降水量主要分布在200~400 mm,水资源比较紧缺。天然植被的分布以典型干草原、荒漠草原、荒漠为主。年平均气温5~10℃。四季分明,昼夜温差大,全年日照达3 000 h,无霜期170 d左右,是全国太阳辐射资源最充足的地区之一,特别适宜农作物及瓜果生长。
1.2 数据来源
本研究数据来源有2个,其中气象站点数据来自中国气象数据共享网(http:∥www.cma.cn),选取了中国西北地区9个站点(图1)作为研究对象,气象数据包括:每日2 m高处最高和最低气温(Tmax和Tmin)、地表总辐射(Rs)、相对湿度(RH)和2 m高处风速(U2)(表1)。数值天气预报数据来自NOAA的第二代全球集合预报系统(GEFSv2)[17],1~8 d和9~16 d的空间分辨率分别为0.5°×0.5°和1°×1°。数据包括未来1~16 d的2 m最高和最低气温、向下短波辐射、比湿度、U和V方向风速,时间分辨率为4 h和6 h,其中比湿度转换为相对湿度,U和V方向风速经加权平均获得平均风速。2个数据集数据分为2部分, 2005—2014年用于模型建模(训练),2015—2019年用于检验模型。

表1 本研究所选气象站点概况
1.3 研究方法
1.3.1反距离权重法
反距离权重(IDW)法基于两个假设:未知值附近的点影响比远的控制点影响更大;影响程度(权重)与彼此之间的距离的倒数成指数关系[18],其计算式为
(1)
式中Z——被插值点的值
zi——控制点的值
本研究使用气象站点周围NWP的4个控制点信息并使用IDW法进行插值。
1.3.2等距累积分布函数法
累积分布函数匹配(CDFm)方法[19]是一种广泛应用的偏差校正方法,它需要假设模型和观测数据的累积分布一致。为了克服这一问题,LI等[20]提出了等距累积分布函数匹配(EDCDFm)法,该方法对模型和观测的累积分布曲线进行了偏差的校正。EDCDFm定义为
(2)
式中F——累积频率函数
F-1——累积频率函数的反函数
Xm′——校正后的未来模型预测值
Xm——数值天气预报的未来模型预测值
下角o表示历史训练期观测值,s表示历史训练期模拟值,s′表示未来模型模拟值。
本研究中,首先使用IDW方法将NWP数据插值到气象站点,然后使用3次函数对气象因子的累积频率曲线进行拟合。
1.3.3LightGBM法
LightGBM是传统GBDT的一种高效改进算法,擅长处理高维数据,能提高计算效率,同时保证高模型精度[21]。传统的决策树算法采用层次策略对树进行生长,对同一层的叶子不加区分地进行处理,造成了不必要的计算成本(图2)。为了降低训练数据的维数,该算法的决策树采用叶向生长策略。每一次从所有的叶子中,找到一个最大的分裂增益,然后分裂完成一个循环[22]。为了避免在样本量不足时过拟合,有必要增加树的最大深度限制。LightGBM还可以使用Gini得分对输入特征的重要性进行排序,在建模时剔除干扰因子。本研究中,LightGBM分别基于两种方式进行建模(表2),第1种为使用单因子对单因子的方式对气象因子进行偏差校正,记为M2方法,该方法每个站点训练样本数为4×3 652=14 608个,检验样本数为4×1 826=7 304个;第2种同时使用5个气象因子依次对其中一个气象因子进行偏差校正,记为M3方法。使用预报期1~16 d分别作为输入,观测值作为输出来建立模型,M2方法的输入特征数量是4站点×6个时刻(第4天开始4个时刻),共24(16)个,M3方法的输入特征数量是4站点×6个时刻(第4天开始4个时刻)×5要素,共120(80)个。本研究中所需要调参的参数有:最大树深度、学习率和树的个数,调参使用网格搜索法[23]。
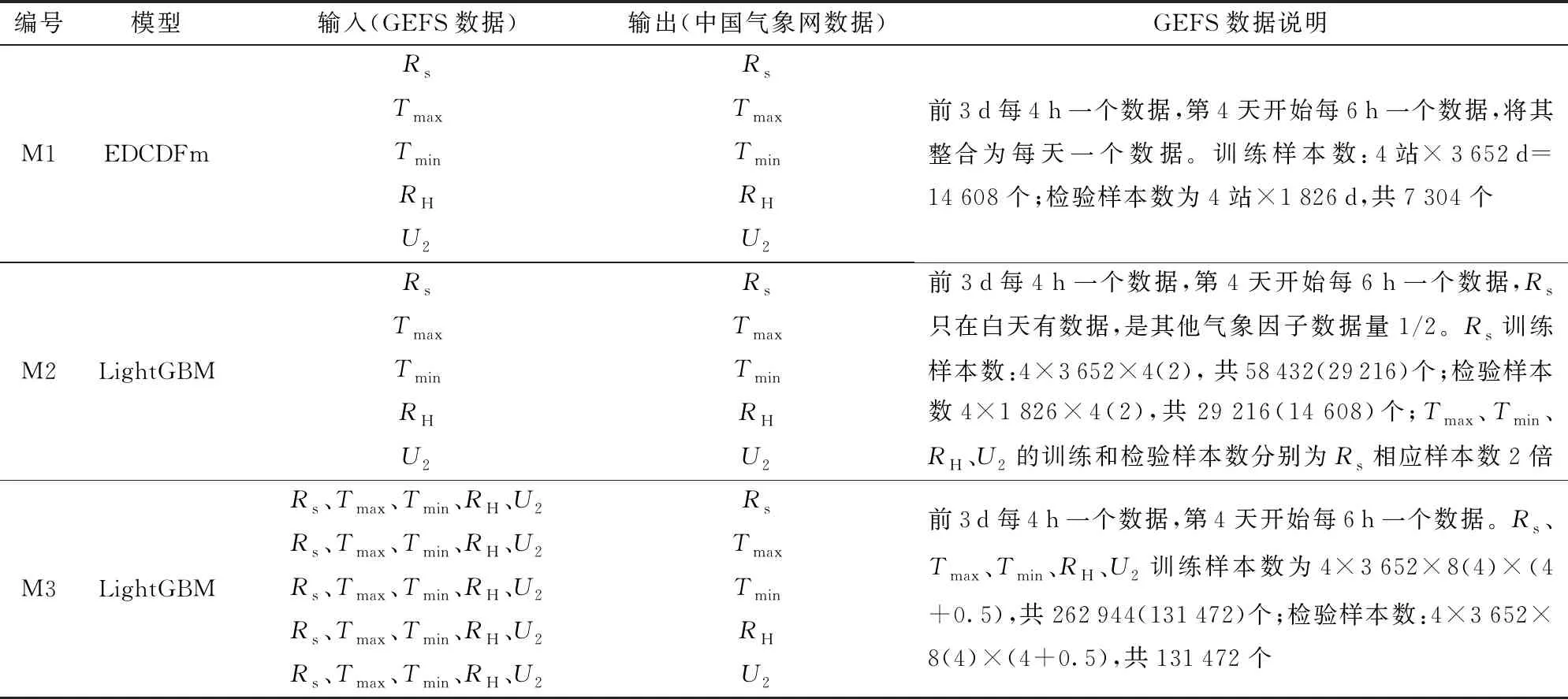
表2 本研究所使用偏差校正方法
1.4 FAO-56 Penman-Monteith 模型
采用FAO-56 PM法[23]计算西北地区9个站点的ET0,计算公式为
(3)
式中ET0——参考作物蒸散量,mm/d
Rn——地表净辐射,MJ/(m2·d)
G——土壤热通量密度,MJ/(m2·d)
Tmean——2 m高处的平均气温,℃
es、ea——饱和与实际水汽压,kPa
Δ——蒸汽压曲线的斜率,kPa/℃
γ——温度计常数,kPa/℃
1.5 评估指标
采用均方根误差(RMSE)、决定系数(R2)和平均绝对误差(MAE)来评估气象因子误差。
2 结果与分析
2.1 气象因子预报精度比较
2.1.1气温
气温是影响饱和水汽压和地面长波辐射收支的重要因子,从而间接影响了ET0的变化。3种方法在未来16 d的Tmax预报精度如图3a~3c所示。随着预报天数的增加,Tmax的预报精度呈下降趋势。M1、M2和M3方法在9站点平均RMSE介于2.57~5.03℃、2.31~4.82℃和2.01~4.36℃,MAE介于1.90~3.89℃、1.71~3.75℃和1.48~3.40℃;R2介于0.87~0.97、0.87~0.97和0.89~0.98。由此可以看出,3种方法的精度由高到低依次是M3、M2和M1。
Tmin的预报精度也随预报期的延长而下降(图3d~3f),但总体上误差小于Tmax,其M1、M2和M3方法在9站点平均RMSE介于 2.11~4.03℃、2.65~4.10℃和2.26~3.76℃,MAE介于1.90~3.41℃、2.28~3.39℃和1.94~3.06℃,R2介于0.88~0.97、0.87~0.95和0.90~0.96。尽管M1方法在站点6、9等表现优于M2方法,但是在站点1、2、3精度明显低于M2方法,特别是在预报期9~16 d精度较差。总体上,M3方法优于M1和M2方法,其在预报期前8 d精度稍高于M1方法,但是9~16 d明显优于M1方法。
2.1.2地表总辐射
辐射是蒸散的最主要能量来源,其直接主导地表气温变化。3种方法在不同站点预报Rs的表现如图3g~3i所示。3种方法在预报Rs的前8 d精度逐渐下降,在第9天开始由于网格尺度变大造成了Rs明显下降,其后精度又逐渐下降。其中,M1、M2和M3方法在9站点平均RMSE介于3.44~5.23 MJ/(m2·d)、3.53~5.22 MJ/(m2·d)和3.22~4.91 MJ/(m2·d),MAE介于2.52~3.76 MJ/(m2·d)、2.57~3.83 MJ/(m2·d)和2.37~3.64 MJ/(m2·d),R2介于0.82~0.59、0.81~0.57和0.85~0.61(从前期到后期)。总体上,M3方法表现优于M1和M2方法,而M1和M2方法误差比较接近。此外,3种方法在站点1、2、9的误差较大,特别是9~16 d,RMSE超过了5 MJ/(m2·d),R2也在0.5以下。
2.1.3风速
风速是影响空气阻力的重要因子。3种方法在不同站点预报U2表现如图3j~3l所示。3种方法在预报U2不同站点呈现明显差异。在站点2、3、6、7,3种方法在预报期1~16 d都呈现较好的表现。而在站点4总体表现较差。其他站点前8 d比后8 d的精度高50%以上。其中,M1、M2和M3方法在9个站点平均RMSE介于0.67~0.87 m/s、0.53~0.69 m/s和0.49~0.64 m/s,MAE介于0.48~0.62 m/s、0.39~0.51 m/s和0.36~0.47 m/s,R2介于0.03~0.24、0.04~0.37和0.10~0.43。
2.1.4相对湿度
相对湿度(RH)是估算饱和水汽压亏缺的重要因子。3种方法在不同站点预报RH表现如图3m~3o所示。3种方法在预报RH的前8 d精度快速下降,在第9天开始由于网格尺度变大造成了精度急剧下降,部分站点的精度已经接近随机分布,可以看出GEFSv2总体上预报RH的能力比较一般。其中,M1、M2和M3方法在9站点平均RMSE介于15.0%~17.2%、11.7%~14.4%和10.0%~13.1%,MAE介于12.0%~13.5%、9.0%~11.4%和7.6%~10.2%,R2介于0.19~0.42、0.25~0.53和0.36~0.66。可以看出,M3方法优于M2和M1方法,而M2方法优于M1方法。
2.2 ET0预报精度比较
3种方法在不同站点预报ET0表现如图3p~3r所示。3种方法在预报ET0误差随预报期延长呈上升趋势,其中,M1、M2和M3方法在9站点平均RMSE介于0.66~0.93 mm/d、0.57~0.83 mm/d和0.53~0.79 mm/d,MAE介于0.44~0.61 mm/d、0.38~0.56 mm/d和0.35~0.53 mm/d,R2介于0.82~0.91、0.84~0.93和0.86~0.94。可以看出,3种方法的精度从高到低依次是M3、M2和M1。从站点看,站点3、7的精度最高,1~16 d的误差都没有超过0.8 mm/d,而站点4、9的误差较大,特别是9~16 d,其RMSE已经超过了1 mm/d。
3种方法在站点5不同预报时段FAO56 PM估算值与预报值的散点图如图4所示。M1方法在预报期1~16 d的R2从0.91下降到0.82,从第4天起存在着严重的高估问题,特别是PM 估算值大于3 mm/d时,有大量点预报值达到了8 mm/d以上。M2方法在预报期1~16 d的R2从0.92下降到0.84,与M1方法相比,散点更接近于1∶1线附近,在PM估算值大于8 mm/d时,存在一定的低估问题。M3方法在预报期1~16 d的R2从0.93下降到0.85,与M1和M2方法相比,其散点更接近于1∶1线附近,且在预报期1 d提升最明显,此后提升效果逐渐减弱。
从农业灌溉角度出发,一个灌溉周期连续多日的平均误差比单日误差更适宜为灌溉决策提供参考,因此,计算了1~8 d和1~16 d 3种方法的统计指标,并列出了未进行偏差校正(仅使用IDW方法)的统计指标作为对照,其结果如表3所示。从表3可以看出,IDW方法下只有站点2、3的RMSE在1 mm/d以内,说明该数据集整体误差很大难以直接使用,需要偏差校正。对比以上4种方法统计指标可以看出,M1、M2、M3 3种方法均可以大幅度降低模型的预报误差。与IDW方法相比,M1、M2和M3方法的RMSE在9个站点1~8 d分别下降26%~65%、24%~70%和31%~73%,在9~16 d分别下降20%~63%、20%~68%和24~70%。尽管M3方法相比M1方法在1~8 d和1~16 d分别有13%和15%的提升,但是两者RMSE的绝对误差在0.15 mm/d以内。从全年角度来看可能并没有明显的优势。因此,有必要评估不同方法在不同季节,特别是灌溉季节的表现。

表3 不同方法下ET0在1~8 d和1~16 d累计误差
2.3 ET0预报季节差异
3种方法在不同季节的RMSE如图5所示。在春季,M1、M2和M3方法的1~16 d平均RMSE为0.89、0.90、0.80 mm/d。3种方法的RMSE随预报期的延长呈增加趋势,其中M1方法的RMSE从0.74 mm/d增加到1.03 mm/d,M2方法从0.86 mm/d缓慢增加到0.94 mm/d,M3方法的RMSE在前8 d从0.61 mm/d快速增加到0.83 mm/d,之后增速逐渐放缓,在16 d达到0.9 mm/d。对比M1和M2方法可以看出,在前8 d,M1方法表现优于M2方法,而在后8 d,M2方法优于M1方法。
在夏季,3种方法的表现与春季相似,1~16 d平均RMSE为1.21、1.18、1.04 mm/d。不同之处在于由于夏季ET0比春季更高,因此夏季的误差更大。M1方法的RMSE在0.98~1.4 mm/d,而M2和M3方法可以把最大误差控制在1.2 mm/d附近。此外,在前6 d,M1方法表现优于M2方法,而在6 d以后M2方法优于M1方法。秋季和冬季呈现与春季和夏季相似的趋势。M3方法在预报初期优于其余2种方法,但随着预报期增长,其优势逐渐变小,在8 d以后,3种方法的RMSE相差约在0.1 mm/d。
2.4 气象因子对误差的影响
为了发现NWP系统的不足之处,进一步评估了单个气象因子的预报误差对ET0预报精度的影响。使用M3方法并分别使用1种预报数据与其余4种观测数据组合代入PM公式,来评估气象因子预报误差对ET0误差的影响,结果见图6。从图6a、6b可以看出,最高和最低气温的误差对ET0误差的影响在不同季节有所差异,由大到小为春季、夏季、秋季、冬季。此外,Tmax预报误差对ET0造成的误差比Tmin大。在夏季,Rs的误差对ET0影响更大,ET0的RMSE在1~16 d介于0.55~0.83 mm/d(图6c),与前文相比,其误差已经达到了总误差的70%以上。而春季,由于Rs预报误差导致ET0的最大RMSE仅为0.42 mm/d。U2预报误差对ET0影响在春季和夏季相差不大,其ET0的最大RMSE约为0.4 mm/d,秋季则高于冬季(图6d)。RH预报误差对ET0影响较小,在夏季与春季相差不大,其ET0的最大RMSE约为0.2 mm/d(图6e)。对比不同气象因子造成的影响可以看出,Rs对ET0误差贡献最大,其后依次是U2、Tmax、RH和Tmin。从2.1节可以看出,各气象因子中预报误差最大的是U2,其后依次是RH、Rs、Tmax和Tmin。由于不同因子对ET0的贡献度不同,造成了其自身预报误差与对ET0的误差贡献有所不同。尽管U2的误差最大,但由于其对ET0影响较小,因此对ET0误差影响仅排在第2位,而Rs尽管预报精度排第3,但由于其对ET0贡献最大,因此其对ET0误差的贡献也最大。这表明提高Rs的预报精度是更准确预报ET0的关键。
2.5 预报气象因子与观测气象因子之间关系
为更好地认识数值天气预报系统气象因子内在的联系,基于LightGBM模型对气象因子进行偏差校正基础上,通过算法对因子贡献度评分(Gini值)绘制预报气象因子之间的相关关系图,其各输入因子对输出气象因子的得分结果如图7所示。可以看出,GEFS_Tmax信息对于提升Tmax、Tmin、RH和U2的预报精度都有较大的帮助。GEFS_Tmax的Gini值为2.1,其中仅有约0.9的得分用于预报Tmax,约0.6的得分用于预报Tmin,甚至高于GEFS_Tmin对Tmin的预报得分(0.25),这说明与Tmin变化规律最接近的是GEFS_Tmax,而非GEFS_Tmin。
GEFS_Rs除主要用于预报Rs外,对RH和U2的预报稍有帮助。此外,GEFS_RH对RH预报得分只有0.2,而GEFS_Tmax对RH预报得分为0.45,高于前者。这说明使用GEFS_Tmax来预报RH比GEFS的GEFS_RH预报更有效。综合来看,Tmax对其他因子预报的贡献最大,其后依次是Rs、Tmin、U2和RH。另一方面,多因子预报对太阳辐射预报的帮助最小。以上信息说明,预报因子与观测气象因子之间存在不匹配的问题,不匹配程度与因子有关,其中Rs的匹配度最高,RH匹配度最低。这也证明了本研究使用多因子偏差校正的合理性。
3 讨论
目前,ET0预报主要基于公共天气预报和数值天气预报。公共天气预报容易获得、只需要简单转换就可以使用,跟经验模型结合更能简化计算流程[24],但由于数据的完整度存在问题,公共天气预报的预报期通常较短,多为7 d以内[5-7,25-26]。数值天气预报具有更完整的数据集,且预报期更长,通常可以预报10 d以上,甚至1个月。但数值天气预报通常前处理比较复杂,并且需要偏差校正,这给其广泛使用带来了一定的困难,在NWP基础上进行后处理,构建预报数据集有助于简化其复杂度。YANG等[7]比较了不同4种风速输入方式在中国不同气候区ET0预报的表现,其中在干旱区RMSE介于0.95~0.99 mm/d,MAE介于0.67~0.70 mm/d。本研究中,M3方法在9站点1~16 d平均RMSE介于0.53~0.79 mm/d,MAE介于0.35~0.53 mm/d,说明NWP结合后处理方法比公共天气预报的精度更高。此外,本研究结果还证明了机器学习方法比统计方法精度更高,在相同输入条件下,M2方法比M1方法RMSE低12.0%~15.7%,MAE低8.9%~15.8%。
对NWP数据进行后处理可以提高模型精度,MEDINA等[27]比较了3种基于统计的后处理方法(非其次高斯回归、仿射核修整和贝叶斯模型平均)对ET0预报的提升效果,发现3种方法都能有效提高ET0预报精度。统计方法的不足之处在于通常只能单因素偏差校正,如使用辐射预报值跟辐射实测值建立关系。本研究发现,预报因子和对应的观测因子之间存在不匹配的问题,如与Tmin、RH最匹配的预报因子是Tmax,同样RH最相关的预报因子也是Tmax。也就是说名义上预报的某气象因子由于预测误差原因与实测的另一个气象因子的关系更加紧密。这首先由于气象因子之间本身就存在着互相影响的关系,如辐射是造成气温日变化的主要原因,同样气温会影响空气中容纳的水汽含量,进而影响到相对湿度;其次,可能是由于NWP产品基于物理模型,需要对气象要素之间复杂的非线性关系进行简化;最后,NWP的边界条件往往比较难以控制,这就造成了一定程度预报精度的下降[28],而部分有价值的信息被隐藏在了其他预报因子之中,使用LightGBM这类基于提升树的集合算法,可以将多维输入共同作为输入特征,发掘其中的非线性关系并剔除干扰特征。综上,推荐在对NWP数据进行偏差校正时,应考虑使用更多的相关因子建模,来改善NWP模型的不足。考虑到本研究中太阳辐射的预报精度还有待进一步提高,今后应使用数值天气预报中更多预报因子,如降水量、云量、反照率、土壤热通量等来提高太阳辐射的预报精度,进而进一步提升ET0预报能力。
4 结论
(1)预报因子与实测气象因子之间存在不匹配问题,其中太阳辐射的匹配度较高,最低气温、相对湿度的匹配度较低,需要借助最高气温等信息进行校正,使用多因子共同预报气象因子有助于气象因子校正。
(2)校正后统计指标显示,M3方法在太阳辐射、最高和最低气温、相对湿度和风速预报上均优于M1和M2方法。M1、M2和M3方法在9站点预报ET0平均RMSE分别介于0.66~0.93 mm/d、0.57~0.83 mm/d和0.53~0.79 mm/d,MAE分别介于0.44~0.61 mm/d、0.38~0.56 mm/d和0.35~0.53 mm/d,R2分别介于0.82~0.91、0.84~0.93和0.86~0.94。3种方法均在夏季误差最大,1~16 d平均RMSE分别为1.21、1.18、1.04 mm/d。
(3)各预报因子中太阳辐射对ET0预报误差影响最大,其后依次是风速、最高气温、相对湿度和最低气温。最高气温预报对其他因子预报精度的贡献最大、对相对湿度预报精度的贡献最小。

