移动并联式六自由度转运调姿方法研究

于荣荣 李永亮 董礼港 吕 宠 王国欣

(1.北京卫星制造厂有限公司， 北京 100094； 2.北京空间机电研究所， 北京 100094)

0 引言

在大型航天相机的辐射定标测试环节，需要对相机进行空间六自由度的姿态精确调整。目前，转运多采用吊车加专用转运工装方式，利用激光跟踪仪测量当前姿态和目标姿态，由人工对与调姿面连接的多个丝杠的高度进行反复手动调姿，直至调整至误差允许范围之内。这种调姿方法工作量大、工作效率低、操作繁琐，并且调姿精度低、产品风险高。随着航天相机功能的多样化，其结构越来越复杂，质量和尺寸越来越大，传统的调姿方法很难满足超大、超重载荷精确、快速和在有限空间内的柔性调姿要求。因此，需研发一种大型航天相机全自动六维姿态调整、转运一体化设备，这对提高大型相机转运及定标测试效率、提高产品安全性具有重要意义。

近年来，学者们对多自由度调姿方法进行了诸多研究：SHANG等[1]将并联机构(Parallel kinematics machine，PKM)引入飞机机翼柔性装配中。宋晨等[2]研发了一种具有串并联特征的六自由度调姿机构，用于小型喷嘴包调姿。尤晶晶等[3]进行了Stewart冗余并联机构正向运动学研究。敬兴久等[4]研发了一种基于气缸驱动的Stewart平台并联调姿机构，用于大型构件装配。顾营迎等[5]设计了六足平台，用于卫星平台微振动环境的地面测试。耿明超等[6]设计了6 UPRRUS 折叠式并联机构。文献[7-13]对3-RPS并联机构的结构、运动学、力学特性、标定方法等进行了研究，实现了柔顺控制，可用于踝关节康复训练等。文献[14-15]设计了航空发动机多自由度调姿装置。徐德勇等[16]设计了一种六自由度调姿平台。文献[17-19]对3T1R、3-RRPaR等多种并联机构进行了运动学分析。多数学者针对并联机构自身的结构特点和力学特性进行运动学分析、控制方法等方面的研究，而对复杂工况下任意姿态到目标姿态的量化及精确调姿方法研究却鲜见报道。本文针对使用需求，提出基于全向移动平台和3-RPS并联机构的移动并联式转运调姿方法，其中全向移动平台可实现相机长距离转运，并可完成相机在XOY平面内任意方向的运动和绕Z轴的旋转，并联机构可实现绕X、Y轴的转动和沿Z轴的平动。

1 系统概述

如图1所示，建立的坐标系1～6分别为：检测点坐标系O1X1Y1Z1、目标位置坐标系O2X2Y2Z2、相机端面坐标系O3X3Y3Z3、上平台形心坐标系O4X4Y4Z4、下平台形心坐标系O5X5Y5Z5、全向移动平台端面坐标系O6X6Y6Z6。

为了实现总装测试环节中，航天相机相对目标设备的精确瞄准，需要对相机进行六维位姿调整，本文将实际应用中基于精测的空间位姿调整问题，简化为目标坐标系和相机端面坐标系的位姿匹配问题，即通过调整全向移动平台和并联调姿机构的六维位姿，使坐标系3运动至与坐标系2重合，实现相机当前位姿向目标位姿的自动调整。系统工作流程为：①通过激光测距技术，由激光跟踪仪测得当前位姿下，相机端面相对于检测点的位姿、全向移动平台相对于检测点的位姿，实现相机端面、全向移动平台端面在全局坐标系下位姿参数的获取。②根据当前位姿、全向移动平台和并联机构的结构特点，建立位姿模型，利用矩阵变换理论解算各个坐标系之间的位姿变换矩阵，并获得相机当前位姿到目标位姿的位姿变换矩阵。③通过逆向运动学模型解算，将相机的位姿矩阵解耦为全向移动平台及并联调姿机构的位姿变换矩阵。④利用该矩阵反算得到全向移动平台和并联调姿机构各轴的运动参数，以该参数作为运动输入，解算各轴驱动量，通过多轴组合运动实现相机当前位置向目标位置的自动调整。

2 位姿矩阵解算

2.1 当前位姿解算

On1表示坐标系n相对于坐标系1(基准坐标系)的位姿矩阵，Gab表示坐标系a相对于坐标系b的位姿矩阵。激光跟踪仪分别测得坐标系3、6相对于基准坐标系的位姿矩阵O31和O61，再由坐标系1、2之间，3、4之间， 5、6之间的相对平移关系，可知其两两之间的位姿矩阵为

(1)

(2)

(3)

借助机器人运动学理论[20]，按照右乘法则，解算当前姿态下各坐标系在基准坐标系下的位姿矩阵分别为

(4)

则通过矩阵变换，获取的坐标系2～5相对于基准坐标系的位姿矩阵，即为各坐标系的当前位姿。

2.2 当前姿态相对于目标的姿态矩阵解算

如图2所示，姿态调整的目标姿态为：坐标系3借助调姿机构及全向移动平台的运动，与坐标系2重合。

假设此过程中，O3运动至O′3，O4运动至O′4，O5运动至O′5，O6运动至O′6。其中O3、O2重合，GO′3O2=I，GO′3O′4=GO3O4，GO′5O′6=GO5O6。则有

GO′3O2=I=GO′3O′4GO′4O′5GO′5O′6OO′6O2=GO3O4GO′4O′5GO5O6(GO′6O6OO6O2)

(5)

解算得

(6)

其中

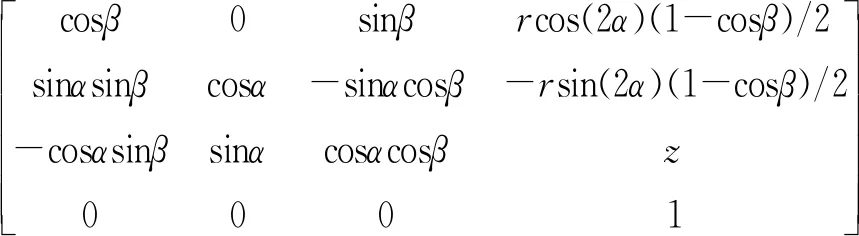
(7)

(8)

式中GO′4O′5——并联机构的当前姿态与目标姿态间的位姿变换矩阵

GO′6O6——全向移动平台的当前姿态与目标姿态间的位姿变换矩阵

并联机构运动到目标位置的过程为：先绕Y轴旋转β(俯仰)，再绕X轴旋转α(滚转)，然后升高到z，且俯仰和滚转运动中沿X轴方向和Y轴方向的伴随运动分别为rcos(2α)(1-cosβ)/2、-rsin(2α)(1-cosβ)/2[21]，其中r为动平台3个支点外接圆半径。全向移动平台运动到目标位置的过程为沿X和Y轴方向平移xveh和yveh、绕Z轴旋转γ。

将式(7)、(8)代入式(6)，根据实测的姿态矩阵和各坐标系之间的固有关系，可分别解算出全向移动平台及并联调姿机构的运动参数(xveh，yveh，γ)和(α，β，z)。

3 调姿运动实现

3.1 全向移动平台运动

为实现上述全向移动平台由当前姿态到目标姿态的各轴运动参数xveh、yveh、γ的自动调整，需建立全向移动平台的4个麦克纳姆轮全向轮组的运动学模型，解算各轮组运动和平台运动的关系，通过对轮组的协同控制，实现平台在平面内连续、高精度位置及角度调整,三维模型如图3a所示。

对建立的运动学模型构建如图3b所示的坐标系：参考坐标系O6-0X6-0Y6-0Z6-0以全向移动平台的位置中心为原点，坐标系O6-iX6-iY6-iZ6-i(i=1，2，3，4)以各个麦克纳姆轮位置中心为原点，各坐标系与全向移动平台端面坐标系O6X6Y6Z6均为平行系。假设坐标原点O6-0与O6-i在X轴方向距离为L，Y轴方向距离为l，车轮转动时线速度为viw，辊子和地面接触时的线速度为vir，车轮半径Rveh，辊子轴线与轮毂轴线夹角为α0，全向移动平台平移速度v=(vx，vy)，绕Z轴旋转角速度为ωz。根据运动学模型和逆向运动学分解，各个车轮转动角速度ωi(i=1，2，3，4)分别为

(9)

根据全向移动平台的各轴运动量，设定运动时间后，已知平台整体平移速度和绕中心的转动角速度，由式(9)可解算平台各个车轮转速，进而基于多轴协同控制实现当前姿态到目标姿态的3自由度自动调整。

3.2 并联调姿机构运动

为了实现并联调姿机构由当前姿态到目标姿态(α，β，z)的自动调整，对机构分析如下：并联机构采用3-RPS机构，如图4所示，其上下平台都是正三角形，两平台以3个分支相联，每个分支由3个运动关节连接，上平台各个支点分别连接一个球关节，下平台的每个支点各自连接一个转动关节，球关节和转动关节通过移动关节相连[22]。其中移动关节采用三级液压缸，电机驱动液压缸伸缩，通过杆长变化实现上平台俯仰、滚转和升降[23-25]。并联调姿机构的下平台外接圆半径R为525 mm，上平台外接圆半径r为425 mm，液压缸收缩态长度为440 mm，伸出态长度达1 050 mm，Z向可升高616.7 mm，满足大展收比的需求。

初始姿态下，以并联机构上下平台的形心为坐标原点建立的坐标系分别为O4X4Y4Z4和O5X5Y5Z5，目标姿态下，坐标系分别记为O′4X′4Y′4Z′4和O′5X′5Y′5Z′5。并联机构的结构特点确定了下平台支点Bi(i=1,2,3)在坐标系O′5X′5Y′5Z′5下的坐标(bXi，bYi，bZi)，再根据上平台支点Ai在上平台形心坐标系O′4X′4Y′4Z′4中的坐标(axi，ayi，azi)，将并联调姿机构的目标姿态代入式(5)可得目标姿态上、下平台形心坐标系的位姿关系GO′4O′5，则下平台各支点Bi在下平台形心坐标系下的坐标(aXi，aYi，aZi)为

[aXiaYiaZi1]T=GO′4O′5[axiayiazi1]T

(10)

可得目标姿态下，各缸长度为

(11)

通过控制3杆的长度进行所需目标姿态的精确调整。

4 调姿算法试验

设备实物如图5所示。在已知姿态下对调姿算法中所需的姿态矩阵进行测试，将实测姿态数据及各矩阵间姿态关系作为输入条件，调姿控制系统自动解算各轴运动量，验证移动并联式六自由度调姿技术的可行性。

为了便于测量，将目标位置设置为检测点，则GO2O1=I。且根据设备本身结构特点，姿态关系为

试验数据如表1所示。其中，初始姿态下相机端面坐标系O3X3Y3Z3、全向移动平台端面坐标系O3X3Y3Z3均与监测点坐标系平行，其他当前姿态为以初始姿态为基础进行的姿态转变，各轴运动量解算结果中，xveh与初始姿态下O31(1,4)对应，yveh与初始姿态下O31(2,4)对应，γ与对应的当前姿态下全向移动平台旋转角对应，l1、l2、l3与目标姿态下坐标系4和坐标系5的相对姿态有关。为了便于验证，表中目标姿态下坐标系4和5平行，高度差d为500 mm，因此并联调姿机构3杆长度应相同，均为

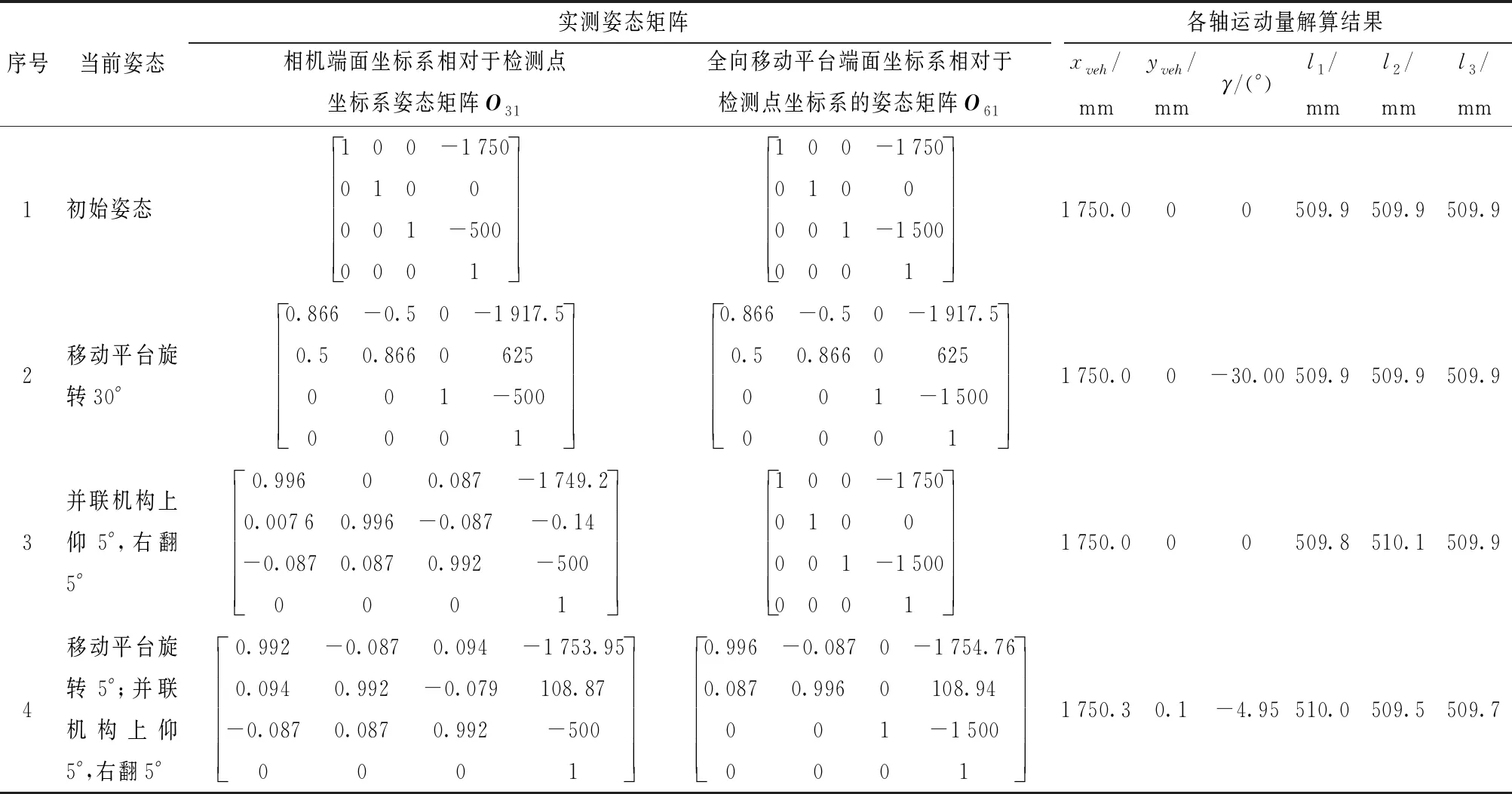
表1 调姿算法试验数据

经试验验证，基于移动并联式六自由度调姿技术将多轴耦合的空间六自由度完全解耦，实现全向移动平台和并联调姿机构分别调姿，姿态互补，调姿设备能够快速精准地实现大型相机任意姿态向目标姿态的自动化柔性姿态调整，全向移动平台移动精度优于0.3 mm，旋转精度优于0.05°，杆长精度优于0.5 mm，验证了调姿算法的可行性和准确性。

5 结束语

基于机器人运动学理论，对航天相机辐射定标测试阶段的自动调姿过程及快速调整算法进行了研究，提出一种基于激光测量和多姿态矩阵自动解算的移动并联式六自由度自动解耦算法。利用测得的实际姿态和各坐标系位姿关系，自动解算全向移动平台和并联调姿机构当前姿态到目标姿态的位姿变换矩阵，然后对各自由度解耦反算各轴的运动参数，通过控制全向移动平台麦克纳姆轮4个轮组的转动速度、方向和时间，控制并联调姿机构3杆长度，从而实现到目标姿态的自动调整。经试验验证，全向移动平台移动精度优于0.3 mm，旋转精度优于0.05°，杆长精度优于0.5 mm。