2UPR-RPS型并联机构精度设计

张 俊 池长城 蒋舒佳

(福州大学机械工程及自动化学院， 福州 350116)

0 引言

以并联机构为核心功能模块的混联加工单元具有大工作空间、高刚度、高灵活性等优点，正逐步应用于复杂零件的高效加工和精密装配[1-6]。运动精度是衡量该类装备使役性能的核心指标之一，特别是并联机构的末端位姿精度，一直是学术界和工业界的研究热点。一般而言，提高并联机构末端位姿精度的方法大致可分为运动学标定和精度设计两类[7-8]。运动学标定是在设备制造后，通过误差辨识和误差补偿来提高其运动精度；精度设计则是在设备制造前，通过合理分配零部件误差来提高其运动精度。

围绕并联机构的精度设计，一些学者已进行了相关研究。按其研究流程，精度设计一般包括误差分析和精度综合两个环节。误差分析的前提是误差建模，即建立机构几何误差源与其末端位姿误差的映射关系。根据所采用的不同数学工具，误差建模的方法大致有旋量法、一阶摄动法、D-H矩阵法和Grassman-Cayley代数法等[9-12]。ZHANG等[10]利用旋量法建立了4RSR-SS型并联机构的几何误差模型，并根据驱动螺旋和约束螺旋分离出可补偿误差源和不可补偿误差源。洪振宇等[11]采用摄动法解析了混联机械手Trivariant的不可补偿误差源，并借助灵敏度分析揭示了各不可补偿误差源对末端姿态误差的影响规律。LEE等[12]采用D-H矩阵法建立了三自由度平动并联机构的几何误差模型，得到影响平台位置精度的27个误差源，再通过标定仿真实验对误差模型的有效性进行了验证。为明晰误差源对末端位姿精度的影响，还需在误差建模的基础上进行误差灵敏度分析。常用的误差灵敏度分析方法有区间分析法、灵敏度系数法、蒙特卡洛法等[13-16]。构件的几何误差通常在一定范围内变化，而非一个固定值，因此区间分析法更适合于揭示误差源对末端位姿精度的影响规律。

精度综合是根据几何误差源对末端精度的影响，合理确定各误差源的取值，制定相应的零部件公差和装配策略，以满足期望的精度要求。目前，针对并联机构精度综合的研究较少。常见的精度综合方法有最小成本法、正交设计法、遗传算法等[17-23]。张为民等[20]基于雅可比旋量理论建立了公差数学模型，并通过遗传算法得到在保证装配要求下的公差优化分配。刘海涛等[21]基于小摄动原理建立了TriMule混联机器人的误差模型，并通过旋量法得到零部件公差与末端位姿的传递函数，再以最小成本为目标函数进行了机构的精度综合，实现了关键零部件的公差分配。WANG等[22]利用微分理论建立了3-R2H2S并联机器人的精度模型，基于误差独立性原理仿真出结构参数的误差分布。YAO等[23]基于最小制造成本建立了3RPS并联机构的精度综合模型，通过遗传算法求解非线性约束函数，得出关节间隙公差、支链杆长公差和转动关节公差等，仿真表明精度综合满足位姿精度要求。

本文以2UPR-RPS型并联机构为研究对象，探索过约束并联机构的精度设计方法。采用摄动法建立几何误差源与机构末端位姿误差的映射模型，并获得对末端位姿误差有影响的几何误差源。利用区间理论建立末端位姿精度关于几何误差源的灵敏度指标，通过灵敏度分析揭示几何误差源对末端位姿误差的影响程度。以灵敏度指标为权重建立机构的精度综合模型，获得各几何误差源的最优区间，并据此制定关键零部件的精度等级与配合公差。采用Sobol序列的拟蒙卡洛法对精度综合的结果进行评估，以验证所提精度设计方法的可行性。

1 误差建模

1.1 机构描述

以2UPR-RPS型并联机构为研究对象，开展机构精度设计研究。其机构运动简图和虚拟样机示意图如图1所示。

图1a中，B1和B2是2条UPR支链中虎克铰的几何中心点，A1、A2和B3是转动副的几何中心点，A3是RPS支链中球铰的几何中心点。静平台上△B1B2B3和动平台上△A1A2A3均为等腰三角形，其外接圆半径分别为b和a，且bi(i=1,2,3)和ai分别表示点O到点Bi的方向矢量和点O′到点Ai的方向矢量。另外,支链体上wi为BiAi方向矢量的单位矢量。基于图1a所示的拓扑构型，设计2UPR-RPS型并联机构模块的虚拟样机，其结果如图1b所示。它由静平台、动平台、2条UPR支链、1条RPS支链组成。在对称分布的2条UPR支链中，虎克铰与静平台连接，转动副与动平台连接，且两支链的虎克铰近架轴线共线，移动副轴线同时垂直于虎克铰远架轴线和转动副轴线。在RPS支链中，转动副与静平台连接，球铰链与动平台连接，移动副轴线通过球铰链几何中心点和转动副几何中心点且垂直于转动副轴线。

1.2 坐标系定义

为了方便建立该并联机构的误差模型，定义如图2所示的坐标系。

(1)静平台连体系{O}。如图1a所示，原点O在静平台的中心点，z轴垂直于静平台向下，y轴平行于水平面，x轴满足右手定则。

(2)动平台连体系{O′}。如图1a所示，原点O′在动平台中心点，z′轴垂直于动平台向外，y′轴平行于两转动副中心线，x′轴满足右手定则。

(3)UPR支链第i条关节坐标系{Oij}(i=1,2；j=1,2,3)。如图2a所示，{Oi1}为虎克铰坐标系，原点为虎克铰近架和远架公垂线与近架的交点，yi1轴沿近架轴线方向，zi1轴与公垂线重合，xi1轴满足右手定则；{Oi2}为支链i的连体系，原点为远架与支链的交点，xi2轴沿远架轴线方向，zi2轴沿支链i轴线方向，xi1轴满足右手定则；{Oi3}为支链i转动副坐标系，原点为转动副中点，xi3轴沿转动副方向，zi3轴垂直于动平台，yi3轴满足右手定则。

(4)RPS支链中关节坐标系为{O3j}(j=1,2,3,4)。如图2b所示，{O31}为支链转动副坐标系，原点为转动副中心点，y31轴沿转动副方向，z31轴垂直于静平台，x31轴满足右手定则；{O32}为支链体坐标系，原点为转动副中心点，y32轴沿转动副方向，z32轴沿支链体轴线方向，x32轴满足右手定则；{O33}为支链球铰坐标系，原点为球铰第一和第二轴线交点，x33轴沿球铰第二轴线方向，z32轴沿支链3轴线方向，y32轴满足右手定则；{O34}为动平台球铰坐标系，原点为球铰第三轴线中心点，x34轴与x33轴同向平行，y34与球铰第三转动轴线重合，z34满足右手定则。

2UPR-RPS并联机构误差源包括静平台、动平台位置误差，UPR支链、RPS支链等关节间的位置误差和姿态误差以及支链腿长误差，各几何误差源如表1所示。

表1 2UPR-RPS并联机构的几何误差源

1.3 误差映射模型

理想条件下，动平台坐标系相对于静平台坐标系的姿态变换矩阵R表示为

(1)

式中θ——绕y轴方向的转动角

ψ——绕x′轴方向的转动角

c表示余弦函数；s表示正弦函数。

动平台坐标系原点O′相对于静平台坐标系的位置矢量r可表示为

r=bi+qiwi-Rai(i=1,2,3)

(2)

其中

bi=b[cβisβi0]T
ai=a[cαisαi0]T
βi=αi=(-1)iπ/2(i=1,2)
β3=α3=2π

式中qi——支链BiAi的长度

当并联机构存在误差时，在一阶摄动下，点O′在UPR支链闭环矢量链和RPS支链闭环矢量链的位置矢量可分别表示为

r+Δr=bi+Δbi+(I+Δθi1×)Ri1[Δli2+
(I+Δθi2×)Ri2((qi+Δqi)e+Δli3)]-
(I+Δθ×)R(ai+Δai) (i=1,2)

(3)

r+Δr=b3+Δb3+(I+Δθ31×)R32(I+Δθ32×)·
[(q3+Δq3)e+Δl33+(I+Δθ33×)R33Δl34]-
(I+Δθ×)R(a3+Δa3)

(4)

其中

e=[0 0 1]T

(5)

式中I——三阶单位矩阵

Δθij×——Δθij的反对称矩阵

Δθ×——Δθ的反对称矩阵[11]

Rij(i=1,2；j=1,2,3)——第i条支链坐标系{Oij}相对于坐标系{Oi(j-1)}的旋转矩阵

R3j(j=2,3)——第3条支链坐标系{O3j}相对于坐标系{O3(j-1)}的旋转矩阵

将式(3)、(4)进行线性化，再与式(2)相减并忽略高阶项，可得到

Δr+Δθ×Rai=Δbi-RΔai+Ri1Δli2+
Δqiwi+Ri1Ri2Δli3+Ri1(Δθi2×Ri2qie)+
Δθi1×qiwi(i=1,2)

(6)

Δr+Δθ×Ra3=Δb3-RΔa3+Δq3w3+
R32R33Δl34+(R32Δθ32)×q3w3+
Δθ31×q3w3+R32Δl33

(7)

将式(6)、(7)两端分别点乘wi(i=1,2)和w3可得到

(8)

(9)

根据动平台的运动还受到UPR支链产生的沿着UPR转动副方向的约束力以及RPS支链上球铰几何中心沿着转动副方向的约束力。故并联机构不能产生沿着UPR支链约束力单位矢量vi(i=1,2)方向和RPS约束力单位矢量v3方向的移动[24]。

将式(6)、(7)分别点乘vi(i=1,2)和v3，则有

(10)

(11)

将式(8)～(11)化简并整理成矩阵形式可表示为

JE=Nε

(12)

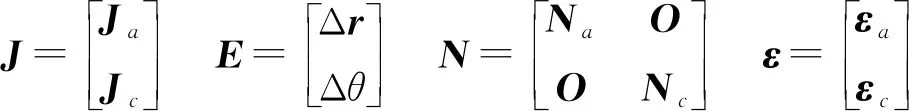
(13)

(14)

式中Ja——驱动雅可比矩阵

Jc——约束雅可比矩阵

O——零矩阵

εa——投影到驱动矢量上的误差源

Na——投影到驱动矢量上的误差系数矩阵

εc——投影到约束矢量上的误差源

Nc——投影到约束矢量上的误差系数矩阵

考虑到由误差模型得到的几何误差源εa和εc均对末端位姿精度产生影响，为保证机构具有一定的精度，对末端产生影响的几何误差源统一进行精度综合，以实现零部件误差的精度设计。

2 灵敏度分析

在制造和装配过程中，几何误差源通常在某个范围内变化而非一个固定值。因此，将几何误差源表示为区间向量形式，再借助区间分析理论对误差源进行灵敏度分析。

当并联机构处于非奇异位置时，式(12)可整理为

E=Gε

(15)

式中J-1——J的广义逆矩阵

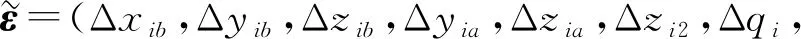
(16)

将式(16)表示为区间向量形式，则式(15)可转变为

(17)

(18)

其中

未来几十年，是江苏省全面建成小康社会、开启全面建设社会主义现代化新征程的关键时期，也是江苏省提升标准水平、高质量建设制造业强省的重要阶段。做好江苏省制造业标准化工作提升这项工作，意义重大，任务艰巨，时不我待。

(19)

其中

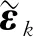
(20)

又由于机构的位姿误差随机构位形变化而变化，则可定义其在任务空间内的均值为灵敏度指标

(21)

式中V——任务空间体积

Kr,k——第k个误差源对位置误差Δr的灵敏度指标

Kθ,k——第k个误差源对姿态误差Δθ的灵敏度指标

设定机构尺寸参数和任务空间如下：动平台半径a=90 mm,静平台半径b=160 mm，最短腿长qmin=135 mm,最大腿长qmax=315 mm，z∈[110 mm,305 mm],θ∈[-30°,40°],ψ∈[-30°,30°]。

将式(16)的28个几何误差源从1～28进行排序，经计算得到几何误差源对末端位置误差Δr的灵敏度指标和姿态误差Δθ的灵敏度指标，其结果分别如图3、4所示。

从图3、4可知，末端位置对Δβi1、Δα31和Δα32较为敏感，其中，Δβi1为虎克铰近架绕y轴的转角误差，Δα31为RPS转动副的绕x轴的转角偏差、Δα32为RPS支链转动副与丝杠的垂直度误差。即这3项误差源对动平台位置精度产生较大的影响，因此在精度综合时应该将其进行缩紧处理。末端位置误差对Δx3a和Δx34不敏感，其中，Δx3a为动平台上半径a3沿x方向的尺寸误差，Δx34为球铰第一和第二转轴的装配误差。这些误差源对末端位置精度产生的影响较小，则在精度综合时应对其进行放松处理。

类似地，姿态误差对几何误差源Δβi1、Δα31和Δα32较为敏感，则在精度综合时应该对其进行缩紧处理；末端姿态误差对Δx34不敏感，说明该误差源对姿态影响很小，则在精度综合时应该将其进行放松处理，以降低制造成本。

3 精度综合

3.1 均匀设计法

由于在工作空间内进行所有位姿点的精度综合计算量较大，故本节采用均匀设计法来为精度综合提供合理的位姿点。采用极差法对并联机构的3个位姿参数进行水平划分和均匀设计表选择，其步骤如下：

(1) 设定几何误差源中位置误差为0.05 mm,姿态误差为0.025°,取表2中的ψ、θ和z任一位姿参数在其范围内变化，分别计算末端位置误差的极差值ΔrR和姿态误差的极差ΔθR，然后取两者极差值中的最大值为水平划分因子λ，其计算结果如表2所示。

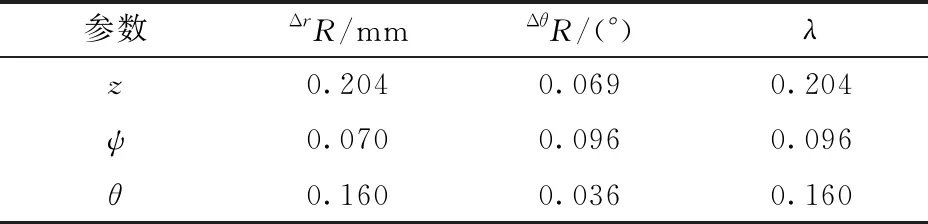
表2 位姿误差的极差值和水平划分因子

(2)以ψ的水平划分因子为基准，并考虑均匀设计的试验次数，取其水平数Lψ为13，则计算得到z的水平数Lz为26，θ的水平数Lθ为21(其中Lz=(λz/λψ)Lψ、Lθ=(λθ/λψ)Lψ，λψ为ψ的水平划分因子，λz为z的水平划分因子)。据此将θ在[-30°,40°]，ψ在[-30°,30°]以及z在[110 mm,305 mm]内分别等间隔且均匀地分成21、13、26份。

表3 位姿参数均匀设计

3.2 精度综合模型

由式(17)可得出末端位置误差末端和姿态误差模型为

(22)

由式(22)可得到

(23)

(24)

根据式(24)可得到Δr和Δθ的标准差为

(25)

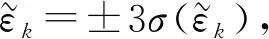
(26)

式中δr,k——第k个误差源独立作用下的局部位置误差

δθ,k——第k个误差源独立作用下的局部姿态误差

根据各个几何误差源对末端的位姿误差影响程度不同，本节引入位置误差灵敏度指标和姿态误差灵敏度指标为分配权重，则有

(27)

将式(27)代入式(26)，化简可得

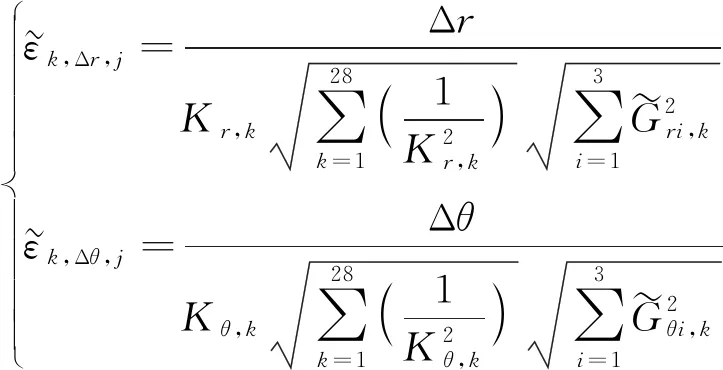
(28)

当给定末端精度条件，求解式(28)，并取其中最小值为第j个位姿下的第k个误差源的分配值，即

(29)

为得到最终精度综合结果，取所有位姿点下，误差源分配值的最小值为第k个误差源的精度综合最优解，即

(30)

将式(30)的误差源写成区间形式，则式(29)变为

(31)

设定末端精度条件为Δr=0.15 mm，Δθ=0.1°，并根据均匀设计表的位姿点和精度综合模型得到几何误差源的区间，其结果如表4所示。精度综合得到的误差源区间非零部件的制造公差，而是加工和装配共同作用达到的要求，故表5的误差源区间仅作为样机零部件公差设计和装配的参考。

表4 几何误差源区间

根据精度综合结果，对并联机构主要运动副进行精度等级划分和配合公差设计。其中主要的配合零部件有：各支链丝杠轴与支撑座轴承的配合、UPR虎克铰近架轴与轴承座轴承配合、UPR虎克铰远架轴与近架孔轴承配合、UPR转动副轴与关节座轴承配合、RPS转动副轴与轴承座轴承配合、RPS支链球轴架与对应轴承配合、RPS球副轴与关节座轴承配合。在保证降低成本和加工精度等级的条件下，制定了各零部件的精度等级和配合公差，如表5所示。其余非重要零部件的配合根据工程经验按IT 8～IT 11的精度等级制定。

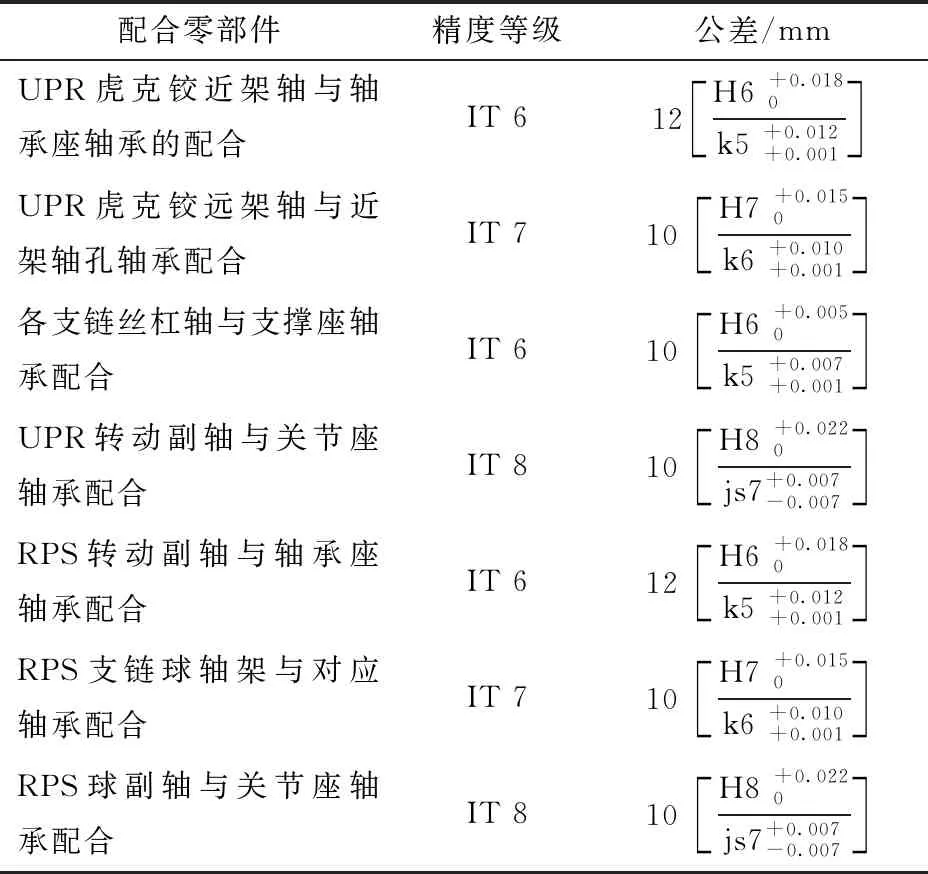
表5 关键零部件的精度等级及配合公差

4 精度预估

为验证精度综合方案的合理性，采用Sobol序列[25-26]的拟蒙特卡洛法进行精度预估，其中Sobol序列的产生原理如下：为产生序列x1,x2,…,xi(xi∈[0,1])，则需构造方向数i

(32)

式中mi——小于2i的正奇数

(33)

当i>d时，则有

(34)

式中 ⊕——十进制转换为二进制的异或运算

通过系数ai和式(32)可求得

i=2a1mi-1⊕22a2mi-2⊕…⊕2dadmi-d⊕mi-d

(35)

由式(35)可得到Sobol序列的第i个数为

xi=b1v1⊕b2v2⊕…⊕bivi

(36)

式中bi——i的二进制表示

为加快序列产生速度，将式(36)修正为

xi+1=xi⊕vi

(37)

根据式(32)～(37)可得到该并联机构的28个几何误差源的Sobol序列。

采用Sobol序列的拟蒙特卡洛法进行位姿误差分析，其步骤如下：

(1)在[0,1]内产生28个Sobol序列样本χj，其中χj=((x1)j,(x2)j,…，(x28)j)，j=1,2,…,M，M为位姿样本数。

(2)根据表4几何误差源的区间及其误差源的公差，将28个第j位姿点的Sobol序列样本转换为第j位姿点的几何误差源的样本ζj，其中ζj=((ε1)j,(ε2)j,…,(ε28)j)。

(3)在并联机构工作空间内随机且均匀产生位姿样本数M为2 000个，在每个位姿点处随机产生步骤(2)的几何误差源样本序列代入误差映射模型并经过计算得到末端的位姿误差。

依据上述步骤，得到末端位置误差和姿态误差分布，其结果分别如图5、6所示。

从图5、6可知，基于Sobol序列的拟蒙特卡洛法得到的位置误差普遍集中在0.15 mm内且Δr<0.15 mm的概率为99.95%；姿态误差普遍集中在0.1°内，且Δθ<0.1°的概率为99.95%，仿真结果表明精度设计达到了预期的精度要求。

5 结论

(1)采用一阶摄动法建立了2UPR-PRS型并联机构的误差映射模型，得到影响末端位姿精度的几何误差源。

(2)基于区间分析理论建立几何误差源的灵敏度指标，据此得出几何误差源对末端位姿误差的影响程度，其中末端位姿误差对误差源Δβi1、Δα31和Δα32较为敏感。

(3)以几何误差源的灵敏度指标为分配权重建立2UPR-RPS型并联机构的精度综合模型，并制定了关键零部件精度等级及配合公差。

(4)采用Sobol序列的拟蒙特卡洛法进行了机构精度预估，结果表明，位置误差小于0.15 mm的概率为99.95%，姿态误差小于0.1°的概率为99.95%，满足预设的末端位姿精度要求，从而验证了该精度设计方法的可行性和有效性。