基于空间轨迹的行星轮系移栽机构设计方法研究

王 磊 孙 良,2 徐亚丹 俞高红,2 张 委 郑 剑

(1.浙江理工大学机械与自动控制学院， 杭州 310018； 2.浙江省种植装备技术重点实验室， 杭州 310018；3.杭州职业技术学院， 杭州 310018； 4.杭州杭氧透平机械有限公司， 杭州 310004)

0 引言

非圆齿轮行星轮系移栽机构可由一套机构完成夹苗、拔苗、持苗和推苗等动作，其结构紧凑、工作平稳、成本低，并且可以设置多个移栽臂，从而实现高效移栽，已成为水旱田移栽机构研究的一个重要方向[1-4]。

目前，非圆齿轮行星轮系移栽机构设计方法主要包括给定机构参数(结构参数、运动参数)再进行优化的正向设计[5-7]和基于运动要求(轨迹、位姿)的逆向设计[8-10]。正向设计对机构参数的选择盲目性大，需要依靠专家经验，并且非圆齿轮节曲线方程的确定，使其变传动比特性不能得到充分体现。逆向设计可获得一般性的非圆齿轮副，且能实现机构参数与传动比、轨迹之间的关联设计。国内外专家学者相继提出了多种非圆齿轮行星轮系机构逆向设计方法[11-16]，这些方法主要集中在设计简单平面与球面轨迹的非圆齿轮行星轮系机构，关于由复杂空间轨迹逆向设计行星轮系机构的研究鲜有报道。

水稻钵苗宽窄行移栽是一种将水稻钵苗移栽和宽窄行种植优势相结合的种植方式，可有效提高水稻产量与质量[17-18]。而实现水稻钵苗宽窄行机械化移栽要求移栽机构能够形成一定的空间轨迹。TATSUYA等[19]首次将圆锥齿轮与非圆齿轮进行组合，通过参数优选得到适合日本水稻密植的空间轨迹。祝建彬等[20]设计了一种斜齿交错-非圆锥齿轮行星轮系分插机构，用来实现水稻毯苗宽窄行插秧空间轨迹。SUN等[21]基于空间位姿设计了一种平面非圆齿轮与交错斜齿轮组合传动的水稻钵苗宽窄行移栽机构，但该机构存在运动模型复杂、求解高次多项式方程繁琐、夹苗过程横向位移较大、影响夹苗成功率等问题。

为使行星轮系移栽机构能够实现复杂空间轨迹，更好地满足水稻钵苗宽窄行移栽的农艺要求，本文提出一种由一般空间连续封闭轨迹曲线逆向设计行星轮系机构的设计方法，包括建立基于给定空间轨迹的开链机构参数求解模型、总传动比求解、轮系组成分析与非圆齿轮设计等，并通过应用实例设计一种平面非圆齿轮与圆锥齿轮组合传动的水稻钵苗宽窄行移栽机构，以验证设计方法的正确性和可行性。

1 轮系机构简化与运动模型分析

由于单自由度两级传动(单行星架)行星轮系移栽机构运动轨迹为行星轮上某一点P所形成的，且一般情况下行星架的绝对运动为绕输入轴的平面转动，行星轮回转中心与机构末端点连线的绝对运动为往复摆动[22]。如果不考虑轮系中传动齿轮的啮合性能，可将此类行星轮系移栽机构简化为一般性的空间三杆二自由度(2R)的开链机构[23]，如图1所示。

图1中，杆件1表示轮系的行星架，杆件2表示栽植臂。以太阳轮回转中心O为原点，对空间开链2R机构建立坐标系xyz，z和z1分别表示机构的输入和输出轴，杆件1绕输入轴z转动，杆件2相对杆件1绕输出轴z1转动，在输入和输出轴的共同作用下机构末端点P形成轨迹C。利用D-H矩阵[20]可建立空间开链2R机构末端点P的运动轨迹数学表达式

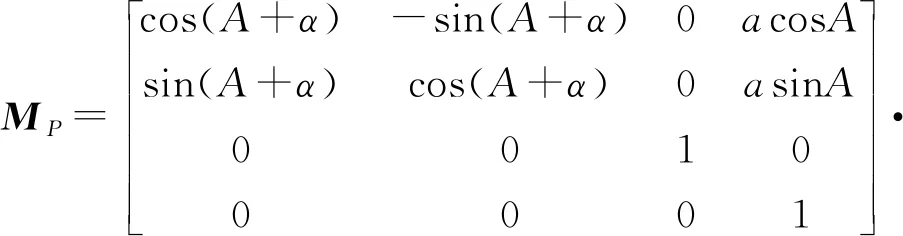
(1)

其中

A=θ-φ1B=γ+φ2

式中θ——杆件1的初始角

β——x1与xoy平面的夹角

α——x1在xoy平面的投影与杆件1的夹角

γ——杆件2的位置角

a、b——杆件1、2的长度

φ1——杆件1相对轴z的角位移

φ2——杆件2相对杆件1的角位移

角位移都以2π为周期。

对式(1)展开可得一个周期内空间开链2R机构末端点P的位移为

(2)

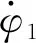
(3)

如果输出轴z1与输入轴z相交，即杆件1与输入输出轴共面时，则有

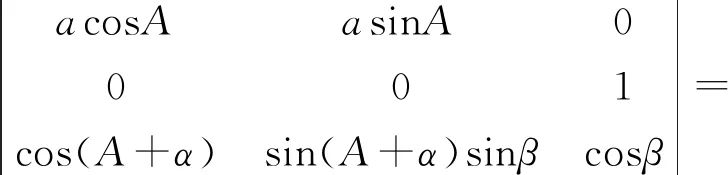
由于输出轴z1与输入轴z相交，故β≠0，因此α=0，此时点P的轨迹为球面封闭曲线，球心即为轴z1与轴z的交点。

2 基于空间轨迹的开链机构参数求解

2.1 空间轨迹表示方法

为了方便、直观地表示任意空间轨迹，本文采用3次非均匀B样条曲线拟合方法[24]对给定轨迹上的若干型值点数据进行拟合。

由n+1个多边形控制点定义的一条3次非均匀B样条曲线可以由分段有理B样条基函数表示[25]为

(4)

式中，Pi为控制顶点；u为节点参数；Ni,k(u)是由节点矢量U=(u0，u1，…，un+k+1)决定的k次规范B样条基函数。其递推公式为

(5)

其中，规定0/0=0。

由于运动轨迹为封闭曲线，若给定运动轨迹上一组有序型值点数据Qi(i=0，1，…，q)，为使3次非均匀B样条曲线通过给定的型值点，要求其首末端点分别与首末型值点一致，分段曲线的连结点需依次与曲线定义域内的节点一一对应，确定节点矢量U后可求出定义该3次非均匀B样条曲线的控制顶点，然后由控制顶点计算曲线各个点的坐标值，进而拟合出任意空间轨迹曲线[13]。

2.2 空间开链机构杆长求解

基于空间轨迹的行星轮系反求，首先需要求解简化模型空间开链2R机构的结构参数，即两杆的长度和输入输出轴之间的相对位置关系。

如图2所示，任意空间轨迹C位于参考系xyz中，假设轨迹C可由空间开链2R机构实现，点o1为坐标系z轴上的任意一点，假设以点o1为机构输入轴的回转中心，则转动副o1到轨迹C上各点的直线距离为L。若点n和m分别为轨迹C上距离点o1最近和最远的两个点，当空间开链2R机构末端运动到点n和m时，必然存在转动副位置k1(xk1，yk1，zk1)和k2(xk2，yk2，zk2)使得△o1nk2和△o1mk1垂直于xoy平面，令直线o1k1、o1k2长度为a，k1m、k2n长度为b，δ1、δ2分别为直线o1m、o1n与直线o1k1、o1k2的夹角。则可建立关系式

(6)

(7)

(8)

(9)

式中Lo1n、Lo1m——点o1与点n、m间的距离

联立式(6)～(9)可得空间开链2R机构的杆长

(10)

(11)

2.3 空间开链机构输出轴位置求解

如图3所示，若点h(xh，yh，zh)和j(xj，yj，zj)分别为轨迹C上具有z向坐标最大值和最小值的两个点，当空间开链2R机构末端点分别运动至点h和j时，图2中转动副k1和k2分别运动至k3(xk3，yk3，zk3)和k4(xk4，yk4，zk4)位置。如果输入轴z和输出轴z2为异面轴，则轴z2、直线k3h与直线k3z″位于同一平面内且垂直于xoy平面，同时轴z1、直线k4j与直线k4z′也位于同一平面内且垂直于xoy平面(其中直线k3z″、k4z′均平行于z轴)，即在空间开链2R机构的单个运动周期内，直线k4j与k4z′、k3h与k3z″在同一侧的夹角ζ1和ζ2达到机构在周期内的极值。令zz′=zj，zz″=zh，有

k4z′=|zk4-zz′|=bcosξ1

(12)

k3z″=|zk3-zz″|=bcosξ2

(13)

由于杆o1k3和o1k4在xy平面内运动，则点k3和k4的zk3、zk4值可由点o1的坐标值zo1确定，此时，可由式(12)、(13)分别求得ζ1、ζ2。

在空间开链2R机构运动过程中，轴z2(或z1)与直线k3z″(或k4z′)的相对位置不变，轴z1(或z2)与直线k4j(或k3h)的相对位置不变，即夹角η和λ均为常量，其值可由ζ1、ζ2确定，即

(14)

(15)

从而可以确定开链2R机构输入和输出轴之间的相对位置关系。

但由于给定轨迹并不一定满足异面轴传动条件，即在图3中点h和j具有z坐标最大和最小值时，转轴z2、直线k3h与直线k3z″并非满足共面的条件，而转轴z1、直线k4j与直线k4z′也可能不位于同一平面内。若如此，可以先假设在点h(或j)时轴z2、直线k3h与直线k3z″(或轴z1、直线k4j与直线k4z′)三线共面，由于轴z2(或轴z1)与直线k3h(或k4j)构成的面相对于轴z2(或轴z1)与直线k3z″(或k4z′)构成的面绕轴z2(或z1)转动，那么在轨迹C上必然存在一个点j′(或h′)，使得三线再次共面。具体计算时可先以拟合轨迹上z向坐标的最大值和最小值点初步确定输出轴位置角λ′、η′，然后在轨迹上寻找j′(或h′)点，最终获得满足交错轴运动要求的输出轴位置角λ、η。该方法虽然能求解输出轴的位置角，但获得的轨迹和期望轨迹之间会存在一定的差异，可在具体应用时进行判断与优化。

3 轮系机构转化与非圆齿轮设计

3.1 轮系机构齿轮组合分析

求解得到开链2R机构结构参数后，可通过在开链2R机构上依附不等速齿轮副将其自由度约束为1[14]。行星轮系移栽机构的设计以简单、高效、易实现为原则，因此本文的轮系组成分析主要针对单自由度两级齿轮传动的行星轮系机构。

(1)由上文分析可知，当给定轨迹C为平面封闭曲线，即输入与输出轴平行时，δ1=δ2=0，该轨迹对应的开链2R机构杆长为

(16)

由于输入与输出轴平行，只需用平面非圆齿轮副即可实现开链机构的不等速传动要求。

(2)当给定轨迹C为球面封闭曲线时，输入与输出轴相交，其交点即为该轨迹所在球面的球心，假设图2中点o1为此球心，则轨迹C上任意一点到点o1的距离均为球半径r，即Lo1m=Lo1n。由式(10)、(11)得a=0，b=r。此时图3中点k3、k4均与点o1重合，依然可利用2.3节所述方法确定输出轴相对于输入轴的位置。

对于这类输入与输出轴相交的行星轮系机构，可以采用非圆锥齿轮传动或平面非圆齿轮与圆锥齿轮组合传动等方式实现[14]。

(3)当给定轨迹为一般性空间封闭曲线，即开链2R机构输入与输出轴异面时，按照第2节所述方法可求得空间开链2R机构的杆长以及确定输出轴与输入轴的相对位置关系。其周转轮系可由平面非圆齿轮副与交错斜齿轮副、平面非圆齿轮副与偏置圆锥齿轮副、非圆锥齿轮副等多种可实现异面轴输出的齿轮组合形式来实现[21]。

3.2 传动比计算与非圆齿轮节曲线求解

在求得开链2R机构的杆长a、b及输出轴的位置角λ、η后，根据给定轨迹和开链机构在不同运动状态时的几何关系可求得杆件1的角位移φ1和杆件2相对杆件1的角位移φ2。则轮系机构的总传动比为

(17)

即行星轮系机构总传动比等于开链机构以杆件1角位移φ1为横坐标、以杆件2相对杆件1的角位移φ2为纵坐标的曲线斜率的倒数。得到机构传动比曲线后，可根据具体设计要求与齿轮组合形式进行传动比分配与齿轮节曲线求解，从而实现不等速行星轮系机构的设计[22]。

4 应用实例

4.1 水稻钵苗宽窄行移栽轨迹要求

水稻钵苗宽窄行移栽是在相同种植密度下，宽行与窄行间隔种植水稻钵苗的一种种植模式。目前，水稻宽窄行种植大多以宽行距400 mm，窄行距200 mm[17-18]为主，如图4所示，秧箱上相邻取苗位置之间的距离为300 mm，为了实现水稻宽窄行种植，需要一个空间轨迹来实现取苗处与推苗处之间的50 mm横向偏移量。同时考虑到水稻夹苗式取苗移栽的特点，提出了如图5所示的空间“8”字形移栽轨迹(型值点坐标数据如表1所示)，以实现水稻钵苗的宽窄行机械化种植。

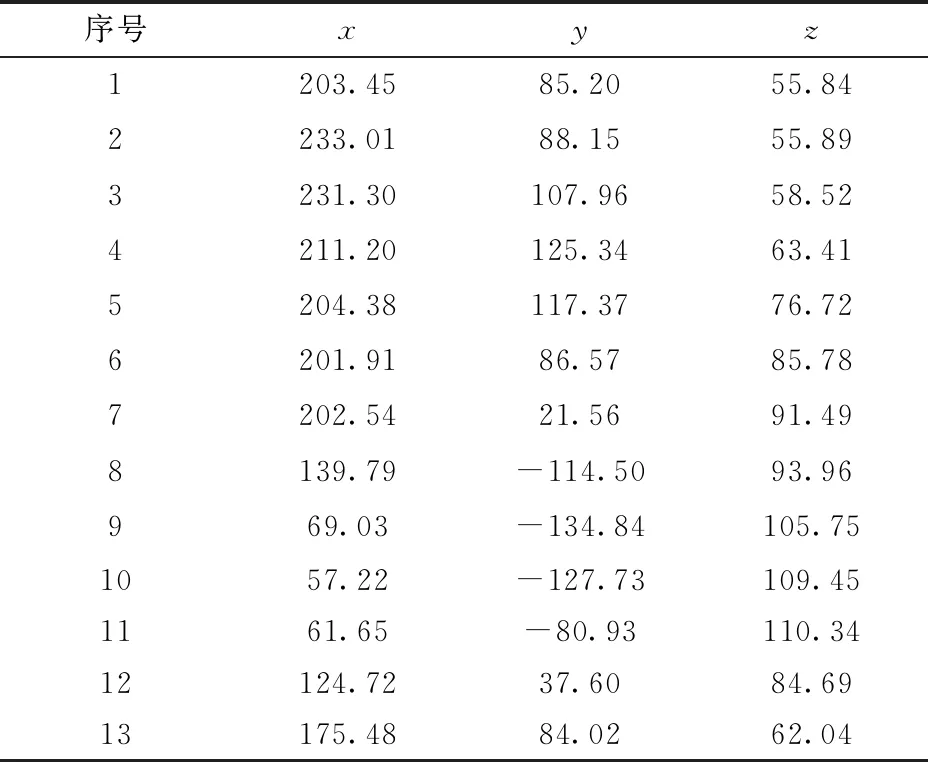
表1 型值点坐标数据

水稻钵苗宽窄行移栽机构需在单个工作周期内完成取秧、送秧、推秧及回程4个工作过程。如图5所示，点1～3为夹苗段轨迹，取苗爪从点1向点2运动(伸向钵盘)准备取秧，在点2～3段迅速夹紧秧苗，为了提高夹苗成功率，初步设计点1和点3之间的z向位移小于3 mm；经过点3～4段后将秧苗连带土钵从钵盘中拔出，此段要求两点之间的距离大于钵盘深度20 mm；点4～8轨迹段为持苗过程，至点9取苗爪松开秧苗，推秧部件作用于营养土钵并将秧苗推入田中，点2与点9之间要求有50 mm的z向位移；随后取苗爪再此向点1运动，为下次取秧做准备。

4.2 行星轮系移栽机构设计

基于4.1节提出的空间移栽轨迹，选择开链2R机构在点o1(0，0，0)处与机架构成转动副，此时轨迹上距离点o1最近和最远点分别为点12和点3，由式(8)～(11)可分别求解出开链2R机构中两杆的长度a=75.31 mm、b=214.27 mm。

点1为拟合轨迹上z向坐标最小的点(j点)，点11为轨迹上z向坐标最大的点(h点)，由式(12)～(15)可求得输出轴位置角λ=66.47°、η=8.78°，从而确定输出轴的位置。

因取苗环节的轨迹要求复杂，在反求传动比再现空间轨迹时选择点1为求解起始点。在已知开链2R机构具体参数的条件下，从型值点1开始由开链机构复演拟合轨迹，计算杆件的相对角位移，从而获得输出轴与输入轴间的传动比曲线(如图6所示)。

在得到机构总传动比曲线后，由3.1节可知通过依附不同类型不等速齿轮副缩减开链2R机构自由度，可获得多种能够实现空间轨迹的行星轮系移栽机构。本文采用结构简单、加工装配方便的平面非圆齿轮与圆锥齿轮组合传动，将平面非圆齿轮副置于第1级，圆锥齿轮副置于第2级，如图7所示。

由文献[21]可知平面齿轮与锥齿轮组合的行星轮系机构需采用折线布置。机构在图7所示初始位置时，l为机构输出轴在xoy平面上的投影直线，k为输出轴与xoy平面的交点。由于轮系第2级为圆锥齿轮副，且中间圆锥齿轮与中间平面非圆齿轮同轴布置，因此中间轴与行星轴相交(交点即为圆锥齿轮副的锥顶点)，又因为行星轮系第1级为平面非圆齿轮副，所以中间轴平行于输入轴(即z轴)，则中间轴在xoy平面上的投影为点p，且必定位于直线l上。点p位置的变化意味着平面非圆齿轮副中心距和圆锥齿轮副锥距的变化，应当根据轮系结构特点、齿轮节曲线的优劣对其进行优化。并且，移栽机构工作效果除轨迹影响外还对取苗推苗处的姿态有一定的要求，比如取苗角和推苗角要在一定范围内，其差值要近似于秧箱安装角等。

因此，为获得较优的移栽效果，在确定了理想移栽轨迹和开链2R机构结构参数的前提下，基于Matlab GUI开发了平面非圆齿轮-圆锥齿轮行星轮系钵苗宽窄行移栽机构优化设计软件，其运行界面如图8所示，主要包括模块：菜单栏①；设计参数区②；工具区③；图形显示区④；优化目标显示区⑤；优化结果显示区⑥。

通过调整相关设计参数，得到移栽机构中心轴回转中心点坐标为(-10 mm，47.65 mm，0 mm)，并求得输出轴与中间轴交点为(-10 mm，47.65 mm，-302.99 mm)，平面非圆齿轮副中心距为48.69 mm，由此求得平面非圆齿轮副节曲线，如图9所示。移栽机构的主要参数优化结果见表2，图10为参数示意图。

表2 移栽机构主要参数

根据优化后的移栽机构参数再现机构运动轨迹，如图11所示，可以看出机构再现轨迹与拟合轨迹存在一定的偏差，这主要是由于2.3节中提到的拟合轨迹不满足异面轴传动条件造成的，即该移栽轨迹上具有z向坐标最大值和最小值的点分别为点11和点1时，输出轴z2、直线k3h、直线k3z″，转轴z1、直线k4j、直线k4z′不同时满足位于同一平面的条件，在求解时先以拟合轨迹上点11和点1确定了输出轴位置角的初始值λ′、η′，然后计算得到点h′坐标值，并由点h′、点1及杆长计算得到输出轴的位置角λ和η。虽然以此求得的参数使机构复演的轨迹和期望轨迹之间存在一定的差异，但由图11可以看出，再现移栽轨迹在取秧过程和推秧过程都基本符合宽窄行钵苗移栽要求，并不影响水稻钵苗宽窄行移栽质量。

4.3 移栽机构仿真与试验

为了进一步验证理论方法的正确性和水稻钵苗宽窄行移栽机构设计的合理性，根据求解的机构结构参数和非圆齿轮节曲线，对水稻钵苗宽窄行移栽机构进行结构设计与三维建模，并在Adams软件中完成虚拟样机的仿真试验，得到移栽臂尖点的仿真运动轨迹，如图12所示。

利用3D打印技术加工移栽机构物理样机，并进行了空转试验，通过高速摄像机(Phantom系列)拍摄样机运动过程，再应用Blaster’s MAS图像分析软件捕获移栽臂末端点轨迹曲线，得到移栽机构实际运动轨迹如图13所示。

通过对比分析可知，所设计的夹苗式水稻钵苗宽窄行移栽机构的实际运动轨迹、仿真轨迹与理论复演轨迹基本一致，符合水稻钵苗宽窄行移栽的设计要求，验证了本文所提出设计方法的正确性和应用该方法设计夹苗式水稻钵苗宽窄行移栽机构的合理性。

5 结论

(1)提出了一种基于一般空间封闭轨迹曲线的行星轮系移栽机构逆向设计方法，建立了空间开链2R机构的运动学模型，根据杆件的空间几何关系求解得到了开链2R机构的结构参数，并由开链机构输入与输出轴间的相对角位移关系得到了轮系机构的总传动比，根据齿轮副组合类型进行传动比分配与非圆齿轮节曲线求解，从而实现单自由度两级传动行星轮系机构的设计。

(2)根据水稻钵苗宽窄行移栽农艺要求，结合B样条拟合方式获得理想移栽轨迹，利用本文提出的方法设计了一种平面非圆齿轮-圆锥齿轮组合传动的空间行星轮系水稻钵苗宽窄行移栽机构，并进行了虚拟仿真与样机试验，结果表明：实际运动轨迹、仿真轨迹与拟合的理想轨迹基本一致，可以满足水稻钵苗宽窄行移栽要求，验证了理论方法的正确性和可行性。