基于Kinect相机的油麦菜自动化三维点云重建

郑立华 王露寒 王敏娟 冀荣华

(中国农业大学现代精细农业系统集成研究教育部重点实验室， 北京 100083)

0 引言

利用计算机视觉技术对植物进行快速三维重建，获取植株的形态结构，并进行表型参数无损测量，可以客观反映植物生长状况[1-2]和关键性状[3-5]，为揭示植物生命科学规律、提高分子育种研究水平、发展精确农业管理模式提供科学依据[6-10]。

由于植物生长的复杂性和随机性，其三维模型的构建更为困难[11]。目前，基于温室或室外自然光照条件下的农作物三维点云重构技术日趋成熟，在农业领域的应用也愈加广泛和深入[12-17]。张慧春等[18]通过光学相机采集拟南芥植株的二维图像序列，利用运动中恢复结构 (Structure from motion, SfM) 算法生成了三维点云；梁秀英等[19]采集不同视角下的玉米植株图像，并利用基于SfM算法的Visual SfM软件获取玉米植株三维点云。以上研究侧重于植物表型参数提取，利用匹配算法从时间系列的二维图像中推算三维信息，并未针对植物三维点云进行自动化配准方法研究。郭彩玲等[20]利用地面三维激光扫描仪获取苹果树冠层三维点云，结合标靶球辅助进行配准，该方法保证了一定的配准精度，但存在数据采集设备成本过高的问题。

以Microsoft Kinect 2.0为代表的消费级深度相机具有性价比高、性能稳定等优点，利用该设备更容易获得高质量的三维图像。三维成像也已成为低成本农业应用中传感器设计、三维重建和表型分析[21]最具潜力的数据获取解决方案。但三维重建过程繁琐、复杂、费时费力，且三维点云配准精度得不到保证。KHOSHELHAM等[22]使用极线搜索方法将关键点从二维空间转换到三维空间，并根据深度测量的理论随机误差给定三维点的权重，从而提高了三维数据的准确性。郑立华等[23]通过引入初配准处理技术，获得了较好的点云初始相对位置，使果树精配准精度得到大幅提高。YE等[24]提出了一种利用颜色数据对深度数据进行配准的新方法，改进了迭代最近点(Iterative closest points, ICP)算法，并实现了更为准确的精配准精度。以上对三维点云重构技术的改进研究虽然未从根本上解决费时费力问题，但大大提高了点云配准精度。

单个Kinect一次只能从单视角对物体进行拍摄，无法获得物体完整的结构信息。贾鹤鸣等[25]提出一种将农作物放置于转盘上进行分角度拍摄的方法，将不同视角的点云按照原角度反转补充到目标点云空间中。但该研究配准结果受人为因素影响较大，且人力成本较高。

为探索基于多片点云的作物自动化三维重建方法，本文以油麦菜为研究对象，提出一套配准效果评价体系和一种三维点云自动重建算法，以实现油麦菜点云的全局三维重构，为器官分割和表型参数测定提供参考。

1 材料与方法

1.1 点云采集平台

如图1所示，数据采集设备包括：计算机，Microsoft Kinect 2.0相机，直径为40 cm的转盘。在转盘表面铺设一层标记有旋转刻度的漫反射白纸，白纸上标注了刻度，刻度间隔为22.5°。将油麦菜放置于转盘中心，为了获得视角清晰且质量较高的点云，将Kinect相机安装在三脚架上，使其正对转盘中心，调节镜头平面与转盘表面中心呈45°，距转盘表面的垂直高度为0.75 m。Kinect采集深度图像时易受环境影响产生噪声，在视野范围内应减少反光物体。油麦菜品种选择市面上常见的四季油麦菜(LactucasativaL. var.youmaicai)。

数据采集基于Ubuntu 18.04系统，配置Kinect相机驱动程序libfreenect2、PCL点云库、Open3D库[26]、ROS Melodic环境、Kinect的ROS接口工具和库IAI Kinect2。IAI Kinect2提供了深度图像和RGB图像融合生成点云工具，能够方便地保存实时深度图像、RGB图像和点云图像，并且包含Kinect标定工具以减少点云颜色映射错误。

1.2 相机标定

由于Kinect相机由位置不重合的彩色相机和深度(红外)相机组成，造成RGB图像和深度图像存在一定视差，从而导致融合后的原始点云存在颜色映射问题。为了获取高质量的原始点云数据，需要标定Kinect相机设备。针对一个5 mm×7 mm×30 mm国际象棋标定板，分别将Kinect相机置于距标定板0.6 m和1.5 m两个水平距离处，以世界坐标系X、Y、Z轴为旋转轴适度转动相机，从多个视角共采集200幅完整轮廓的棋盘格RGB图像、深度图像、RGB相机和深度相机同步图像，使用IAI Kinect2提供的标定工具对彩色相机和深度相机标定，计算转换矩阵，以校正点云，同时抑制镜头畸变。

1.3 数据获取及预处理

由于植物叶片位置及表面对光线的反射程度不同，以致单帧图像往往不能获取完整的数据，因此需要对同一视角下的多帧点云进行融合以获得较为稳定的点云。本研究连续采集50帧同一视角下的点云，点云类型为PointXYZRGBA。对50幅点云的相同点的X、Y、Z坐标值和RGB值求平均，形成新的点云图像，预处理后的点云有效减小了原始数据的噪声对配准结果的影响。

将标记有刻度的转盘(相邻刻度夹角为22.5°)逆时针转动，使RGB相机正对转盘中心及刻度线端点，每隔22.5°采集50幅点云图像，按以上方法进行数据融合，获得当前视角下的1幅三维点云图像，当转盘转过360°时得到16幅稳定的不同视角下的点云图像。

然后，采用直通滤波法将植株点云从包含背景的原始点云中分离出来。通过查看植株的最小包围盒，设置X、Y、Z轴方向的滤波尺寸为X(-0.2,0.2)、Y(-0.3,0.3)、Z(0.7,1.0)，从而提取研究对象点云。

本文随机选择了12株油麦菜(定植10～29 d)进行试验。为了进一步验证本文算法的效果，使用同样的方法采集了4株其他植物的三维点云数据，另外采用2组公共数据集的三维点云数据(http:∥graphics.stanford.edu/data/3Dscanrep/)进行验证。

1.4 点云配准算法

1.4.1点云初配准

初配准流程如图2所示。首先使用下采样方法分别计算并得到两片点云中的下采样点，随后计算这些点的快速点特征直方图 (Fast point feature histograms, FPFH)特征向量，基于Kd-Tree特征匹配算法匹配FPFH特征值从而获取两片点云之间的初步空间映射关系，继而利用随机采样一致性(Random sample consensus, RANSAC) 算法提取映射关系，获得源点云到目标点云的空间转换矩阵，完成初始配准。

1.4.2基于ICP的点云精配准算法

对于经过初配准后的源点云source以及目标点云target，使用Dmax表示两片点云中对应点最大距离，m表示迭代次数，则基于ICP的点云精配准步骤如下：

(1)若迭代次数小于m，则对每个在source中的点p，在target中找到距离其最近的点，距离小于Dmax的点集为本次迭代的对应点集。

(2)利用奇异值分解法(SVD)计算旋转矩阵Rm和平移矩阵Tm。

(3)计算source旋转平移后与target中对应点之间的均方误差dm。

(4)更新源点云sourcem=Rmsourcem-1+Tm。

(5)当旋转矩阵变化差值‖Rm-Rm-1‖2与平移矩阵变化差值‖Tm-Tm-1‖2均小于10-8或者|dm-dm-1|<10-8时结束迭代，否则返回步骤(1)。

ICP算法的输出结果为精确配准矩阵以及配准误差。

1.5 配准效果评价指标

为了实现两片油麦菜点云的自动化配准，本文在配准参数变化规律研究的基础上提出了配准效果评价指标体系，包括重叠率、离散度及距离误差。

1.5.1重叠率

配准能够达到的最好效果是两片点云相同的部分重合，不同的部分相互补充。可见，两片点云重叠部分的内点数对配准具有直接影响。实验发现，当两片点云重叠率不小于30%时，即能保障对样点云进行匹配关系提取后具有足够的对应内点个数，而内点数越多，即公共部分点云面契合程度越好，表示源点云进行空间变换后与目标点云相同部分的重叠程度越大，一定意义上可说明点云配准效果越好。本文将内点占全部下采样点的比值定义为重叠率，计算公式为

(1)

式中Pkey——源点云和目标点云中计算出来的所有下采样点数

Pin——RANSAC匹配关系提取后计算出的两片点云对应的内点总数

Roverlap——重叠率，%

为了保证足够的内点数，同时又能保证配准算法的效率，本文将下采样点数最小值定义为150，该设定值可以在不降低重叠率的前提下，保障较好的配准效率。

1.5.2离散度

单纯计算重叠率还不足以保障配准精度，当下采样点分布过于集中时，会造成局部下采样点重叠率高而整体配准效果不佳的情况，此时会出现两片点云部分重合但部分分层的现象。实验发现，提纯后内点之间的离散度越大，越能表现出点云的整体结构，点云配准效果越好。本文中，Kinect传感器以竖直方向为轴逆时针旋转拍摄油麦菜以获取点云数据，因此将下采样点的y坐标极差和z坐标极差之和定义为离散度，计算公式为

s=|ymax-ymin|+|zmax-zmin|

(2)

式中s——离散度，mm

ymax——y坐标轴方向最大值，mm

ymin——y坐标轴方向最小值，mm

zmax——z坐标轴方向最大值，mm

zmin——z坐标轴方向最小值，mm

1.5.3距离误差

为保证精度，在RANSAC提纯下采样点匹配关系时需要计算两片点云配准后对应点的距离误差，即均方根误差。距离误差越小，表示配准效果越好。

式中D——配准距离误差，mm

(xi,yi,zi)——配准后点云中对应点i的空间坐标，mm

(x′i,y′i,z′i)——配准后另一片点云中对应点i的空间坐标，mm

di——两个对应点之间的距离，mm

n——采样点数量，个

2 结果与分析

2.1 配准参数变化规律解析

两片点云配准过程中需要人工设置和调节的参数包括：点云下采样算法中的体素尺寸，FPFH特征描述子计算算法中的搜索半径和最大近邻点值，RANSAC提纯算法中的误差阈值和ICP精配准算法中的最大对应点距离。参数的合理设置决定了配准效果。实验发现，在不同拍摄距离和角度下，需要使用不同的参数才能获得最优配准效果。为了解决手动调整参数费时费力、目测配准效果误差较大等问题，本文研究了配准参数变化对配准效果的影响。

2.1.1下采样算法参数

下采样即对输入的点云创建三维体素栅格，并将每个体素中出现的点近似为它们的质心或中心。分别估计下采样前和下采样后的油麦菜点云法线及FPFH特征值并进行初配准，同时基于ICP对完成初配准的两片点云进行精配准。图3a对比了下采样前后的油麦菜点云配准消耗时间；图3b则对比了下采样前后的配准误差，使用均方根误差(Root mean square error，RMSE)作为评价指标。

图3a中，Time1、Time2分别为下采样前后初配准时间；Time3、Time4分别为下采样前后总配准时间。图3b中，RMSE1、RMSE2分别为下采样前后初配准误差；RMSE3、RMSE4分别为下采样前后最终配准误差。

分析实验结果发现，下采样能大幅节约初配准时间(RANSAC算法配准耗时)，以致于其总配准时间(RANSAC与ICP算法总耗时)大大缩短。虽然经下采样的点云在初配准阶段配准误差(RANSAC配准误差)较大，但可通过后期ICP配准弥补精度，使得最终配准误差(经ICP精配准后的误差)在可接受范围内。可见，下采样处理可大幅缩短配准时间且可获得相似的配准误差。

合理的下采样体素尺寸(Voxel size)对提升配准效率至关重要。实验发现，体素尺寸越大，下采样后保留的点云点数越少，其值决定了采样后的点云是否具有稳定性和代表性。而且，体素尺寸的取值范围为0.01～0.1时，具有较优的配准重叠率和均方根误差。以0.001为步长，在0.01～0.1范围内体素尺寸与初配准重叠率、RMSE的关系如图4a所示；其与初配准时间及配对点对数之间的关系如图4b所示。

配准实验结果表明，RMSE随体素尺寸的增大而增加，并逐渐趋于平缓，配准重叠率随体素尺寸的增大而增加，配准消耗时间和对应点对数均与体素尺寸成反比关系，综合考虑配准精度和配准效率，认为当体素尺寸取0.05时，点集稳定性和区别性最高。

2.1.2其他配准参数取值

FPFH用来描述点的某个邻域内空间的几何特征，邻域选取是否合理，决定了FPFH描述子是否能够准确地对下采样点所在局部空间的几何特征进行描述和区分。本文结合KNN和Radius Search计算FPFH特征值，包含搜索半径和最大近邻数两个关键参数。实验发现，当初始搜索半径为5倍体素尺寸、最大近邻数为100时，可保证初配准和精配准具有较优效果。在下采样点数量和FPFH特征值有保障的前提下，初配准后续的工作主要是为了提高配准精度，实验证明，RANSAC算法中的提纯距离误差阈值设置为1.5倍体素尺寸时(本文中提纯最大迭代次数内置为1 000)，即可为精配准提供良好的初始相对位置。

ICP算法中对应点距离阈值的合理设置能够减少精配准过程中产生的错误对应点，提高配准精度和配准速度。实验发现，当最大对应点距离阈值设为0.4倍体素尺寸时，可实现较高精度和效率的精配准。

2.2 两片点云自动化配准算法

两片点云的自动化配准算法流程如图5所示。

图6为其中两片油麦菜点云自动化配准的结果，图6a为初配准后获得的两片点云的相对位置，即将原始源点云经最优初配准转换矩阵转换到原始目标点云空间后的结果，图6b为经ICP精配准后获得的最终配准结果。对比发现，初配准的两片点云在叶片尖部未很好重合，存在错位现象；而精配准后的点云在相同部位叶片重合度较高，可见精配准进一步优化了空间转换矩阵，提高了两片点云间的配准精度。

利用两片点云自动化配准算法对16片原始点云进行两两配准，结果见表1中点云组1～8。初配准后点云距离误差为2.02 cm，配准耗时0.441 355 s；而精配准后点云距离误差减小到0.74 cm，配准耗时0.547 537 s，此时ICP只需几次迭代即可达到预设精度，可见合理的初配准转换矩阵对后续精配准结果至关重要。

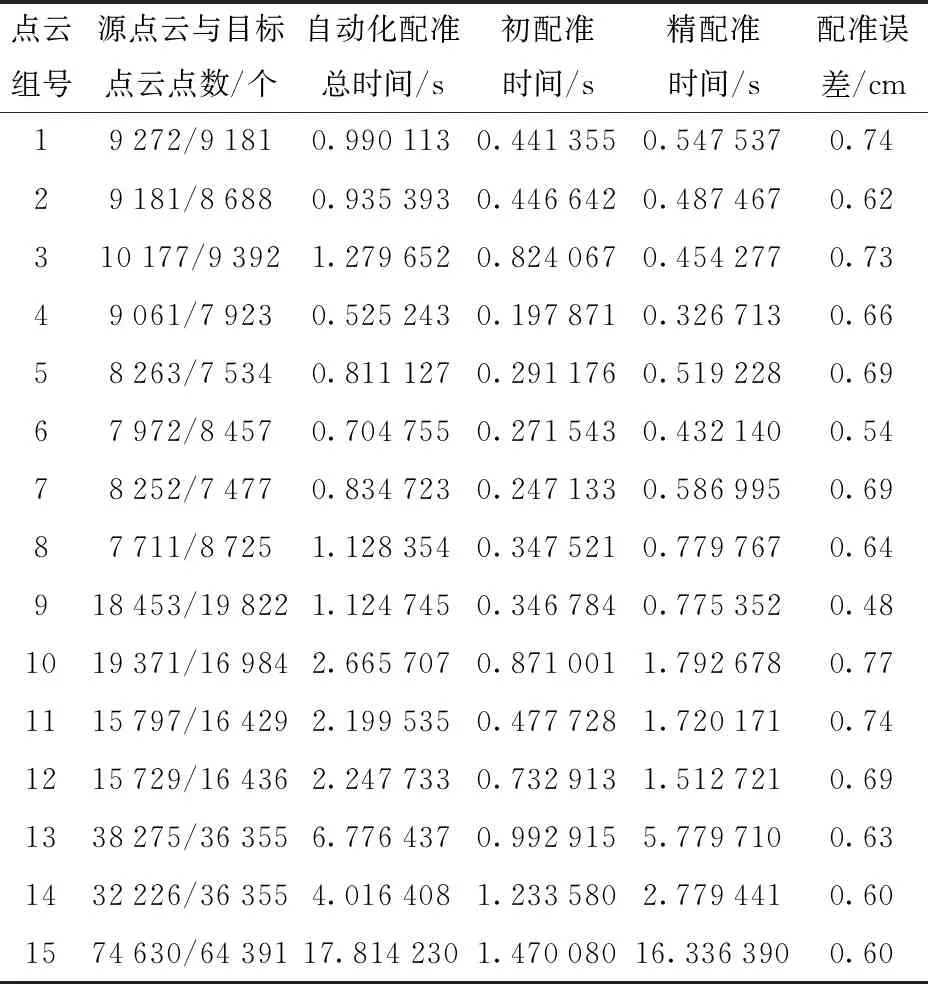
表1 平均配准时间及精度对比

需要说明，人工调参有可能找到更好的初配准位置，从而获得更高的配准精度，但需要投入大量的时间去反复尝试。本文算法对点云的适应性很强，在保证配准精度的前提下，有效避免了人工调节参数盲目性大、不确定性高、耗时较长且不易达到最优精度等缺点。

2.3 油麦菜点云全局三维重建

为了减小多次迭代误差累积，本文设计的配准流程见图7。

点云序列Pij(i=0,1,2,3,4;j=1,2,…,16/2i)表示经过第i次配准后的第j幅点云图像。对经过预处理后的16幅多视角点云进行第1阶段配准，分别对点云P01和点云P02、点云P03和点云P04、…、点云P015和点云P016进行两两配准，得到8幅点云；第2阶段对以上8幅点云按同样的方法两两配准，得到4幅点云；第3阶段对上述4幅点云进行两两配准得到2幅点云；最后对2幅点云配准完成全局重建，以上共经历15次配准。

1株油麦菜各个阶段的平均配准时间以及平均配准误差如表1所示。本文获取的原始点云图像中，每片点云包含7 000～11 000个点，对16片多视角点云全局配准后得到的全局点云图像平均包含139 021个点，即在油麦菜三维重建后，点云点数增加10倍以上。自动配准过程总消耗时间平均约为44.05 s，配准误差均值约为0.65 cm。结果表明，在保证配准误差精度的前提下，随着后续配准点云数目的累加，配准耗时大大增加，其中ICP精配准耗时占配准总时间比重大幅上升。但点云点数的增加并没有影响算法配准精度和最终配准结果，说明本文自动化三维重建算法对不同点云的适应性较强，可实现不同视角下油麦菜点云的自动化三维重建，在保证配准精度的前提下大大节省了人力和时间。

对采集的16片点云图像两两配准得到第1阶段配准结果(图8a)，基于第1阶段结果两两配准得到第2阶段配准结果(图8b)，重复以上步骤得到第3阶段配准结果(图8c)以及最终配准结果(图8d)。

在全局配准过程中，点云数目随着配准阶段增加呈2n级增长，配准效率大大降低，但配准误差维持在0.4～0.8 cm之间，在可接受的范围内。

为了进一步调查逐一累加点云配准和本文自动化配准方法的区别，在原始点云中随机挑选4组相邻点云进行配准，每组包含4片点云(由于传统累加点云配准方法往往会由于点云数量过多而导致配准精度过低，配准失败，本文选择4片点云进行不同方法的配准比较)，结果显示1～4组的传统递增式算法配准误差分别为4.44、3.52、4.19、4.61 cm，自动化配准算法配准误差分别为0.64、0.69、0.54、0.69 cm。使用本文算法进行油麦菜三维重建时，平均匹配误差由递增式配准时的4.19 cm降至0.64 cm，说明误差被均匀地分散到不同视角的点云配准中，从而削减了多次迭代引起的误差累积，保证了油麦菜三维重建的精度。

为验证该算法适用于多种形态油麦菜，对随机选取的12株样本进行了三维重建，结果如图9所示。结果表明，本文算法具有一定鲁棒性，但在叶片分层和叶片遮挡问题上还需要进一步优化。此外，为验证本文算法适合于其他植物，对Kinect采集的4株其他植物的点云进行了自动化三维重建，结果如图10所示，经统计配准误差分别为0.76、0.53、0.61、0.68 cm，平均误差为0.65 cm。最后，对The Stanford 3D Scanning Repository中的公共点云数据Armadillo[27]和Stanford Bunny[28]进行了重建，结果如图11所示，配准误差分别为0.61 cm和0.54 cm。结果表明，本文算法适用于多种物体的点云重建，并且当数据采集精度足够高时在配准中可有效避免叶片分层现象，并可应用于不同生长阶段的油麦菜重建，具有一定的鲁棒性。

3 结论

(1)由实验可知，RANSAC-ICP算法在相邻两片点云初配准、精配准过程中，其关键参数与配准效果之间存在确定的变化规律。

(2)提出的评价指标体系综合了算法效率和配准精度，并能够以此为算法控制条件实现两片点云的自动化配准，最终配准误差小于0.8 cm，配准消耗时间不超过0.6 s，有效避免了人工调节参数盲目性大、耗时较长且不易达到最优精度等问题。

(3)提出的油麦菜点云自动化三维重建方法减少了因多次迭代引起的误差累积，其自动全局配准过程总消耗时间平均约为44.05 s，配准误差均值为0.65 cm。本文算法为基于油麦菜三维点云的器官分割与表型无损测量奠定了基础，可为其他作物的三维重建及表型研究提供参考。