Influence of γ’ precipitate on deformation and fracture during creep in PM nickel-based superalloy

Zichao Peng,Jinwen Zou,Jie Yang,Gaofeng Tian,Xuqing Wang

Science and Technology on Advanced High Temperature Structural Materials Laboratory,Beijing Institute of Aeronautical Materials,AECC,Beijing,100095,China

Keywords:PM FGH96 superalloy Microtwinning γ′ precipitate Fracture mechanism Physically-based creep model

ABSTRACT FGH96 is a powder metallurgy nickel based superally used for turbine disk of aero-engines.In the present study FGH96 alloy with four different γ′ precipitate microstructures were produced via solution heat-treatment with different cooling rates,and the maximum cooling rate reached 400 °C/min which was a super cooling rate for Nickel-based superalloy.The creep tests were conducted for PM FGH96 alloy under the testing condition of 704°C and 690 MPa.The relationship between the creep properties and the distribution of γ’ precipitate was established.The creep mechanism was analyzed by using TEM and ACTEM,and the dislocation movement was studied at the atomic scale.The creep strain rate was calculated through a physically based crystal slip model established based on crystal plasticity.The calculated results were consistent with the test ones,illustrating the validity of the model.The fracture mechanism was also investigated,and the results showed that the creep cracks generated on the surface due to the oxidation.It was observed that the cracks propagated in different ways depending on the different average diameters of γ′ precipitate.With the decrease of the average γ’precipitate size,the critical shearing stress increased and the resistance of the dislocation slipping increased.The fracture mechanism for the primary stage transformed from intragranular to intergranular due to the change of dislocation slipping.

1.Introduction

The powder metallurgy(PM)Ni-based superalloy is extensively used in elevated temperature as the gas turbine disc due to its excellent tensile and creep properties.The excellent mechanical properties are derived from a coherent L12structure precipitate which strengthens the alloys by inhibiting dislocation movement [1–4].With the development of aviation industry,the velocity of the aircrafts increase significantly,leading to the requirement for the turbine disc materials to suffer from higher temperature and larger stress during the whole cruise.Therefore,the creep deformation will be more serious for the turbine disk superalloy.

The morphology and amount of γ′phase precipitates are important factors influencing the deformation resistance of Ni-based superalloy,and therefore the study on the relationship between precipitates and deformation property have been performed [4–7].Jackson [6]paid particular attention to the characterization of the γ′phase and found that an optimum size of 40 nm was the best for the creep property in Udimet720Li superalloy.The creep deformation mechanism has been studied and the physical model been constructed by Peng [4,7],and their results revealed that the critical shearing stress (CRSS) of γ′precipitate was demonstrated to be a significant factor for creep strain rate,and CRSS was mainly influenced by the size and fraction of γ′precipitate.The author’s group have studied the effect of γ′precipitate on the creep behavior of FGH96 superalloy,and found that the γ′precipitate was cut by partial dislocations and left micro-twins in γ′precipitate.The structure of microtwin in γ′precipitate with a diameter of 100 nm was studied,however,the details of stacking faults in smaller size γ′precipitate was not observed in FGH96 superalloy.Viswanathan [8,9]investigated the creep deformation mechanisms at intermediate temperatures in Rene 88DT superalloy,and the results showed that for the finer microstructure the anti-phase boundaries(APBs)only created in the tertiary γ′particles,while for the coarser microstructure the stacking faults (SFs) created in the secondary γ′precipitates.Therefore,the exactly strengthening mechanism for the γ′precipitate with the diameters between secondary γ′and tertiary γ′precipitates is still unclear.

Recently,it is realized that in order to improve the overall mechanic performance of most PM nickel-based alloys a rapid air cooling practice would be required,namely supercooling-treatment[10,11].Lin[12]has investigated the effects of solutionizing cooling processing on γ’’(Ni3Nb)phase and work hardening characteristics of a Ni–Fe–Cr-base superalloy.Feng [13]has studied the effect of cooling rate during quenching on creep property,and found that the creep resistance increased with the increase of the cooling rates.However,the largest cooling rate in Feng’s work was 232°C/min,which is not large enough to obtain the finer γ′phase as expected.To understand the strengthening mechanism of γ′precipitate in FGH96 superalloy,finer γ′phase(with the size smaller than 50 nm and under the cooling rate larger than 250°C min-1) should be obtained In this paper the solution treatment with different cooling rates and the maximum cooling rate of 400°C min-1has been carried out for PM FGH96 superalloy to obtain the γ′precipitates with various sizes The effect of the cooling rates on γ′precipitate of the alloy has been investigated,and the relationships between the cooling rate,average size of γ′precipitate and the creep properties established.The deformation mechanism of γ′precipitate has been studied at atomic scale by Double-spherical aberration correction transmission electron microscope(ACTEM),and the fracture mechanism of creep also studied.The results show that the size of γ′precipitate play a significant role on the deformation and fracture features during the creep.

2.Material and methods

The chemical composition(wt%)of FGH96 superalloy in was:12.9%Co,15.7%Cr,4%Mo,4%W,2.1%Al,3.7%Ti,0.7%Nb,0.05%C,0.03%B,0.05%Zr and balanced Ni.The FGH96 superalloy billet was prepared through the powder metallurgy (PM) method,including hot isostatic pressing,hot extrusion,isothermal forging.Then the forged materials were heat-treated with different cooling rates.The heat treatment parameters of the samples for creep tests were listed in Table 1.The cooling process was performed through the controlled cooling heat treatment furnace and the cooling medium was compressed air.The gauge section of the creep samples was a length of 25 mm and a diameter of 5 mm.The creep tests were carried out at 704°C and 690 MPa.All creep tests were terminated until the residual strain reached 0.1%,0.2%,and fractured.

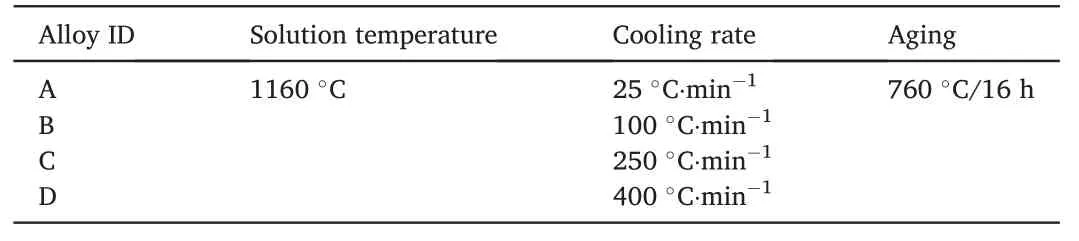
Table 1 Heat treatment parameters of the creep samples.

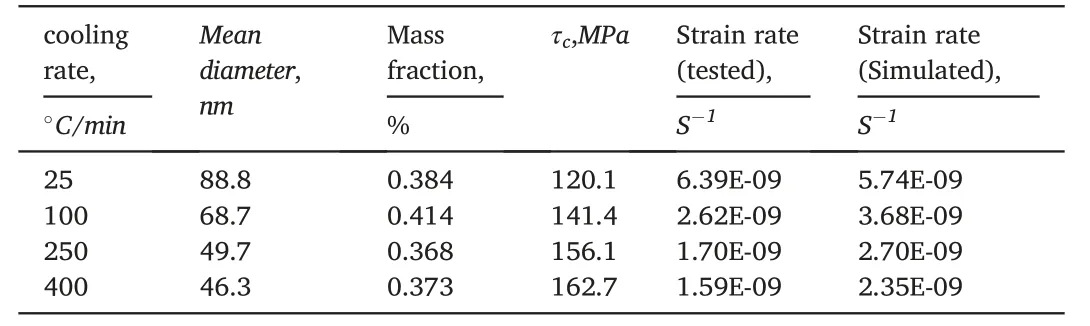
Table 2 CRSS and strain rates for FGH96 superalloy.

Fig.1.Grain boundary skeleton map of FGH96 superalloy with different cooling rates.

Fig.2.Microstructure characterization of γ′ precipitates.

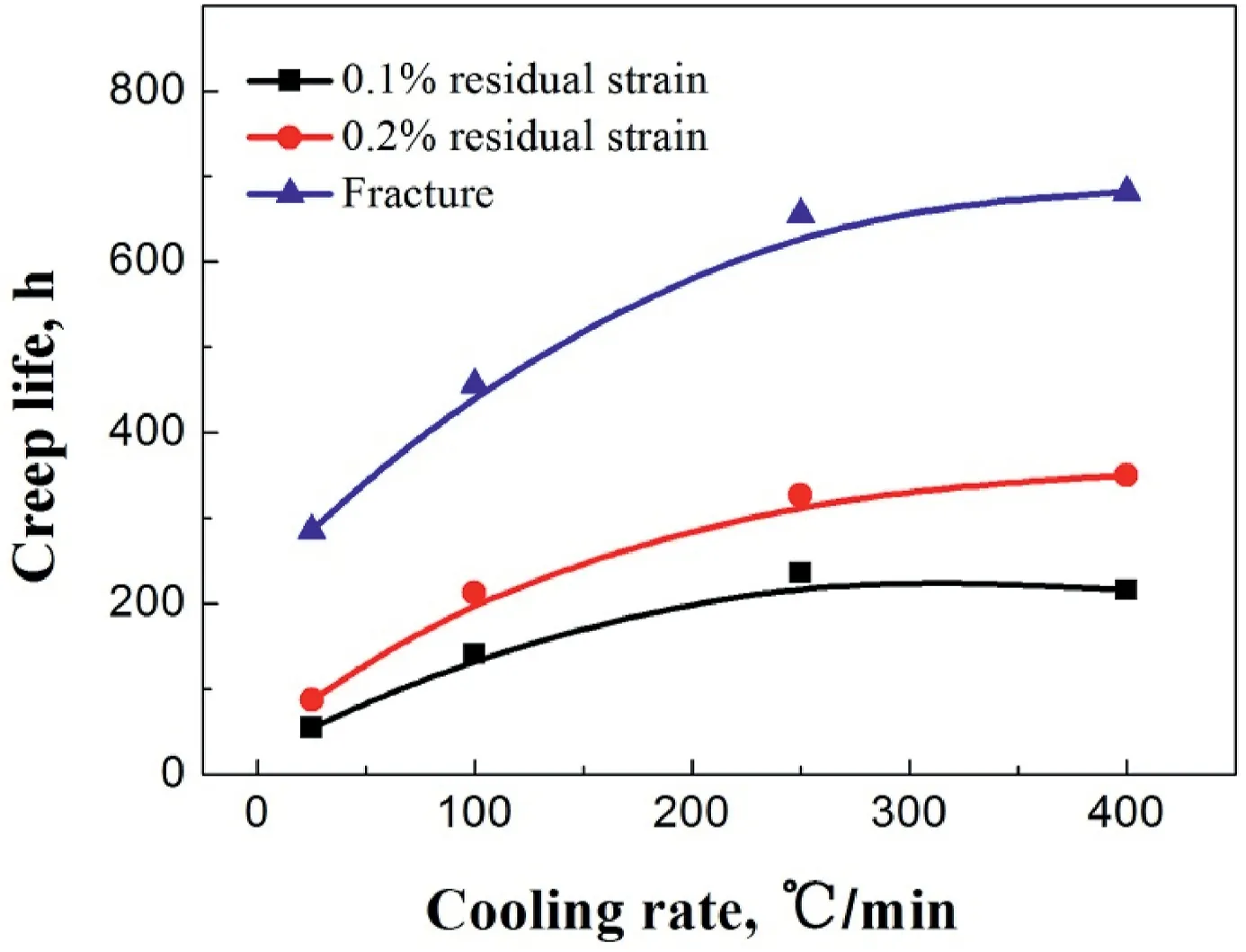
Fig.3.Relationship between creep life and cooling rate under the test condition of 704 °C/690 MPa.

The distribution of γ′precipitates was examined by scanning electron microscopy(SEM:Hitachi S-4800)and physics-chemical phase analysis.The γ′precipitate was firstly leached by electrolysis,then the size of γ’precipitate was analyzed by X-ray small-angle diffraction.The grain morphology features and local misorientation were characterized by electron backscattered diffraction(EBSD:Nordlys Nano-Quanta 650).

Transmission electron microscopy (TEM) observation foils were prepared from the standard gauge area of the creep specimens sectioned～45°to the stress axis.The twin-jet thinning technique was used to prepare TEM foils.The foils were analyzed by HR-TEM(FEITecnaiG2F20)and Double-spherical aberration correction transmission electron microscope(ACTEM) (FEI Titan Themis).

3.Results

3.1.Microstructure characterization

For nickel-based superalloy,grain boundary morphology was one of the important factors influencing creep property.Therefore,before the creep tests,the grain morphology of the specimens with different cooling rates was analyzed by EBSD,and the result is shown in Fig.1.In the grain boundary skeleton map,the black lines corresponded to large-angle boundaries with misorientation angle tolerance larger than 10°,the red lines represented annealing twins (‘special boundary’Σ3,where the Σ3 coincident site lattice is a 60°<111>grain boundary) due to the low stacking fault energy of the material.The Σ3 boundary has been proved to be favorable for creep resistence[7].The frequency of the small-angle boundaries with the misorientation angle tolerance smaller than 10°was so small that could be negligible in this work.Although the alloys were treated with different cooling rates,the grain morphology and grain size were similar.The frequencies of Σ3 boundary were between 56% and 58%,which would not bring a difference to the creep test results.

Fig.4.TEM analysis of FGH96 superalloy with different cooling rate.

Fig.5.Intersecting surface of FGH96 superalloy with different solution temperatures.

Fig.6.Fractographs of FGH96superalloy with cooling rate at 400 °C/min.

The morphology and distribution of γ′precipitates are shown in Fig.2.After supersolvus solution treatment,there was no primary γ′phase located at the grain boundary in all specimens.Similar to the results of other published studies[1,13],with the increase of cooling rate the average size of γ′precipitates decreased.However,another phenomenon was found that the width of size distribution was narrower when the cooling rate was larger than 250°C min-1.The secondary and tertiary γ′precipitates were found to exist in the specimens with a cooling rate below 250°C min-1.However,after the cooling rate reached at 250°C min-1,the secondary and tertiary γ′precipitates could not be distinguished easily through SEM graphs.It is believed that the larger cooling rate would lead to the outbreak of γ′nucleation and limit the growth of the γ’ precipitate.Besides,after solution treatment the lower supersaturation degree in the matrix would result in a very small amount of supplement precipitation during aging treatment.

3.2.Creep results

The creep tests were performed under the condition of 704°C/690 MPa,and were terminated when the strain of 0.1%,0.2% had been achieved or fractured.The temperature and stress of the creep were determined according to the service condition of the turbine disk,and this condition was always used for creep study in FGH96 superalloy[4,7,13].The relationship between the creep life and cooling rates were shown in Fig.3.As shown in Fig.3,the creep life increased with the increase of the cooling rate,no matter the residual strain arrived at 0.1%,0.2%,or fractured.However,when the cooling rate arrived at 250°C/min,the creep life increased slowly.

4.Discussion

4.1.Influence of γ’ precipitates on creep mechanism

After the creep tests,TEM analysis was performed to study the deformation mechanism of the creep.Fig.4 was the microstructure characterization of FGH96 superalloy with 0.2%residual strain.Similar to that of SEM analysis,the diameters of γ′precipitates(higher brightness area) were about 100 nm in alloy A and 40 nm in alloy D.Several slip bands were observed in both alloy A and D,and the γ′precipitates were both sheared by coupled-dislocations.Due to the shearing of dislocation,the stacking faults generated within γ′precipitates,and the details of stacking faults were analyzed at the atomic scale by ACTEM,as shown in Fig.4.ACTEM results showed that the stacking faults were both extending along <-2 1-1>direction and {1 1 -1} plane of the γ′precipitate,and the stacking faults had typical twinning characteristics.According to the results of Viswanathan and Karthikeyan[14–16]that all the twinning partials had the same Burgers vector of the 1/6<112>type,and these partials traveled on adjacent parallel {1 1 1} planes and then formed microtwin inside the γ’ precipitate.The thickness of the microtwin was defined here by the number of adjacent{1 1 1}planes that had been sheared by partial dislocations.

Fig.7.Fractographs of primary stages of FGH96 superalloy with various cooling rates.

Even if the γ′size refined to 40 nm the microtwinning was still the main deformation mechanism for the FGH96 superalloy.However,as discussed above,APBs were mainly created in tertiary γ′precipitates with a diameter of less than 20 nm.Therefore,there must be a critical size of γ′precipitates for the shearing mechanism transferred from microtwinning to APBs.Besides,the reason for the change in the shearing mechanism was also of great value to the γ’ precipitates strengthening of PM superalloys.

According to a physically-based creep model,the creep strain rate could be calculated as follows[4]:

In which ρgis the density of gliding dislocations,b is Burger’s vector magnitude,ν is the frequency of dislocations attempting to jump across the energy barriers,kbis the Boltzman constant,T is the absolute temperature,ΔF is the Helmholtz free energy,ΔV is the activation volume,σ is the applied stress,θ is the angle between the loading direction and slip direction,φ is the angle between the loading direction and slip plane normal,and τcis the critical shearing stress(CRSS).For the four types of FGH96superalloys,τcwas the single factor to influence ˙γ.There were two models to calculate τc,namely the weakly-coupled model and the strongly-coupled model[17].A critical precipitate radius rc(about 20 nm for FGH96)was the decisive factor of the CRSS model.

The mean diameter and mass fraction of the γ’ precipitate were calculated by the physics-chemical phase analysis,as shown in Table 2.The minimum mean diameter was 46.3 nm,which was larger than rc.Therefore,τcwas controlled by a strongly-coupled model and could be calculated as:

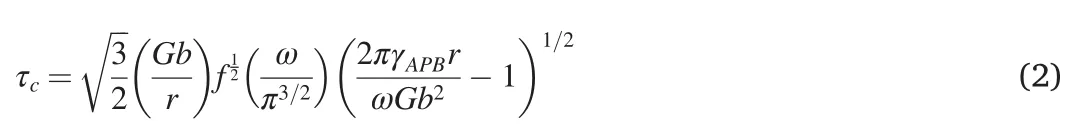
where G is the isotropic elastic shear modulus,f is the volume fraction of γ′phase,r is the average radius of the precipitate,ω is a constant which accounts for the elastic repulsion between the strongly paired dislocations,and γAPBis the APB energy,～0.279 J/m2at 700°C[18].

The critical resolved shear stresses for each different heat-treated FGH96 superalloy are obtained by bringing mean diameters and mass fractions into equation (2),then substituted τcinto equation (1) to calculate the strain rate.The values of critical shearing stress and strain rate were both calculated and shown in Table 2.There was an obvious rule that a smaller size of γ’phase would result in larger critical shearing stress and lower the strain rate.

The results of the calculation indicated that the simulated strain rates are equal to that of the tested strain rates.Therefore,the physical-based creep model is suitable to estimate the creep strain rate of FGH96 superalloy when the size of γ’phase is the main influencing factor.It may be a good method to evaluate the creep property of FGH96 superalloy without long time tests,and can be used to instruct the supercooling process.

4.2.Fracture mechanism of creep

The fracture morphology of FGH96 superalloy was further analyzed by OM,SEM,and EBSD to understand the fracture mechanism.Fig.5 is the intersecting surface of FGH96 superalloy with different cooling rates.It was observed from Fig.5a that there were a large number of creep cracks on the surface of the crept samples,and the crack propagation direction was perpendicular to the loading direction.These fracture characteristics indicated that the creep cracks originated on the surface and extending inward.

The origin of surface creep cracking could be explained through the longitudinal cut of the creep specimen by SEM (Fig.5b).The SEM observation showed that the grain boundary delineated by dark oxide products which leads to the formation of cracks along the grain boundaries.Oxide debris was visible on the surface and was also noted in the wake of the primary crack on the specimen surface [19,20].This indicated that the crack initiation is partly due to grain boundary oxidation in addition to the potential effect from the subsurface pore.The grain boundary oxide debris along the surface of the primary crack in the creep samples was noted at the early stage of the test.Besides,there was a γ′-depletion layer along the creep crack,as shown in Fig.5b,which was the further evidence supporting the crack initiation from the specimen surface,and growing along the grain boundary on the primary stage of crack propagation.

Fig.8.EBSD maps from a region around creep crack tips for the primary cracking stage.

Fig.6 is the fractography of the crept specimen with cooling rates at 400°C/min analyzed by SEM,in which the fracture feature changed with the growth of cracks.At the primary stage,the cracks grew along the grain boundary and intergranular fractures can be observed(see Fig.6b).With the acceleration of the crack propagation rate the fracture mode was transformed into a mix of intergranular and transgranular.There were a large number of cleavage planes and dimples in the fractography(Fig.6c).At the last stage (Fig.6d),the fracture feature was the typical dimple feature[20].

There was no difference in the fractures of secondary and last crack growth stages when the cooling rates were different,however,the fractography of the primary stage was changing with the cooling rates.The fractography of the primary crack growth stage was shown in Fig.7,which indicated that there were some different features in the specimens with different cooling rates.With the increase of cooling rates the intergranular fracture features were more obvious.The fractures of alloy A and alloy B were a mix of intergranular and transgranular,namely the intergranular and transgranular features were both located in the fractures.When the cooling rate was larger than 250°C/min,the fracture features were typical intergranular.The phenomenon that failure pattern changed from the mixed intergranular/transgranular mode to the intergranular mode was also found in other Ni-based superalloys[21].

The fracture characteristics were also evaluated by EBSD analysis at the tip of the creep crack.As described above,the creep cracks generated on the surface of the alloys,and firstly propagated along the grain boundary.The Band Contrast (BC) and Kernel Averaged Misorientation(KAM)maps of creep tip in this stage were shown in Fig.8.The BC maps clearly showed that there were a large number of slip bands generated in the alloys after the creep deformation,which affirmed that slipping was the main deformation mechanism of creep in FGH96 superalloy.Besides,due to the increase of CRSS resulted from various average diameters of γ′phase the number of the slip bands decreased.As discussed above,the finer size γ’phase offered larger resistance effects to the dislocations and inhibited slip deformation.Therefore,relatively few slips bands existed in alloy C and alloy D.

Several studies showed that KAM was correlated well with the magnitude of microstructure scale deformation,such as plastic strain and accumulated fatigue damage [20–24].In KAM maps,the brighter color represented the larger value of KAM also represented the larger plastic deformation.In Fig.8,it was obvious that the value of KAM decreased with an increase of cooling rate.When the cooling rates were 25°C/min and 100°C/min,the larger plastic (brighter color areas) strain located along the grain boundary and slip bands.However,the larger plastic strain concentrated on the grain boundary due to less quantity of slip bands when the cooling rates were 250°C/min and 400°C/min.

In general,the cracks grow along with the areas with weaker toughness.For alloy A,the grain boundaries and slip bands were the areas with weaker toughness because of larger plastic strain.Therefore,the cracks grew along the grain boundaries or slip bands.When it grew along with grain boundaries the fracture model was intergranular.When it grew along with slip bands the fracture model was intragranular.This was just the reason for the mixed fracture features of intergranular and transgranular.

However,for alloy D,at the primary stage of fracture the larger plastic strain only concentrated along the grain boundaries,which resulted in the intergranular fracture.With the crack growth the opening displacement of the cracks was enlarged,resulting in an accumulation of the stress around the crack tip.Because of the increase of the stress field around the crack tip the plastic strain distribution was not only along the grain boundary,instead there was larger plastic deformation occurred both at the grain interior and grain boundary area near the crack tip,as shown in Fig.9.Therefore,the crack propagation path was not along the grain boundary but grew along the area with the largest plastic deformation or other defects.At this time,the creep fractures mechanism transformed from intergranular to the mixed model.

Fig.9.EBSD maps from a region around creep crack tips for the secondary cracking stage in alloys D (a) BC map,(b) Euler angle map,(c) KAM map.

5.Conclusions

The relationship between the cooling rate,morphology of γ’ precipitate and creep property of PM FGH96 superalloyduring creep tests at 704°C and 690 MPa has been investigated.

(1) With the increase of the cooling rate the average size of γ′precipitates decreases,and the width of the size distribution become narrower.When the cooling rate is 400°C/min the size of γ′precipitates reaches to 40 nm,which can be used to guide the supercooling study for the turbine disc.

(2) Even the size of γ′precipitates is smaller than 50 nm,the deformation mechanism is still microtwining.However,there must be a critical size of γ′precipitates for the shearing mechanism transferred from microtwinning to APBs.

(3) The critical shearing stress increases with the decrease of γ′size,leading to better creep property of FGH96 superalloy.An effective creep model established based on crystal plasticity theory can predict the steady creep rate.

(4) With the decrease of average size of γ′precipitates,the critical shearing stress increases and improves the resistance of dislocation slipping,and the fracture mechanism for the primary stage transforms from intragranular to intergranular.For the alloy with γ′precipitate smaller than 50 nm,the creep fracture mechanism also transforms from intergranular to intragranular due to the enlargement of crack opening displacement and the increase of stress field around the crack tip.

Data availability

The raw/processed data required to reproduce these findings cannot be shared as this time as the data also forms part of an ongoing study.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgments

The project is funded by The National Science Key Lab Fund(No.6142903190303).The authors thank Ying Yang of Beijing center for physical and chemical analysis for her careful instruction on EBSD.