基于CNN-RF滚动轴承故障诊断研究

周 杨

（浙江海洋大学 海洋工程装备学院，舟山316022）

轴承作为工业设备当中的重要部件之一，其性能的好坏直接影响到设备是否能正常运行。根据有关数据统计，旋转机械的故障约有三分之一是由轴承故障引起的[1]。所以，研究轴承故障并确定故障类型成为了国内外的热门研究领域之一。

轴承故障诊断的研究核心是信号的特征提取和故障分类。文献[2]提出了经验模式分解（empirical mode decomposition，EMD），这是一种新型自适应信号的时频处理方法，特别适用于非线性非平稳信号的分析处理。但是，这些时频处理方法，需要人工手动提取且要有丰富的专业知识。最近几年，随着科技的不断进步，以机器学习为基础的数据驱动的故障诊断方法在故障诊断领域逐渐成为主流[3]。文献[4]把随机森林（random forest，RF）运用到了轴承的故障处理上面，实验结果表明，与传统的分类器相比，随机森林的诊断正确率更高。

针对滚动轴承在发生故障时，由于故障振动信号具有非稳定性、非线性的特点，传统的诊断方法无法对故障特征进行自动提取，导致故障的分类正确率偏低。为了实现故障特征的自动提取从而提高故障识别率，本文提出了基于卷积神经网络（convolutional neural networks，CNN）与RF 相结合的算法模型解决了轴承故障分类问题。首先将轴承在不同工况下的振动信号转化为二维灰度图；然后再将灰度图输入到卷积神经网络中进行特征提取和学习；最后利用随机森林算法来进行分类。将识别结果与改进的残差网络，EEMD-CNN 不同的故障分类模型所得的结果进行对比，结果表明，本文所用的方法在轴承故障的准确率上更高。

1 故障识别的基础理论

1.1 信号转化为图像的方法

由于卷积神经网络在图像的特征提取方面表现出了强大的能力，所以，在将一维的原始数据输入到卷积神经网络之前，需要将其转化为图片的形式。比较常见的方法有傅里叶变换和小波分析，其本质就是将信号从时域转化为频域，然后再画频域图。但是，这些方法会增加数据处理的复杂度[5]。本文采用一种比较简单的方法，过程如下[6]：

首先从连续的原始时间序列信号中随机选取长度为n×n 点，组成矩阵M（n，n）。在对矩阵M 利用公式（1）进行归一化处理，得到一个像素为P（n，n）的灰度图。

式中：round 是取整函数。

使用该方法对轴承外圈的时域波形图进行转化的过程如图1 所示。

图1 振动信号转化为图片的过程Fig.1 Process of vibration signal transformation into picture

1.2 卷积神经网络

故障的特征提取在轴承的故障分类中是尤为重要的一部分，特征提取的好坏直接影响到分类效果。卷积神经网络作为一种前馈神经网络，通过卷积层的卷积操作可以对输入二维的特征信号自动进行特征提取。卷积神经网络的结构由输入层、卷积层、池化层、全连接层、输出层等组成。下面主要对卷积层、池化层、全连接层以及输出层作介绍[7]。

1.2.1 卷积层

卷积层利用卷积核对输入的数据进行特征提取，不同的卷积核通过卷积操作可以得到不同的特征图。卷积核是一个权值矩阵，大小通常为2×2，3×3，5×5 的矩阵。采用权值共享的机制，卷积核以一个固定的步长移动，同图像的像素值加权求和，再加上一个偏置，就会得到一个值。依次操作就会得到不同的值，将这些不同值按照顺序摆放，从而形成了特征图的矩阵。特征图的大小与上一层的输入矩阵、卷积核的个数和大小、移动的步长，填充方式padding 都有关。填充的方式可分为same 和valid。same 是在输入矩阵的周围填充零，使得原矩阵的边缘信息可以被有效地利用起来；valid 只进行有效的卷积，即对边界数据不进行处理。卷积运算的公式如式（2）所示[8]：

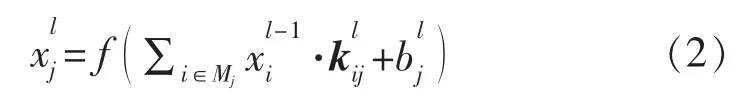
1.2.2 池化层

输入的数据经过卷积操作得到特征图之后，特征图将会输入到池化层，池化层又称为降采样层。添加池化层的主要目的是对输入的数据进行降维，减少网络的训练参数，而且还能对输入数据的特征进行进一步提取。池化操作主要分为最大池化和平均池化，一般采用最大池化。池化运算的公式如式（3）所示。

式中：down（）为采样函数。

1.2.3 全连接层和输出层

输入数据经过一系列卷积和池化操作之后，将提取到的特征扁平化为一维特征向量，然后再将其输入到全连接层中进行分类。输出层一般采用Softmax 层，将全连接层的分类结果归一化为一个概率分布，Soft max 层的输出值可以看成是对应样本的概率值。全连接层和Softmax 层的一般表达式为

式中：k 代表k 层网络；yk为全连接层的输出；wk为权重系数；xk-1为全连接层的输入；bk为偏置。

1.3 随机森林

随机森林是一种由许多决策树组合而成的分类模型。各个决策树之间是彼此独立的，在进行分类的时候，各决策树都会独立的对所输入的样本进行分类，最后会以投票的方式决定分类的结果。该算法的基本步骤如下[9]：

（1）利用Bootstrap 从原始样本中随机的采取k个样本，样本的数目要和原始样本的容量一样。

（2）利用这k 个样本分别建立k 个决策树模型。

（3）每个决策树模型输出一个结果，最后通过投票的方式对这k 个结果进行表决，从而确定最后的分类结果。

2 基于CNN-RF 的故障诊断模型

2.1 基本流程

滚动轴承在发生故障时，由于故障振动信号具有非稳定性、非线性的特点，传统的诊断方法无法对故障特征进行自动提取，导致故障的分类正确率偏低。为了实现故障特征的自动提取从而提高故障识别率，本文提出了一种基于CNN 与RF 相结合的滚动轴承故障识别的方法。该模型由数据的预处理、特征提取、RF 分类3 部分组成。卷积神经网络具有很好的特征提取能力，振动灰度图经过卷积神经网络的卷积和池化操作之后，可以很好的提取到灰度图的特征参数，RF 模型简单且不容易产生过拟合。因此，本文构建了CNN-RF 故障诊断模型，故障诊断的流程如图2 所示，此方法的步骤如下：

图2 故障识别流程Fig.2 Flow chart of fault identification

（1）获取轴承的振动信号；

（2）利用python 程序将轴承的振动信号转化为二维振动灰度图，并将其分为训练集和测试集；

（3）建立卷积神经结构并初始化参数，根据仿真结果来调整相应参数（例如卷积层数、激活函数、学习率等）；

（4）将图片输入到卷积神经网络，经过卷积和池化操作之后，得到了含有故障特征的数据集，在将数据集输入到flatten 层和全连接层扁平化为一维特征向量；

（5）将全连接层输出的一维特征向量输入到RF分类模型；

（6）为了使RF 模型的分类效果达到最优，需要用网格搜索对RF 中的不同参数进行调优；

（7）训练完成后，将测试集输入到最终的模型当中去进行分类。

3 实验与分析

3.1 实验说明

本实验基于Windows10 64 位操作系统，采用的是由Google 公司基于python 语言开发的Tensorflowgpu 框架，软件环境为Pycharm，处理器为Intel（R）Core（TM）i7-7700HQ@2.80 GHz×8，运行内存为8 GB，图像处理单元为NVIDIA GeForce GTX1050Ti。

3.2 实验数据描述

为了验证本文所提出的CNN-RF 有效性，利用来自于美国凯斯西储大学（case western reserve university，CWRU）的轴承数据进行仿真分析，采集来的数据来源于驱动端的振动信号，通过电火花技术人为引入故障，被测轴承为6205-2RS JEM SKF深沟球轴承，电机载荷为1 hp，采样频率为12 kHz，主轴转速为1772 r/min。考虑到实际工作中，轴承会出现不同情况的故障，即使在同一情况下，也会有不同程度的磨损。因此，实验数据要尽可能的全面描述轴承的不同故障。

数据包括了轴承在不同工况下的状态，分别为内圈故障、外圈故障、滚动体故障、正常状态，其中外圈故障采用的是以负荷区6 点钟方向为中心的6点钟方向的数据。故障直径表示轴承不同程度的磨损，包含0.18 mm，0.36 mm，0.54 mm。共计10 种工况，每种工况选取120000 个数据点，以1024 个数据点为一个样本，使用重叠采样对每种工况取1000个样本，一共有10000 个样本，训练集和测试集按照7∶3 进行划分。采用One-hot 编码对10 种工况样本数据进行标签化处理，实验数据集的详细情况如表1 所示。

表1 实验数据集Tab.1 Experimental data set

3.3 CNN-RF 模型参数的设计

本文设计的网络模型由特征提取层和分类层组成，具体设计如图3 所示的“卷积-卷积-池化-卷积-卷积-池化-卷积-卷积-池化-全连接-RF 分类器”的结构模型。其中，池化层采用最大池化方式。模型进行编译时，采用Adam 优化算法优化交叉熵损失函数，学习率为0.0001，迭代次数epochs 为50 次。模型结构的具体参数设置如表2 所示。

图3 CNN-RF 模型结构图Fig.3 Structure diagram of CNN-RF model

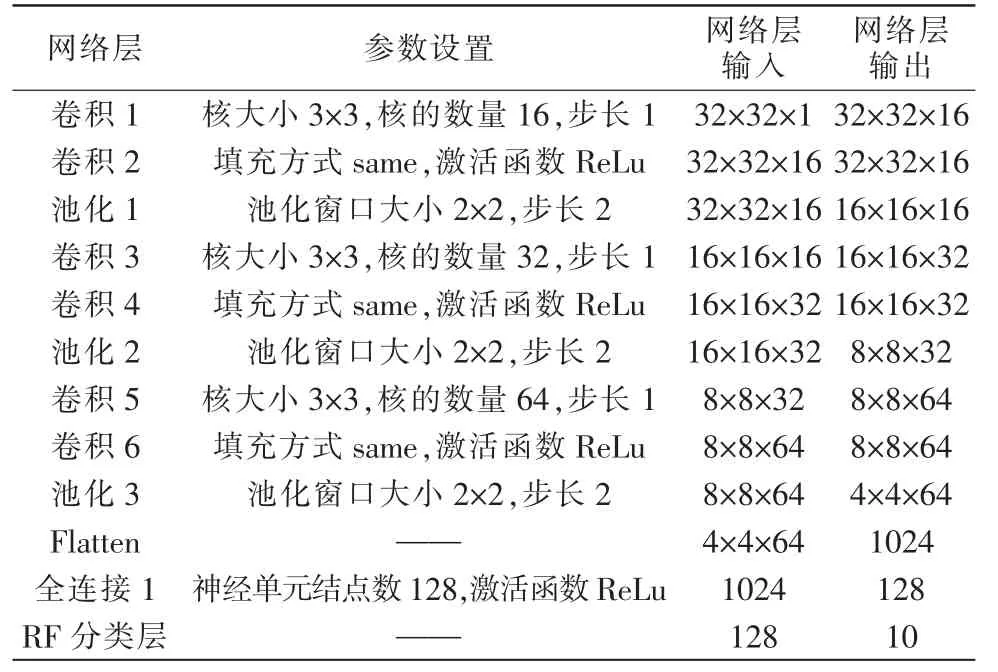
表2 模型参数Tab.2 Model parameter

3.4 实验数据的预处理

实验数据的预处理主要是把一维的振动信号用python 语言根据公式（1）将其转化为二维的振动灰度图，灰度图的格式为32×32×1，像素为32×32。由于文章篇幅有限，这里只取轴承在载荷为1 hp 下，故障直径为0 mm 的正常状态，故障直径为0.18 mm下的内圈故障、外圈故障、滚动体故障3 种情况做演示，其余情况均按照相同方法进行处理。轴承在这4种工况下的时域波形图和相对应的振动灰度图如图4 所示。

图4 振动信号时域波形图和灰度图Fig.4 Time domain waveform and grayscale image of vibration signal

3.5 实验结果与分析

将轴承在不同状态下的振动灰度图输入CNN中进行自适应特征提取，在将提取到的特征输入到RF 中进行分类。在RF 进行分类时，运用网格搜索对RF 的超参数进行优化选择，在优化的同时也进行交叉验证，交叉验证的次数选为5。优化的参数和范围如下所示：

决策树个数n_estimators∈［80，100，120］；最大特征数max_feature∈［3，5，7，9，11］；决策树最大深度max_depth∈［1，3，5，7，9，11，13］；节点可分的最小样本数min_samples_split ∈［100，120，150，180，200，300］；叶子节点含有的最少样本min_samples_leaf∈［10，20，30，40，50，100］。

为了评估CNN-RF 模型分类效果，采用精准率Precision、召回率Recall、F1-Score 值对模型进行综合评价[10]。

式中：TP 为预测和实际分类正确的数量；FP 为预测分类中错误的数量；FN 为实际分类错误的数量。

表3 展示了对轴承不同故障分类的精准率Precision、召回率Recall、F1-Score 值。其中，精准率平均值为0.999；召回率平均值为0.998；F1-Score 的平均值为0.998。

表3 CNN-RF 性能指标Tab.3 CNN-RF performance indicators

为了展示该模型对各类故障的分类效果，引入混淆矩阵对分类结果进行可视化，如图5 所示，本文所采用方法的诊断正确率可达99.79%。这表明该方法可以有效地对轴承的故障特征进行自适应提取，对故障类型进行精准分类。该模型的训练集和验证集准确率和损失率的变化曲线如图6 所示，从变化曲线可知，该模型的分类正确率高，并且没有出现拟合情况。

图5 CNN-RF 分类混淆矩阵Fig.5 CNN-RF classification confusion matrix

图6 CNN-RF 训练集和验证集准确率和损失率的变化曲线Fig.6 Change curve of accuracy and loss rate of CNN-RF training set and verification set

为了验证CNN-RF 的有效性，在相同的数据下与文献[11]、文献[12]进行比较。文献[11]采用的是改进的残差网络对轴承故障进行特征提取和分类，最后分类的正确率为95%。本文在对轴承的故障特征提取和故障分类方面采用的是不同的模型，进而提高了分类的正确率；文献[12]使用集合经验模态分解对轴承振动的信号进行分解，得到了若干个本征模态分量，根据相关指标选择适当的分量进行重构，将重构的特征向量输入到CNN 中进行故障诊断，分类的准确率可达96.7%。本文采用的是CNN 自适应的对轴承的故障特征进行提取和选择，无需人工干预，因此，准确率更高。

4 结语

针对滚动轴承在发生故障时，由于故障振动信号具有非稳定性、非线性的特点，传统的诊断方法无法对故障特征进行自动提取，导致故障的分类正确率偏低。本文提出了一种基于CNN-RF 相结合的滚动轴承故障识别的方法，利用CNN 可以直接从轴承的原始振动信号中进行特征提取，无需人工干预。然后，利用RF 进行分类。最后将识别结果与不同的故障诊断模型所得的结果进行对比，对比结果表明，本文所提出的方法在进行轴承的故障诊断上更具有优势，从而验证了该方法的有效性。