中小微企业的信贷决策模型*

周非凡，邱有昊，王旭东，林 韩

(南宁师范大学 计算机与信息工程学院，广西 南宁 530100)

0 引言

由于中小微企业规模相对较小，也缺少抵押资产，因此银行通常是依据信贷政策、企业的交易票据信息和上下游企业的影响力，向实力强、供求关系稳定的企业提供贷款，并可以对信誉高、信贷风险小的企业给予利率优惠。银行首先根据中小微企业的实力、信誉对其信贷风险做出评估，然后依据信贷风险等因素来确定是否放贷及贷款额度、利率和期限等信贷策略。

某银行对确定要放贷企业的贷款额度为10万～100万元；年利率为4%～15%；贷款期限为1年。附件1～3(2020年全国大学生数学建模竞赛C题附件数据，本文未列出附件)分别给出了123家有信贷记录企业的相关数据、302家无信贷记录企业的相关数据和贷款利率与客户流失率关系的2019年统计数据。该银行请你们团队根据实际和附件中的数据信息，通过建立数学模型研究对中小微企业的信贷策略，主要解决2个问题。

问题1： 对123家企业的信贷风险进行量化分析，给出该银行在年度信贷总额固定时对这些企业的信贷策略。

问题2：在问题1的基础上，对302家企业的信贷风险进行量化分析，并给出该银行在年度信贷总额为1亿元时对这些企业的信贷策略。

1 模型假设与问题分析

1.1 模型假设

(1)假设企业信誉等级过低，银行不同意该企业贷款；

(2)假设分配给最高年利率的企业的信贷总额为100万元。

1.2 问题分析

针对问题1，要得出该银行在年度信贷总额固定时对中小微企业的信贷策略模型，首先对这些企业进行信贷风险量化分析，然后根据各信誉等级与企业数据的相关性，建立数学模型。

针对问题2，要得出该银行在信贷总额为1亿元时对企业的信贷策略，首先根据建立的信誉评价模型，对附件2(未列出)的数据进行信誉等级划分，其次在信誉评价模型下分析附件2(未列出)中各信誉等级公司相关数据与附件1(未列出)得到结论的一致性。最后代入数值信贷总额1亿元，分析各种方案结果，并选择最优的决策方案。

2 模型的建立和求解

2.1 问题1模型的建立和求解

2.1.1 量化分析

分析1:对违约率进行分析

违约率=违约数/记录总数，对附件1(未列出)数据进行处理分析可得到信誉等级与违约率有直接联系，随着信誉等级从A至D下降，违约率从低到高增长。所以信誉等级与违约率成指数增长，违约率越低，信誉等级越高。

分析2:对进项发票作废率与信誉等级进行分析

进项发票作废率=进项废票总数/进项发票总数,附件(未列出)分析可知，进项发票作废率与信誉等级成上凸关系，A、D信誉等级废票率较低，B、C信誉等级废票率较高。大致估计A、D信誉等级企业退单、退款的可能性较低。

分析3:对销项发票作废率与信誉等级进行分析

销项发票作废率=销项废票总数/销项发票总数,附件1(未列出)分析可知，销项发票作废率与信誉等级成下凹关系，A、D等级销项废票率较高，B、C等级销项废票率较低。分析得知A、D信誉等级企业的退单、退款率较高。

分析4:对信誉等级与盈利率关系的分析

信誉等级交易金额平均值=等级总金额/等级交易次数,由附件1(未列出)分析可知各等级销项金额均比进项金额高，企业基本处于盈利状态。随着信誉等级的降低，企业进项与销项金额也处于下降状态。进一步分析可知，虽然A等级企业所涉及的金额巨大，但是盈利率并不如B,C,D等级的盈利率高。

分析5:对信誉等级与交易税额的分析

信誉评级交易税额平均值=评级总税额/评级交易次数,通过附件1(未列出)数据计算得出表1、表2数据。表中增值税S=税率×(销项金额-进项金额)，税率=税额/金额。

表1 各信誉等级与进、销项税率的关系

表2 各信誉等级与增值税的关系

分析得出，随着信誉等级的降低，进项税率趋于缓和，销项税率呈“降->升->降”状态。增值税与信誉评级成抛物线关系，税率对信誉评级的影响并不大，未起到决定性因素。

分析6:信誉等级方差量化分析

计算A、B、C信誉等级在2016—2020年的进项、销项金额平均数和对应方差，以及D信誉等级在2017—2020年的进项、销项金额平均数和对应方差。根据样本方差式[3]：

(1)

得到各等级企业平均方差，分析得出信誉等级与销项方差无明显关联，信誉等级与进项方差成正相关。

分析7：不同信誉等级企业年进项金额与销项金额相关性分析

根据分析6并结合皮尔逊相关系数式[4]：

(2)

得出A、B、C信誉等级在2016—2020年以及D信誉等级在2017—2020年的进项金额平均数和每年销项金额平均数的相关系数R，表3。

表3 各信誉等级对应的相关系数

由分析7得到，相关系数与信誉等级有极强的相关性。

综上所述，信誉等级受到企业的进项平均金额、销项平均金额、进项总和、销项总和、进项发票有效率和销项发票有效率等因素的影响。

2.1.2 确立决策模型

通过2.1.1的量化分析，确定影响信誉评级的因素。根据这些影响因素建立信贷决策模型，使银行盈利最大。

(1)由附件1(未列出)统计得出各信誉评级企业的违约率(表4)。

表4 各信誉等级对应的违约率

根据违约率做出决定，信誉评级为D的企业不予以贷款，该信誉等级企业必然违约，如果银行贷款给D信誉企业必然会有亏损。下面建立模型过程中，不考虑信誉等级为D的企业。

(2)建立决策树模型

信誉评级A、B、C违约损失率s1、s2、s3分别为0%、2.6%、5.8%。因为放贷企业的贷款额度为10万～100万元，统计得出123家企业中有27家为A级，38家为B级，34家为C级。故A级信誉公司的贷款上限金额为2700万元，B级信誉公司的贷款上限金额为3800万元，C级信誉公司的贷款上限金额为3400万元。设Q0为固定信贷总额，D1为银行纯利息，D2为银行违约损失额，D3为银行潜在流失额。a，b，c分别为等级A，B，C所占信贷总额比率。qk(k=A,B,C)为等级k的贷款年利率，Lk(k=A,B,C)为等级k的客户流失率。

计算得到银行的利润为:

D1=Q0×a×qA+Q0×b×qB+Q0×c×qC

(3)

D2=s1×Q0×a×qA+s2×Q0×b×qB+s3×Q0×c×qC

(4)

D3=LA×Q0×a×qA+LB×Q0×b×qB+LC×Q0×c×qC

(5)

由式(3)(4)(5)建立最大目标函数为：

maxZ=D1-D2-D3

(6)

约束条件：

(7)

根据纯利息、违约损失额、潜在损失额得到银行所得真实利润为：

Z=Q0×a×qA(1-s1-LA)+Q0bqB(1-s2-LB)+Q0×c×qC(1-s3-LC)

(8)

因为违约损失率:s1、s2、s3分别为0%、2.6%、5.8%，所以，

Z=Q0×a×qA(1-LA)+Q0×b×qB(0.9740-LB)+Q0×c×qC(0.9420-LC)

(9)

根据附件三，qA、qB、qC在0.04～0.15之间变化，就对应LA、LB、LC的变化，所以Z随着a、b、c、LA、LB、LC的变化而改变。a+b+c=1利用控制变量法控制a、b、c不变，再根据实际年利率算式:q(1-s-L)及附件3的数据使用枚举法[1]得出最高实际年利率。计算得到A、B、C信誉等级理论与实际的贷款年利率表，表5。

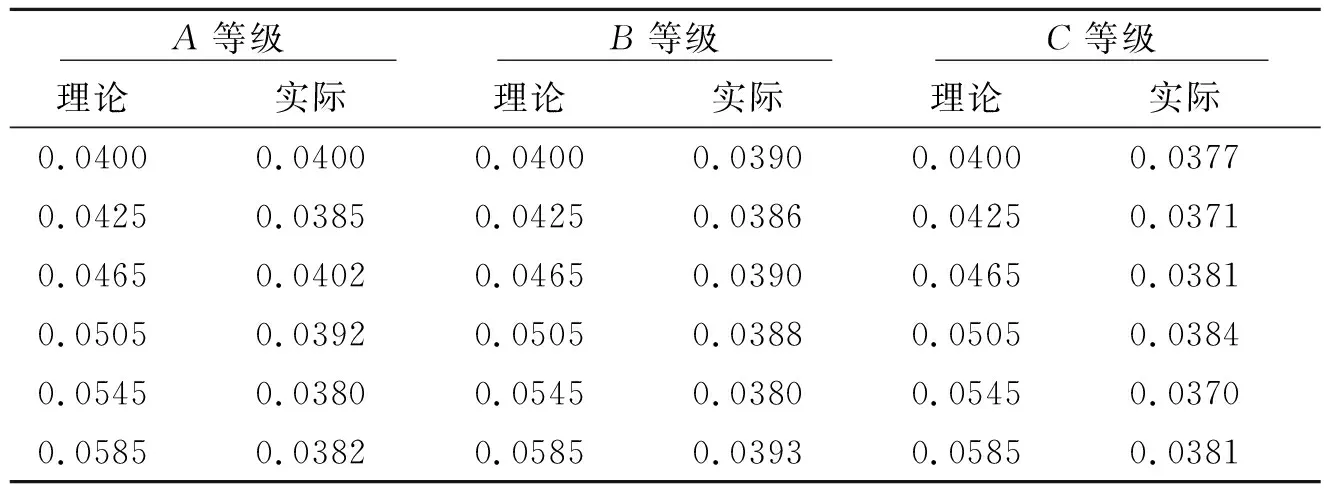
表5 A，B，C信誉等级理论贷款年利率与实际贷款年利率

统计可得对信誉等级为A的企业来说，贷款年利率为0.0465时，银行所得实际年利率最大，为0.040 2，B、C信誉评级企业类似表5中红色标出。各信誉评级实际年利率的最优值，见表6。

表6 各信誉评级年利率的最优值

根据表6，最大目标函数为Z：

maxZ=Q0×a×pA+Q0×b×pB+Q0×c×pC

(10)

(11)

因为年度信贷总额固定值Q0未确定，为得出Z(Zj表示第j种方案所得的最高收益，j=1,2,3,4)，做出如下讨论。

(1)若年度信贷总额小于2700万元时，银行选择的最优方案是所有信贷给A等级企业，即a为1(100%)，b、c为0(0%)即银行所得最高收益为：

Z1=Q0×0.0402

(2)若年度信贷总额大于2700万元小于6500万元时，银行选择的最优方案是2700万元信贷给A等级企业，剩余的给B等级企业，即a为2700/Q0，b为(Q0-2700)/Q0，c为0(0%)，即银行所得最高收益为：

Z2=2700×0.040188686+(Q0-2700)×0.0393

(3)度信贷总额大于6500万元小于9900万元时，银行选择的最优方案是2700万元信贷给A等级企业，3800万元信贷给B等级企业，剩余的信贷给C等级企业，即a为2700/Q0，b为3800/Q0，c为(Q0-6500)/Q0，即银行所得最高收益为：

Z3=2700×0.0402+3800×0.0393+(Q0-6500)×0.0384

(4)信贷总额大于9900万元时，银行选择的最优方案是2700万元信贷给A等级企业，3800万元信贷给B等级企业，3400万元信贷给C等级企业，即a为2700/Q0，b为3800/Q0，c为3400/Q0。即银行所得最高收益为：

Z4=2700×0.0402+3800×0.0393+3400×0.0384

银行在年度信贷总额固定时，A对123家企业的信贷策略：

A等级企业信贷年利率为0.0645时，银行的实际最高年利率为0.0402；B等级企业的信贷年利率为0.0585时，银行的实际最高年利率为0.0393；C等级企业的信贷年利率为0.0505时，银行的实际最高年利率为0.0384。银行最高利润Z：

maxZ=Zi(i=1,2,3,4)

i代表不同的方案，根据Q0的范围确定i，银行得到最高收益。

假设信贷最高额度分配每家企业100万元，由以上模型分析得出的结果做出不确定型决策树[2]，如图1所示。

图1 不确定型决策树

综上所得：在银行年度信贷总额固定时，根据金额的范围选择对应的方案与决策树分支，得到最优信贷策略及其最优利润。

2.2 问题二的分析与求解

2.2.1 建立信誉评价模型

在问题一的基础上，根据评价指标建立信誉评级分类模型对企业进行分类[5]。设信誉评级A大于u1指标，信誉评级B小于u1大于u2指标，信誉评级C小于u2大于u3指标，信誉评级D小于u3指标。a1为进项平均金额，a2为销项平均金额，a3为进项总和，a4为销项总和，a5为进项发票有效率，a6为销项发票有效率，xNi(i=1,…,6)表示信誉评级N(N=A,B,C,D)对应的企业的进项平均金额、销项平均金额、进项总和、销项总和、进项发票有效率、销项发票有效率。fN为信誉等级N对应的四个指标区间，根建立整体目标函数：

a1xNi+a2xNi+a3xNi+a4xNi+a5xNi+a6xNi=fN(A,B,C,D)

(12)

A信誉等级函数及约束条件：

s.t.a1xAi+a2xAi+a3xAi+a4xAi+a5xAi+a6xAi≥u1

(13)

B信誉等级函数及约束条件：

(14)

C信誉等级函数及约束条件：

(15)

D信誉等级函数及约束条件：

s.t.a1xDi+a2xDi+a3xDi+a4xDi+a5xDi+a6xDi≤u3

(12)

将附件1中各个等级企业的数据代入相应的函数中，拟合出各因素的相关系数及其指标。用MATLAB进行拟合，拟合的相关结果见表7，表8。

表7 信誉评级指标

表8 因素相关系数

根据表7，8所得数据建立信誉评级分类[6]模型，即建立目标函数：

fN(A,B,C,D)=

(1.0633xNi-15.2206xNi-16.4330xNi+12.0427xNi+139.9022xNi-49.3159xNi)

(17)

(18)

依据模型结果，做出决策树，如图2所示。

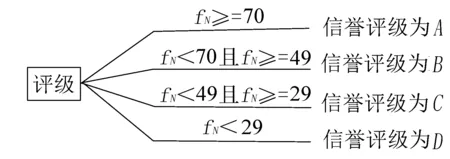
图2 信誉评价决策树

按照本节的结果，对附录2的企业进行信誉等级划分，可以得到各个企业的信誉等级。

2.2.2 量化分析

对附件2中已经信誉评级的企业进行量化分析。

(1)发票作废率分析

分析得出A与C信誉评级企业的销项发票率较高，相反B,D信誉评级的销项发票率较低。与问题一的结果进行比较，A,B信誉评级企业的销项废票率基本一致，C,D信誉评级企业数据略有不同。而进项废票率B,C,D基本一致，而A有所不同。由此可知计算所得的信誉评级废票率基本上与附件1中的各级信誉评级的一致。

(2)进项、销项金额分析

各等级企业进项金额基本一致，而销项金额有着较大的差异，信誉等级与销项金额成正相关，与问题一分析得出的结果基本一致，在A与B评级之间，有着较大的落差，而在B,C等级之间，销项金额的浮动并不大，而进项金额与问题一分析得出的结果基本一致。

(3)平均税额及相关增值税分析

数据分析得到增值税与销项税额是成正比，且各等级企业间进项平均税额基本一致，由此说明金额与税额之间的税率基本一致，各等级企业税额率相差并不大。与问题一分析得出结果比较，销项税额都是起伏较大的，且各等级之间的进项税额，增值税变化趋势大体一致。然而，D等级企业平均增值税为负，该等级企业平均下来是亏损的，这势必会成为银行评定信誉等级的标准。

综上所述，由建立的模型对附录2进行评级，得到的各信誉等级影响因素，极大吻合了附件1中评级企业的数据趋势、规律。有效验证了评级模型的稳定性，可靠性，有效性。

2.2.3 确立决策模型

由评级模型划分后，统计各信誉评级的企业数量(根据提示及相关说明在此信誉评级D不做信贷这里就不在统计)。302家企业各评级数量(表9)。

表9 302家企业各等级数量表

假设各信誉评级的违约率与附件1中所给的违约率相同，根据附件3所给的年利率与客户流失率的对应关系，将等级企业数量带入第一问的模型中，计算求出银行分配信贷后得到的最优收益。即：信贷总额为10000万元，因为放贷企业的贷款额度为10万～100万元，假设所得的利息最大,企业的信贷额是100万元，银行获得收益率最大化。已统计出302家企业中有31家是A等级，42家是B等级，109家是C等级。因此A级公司的贷款上限金额为3100万元(QA)，B级公司的贷款上限金额为4200万元(QB)，C级公司的贷款上限金额为10900万元(QC)。

计算银行此时所得到的利润，由式(3),(4),(5)可以得到银行最大利润的模型为：

maxZ=D1-D2-D3

(19)

(20)

根据纯利息、违约损失额、潜在损失额得到银行所得利润：

Z=10000×a×qA(1-s1-LA)+10000×b×qB(1-s2-LB)+10000×c×qC×(1-s3-LC)

其中qN(1-si-LN)为银行实际所得的年利率，其值可用wN来表示。因为信誉等级A、B、C违约损失率s1、s2、s3分别为0%、2.6%、5.8%，所以有:

Z=10000×a×qA(1-LA)+10000×b×qB(0.974-LB)+10000×c×qC(0.9420-LC)

根据年利率的变化、对应的客户流失率及违约率，对附件3的数据利用枚举法[1]得出最高利率W(W=A,B,C)。各信誉等级的最优年利率,见表10。

表10 各信誉等级的最优年利率

对问题一所得到的决策树做出决定，决策树如图3所示。

图3 问题二决策树

具体各分支及各方案内容如下：

(1)若年度信贷总额小于3100万元时，银行选择的最优方案为：所有信贷给A等级企业，即a为1(100%)，b为0(0%)，c为0(0%)，即银行所得最高收益为：

Z1=Q×0.0402

(2)若年度信贷总额大于3100万元小于7300万元时，银行选择的最优方案为：3100万元信贷给A等级企业，剩余的给B等级企业，即a为3100/Q，b为(Q-3100)/Q，c为0(0%)，即银行所得最高收益为：

Z2=3100×0.0402+(Q-3100)×0.0393

(3)若年度信贷总额大于7300万元小于18200万元时，银行选择的最优方案为：3100万元信贷给A等级企业，4200万元信贷给B等级企业，剩余的信贷给C等级企业，即a为3100/Q，b为4200/Q，c为(Q-7300)/Q，即银行所得最高收益为：

(4)若年度信贷总额Q大于18200万元时，银行选择的最优方案为：3100万元信贷给A等级企业，4200万元信贷给B等级企业，10900万元信贷给C等级企业，即a为3100/Q，b为4200/Q，c为10900/Q。

在信贷一亿元时，根据决策树及方案明细可知，最优策略应选择决策树第三分支及第三方案，所得结果如下：

Zmax=(3100×0.0402+4200×0.0393+(104-7300)×0.0384)=393.2062

综上，固定信贷额为一亿元时，最优策略为，设置信誉A级企业的年利率为0.0465，设置信誉B级企业的年利率为0.0585，设置信誉C级企业的年利率为0.0505，制定信誉A级的企业占总信贷额31%，信誉B级的总企业占42%，信誉C级的总企业占27%，银行所得的年利润最高为393.2062万元。

4结语

利用皮尔逊相关系数，分析各个因素之间的关系，从中寻找建模思路。根据显著性因素建立了线性规划模型，并求得相应的最佳结果。因为数据较少，得到的参数不够准确，模型稳定性有欠缺。