具有饱和发生率和恢复率的潜伏期时滞SEIR模型*

陈桦剑,韦煜明

(广西师范大学 数学与统计学院，广西 桂林 541006)

1 引言

时滞效应在传染病传播过程中扮演着重要的角色，具有时滞效应的传染病动力学模型能更准确地描述传染病的传播机制，传染病的潜伏期可以用时滞模拟,因此，许多学者开始研究具有时滞效应的传染病模型[8，9，10].

受到上述文献，以及文献[11,12]的启发，本文综合考虑潜伏期时滞对具有饱和发生率和恢复率的SEIR 传染病动力学模型的影响，提出一个具有饱和发生率和恢复率的潜伏期时滞SEIR模型，讨论模型平衡点的存在性.通过构建李雅普诺夫函数，利用LaSalle不变集原理和Hurwitz定理讨论模型的平衡点稳定性，指出：当R0≤1时，模型的无病平衡点全局渐近稳定；当R0>1时，地方病平衡点局部渐近稳定.

2 模型

考虑以下时滞微分方程系统：

(1)

(H2) 当I≥0时，g″(I)≤0且g′(I)≥0.

假设系统(1)满足初始条件：

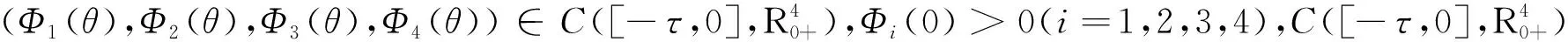
由于系统(1)中第一、第三、第四个方程不含E，故研究系统(1)可以转化为研究下列系统：

(2)

3 解的非负性和有界性

引理1在初始条件S(0)>0，I(0)≥0，R(0)≥0下，系统(2)的解始终非负有界.

证明非负性[13]用反证法.假设存在最小的时间t1>0，使得S(t1)=0，则将其代入系统(2)中的第一个方程可得

S′(t1)=Λ>0,

于是存在一个充分小的ε，使得在(t1-ε,t1)上有S(t)<0，这与在(0,t1)上S(t)>0矛盾.

假设存在最小的时间t2>0，使得I(t2)=0，则将其代入系统(2)中的第二个方程可得

I′(t2)=e-μτS(t2-τ)g(I(t2-τ))≥0,

于是存在一个充分小的ε，使得在(t2-ε,t2)上有I(t)<0，这与在(0,t2)上I(t)>0矛盾.

由系统(2)第三个方程可得

再由比较定理得出R(t)≥R(0)e-μτ≥0,因此，非负性得证.

有界性因为N(t)=S(t)+E(t)+I(t)+R(t)，所以

因此，

4 基本再生数和平衡点

基本再生数是刻画传染病发病初期疾病传播状况的一个重要阈值，是区分疾病是否消亡的重要指标，它表示在一个全部是易感者的人群中进入一个染病者，在其平均患病周期内所能传染的人数[14].

本节将研究系统(2)的基本再生数和平衡点的存在性.利用文献[15]中介绍的下一代矩阵方法，可得系统(2)的基本再生数

根据系统 (2) 第一和第三个方程可得

AI2+BI+C=0,

(3)

其中，

显然A>0，当基本再生数R0>1时，C<0，此时，式(3)中判别式Δ=B2-4AC>0，存在唯一的地方病平衡点E2(S*,I*，R*)，其中

5 稳定性分析

系统(2)的Jacobian矩阵为

系统(2)的特征多项式为

f(λ)=λ3+a1λ2+a2λ+a3+(b1λ2+b2λ+b3)e-λτ,

其中

b1=-e-μτg′(I)S，

b2=-e-μτg′(I)S(2μ+g(I)-g(I(t-τ)))，

b3=-e-μτg′(I)S(μ(μ+g(I))-μg(I(t-τ))).

5.1 无病平衡点的局部稳定性

定理1当R0<1时，系统(2)的无病平衡点E1是局部渐近稳定的.

证明系统(2)在无病平衡点E1处的特征方程为

故特征值满足

综上，当R0<1时，系统(2)的无病平衡点E1是局部渐近稳定的.

5.2 无病平衡点的全局稳定性

定理2当R0≤1时，系统(2)的无病平衡点E1是全局渐近稳定的.

证明令

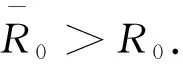
则有

从而可得

5.3 地方病平衡点的局部稳定性

定理3当R0>1时，地方病平衡点E2是局部渐近稳定的.

证明在地方病平衡点E2处，系统(2)的Jacobian矩阵为

对于τ∈[0,+∞)，系统(2)的特征方程为

f(λ)=λ3+a1λ2+a2λ+a3+(b1λ2+b2λ+b3)e-λτ=0.

在系统(2)中，地方病平衡点E2满足

当λ=0时，

故此时，f(λ)无零根.

当时刻τ=0时，

f1(λ)=λ3+(a1+b1)λ2+(a2+b2)λ+(a3+b3)，

其中

2μ+g(I*)+e-μτS*g′(I*)-e-μτS*g′(I*)=2μ+g(I*)>0,

a2+b2=(2μ+g(I*))e-μτS*g′(I*)-e-μτS*g′(I*)(2μ+g(I*)-

g(I*))+μ(μ+g(I*))=e-μτS*g′(I*)g(I*)+μ(μ+g(I*))>0,

a3+b3>0.

因此，τ=0时，f1(λ)有非负实部，于是根据Hurwitz判别法，有结论：对于τ=0，当R0>1时，地方病平衡点E2是局部渐近稳定的.

当τ>0时，假设λ=wi(w>0)是f(λ)=0的一个根，则有

-w3i-a1w2+a2wi+a3+(-b1w2+b2wi+b3)(coswi-isinwi)=0，

分离实部和虚部可得

(b1w2-b3)sinwi+b2wcoswi=w3-a2w，

(4)

b2wsinwi-(b1w2-b3)coswi=a1w2-a3，

(5)

将(4)、(5)两式分别两边平方后相加，可得

w6+pw4+qw2+v=0.

令w2=z，则有f2(z)=z3+pz2+qz+v,其中

(μ(μ+g(I*)))2=(e-μτS*g′(I*))2g2(I*)+(μ(μ+g(I*)))2>0,

因此，f(λ)不存在纯虚根.所以τ>0时，f2(z)有非负实部，于是根据Hurwitz判别法，得到结论：对于τ>0，当R0>1时，地方病平衡点E2是局部渐近稳定的.

综上，当R0>1时，地方病平衡点E2是局部渐近稳定的.

6 结论

本文提出了具有饱和发生率和恢复率的潜伏期时滞SEIR模型，证明了当R0≤1时，系统(2)的无病平衡点E1全局渐近稳定，说明随着时间的流逝，染病者逐渐减少，慢慢消失，未在大范围内传播及造成消极影响；当R0>1时，地方病平衡点E2在区域内局部渐近稳定，说明随着时间的流逝，如果未对传染病传播进行干预，则染病者人数逐渐稳定，且染病者长期存在.