基于动态C藤pair-Copula的电力系统动态经济调度场景协同优化算法
宁楠,范俊秋,徐潘宇驰,程培军,林盛振,谢敏
(1.贵州电网有限责任公司贵安供电局,贵州 贵安 550003;2.广东电网有限责任公司天河供电局,广东 广州 510075 3.华南理工大学,广东 广州 510640)
高比例新能源并入的电力系统具有良好的应用前景[1]。与此同时,新能源自身固有的波动性、随机性和间歇性[2]等特点,也为电力系统的安全经济调度过程带来了复杂的不确定性冲击。为了准确应对高维新能源并网后引入的调度风险问题,有必要对高维新能源发电的相关性建模以及相应的系统动态经济调度问题进行研究[3-6]。
随着新能源的并网容量进一步增长,多个新能源电场基于可再生能源类型特点、所处地理位置和气象因素的相似性[7],存在高维变量出力相关性较强的特征。Copula函数在新能源出力建模中得到了广泛的应用[8-11]。但是,当系统中接入的新能源维度增加时,单一的Copula函数难以对高维变量展开建模分析。藤结构的pair-Copula模型[12-13]使用二元Copula函数作为基础,根据多种逐层合并的方式,对应形成多元Copula的联合分布函数,能够有效提高建模的准确性。
为顺利求解含高维新能源的动态经济调度问题,已有研究通常引入随机规划理论,从而解决经济调度模型中新能源出力的间歇、波动以及随机问题[14]。典型方案有机会约束规划法[15-17]、场景分析法[18-20]等。以场景分析为基础的随机规划模型,主要将抽样生成的若干误差场景作为纽带,不断使随机优化向确定优化进行转换[21-22],但其应用的有效性受限于场景数量的选择。分布式优化技术通过合理分解建立在场景分析基础上的经济调度问题,尽可能全面地考虑了各个场景的贡献[23]。但是,已有研究中对于高维新能源间的出力相关性考虑不够精细。
针对以上研究存在的不足,本文首先基于动态C藤pair-Copula理论建立模型,能够准确描述高维新能源间的出力相关特性。然后,基于场景分析与多学科协同优化的思想,设计及求解含高维新能源的动态经济调度场景协同优化模型,从而有效提升引入高维相依新能源的协同优化经济调度的计算效率。
1 基于动态C藤pair-Copula的高维新能源出力建模及场景生成方法
为充分考虑并网新能源发电机组的随机特性给系统运行产生的影响,本文基于动态C藤pair-Copula函数,形成高维新能源的联合出力分布模型,并通过抽样技术完成各新能源出力随机误差场景生成过程。
Copula思想与模型以其灵活、实用的特性得到金融分析建模以及随机新能源相关性分析等领域的广泛关注与使用。Copula技术通过整合多维变量的边缘分布函数,以及与之相适应的单个Copula函数,能够方便地获得其联合分布数学模型进行模拟。为确保高维变量之间的相依特性获得更加精确的刻画,pair-Copula函数在单纯的Copula建模思想基础上,进一步对高维变量进行精细化建模。pair-Copula以二元Copula分布为基础,采取逐层合并的方式来构造多元高维Copula联合分布函数。图1给出了pair-Copula函数的两种常用结构图,即C-vine(C藤)和D-vine(D藤)。该方法能够引入多类型的Copula分布,有效提升模型的适用性和异构性[24]。假若存在与其他所有新能源发电均具有较强相关性的电源,则适宜采用C藤结构,否则应采用D藤结构。

图1 基于pair-Copula方法的两种藤Copula结构
侧重于研究的实际性,本文通过对五类常用的静态Copula函数以及三类动态Copula函数加以有机结合,构建基于C藤pair-Copula函数的高维新能源出力动态模型。文中模型采用的三类动态Copula函数分别是时变gaussian Copula函数、时变t-Copula函数与时变clayton Copula函数[25-26]。动态Copula函数的时变性,指的是其表达式中具备相应的时变参数。具体公式如下所示:
时变gaussian Copula函数的参数:
(1)
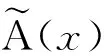
时变t-Copula函数的参数:
(2)

时变clayton Copula函数的参数:
(3)
式(3)中,ρct为时变clayton Copula函数的时变参数,ωρc、βρc、αρc为ρct的相关系数。
1.1 高维新能源的出力相关性建模
建立n维新能源出力相关性模型的具体流程如下:
Step 1:求取n维原始变量的边缘分布函数。首先,读取多个新能源电场的历史出力数据X,并进行相应的标幺化;其次,利用核密度估计法,求出边缘概率分布F(x);最后,基于各变量间的线性相关系数由大及小的顺序原则,重新排列这n个随机变量,并记排序后的随机变量为{x1,x2,…,xn},x1即为根节点。同时,令ui=Fi(xi)。
Step 2:选取最优Copula函数。利用与经验Copula函数的欧氏距离最小,对该层根节点与其余节点间的Copula函数进行选取;此外,相应的Copula参数将基于极大似然函数法求得。
Step 3:求取下一层节点的pair-Copula序列。通过结合该层节点的序列,以及下一层节点的最优Copula函数,从而根据式(4)求取下层各节点pair-Copula序列。
(4)
式(4)中,Ci,j|k为二元Copula分布函数。此外,vj代表向量v中的第j个变量,v-j代表向量v去掉vj后的向量。
Step 4:重复Step 2和Step 3,直至最后一层节点的建模结束,即完成了描述n维新能源出力相关性的高维动态模型构建。
1.2 基于动态C藤pair-Copula的场景采样分析方法
基于场景采样分析技术,对动态C藤pair-Copula模型展开采样,具体过程如下:
Step 1:生成n个不仅服从[0,1]均匀分布,而且各自独立的随机数wi(i=1,2,…n);
Step 2:设n维采样序列为{x1,x2,…,xn},令w1=x1,w2=F(x2|x1),…,wn=F(xn|x1,…,xn-1),根据式(5)求取n维采样序列。
(5)
基于上述过程对新能源出力的高维动态模型进行采样,获得采样结果后,在场景削减的过程中引入基于概率距离的快速前代消除思想,有助于后续完整模型的构建。
2 考虑高维新能源相依性的电力系统动态经济调度模型
2.1 目标函数
为了保证电网调度结果能够在安全稳定运行的情况下兼顾节能环保问题,以发电总燃耗成本与废气排放成本之和最小建立目标函数。
minF=F1+F2
(6)
式中,F为系统的总运行成本,F1为系统的燃油消耗成本,F2为系统的废气排放成本;A2,i、A1,i、A0,i表示常规机组i的燃油消耗成本系数;PGi(t)代表常规机组i在时段t内的有功功率;Cp代表常规机组废气排放的环保处理单价;B2,i、B1,i、B0,1代表常规机组i的废气排放系数;T代表调度周期,取为24h;N表示常规机组数量。
2.2 约束条件
模型的约束条件如式(7)至式(12)所示。
(7)
式(7)为系统运行中的功率平衡约束。其中PRj(t)表示新能源发电机组j在时段t内的有功功率;PLoad(t)表示系统在第t时段的负荷总和;s为场景区分标志,预测场景下有s=0,随机误差场景下则为s≠0;Nr为新能源发电机组的数量。
(8)
(9)
式(8)为系统运行中的向上、向下旋转备用约束,式(9)为常规机组出力的上限、下限约束。式中,PGi,max、PGi,min分别代表常规机组i出力的上限以及下限;α表示负荷预测偏差率,一般取5%~10%。
(10)
式(10)为系统运行中的机组出力爬坡约束。式中,rui、rdi分别代表常规机组i向上、向下出力爬坡率,ΔT表示单位调度时段。
(11)
式(11)为系统运行中的线路有功潮流约束。式中,Pmn(t)为以节点m、n为两个端点的输电线路mn在时段t内的有功功率;Pmn,max为输电线路mn的有功功率最大限制值;kl表示关键输电断面k所包含的线路条数;Pk,j(t)为在时段t内,关键输电断面k内的第j条线路所输送的有功功率;Pcut,max(k)表示关键输电断面k的有功潮流最大限制值。
(12)
式(12)为系统运行中的场景功率转移约束。式中,ΔPGi(t)为该场景内的常规机组i于时段t的可转移功率;Ghyd为水电机组集合,Ei,hyd为第i台水电机组的水电量日最大限制值;Ggas为燃气机组集合,Ei,gas为第i台燃气机组的气电量日最大限制值。
3 基于场景分析的电力系统动态经济调度多学科协同优化算法
多学科协同优化方法充分融合吸收了分布式优化技术以及二级优化技术的核心思想[27-28],能够针对性地为具有高维特征的模型设计高效的多级优化框架,从而将高维、复杂的原始模型解耦成相对低维、简化的优化模型,高效地降低了原始模型的求解难度,也顺利解决了“维数灾”等难题,是求解复杂系统优化问题的有力工具。其本质在于,按照适应于实际复杂系统优化问题的标准对原模型进行合理分解,从而简化原模型,获得单独的主优化问题和部分相对简单的子优化问题,并在主优化级对所有子优化问题的最优解进行场景分析与优化调整,最终求得原始模型的最优解。
3.1 基于多学科协同优化的高维场景解耦动态经
济调度模型
具体的建模展开如下:
(1)主优化级模型
主优化级模型的目标函数,即为式(6)中原系统级模型的目标函数。主优化级模型的约束条件不仅涵盖式(7)至式(12)中所有只涉及预测场景的部分,还包含主优化级的一致性约束,如式(13)所示:
(13)

(2)子优化级模型
(14)
s.t.式(7),s≠0
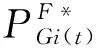
如上所述,基于MCO技术与场景分析方法的高维场景解耦动态经济调度模型建模计算框架如图2所示。

图2 基于MCO的高维场景解耦动态经济调度模型计算结构Fig.2 Computational structure of high-dimensional scene decoupling dynamic economic dispatch model based on MCO
3.2 基于动态C藤pair-Copula建模的高维新能源电网动态经济调度求解步骤
基于动态C藤pair-Copula函数对高维新能源进行建模,并结合场景分析法与多学科协同优化方法对电网动态经济调度问题展开求解。求解步骤流程如图3所示,详细描述如下:
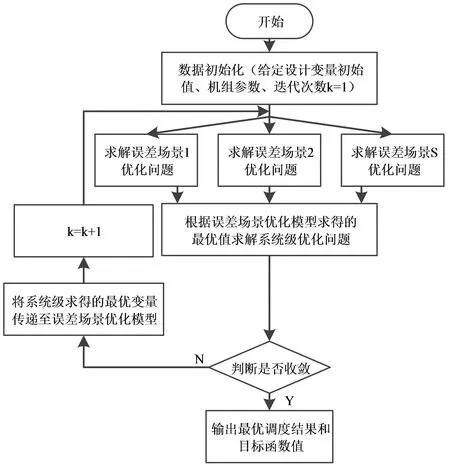
图3 基于场景分析的电网动态经济调度多学科协同优化算法流程图Fig.3 Flow chart of multidisciplinary collaborative optimization algorithm for power grid dynamic economic dispatch based on scenario analysis
Step 1:主优化级模型进行数据初始化,并传送到子优化级模型,同时令迭代次数k=1。
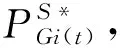

|(F(k+1)-F(k))/F(k+1)|≤ε
(15)
式(15)中,F(k)、F(k+1)为第k次以及第k+1次迭代求解得到的主优化级模型目标函数值;ε为迭代收敛的精度,设置为10-3。
4 算例分析
4.1 仿真系统
仿真系统采用标准IEEE 118节点系统进行建模分析。选择10个装机容量均为75MW的实际风力发电场Wi(i=1,2,…,10),并且所有风电场全部落在美国加利福尼亚州的某一片区中。风电场接入原仿真系统发电机节点位置的对应关系如表1所示。

表1 风电场接入系统位置对应关系Tab.1 Position correspondence of wind farm access system
另外,电力系统在调度当日的最大负荷为6000MW,电网负荷预测偏差率α为5%。如图4所示,为部分风力发电场的预测出力曲线。可以看到,在高维新能源接入系统的情景下,其功率输出的相关关系复杂性较高。

图4 部分风电场的预测出力曲线Fig.4 Predictive outputs curves of partial wind farms
4.1.1 高维新能源的出力相关性建模
基于1.2节中的建模流程,取采样时长为1年、采样间隔为15分钟,以获得10个风电场的功率输出历史数据,从而建立风电场之间的出力相关性模型。如图5所示,即为风电场历史出力数据间的线性相关系数热度图。

图5 风电场出力线性相关系数Fig.5Linear correlation coefficients of wind power outputs
由图5中相关性热度图的整体情况可见,风电场2的出力与其余风电场出力间的线性相关系数较高,也即相关性更强。因此,选择建模根节点为风电场2的出力序列,基于动态C藤结构进行pair-Copula建模。如表2所示,即为基于动态C藤结构建模所得到的风电场出力模型最优Copula函数结果。

表2 风电场出力相关性模型的最优Copula函数Tab.2 Optimal Copula function of wind farm output correlation model
如图6所示,为时变t-Copula函数C36|297101458的参数变化过程。由图6可见,所建模型充分利用了动态Copula函数中相关参数的时变性,因此能更完备地描述C藤结构的动态特征。
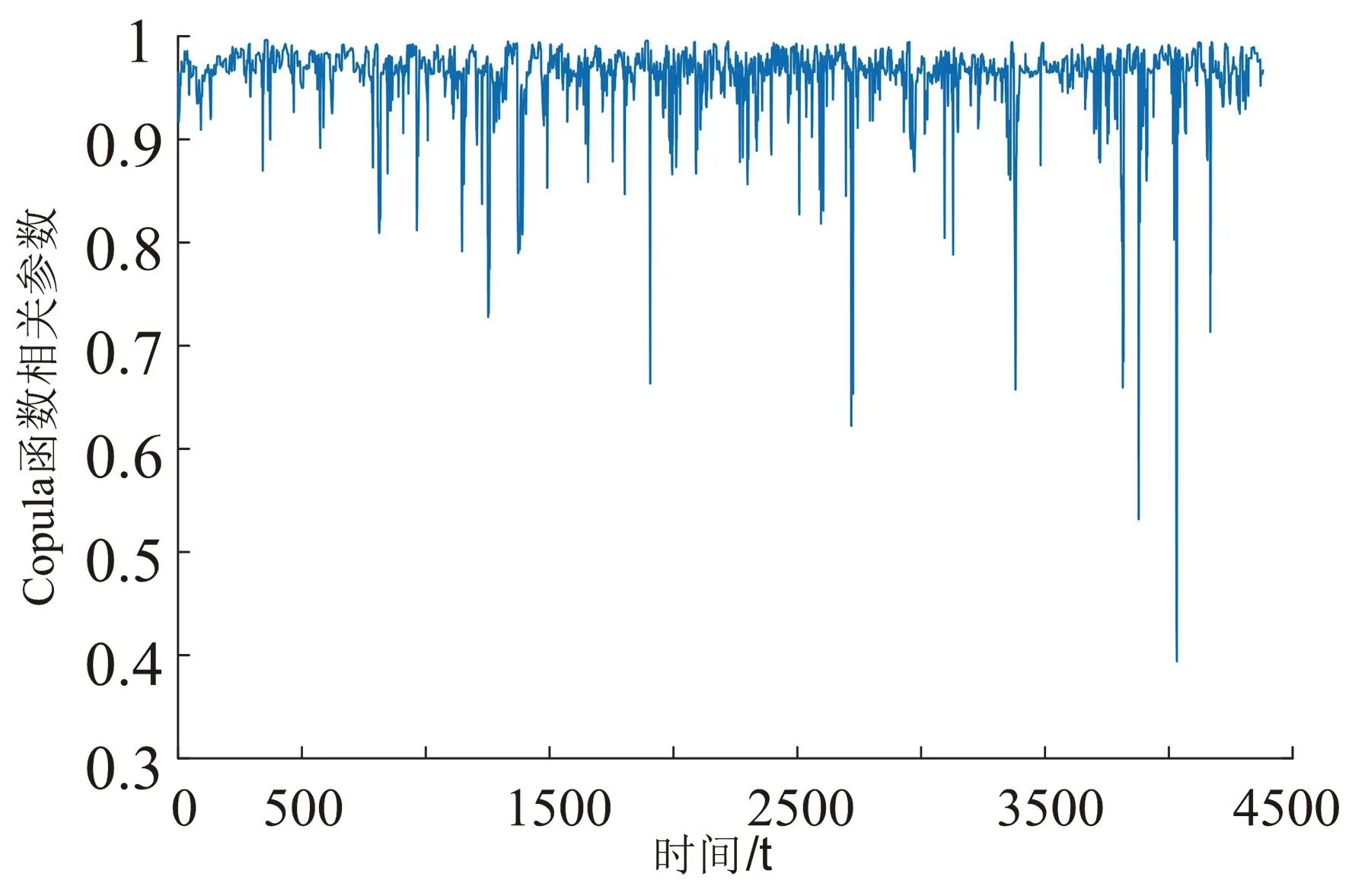
图6 时变t-Copula的参数变化图Fig.6 Parametervariation diagram of time varying t-Copula
为验证所建模型的有效性,计算10维风电场出力的静态pair-Copula以及动态pair-Copula模型的欧氏距离和AIC[29-31]值,如表3所示。同时,模型的K(z)检验结果由图7展示。
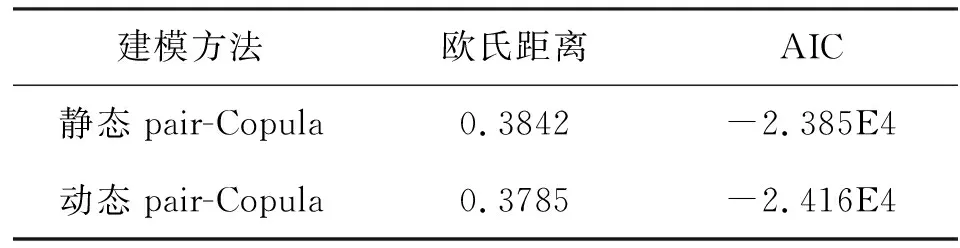
表3 不同pair-Copula模型的欧氏距离和AIC值Tab.3 Euclidean distance and AIC value of different pair-Copula models

图7 不同pair-Copula模型的K(z)检验Fig.6 K(z) test of different pair-Copula models
查看表3与图7的结果可见,本文所提模型对比采取静态Copula函数的pair-Copula模型,其 AIC值以及与经验Copula分布的欧氏距离更小。因此,基于动态C藤pair-Copula函数的本文模型拟合效果更佳,同时对高维新能源实际出力概率分布的表达也更为精准。另外,IEEE118节点系统不同区域的常规机组出力情况与全体风电机组各时段的出力曲线,如图8所示。
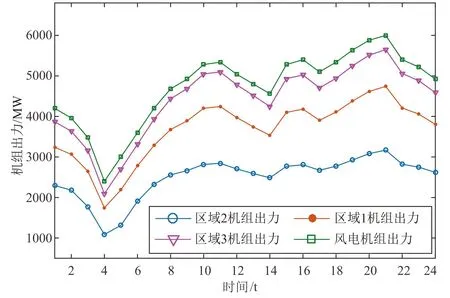
图8 IEEE118节点系统的机组出力曲线Fig.8 Unit power output curves of IEEE 118 node system
4.1.2 高维新能源的动态相关关系影响分析
基于是否考虑高维新能源的动态相关关系,分析其对于调度结果带来的影响。采用静态C藤 pair-Copula模型和不考虑风电场出力相关性的模型作为对比模型。然后,每个模型基于抽样技术生成10个随机误差场景。如表4所示,即为利用文中第2小节提出的MCO方法求解三种模型所得的结果。

表4 三种模型的结果对比Tab.4 Result comparison between three methods
由表4可知,对比不考虑高维新能源相关性以及只考虑静态C藤pair-Copula函数的情况,计及高维动态C藤pair-Copula函数的参数所具备的时变特性进行建模的系统总运行成本最低,经济调度结果最优。因此,考虑高维动态C藤pair-Copula函数进行建模,能够使得所建经济调度模型符合实际环境,从而将为含有高维新能源的电力系统动态经济调度模型提供更为精确的设计依据。
5 结论
本文基于动态Copula函数中参数所具备的时变特性,以及C藤pair-Copula函数的核心框架,构建了高维新能源出力的概率模型,该模型计及高维新能源出力之间的相关特性,对高维相依新能源结构的整体与局部特性进行了准确地刻画。其次,本文立足于多学科协同优化模型的思想,结合场景分析法求解含高维新能源接入电力系统的动态经济调度问题,不仅能够满足系统级优化模型在每次迭代中可行域存在的要求,而且可以反映出系统级问题最优解与误差场景级问题最优解间隐含的耦合关系。最后,基于IEEE118节点系统仿真验证结果表明:动态C藤pair-Copula模型能够完备地描述出高维相依新能源的实际结构特征,同时文中应用的基于场景分析的电网动态经济调度多学科协同优化算法具备降维求解能力强的优势。

