改进的小波阈值去噪法在省级电网低频振荡分析中的应用

刘默斯，孙志媛，李明珀，窦骞

(广西电网有限责任公司电力科学研究院，广西南宁 530023

电力系统低频振荡是指系统受到扰动后，系统中并列运行的同步发电机转子间发生相对摇摆导致系统中出现功率、电压等电量振荡的现象。低频振荡一旦发生，将持续较长一段时间才消失，严重威胁电网的安全稳定运行，可能造成大规模停电[1]。研究电力系统低频振荡的目的，就是要分析系统是否存在着弱阻尼振荡模式，并在系统中有弱阻尼震荡模式时，采取措施增强这些模式阻尼，以减少发生振荡可能，或者在产生振荡时，使其能尽快地平息振荡。

用于低频振荡模态辨识的信号处理方法有：傅里叶变换法、卡尔曼滤波法[2]、Prony法[3]以及HHT法[4]等。傅里叶变换对所处理的信号要求较高，当信号不满足绝对可积的条件时，傅里叶变换将无能为力，同时，傅里叶变换的时频窗口是固定的，这样不利于对信号不同频率成分进行分析，无法反映低频振荡模态的阻尼特性。卡尔曼滤波法存在反映不出低频振荡阻尼衰减特性的缺点，极大地限制在低频振荡分析领域的发展。HHT方法是一种自适应的时频分析方法，可根据信号本身的局部时变特性进行自适应分解，不仅可以得到很高的时频分辨率，还具有很好的时频聚集性。然而，HHT方法缺乏坚实的理论基础，其中EMD分解过程中存在诸多不确定因素，严重影响了该方法在低频振荡模态辨识中的可靠性。

Prony算法作为一种信号处理方法，用指数函数的线性组合来拟合等间隔采样数据，并能拟合出该数据的振荡幅值、频率、衰减因子和相位，辨识结果具有很高的准确性。但Prony算法的精度受信号噪声影响很大[5]，为此，研究者们开展了大量的研究工作以期找到一种具有良好的抗噪效果的方法。本文提出了基于改进阈值和阈值函数的小波去噪方法。最后经过仿真实验证明本文提出的改进小波阈值算法的优越性。

1 Prony算法简介

法国数学家Prony提出，可以用指数函数的一个线性组合来描述等间距采样数据的数学模型，形成能估算给定信号频率、衰减、幅值和初相的算法。

Prony算法是提取平稳振荡模式的常用算法。利用时域计算法对给定的运行方式和敏感故障形态进行时域稳定计算，得到发电机相对功角曲线或联络线功率变化曲线等，对所得曲线进行Prony分析可以得出曲线的各构成频率及其相应阻尼比等较丰富的信息，从而计算人员可以方便地知道某些需要重点关注的振荡模式的阻尼比是否满足动态稳定性运行标准。

Prony算法针对等间距采样点，假设模型是由一组p个具有任意幅值、相位、频率与衰减因子的指数函数的线性组合，其离散时间的函数形式为[6]：

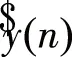
(1)

(n=0,1,…,N-1)

式中，Ai为幅值；θi为相位；αi为衰减因子；fi为振荡频率；Δt为采样间隔。N为采样个数。

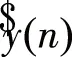
(2)

(3)

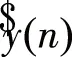
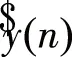
(4)

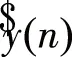
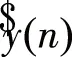
(5)

将(5)式代入(4)中可得：

(6)

做如下定义：

(7)

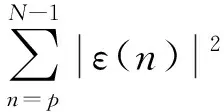
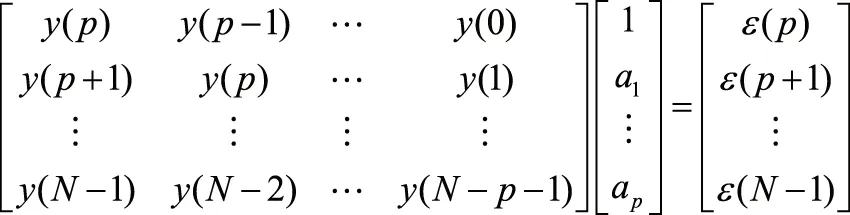
(8)

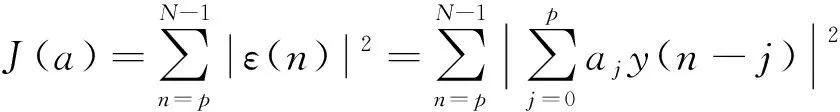
(9)

扩展Prony方法的主要步骤可以叙述如下：

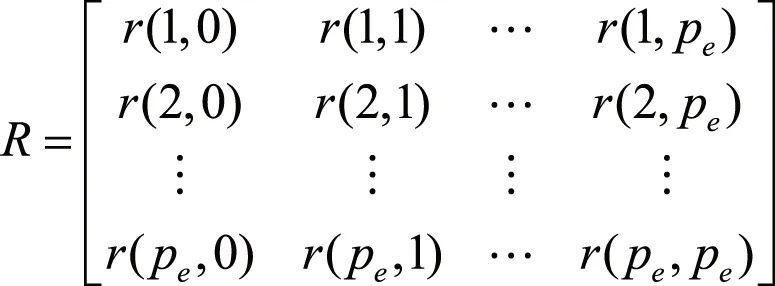
(10)

用奇异值分解的方法确定矩阵R的有效秩P以及系数a1,…,ap的总体最小二乘估计。

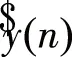
③将指数模型式(1)简化为未知参数bi的线性方程，用矩阵形式表示为：

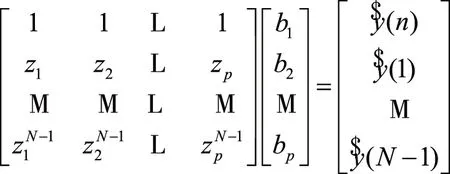
(11)

利用上式计算参数b1,…,bp。

④当系数b1,…,bp和z1,…,zp求出后，便可用下式计算幅值Ai、相位θi、频率fi和衰减因子αi：

(12)

在对输入信号进行预处理时，可以更有效地降低噪声信号的影响，从而提高Prony算法辨识结果的准确性。文献[7]将平滑滤波算法与Prony算法相结合，并采用插值算法以提高采样率。该算法在一定程度上提高了Prony算法的抗干扰能力和精度，但该算法灵敏度低，对偶然出现的脉冲性干扰的抑制作用较差。文献[8]采用小波阈值去噪，可以抑制噪声，但是文中采用的阈值是固定阈值，去噪的效果有待进一步提高。文献[9]提出了一种用于Prony算法的数字滤波器设计方案及幅相补偿方法：首先仿照周期信号滤波要求设计了模拟滤波器，针对模拟滤波器造成的Prony算法辨识的偏移，提出幅值及相位补偿方法，然后基于脉冲响应不变法将模拟滤波器离散化为数字滤波器，以此增强Prony算法的抗噪性。文献[10]提出了一种利用SDM方法确定Prony阶数的新思路，该方法受外界噪声影响小，能在短时间内准确辨识模态信息，适应性较强，但无法将高频干扰项和趋势项进行准确去除。文献[11]提出了一种在线去噪算法，用于检测采集数据中不可避免的测量噪声。所提出的去噪过程基于离散小波变换(DWT)，在噪声局部化和算法停止准则方面没有阈值。文献[12]在小波去噪的基础上对阈值进行改进，使得阈值随着小波的分解层数而改变，从而对输入信号取得了较好的滤波效果，但该文中的阈值函数采用的是硬阈值函数，仍有待改进以提高滤波效果。文献[13]提出了一种基于非凸稀疏正则化去噪和自适应稀疏分解的新方法，能够有效地从原始振动信号中提取出微弱的故障频率及其谐波。文献[14]通过小波变换方法进行同调机组分群，该方法可以有效地提取功角信号的特征信息，但是需要将测量数据分解为时空模式，以特殊的主振荡模式检测同调机群，对输入信号进行预处理时会带来计算负担。文献[15]提出一种基于Prony分析特征提取的同调机组分群方法，利用集成经验模式分解(Ensemble Empirical Mode Decomposition, EEMD)方法对含噪声的信号降噪。为消除原始信号中存在噪声或间断时，EMD存在的模态混叠现象，采用EEMD方法对量测功角数据进行降噪处理，通过本征模态分量和量测信号的相关系数来选取能真实反映原始信号特征的本征模态分量进行重构达到降噪效果。文献[16]通过采用互补集合经验模态分解(CEEMD)和小波包变换(WPT)相结合的去噪方法改善信号，对信号进行CEEMD分解得到固有模态函数(IMF)，并对得到的IMF 分量计算其排列熵(PE)值，根据排列熵值提取出含噪声较大的分量进行小波包去噪，然后将去噪重构后的IMF分量与剩余IMF分量重构信号进而提高Prony参数辨识的精度。文献[17]针对非平稳性、突变性和短时持续性的信号，提出一种基于提升小波和改进BP神经网络的扰动定位与识别方法。对扰动信号进行提升小波分解，并利用自适应学习率和增加动量项相结合的方法对BP神经网络改进并进行扰动识别训练。文献[18]提出了基于变分模态分解的电力系统泛频带振荡辨识方法，通过带通滤波器实现不同频段信号的分离，再利用有高噪声鲁棒性的变分模态分解(Variational Mode Decomposition, VMD)方法提取各个振荡模态信号，对信号中不同类别振荡模态进行有效区分与提取，精确识别每个模态的信息，针对已发生剧烈振荡的信号或是含有潜在振荡的类噪声信号进行模态辨识，但是该方法目前尚不能做到在线识别。

2 基于小波变换的信号处理

由上述分析和文献可知，在利用Prony算法时，需要对来自电力系统的实际信号进行去噪预处理，这样才能使得最后的结果更加准确。目前常用的适用于Prony分析法的去噪算法包括平滑滤波算法、模糊滤波法、小波阈值去噪法等方法，其中小波阈值去噪法因为灵敏度高、抗干扰力强和去噪效果好而应用广泛，但是常用的小波阈值去噪也存在自适应能力差、重构信号可能失真等问题。

针对以上问题，本文对传统的小波阈值去噪算法进行了改进，引入了新的阈值选取和阈值函数，实现了适用于Prony分析的小波阈值去噪算法，能够对待处理的信号进行去噪，提高Prony算法的准确性，有利于对电力系统低频振荡进行更准确的辨识，最大程度的降低噪声的影响。

小波信号是一类衰减较快的波动信号，其能量有限，且相对集中在局部区域。由小波函数ψ(t)经过展缩和平移构成小波函数族ψj,k(t)。由尺度函数φ(t)经过展缩和平移构成小波函数族φj,k(t)。利用小波函数族和尺度函数族，信号的小波展开式可表示为[19-20]：

(13)

展开系数cj0,k反映了信号y(t)中的低频分量的分布情况，而一系列展开系数dj,k反映了信号y(t)中的高频分量的分布情况，这些展开系数就是信号的离散小波变换。

信号的小波变换是对信号进行时频分析的有效方法，其对非平稳信号的线性时频分析在时频平面不同位置具有不同的分辨率，即小波变换是一种多分辨分析方法。

2.1 小波阈值去噪

含有噪声的信号y(t)的数学模型一般为：

y(t)=x(t)+ε(t)

(14)

式中，x(t)为有用信号，ε(t)为噪声信号。

对信号y(t)进行去噪处理的目的就是抑制其噪声信号分量ε(t)，从而恢复信号x(t)。

在频域对信号进行滤波时，是根据有用信号和噪声信号在频域所处的频谱分布的位置的不同从而对两者进行分离。一般认为，电力系统主要存在白噪声，而白噪声在较宽的频率范围内，各等带宽的频带所含的噪声能量相等，信号的谱和噪声的谱在频域重叠，基于频域的滤波是没有效的。

在信号的小波变换中，许多实际信号的展开系数大多集中在较少的系数上，为数据处理创造了有利条件。在基于小波变换的信号处理中，可以根据有用信号和无用信号的展开系数的幅值来分离信号的不同分量，有用分量对应的少数展开系数的幅值必然较大，而无用分量对应的多数展开系数的幅值必然较小。

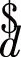
2.2 阈值的选取

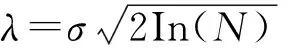
(15)

式中，σ为噪声强度，N为信号长度，σ=(median|dj,k|)/0.6745，median|dj,k|表示尺度j上的小波系数的中值。

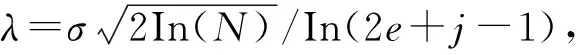
(16)

式中：Lj表示j尺度下，小波系数的长度。

取新的阈值为：

(17)

若第j层的小波系数中有用分量较多，则Wj的值会较大，λj的值就会相对较小；若第j层的小波系数中噪声分量较多，则Wj的值会较小，λj的值就会相对较大，这样阈值的选取便更符合实际中扰动信号的噪声分布[22]。新的阈值既考虑到了一般情况下随着尺度j的增加，小波系数的幅值是逐渐减少的，又兼顾了不同类型信号中噪声在各层的实际分布情况，弥补了文献[12]中阈值的不足。

2.3 阈值函数的选取

传统的阈值函数有硬阈值和软阈值函数两种。软阈值处理是将低于阈值的系数置为零，而高于阈值的系数也相应减少。硬阈值处理是只将低于阈值的系数都置为零。设λ为阈值，两种阈值函数的定义分别如下：

硬阈值函数：

(18)

软阈值函数：

(19)

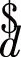
为了弥补传统阈值函数的不足，本文提出了一种改进算法：

(20)

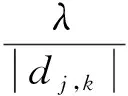
3 构造信号仿真实验

本文定义的信噪比为：

(21)

特别注意英文字母表示，要求如下：

(22)

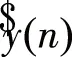
为了证明本文的改进去噪方法在小波阈值去噪方法中的优越性，构造信号：

y(t)=3e-0.25cos(2π×1.2t+180°)

+8.5e-0.15tcos(2π×0.6t+60°)

(23)

信号的采样频率为100Hz，采样点数为1000点。

对信号叠加10dB的白噪声扰动，然后在Matlab中分别采用软阈值法、硬阈值法、文献[12]所述基于小波去噪与扩展Prony算法相结合的高精度低频振荡模态辨识方法，以下简称改进阈值去噪方法以及本文的改进方法进行仿真实验。仿真中采用的小波基是sym6小波，分解层数为5层。仿真实验的结果如下图1及表1-2所示。

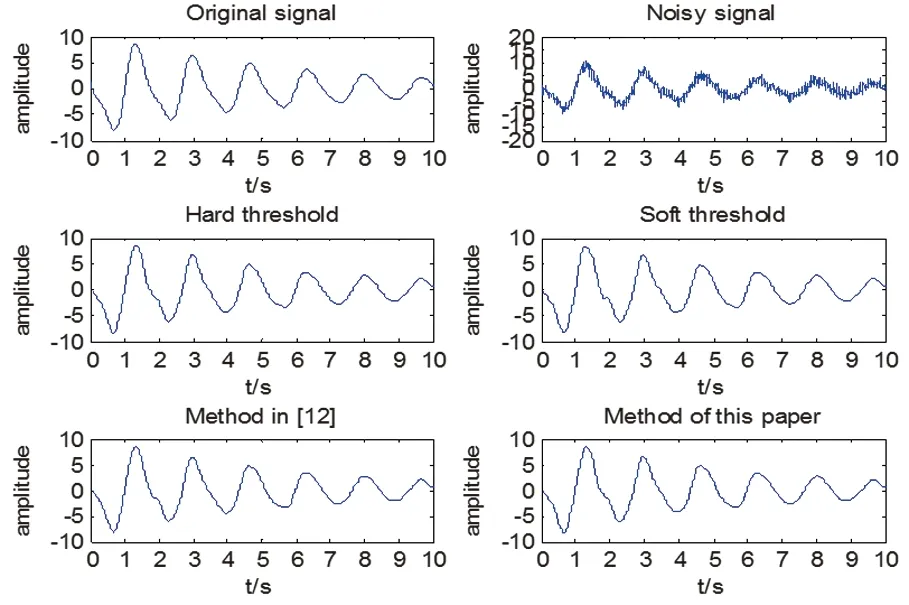
图1 四种方法去噪效果的比较图Fig.1 Comparison of denoising effects of four methods

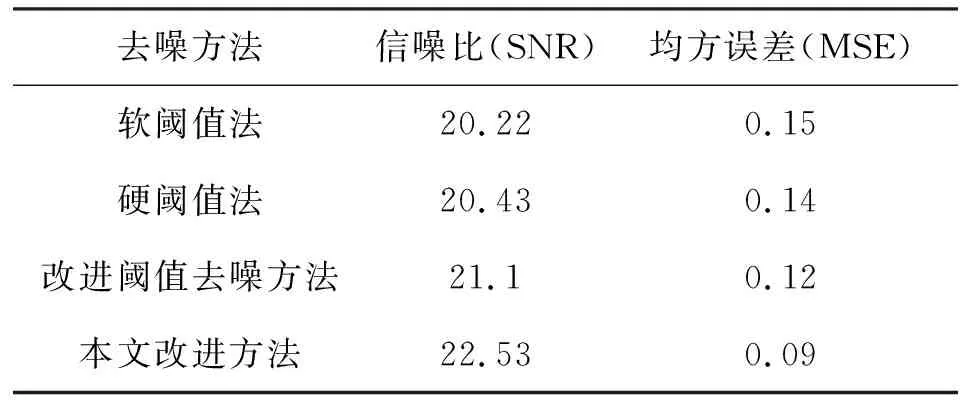
表1 四种方法的去噪效果比较Tab.1 Comparison of denoising effect of four methods

表1的结果可以看出，本文提出的改进方法的去噪效果在信噪比和均方误差意义上都优于其他几种方法。

对使用改进阈值去噪方法和本文改进方法去噪后的信号使用扩展Prony算法进行辨识，辨识的结果如表2所示。

表2 两种方法的辨识结果Tab.2 Identification results of two methods

从表2的结果可以看出，对含有噪声的信号，利用本文改进方法去噪后再使用扩展Prony算法能更准确地提取振荡模式参数。

4 结论

Prony算法由于其良好的数学特性而在电力系统低频振荡分析中得到了广泛的应用，但其对输入信号要求较高，对噪声较为敏感[23-25]。本文在分析传统的软、硬阈值函数以及固定阈值的优缺点后，提出了基于改进的阈值和阈值函数的小波阈值去噪算法。利用改进的小波阈值去噪算法对采样信号进行预处理，有效克服了噪声对Prony算法的辨识精确度的影响，有效提高Prony算法的抗干扰能力。

通过Matlab仿真实验分别采用软阈值法、硬阈值法、改进阈值去噪方法以及本文的改进方法进行比较，本文提出的改进方法的去噪效果在信噪比和均方误差意义上都优于其他几种方法，对信号使用扩展Prony算法进行辨识。对使改进阈值去噪方法和本文改进方法去噪后的信号使用扩展Prony算法进行辨识的结果表明，对含有噪声的信号，利用本文改进方法去噪后再使用扩展Prony算法能更准确地提取振荡模式参数。仿真验证了利用本文提出的改进小波阈值去噪算法对信号进行预处理能有效提高扩展Prony算法的辨识精确度。