基于LSTM神经网络的短期电能负荷预测

陈振宇，杨 斌，阮文俊，沈 杰，吴丽莉

(1.国网江苏省电力有限公司，江苏 南京 211106；2．国网江苏省电力有限公司苏州供电公司，江苏 苏州 215004；3．国网江苏省电力有限公司泰州供电公司，江苏 泰州 225000)

近年来，电力预测技术已逐渐从传统预测方法过渡到人工智能预测技术。支持向量机、神经网络的广泛应用大大提高了电力预测的精度。文献[1-2]利用最小二乘支持向量机(LS-SVM)预测模型，研究了在气象、日期等外部因素数据影响下对短期用电需求的预测、评估，不同预测周期下的实验结果同其他传统方法相比具有更好的准确性和可解释能力。SVM 进行预测能够克服神经网络易陷入局部最优解、运算时间长等常见问题，采用灰狼优化算法优化 SVR 参数后，对预测精度有一定的改善[3]。文献[4]是一种改进型果蝇优化算法，以风速子序列重构参数和最小二乘支持向量机(LS-SVM) 参数作为优化目标建立风速预测模型，相比LS-SVM 预测方法具有更高的预测精度。文献[5]建立了基于提升小波和改进PSO-Elman神经网络的短期负荷预测模型可平滑负荷序列的随机性和不确定性，具有较高的预测精度。文献[6]采用Stacking集成学习架构，建立了多模型融合的负荷预测模型，在数据测试中取得了优于单个模型的预测精度。同样处理电力负荷随机性较强导致预测精度不高的问题，通过构建集合经验模态分解以及门控循环单元神经网络和多元线性回归组合而成的 EEMD-GRU-MLR(EGM)预测方法，有效提高了电力负荷短期预测精度[7]。无论是发电企业、用电企业还是电力输送网络企业，对于详细的电力市场分析、精确的用户用电量预测和负荷特性分析的需求在不断地增长[8-10]。

本文首先分析了短期负荷预测的关键影响因素，以自回归方法为例介绍了传统负荷预测模型框架。接下来以BP神经网络和递归神经网络为例，阐述了神经网络模型原理以及与负荷预测任务的契合点。最后基于卢布尔雅那城市全年的真实负荷数据和气象数据，提出了基于电能负荷历史数据的递归神经网络预测方法，开展了基于长短期记忆单元的短期负荷建模预测研究。

1 相关工作

1.1 电能负荷的关键影响因素

智能电网的负荷预测、电网安全、谐波监测及安全预警等方面的需求特性决定了负荷预测的重要地位[11],电力负荷消耗同社会发展和自然因素等多方面因素密切相关。其中社会因素主要包括人口、经济、社会结构等方面，比如经济发达地区的能耗显著高于经济欠发达地区，人口密集区域能耗显著高于人口稀疏区域。但对于短时负荷来说，这些宏观因素可以视作常数，作用可忽略不计。相比之下，天气等短时变化十分剧烈的因素对于电能负荷的影响至关重要，也是负荷预测模型中考虑最多的因素。文献[12]为了准确实现天象与地表辐照度的实时映射关系，提出了一种基于深度学习的混合映射模型，用于太阳能光伏发电预测。

通常天气因素包含温度、降水、湿度、风速以及气象(如雾、霾等)[13]。其中温度是最重要的天气因素，因为人类活动和行为很大程度上受温度的影响，负荷和温度之间存在着很强的相关性。目前几乎所有新提出的短期负荷预测方法都以某种形式的温度作为预测的基础。降水对户外活动和一些工业过程影响较大，它的增加使得户外活动的负荷降低，室内活动的负荷升高。风速和风向组成了一个风向量，常被用来调整预测模型。当风力强过某一阈值时，负荷会降低；当风力低于某一阈值时，负荷会升高。云量对于以商业建筑用途的短期负荷预测非常重要，有很强的地域性，因为对照明的影响，从而对负荷也产生一定影响。湿度主要是运用在短期负载预测中，加上其他天气因素如温度等，可描述在一些气候条件下的负荷增加行为。

除此之外，电能负荷作为时序数据，另一个重要特性为周期性。对于每天的能耗数据，波峰与波谷总是根据用能对象出现在基本一致的时段内，并且负荷变化曲线基本一致。将时间尺度拉长，工作日的工业能耗明显高于休息日，而居民能耗则呈现相反的趋势。这一周期性本质上是由人类的作息制度导致的，反应在数据上，呈现出与时间的强相关性。

1.2 基于时间序列的传统负荷预测模型框架

时间序列分析是基于一串等间隔、连续时间的同类数据，采用之前时刻的数据，对未来时刻进行预测。目前电力系统通常配备有智能电表，可定时记录用能对象的用能数据，因此电能负荷预测显然很好地契合这一要求[14-17]。最典型的时间序列分析方法为自回归滑动平均模型(Auto Regressive Moving Average, ARMA)[18]。

(1)自回归模型AR

自回归即强调数据本身存在密切的耦合关系，采用历史值来对当前值进行描述，可以根据先验知识来确定历史跨度。一般的p自回归模型为：

(1)

其中ut为独立同分布的随机噪声，通常采用高斯白噪声。

(2)滑动平均模型MA

在自回归模型中，假如ut不是一个白噪声，通常认为它是一个q阶滑动平均，即：

(2)

其中εt表示白噪声序列。特别的，当xt=ut时，则

(3)

(3)自回归滑动平均模型(ARMA)

将AR模型与MA模型线性叠加起来，即构成了ARMA模型。

(4)

ARMA模型理论上十分适合时间序列数据的处理，但在实际应用中建模过程十分复杂，需要诸多专业的先验知识参与，并且对于偶然因素并不能做出可靠的预测。

2 递归神经网络与长短期记忆单元

随着人工智能技术的发展，对负荷预测提供了新的解决方案。文献[19]证实了深度 LSTM 具有对输入负荷数据特征学习以及长短期相关性挖掘的能力, 对区域级负荷可以取得很好的超短期预测效果。以神经网络为代表的建模方法，能够对数据内在的非线性关系和耦合进行很好地建模[20-24]。并且以长短期记忆单元为代表的递归神经网络能够充分挖掘数据之间的时序性关系，十分适用于负荷数据的建模预测。

2.1 BP神经网络

神经元是神经网络的基本单元，其基本结构如图1所示。

图1 神经元的基本结构Fig.1 Basic structure of neurons

其中pi,i=1,2,…,r为该神经元的i个输入值，wi,i=1,2,…,r为第i个输入对应的权值。f(·)是激活函数，b为偏置项，a为神经元的输出，输出的表达式为：

(5)

传统的BP神经网络由三个部分组成，输入层、隐层和输出层，如图2所示。BP神经网络算法的核心主要分为两个部分。一是输入信号的前向传递。数据由输入层输入，传递到隐层并进行计算，再通过输出层输出。二是误差的反向传播，在该阶段中，根据输出结果与真实值的误差，从输出层逐层反向传播，并逐层修改网络内的权值和偏置项，从而使得网络的输出能够接近真实值。

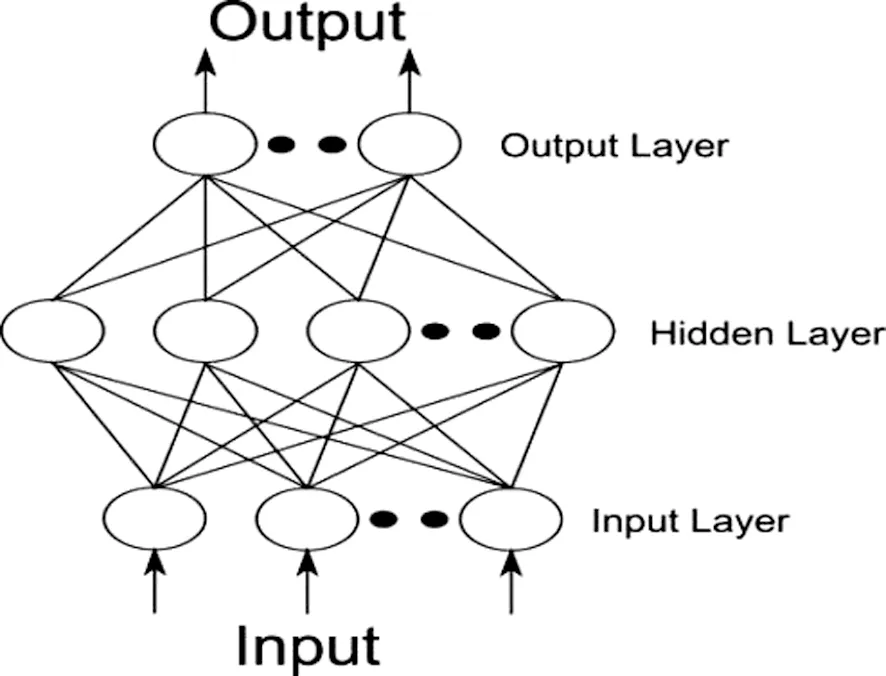
图2 BP神经网络的基本结构Fig.2 Basic structure of neural networks

2.2 递归神经网络

递归神经网络(RNN)的结构如图3所示，与BP神经网络结构不同的是RNN考虑了时序因素，存在着隐层到隐层自身的链接，即隐层的输出不仅传递到输出层，也将传递到下一时间步的隐藏层。这使得RNN的结构能够在一定程度上记忆历史信息，并利用历史信息计算当前神经元的输出，从而赋予了递归神经网络对时序数据进行建模的能力。

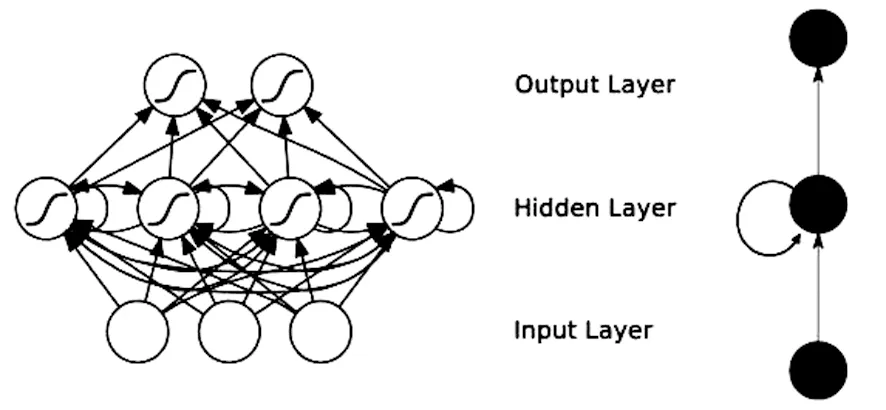
图3 RNN的基本结构Fig.3 Basic structure of RNN

RNN模型通过时序概念的引入，相比于传统神经网络存在非常大的优势，可在网络内部保存之前时刻学到的信息，在对每一时刻的数据进行处理时，都能利用之前时刻的信息，信息传递具有持续性，从而使得RNN能够很好地处理时间序列等周期性数据建模的问题。但是，RNN也存在一些明显的缺点。对于标准的RNN网络来说，当只使用与当前时刻相差不远的信息时，RNN的表现较好。但如果使用与当前时刻相差较长的信息时，RNN往往不能充分利用这些信息，这就是RNN的梯度消失问题。虽然在理论上RNN能够处理时间跨度很长的信息，但因为梯度消失的问题，在实践中RNN只能处理十分有限时间内的信息。

2.3 长短期记忆单元

为了解决RNN的无法处理长间隔强相关序列数据的缺点，长短期记忆(LSTM)模型可以做到这一点。最初的LSTM单元采用一个递归连接的记忆单元和输入门、输出门两个控制门限构成。记忆单元内存储神经元当前的隐态；输入门本质上是一个普通神经元，用来表示当前输入对隐态的影响；输出门表示隐态对LSTM单元输出的作用程度。直观地说，它们可以被看作是通过LSTM连接的数值流的监管者，因此被叫作“门”。在初始LSTM单元的基础上，将递归连接的记忆单元增加了一个遗忘门，提高了区分不同间隔的数据对记忆隐态影响的能力，提高了神经元性能[25-27]，因此被称作标准LSTM单元。LSTM基本结构如图4所示。

图4 LSTM的基本结构Fig.4 Basic structure of LSTM

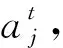
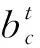
网络前向传播过程如下。

输入门：

(6)

(7)

遗忘门：

(8)

(9)

记忆单元：

(10)

(11)

输出门：

(12)

(13)

单元输出：

(14)

网络反向传播过程如下。

定义：

(15)

(16)

单元输出：

(17)

输出门：

(18)

状态：

(19)

记忆单元：

(20)

遗忘门：

(21)

输入门：

(22)

LSTM的提出，解决了传统RNN网络存在的梯度消失的问题，由于在误差的传播过程中，可以在有些神经元中通过“门”的结构完好无损地通过下一层而不发生衰减。从而使LSTM网络可以记忆长时间的信息，弥补了RNN的缺点。基于长时记忆的优点，LSTM网络如今在机器翻译、语音识别等领域展现了强大的建模能力。

3 基于LSTM网络的电能负荷预测实验

3.1 实验设置

本实验基于TensorFlow平台，TensorFlow是由谷歌2015年发布的第二代机器学习系统，被广泛地应用在各种机器学习任务中。实验所采用的数据集是来自斯洛文尼亚卢布尔雅那市2011年全年的电力负荷数据。在负荷之外也包含着其他的信息，包括温度、湿度、压力、风向和风速。因此除去时间戳外，每条数据的维度为7。原始数据的粒度为几分钟，各个数据点的测量间隔也稍有不同，故采用了取平均值的方式将其整合为粒度为一小时的数据。截取的部分实验数据如图5所示。

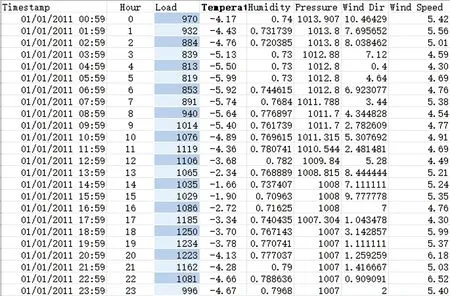
图5 实验数据样表Fig.5 Experimental data sample

根据前文所讨论过的电力负荷预测的影响因素与分类，该数据集只包含了时间数据和天气数据，缺少经济因素与社会因素数据。时间长度上也较短，只有一年，因此该数据集较为适合开展短期负荷预测，难以进行中长期的负荷预测。故本文将进行预测时长分别为一小时和一周的短期负荷预测实验。实验数据按照4∶1的比例，将前80%的数据(7008条)用作训练集，后20%的数据(1752条)用作测试集。另外，由于不同的数据在量纲上的不同，在天气数据输入网络前需要将其归一化到(0，1)的范围内。

为了判断模型的效果好坏，需要有一种方法来量化模型的预测性能。本文使用平均绝对百分误差(MAPE)和均方根误差(RMSE)来衡量模型的预测结果。

MAPE的计算公式如下

(23)

RMSE的计算公式如下

(24)

其中yi代表i时刻的实际值predi代表i时刻模型的预测值，n为样本总量。由这两个公式易知，MAPE、RMSE越低，代表着预测模型的精度就越高。

3.2 实验内容与结果分析

3.2.1 基于前日数据的当前时刻负荷预测

首先为了检验LSTM网络对于超短期负荷预测性能，在一小时尺度下，设计使用前一天的所有信息来预测当前时刻电力负荷值，故输入层含有7×24个神经元，输出层为1个神经元，中间的隐层设计为2层，第一层包含20个LSTM单元，第二层包含50个LSTM单元。损失函数使用平方误差，采用Adam算法对网络进行训练。Adam算法是一种随机梯度下降的扩展方法，它能基于训练数据迭代地更新神经网络权重。随机梯度下降保持单一的学习率来更新所有的权重，学习率在训练过程中并不会改变。而Adam通过计算梯度的一阶矩估计和二阶矩估计而为不同的参数设计独立的自适应性学习率，能够使得参数收敛到更优的结果并加快运算的速度，具有良好的适用性。初始学习率设为0.0005，Loss曲线结果如图6所示。输入测试数据进行预测并与实际值进行对比，得到的结果如图7所示。

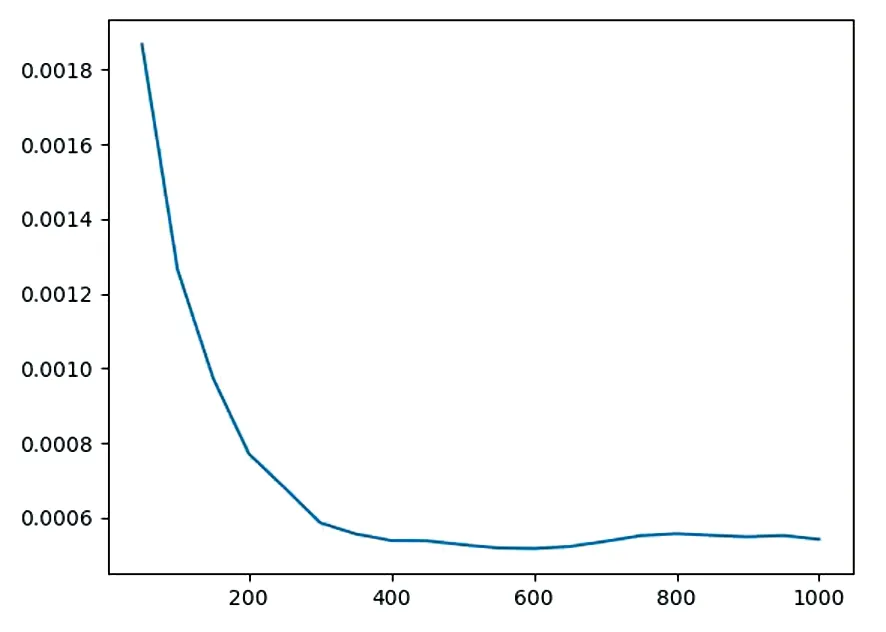
图6 Loss曲线Fig.6 Loss curve

图7 连续一周的预测效果Fig.7 One consecutive week of prediction

由图6迭代次数与损失函数的关系可以看出，当迭代次数达到1000次时，损失函数的值已基本不变，可以认为模型已经收敛。图7中，蓝色线是实际值的曲线，橙色线是预测值的曲线。从以上的实验结果图中可以看出，基于前一天历史信息的单步预测效果较好，预测值与实际值的变化趋势相同，绝对误差也较小。计算得到MAPE为2.09%，RMSE为47.30。

3.2.2 基于上周数据的一周负荷预测

接下来为了检验更大时间跨度下LSTM网络对于负荷预测的效果，依旧在一小时尺度下，设计使用一周的能耗和天气数据来预测下一周的电力负荷值，修改模型输入改为7×168，输出为1×168，其他结构保持不变。基于该模型的连续两周预测数据如图8所示，可以看出，相比于预测时长为一小时的结果，预测时长为一周时，预测结果开始变差。绝对误差较高，但预测值的变化趋势与实际值仍较为相符。说明网络对于预测较长时间后的负荷值的能力有限，但学习到了每周、每日的周期性变化规律。计算得到RMSE为140.71，MAPE为7.03%。

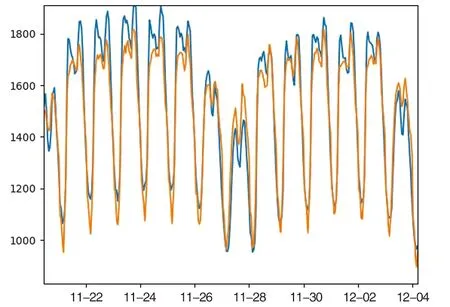
图8 连续两周预测效果Fig.8 Two consecutive weeks of prediction

3.2.3 基于上周数据和星期的一周负荷预测

对于电能负荷数据来说，一个基本的先验知识是能耗数据除了自身呈现周期性特征以外，这样的周期性与时间还存在着密切关系。在一周跨度下，对于城市整体而言，通常工作日用电量较高，而休息日会明显降低。因此考虑在原有序列数据条的基础上，加入one-hot编码的星期信息来显式地描述能耗模型的周期性特性。修改模型输入维度至(7+7)×168，其余部分保持不变。

截取与图8相同时间段的部分实验测试结果，如图9所示，可以看出引入日期这个周期性因素后，网络模型对于尖峰负荷的预测更为准确。计算得到RMSE为130.19，MAPE为5.99%，在加入了星期信息后，两项指标数值均有所降低，即预测精度稍有提高。验证了基本先验知识，日期信息，对存在着以一周为周期的时间序列建模的帮助。

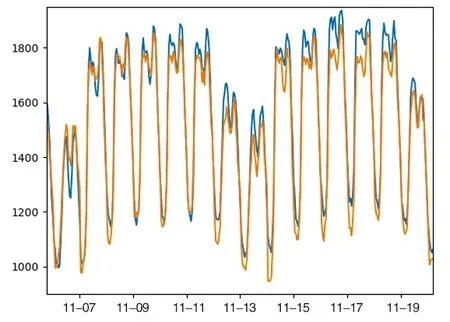
图9 基于历史数据和气象数据模型的连续两周预测效果Fig.9 Two consecutive weeks of prediction based on historical data and meteorological data mode

4 结论

本文分析了影响短期电能负荷的关键影响因素，回顾了以往对于负荷预测的研究、建模方法。以对时序数据的建模能力为主要切入点递进地分析了BP神经网络、RNN和LSTM网络。选择了能够记忆长短时信息的LSTM网络作为实验使用的预测模型。

根据数据集的特性，本文实验以短期负荷预测为主题，从预测时长为一小时和一周两个方向分别搭建了对应的LSTM网络。一小时的预测模型效果较好，一周的预测模型由于预测时长较长而效果相对较差，但通过增加星期信息的输入，使得预测效果有所改善。验证了基于历史数据和天气对于短期电力负荷预测的有效性和星期信息对以一周为周期的时间序列建模的明显帮助。