基于张量积压缩感知的高效安全的影像传输
王成宇 ,陈自刚 ,李书芳 ,王怡宁
(1.北京邮电大学信息与通信工程学院,先进信息网络北京实验室,网络体系构建与融合北京市重点实验室,北京 100876;2.重庆邮电大学信息与通信工程学院,重庆 400065;3.中国医学科学院北京协和医院放射科,疑难重症及罕见病国家重点实验室,北京 100730)
1 引言
随着网络带宽的增大,医学影像通过互联网进行传输的需求增大,同时面临保证数据传输的安全性以及完整性的挑战。压缩感知技术是一种兼具压缩与加密特性的技术,与云存储以及大数据计算平台已成为医院网络架构场景中的热点话题[1]。
解决医学图像的存储空间占用问题以及传输安全面对挑战。首先,图像的信息安全应该得到保障。为满足卫星图像传输安全,提出基于替换图像像素并通过密码学改变图像像素分布的方案[2]。通过共享秘密图像以及密钥保护的方案,能够达到隐藏彩色图像信息的效果[3]。基于SSH协议与密钥加密技术开发出医学图像传输的应用软件[4]。
图像的传输速度也是一个值得关注的话题。基于压缩感知技术提出一种端到端的图像压缩系统,融合了图像重建、量化以及熵编码等技术,加快医疗系统中的图像传输速度[5]。通过允许快速访问大量医学图像数据的框架,通过在线网页客户端进行图像展示实现数据的实时交互[6]。
海量的医学图像的存储占用巨大的空间,解决空间占用问题具有一定的挑战。提出区块链的医疗数据管理以及云上存储的模式[7],为解决海量医学图像的存储提供了新的思路。通过私有云对图像进行加密以及解密,公有云对图像进行存储的模式[8],不仅可以解决图像的存储问题还可以为图像信息安全提供保障。基于云存储提出一种可扩展传输速度更快的系统,可以实现图像的存储以及检索等操作[9]。
然而,大多数上述的工作仅致力于解决当前面临的三个问题中的一个或者两个。我们提出基于压缩感知技术、混沌系统以及云上存储的方式实现医学影像的传输系统。此系统可以加快云端图像的上传以及下载速度,同时由混沌系统实现的双重加密可以保障云端数据的安全性。基于新型的张量积压缩感知模型,使用张量积的方式生成高维矩阵,同时采用迭代加权最小二乘(Itera‐tive weighted least squares,IRLS)算法对图像进行还原重建能够保证对压缩图像的高精度重建。为确保图像信息的安全性,使用双重Chen-chaotic 系统分别对压缩图像进行空间置乱以及像素值加密,具备密钥空间大、密钥高敏感度的特点,能够保障信息安全性。
2 相关工作
2.1 传统感知模型
传统压缩感知模型基于欠定性方程的一种特殊情况

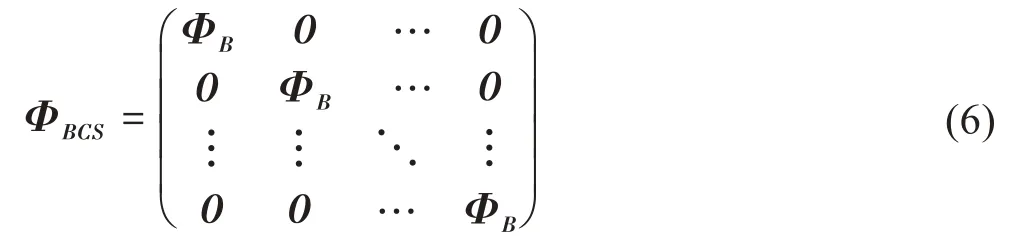
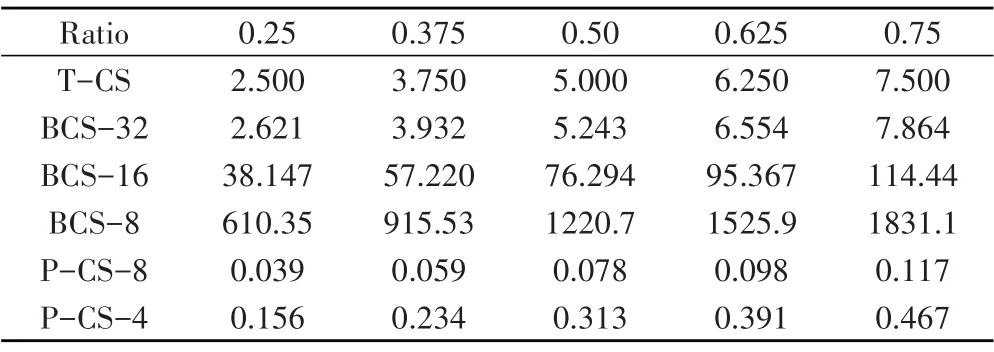
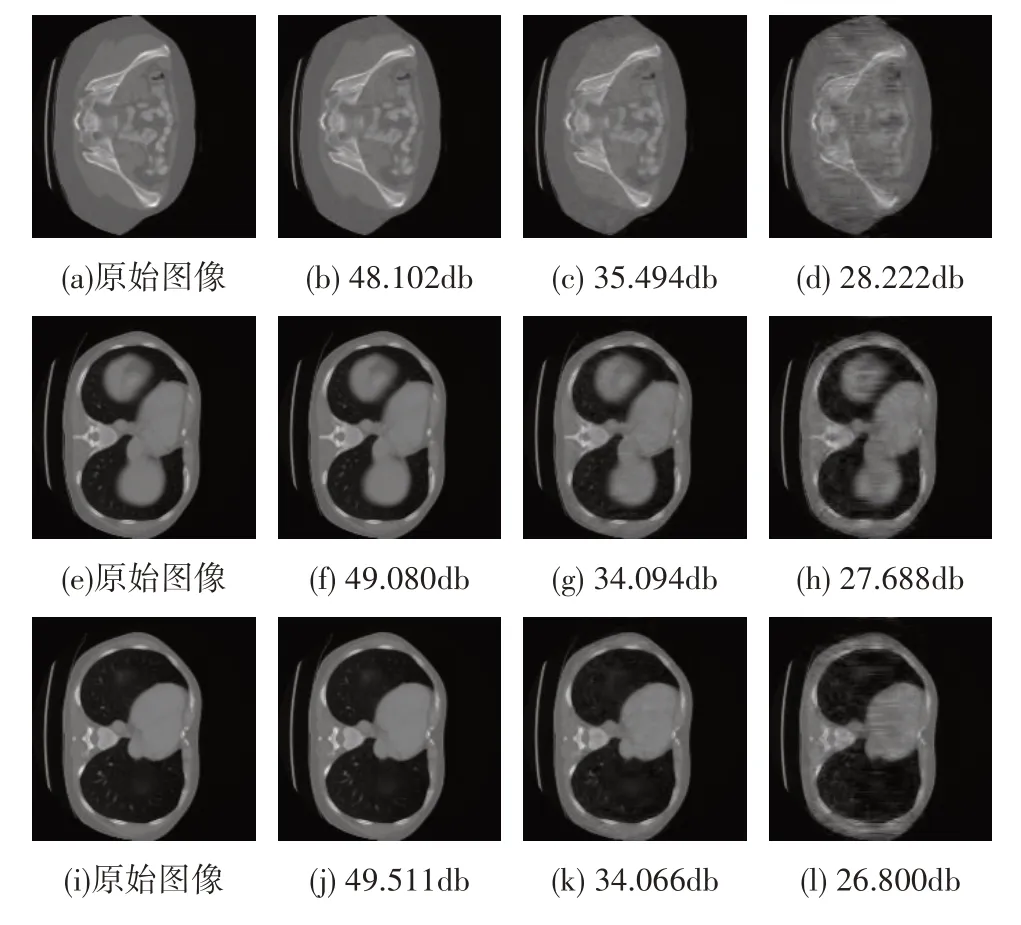
等式(1)表示原始信号x∈Rn经过非线性采样压缩为y∈Rm且m 其中Ψ为正交稀疏基,Ψ∈Rm×n,最常用的正交稀疏基为离散小波变换(Discrete Wavelet Transform,DWT)基与离散余弦变换(Discrete Cosine Transform,DCT)基。由等式(1)与(2)可以得到压缩感知模型的最终模型表达式 有限等距原则(Restricted Isometry Property,RIP)能够保证信号的重建能够保证唯一且准确[10]。Spark常数可以衡量测量矩阵内的列的线性相关性,保证信号的采样能够准确唯一的还原。Coherence常数衡量θ内向量的最大内积,反映两个列向量的相似性。基于以上三个性质,能够保证信号能够唯一且准确的还原重建。 分块压缩感知模型,基于将原始图像分成大小相同的子图像的思想达到降低计算复杂度的效果[11] 其中Xi表示子图像块,设原始图像大小为q×s,被分为N个子图像快,由于每一块子图像使用相同的测量矩阵进行采样,因此可以达到降低测量矩阵存储空间的效果。分块压缩感知模型框架为 对于原始图像测量矩阵可以表示为 分块压缩感知模型的提出能够在图像未完全呈现时就可以将图像进行压缩,适用于卫星图像以及遥感图像领域的应用。 提出的医学影像传输系统由三部分组成,包括负责图像压缩的压缩感知模块、图像加密模块以及图像解密重建模块。 传统的压缩感知模型[12,13]中,测量矩阵必须与图像矩阵的维度匹配才可以进行矩阵的乘法运算。张量积压缩感知模型中,设图像矩阵表示为X∈Rq×q,离散小波变换(a discrete wavelet transform,DWT)基是一个正交稀疏基表示为Ψ∈Rq×q,则图像矩阵的稀疏域转换过程表示为 其中,S∈Rq×q表示X的稀疏域。 提出的压缩感知技术的关键不同在于构造测量矩阵的方式。提出的压缩感知的框架可以表示为: 其中⊗表示Kronecker product。设有矩阵Φ ∈Rm×n,P∈Rt×t,m 于是,(Φ⊗P) ∈R(m×t)×(n×t)并且,我们称为压缩率,将q/n称为矩阵的放大系数。 在P 张量积压缩感知中,矩阵Φ是一个随机矩阵,例如Gaussian 矩阵、Bernoulli 矩阵、Chaotic 矩阵。而矩阵P 可以是一个单位矩阵也可以是一个随机矩阵。在本实验中矩阵Φ与矩阵P都使用Chaotic矩阵。 在加密模块中,矩阵Φ是由第一个Logistic-chaot‐ic系统生成,系统参数为(Φµ,Φx0,Φd),矩阵P由另一个Logistic-chaotic系统生成,系统参数为(Pµ,Px0,Pd)。Logistic-chaotic 系统中的控制参数µ∈( 3.569 946,4),初始值x0∈(0,1),采样距离d∈(15,+∞)。两个系统的系统参数是我们加密系统中的密钥的一部分。基于共享密钥的加密方式与压缩感知的方式结合可以提供具备安全性与鲁棒性的加密算法。 图像矩阵X∈Rq×q经过压缩采样后得到观测矩阵。将压缩后的图像矩阵进行量化处理,将矩阵Y 中的元素的数值值域转换至[ 0,2α-1 ],可以表示为 其中,α为正整数,Ymax为矩阵Y 中的最大元素的值,Ymin为矩阵中的最小值。 对于量化后的图像矩阵使用Chen-chaotic系统进行双重加密,系统中的参数为,i=1,2。其中为采样距离,其它参数为系统的初始值并且取值范围都为(0,1)。使用Ai∈表示Chenchaotic系统生成的混沌矩阵, 其中Si为得到的混沌序列,将第一个Chen-chaot‐ic系统产生的混沌序列使用C表示,对C1进行排序后的序列使用C1_SORT表示,空间置乱加密算法如下算法1所示: 算法1 第一步加密算法伪代码描述 将第二个Chen-chaotic 系统产生的序列使用C2表示,生成过程为 将混沌序列C2转化为维数为×q的矩阵,表示为C2m。第二次的加密方式为对图像矩阵进行像素值加密,描述为 其中,β∈(0,1),N2m∈。 描述中,将生成测量矩阵的过程也看作为加密的原因是压缩感知中的图像压缩过程本质上也是改变图像的像素值,而且基于这种方式可以很好的将压缩感知的加密特性进行量化评估。同时基于Chen-cha‐otic混沌系统的加密方式属于无损加密。 图像的解密过程就是加密过程的逆过程,根据得到的正确的密钥构造Chen-chaotic 序列C1与C2,接收到的图像矩阵设为N2m_r∈,则解密过程为 则N1d为第二次加密的解密结果。 第一步加密的解密过程实质上为将图像矩阵中的像素值的位置进行还原,即为空间置乱的逆过程,解密算法如算法2。 算法2 第一步加密的解密算法伪代码描述 加密图片完成解密之后,进行量化过程的逆过程观测矩阵即压缩后的图像矩阵使用Yr表示,描述为 最后,对观测矩阵进行还原重建得到相对精确的图像矩阵。还原算法为IRLS 算法,由于矩阵的还原算法为逐列进行还原,因此IRLS 对每一列的还原过程使用伪代码的形式进行描述,如算法3 算法3 IRLS算法伪代码描述 因为原始图像在进行压缩之前进行了稀疏域转换,因此观测矩阵的每一列符合x∈∑k的稀疏原则,因此图像能够被成功且精确的还原重建。 在本章节中,我们对提出的压缩感知模型以及加密算法进行实验检测。详细对比与其它压缩感知模型下在测量矩阵方面的优势,并且找到与提出的压缩感知模型相匹配的还原重建算法,最后检验加密算法的性能。 由于测量矩阵需要与图像的维数相匹配,当面临压缩感知的图像维数较大时,会造成测量矩阵的空间占用过大的问题。而我们提出的P 张量积压缩感知模型与传统的压缩感知模型以及分块压缩感知模型(Block Compressing Sensing,BCS)构造测量矩阵的方式不同。由于P 张量积压缩感知模型与半张量积压缩感知模型构造测量矩阵的方式相同,因此在测量矩阵生成时间以及空间占用方面的表现相同。 采用不同的压缩感知模型对尺寸为1000 × 1000的图像进行压缩,图像压缩率ratio。传统压缩感知模式下测量矩阵内的元素个数为1000 × 1000 ×ratio;分块压缩感知模型下,设将图像分为Nb块,则测量矩阵内的元素个数为×ratio;在P张量积压缩感知模型下,设测量矩阵的维度放大系数为NP,则测量矩阵内的元素个数为×ratio。在不同的压缩率下各个压缩感知模型构造测量矩阵时矩阵内的元素的个数如表1,表格中元素数值的量级为105。 表1 不同压缩感知模型下的测量矩阵所需元素个数 从表1可以看出分块压缩感知模型与P张量压缩感知模型都比传统的压缩感知模型需要更少的矩阵元素,同时由于在分块压缩感知模式下如果图像分块数量较大,造成每一块图像维数过小,使得图像还原重建效果不理想。因此,P 张量积压缩感知模型构造的测量矩阵能够在保证图像还原重建效果的前提下降低测量矩阵的空间占用。 P 张量积压缩感知模型下,不同压缩率下图像还原重建效果,如图1,其中第一行为原始高分辨率图像,从第二列至最后一列分别为0.75、0.50、0.25 的压缩率下的还原重建图像及其对应的峰值信噪比(Peak Signal to Noise Ratio,PSNR) 图1 P张量压缩感知对三张医学图像进行压缩的还原重建效果 由于Chaotic 测量矩阵是通过在混沌序列中进行等间距采样的方式构造的,同时采样间距d必须满足d≥15 的条件才能够保证矩阵内的元素相关性足够低,通常d的设置为1000,从而造成生成测量矩阵的过程中需要生成长度很大的混沌序列,造成Chaotic测量矩阵的生成速度较慢且占用空间较大,应用的广泛性受到限制。表2 中为对尺寸为512 × 512 的图片进行采样压缩,构造测量Chaotic 矩阵所需要的时间,随着矩阵的放大系数的增大所需时间大幅下降(单位:毫秒)。 表2 不同压缩感知模型下的测量矩阵所需元素个数 P 张量积压缩感知模型下,不仅能够降低生成测量矩阵的空间占用同时能够降低测量矩阵的生成时间。 在P 张量积压缩感知模型下,通过设置不同的矩阵放大系数分别为1、2、4、8、16,对尺寸为512×512 的图像进行采样压缩,以及还原重建,如图2 所示。不同的测量矩阵在P 张量积压缩感知模型下的表现,特别地,当q/n=1 时,为传统压缩感知模型下的测量矩阵表现,P 张量积压缩感知模型下能够保证测量矩阵的性能的前提下降低存储空间占用。 图2 P张量积压缩感知模型下测量矩阵性能对比 使用IRLS 算法以及正交匹配追踪(Orthogo‐nal Matching Pursuit,OMP)算法,测量矩阵为chaot‐ic 矩阵,进行10 次重复实验。可以看出在传统压缩感知模型下IRLS 算法与OMP 算法的表现几乎相同,但是在P 张量积压缩感知模型下,IRLS 算法的优势逐渐明显。同时随着矩阵的放大系数还原重建的稳定性降低,这是由于测量矩阵的维数降低,测量矩阵性能受到影响。IRLS 算法与P张量积压缩感知模型更为契合。如表4 中图像还原重建的PSNR 值。 表3 不同压缩感知模型下的测量矩阵所需元素个数 表4 图2中图像的数据结果(单位:dB) 加密算法由两部分组成,包括Chen-chaotic 系统和生成chaotic 测量矩阵的Logistic-chaotic 系统,=1,2,为加密系统密钥的组成。的密钥空间以及密钥敏感性相同,设密钥空间为S1,(Φµ,Φx0,Pµ,Px0)的 密钥空间为S2,Φd与Pd的取值空间为[ 15,S3],Pd的取值范围为[ 1,S4],经过混沌序列误差实验 得到加密算法的密钥空间为 其中S1为16,密钥敏感性为10-16,同理S2为15,取S3为1000,S4为100,故加密算法的密钥空间为10200。足够抵抗暴力破解的攻击,保证信息安全性。图3 为分别对每一个密钥进行敏感度实验,测试每一个密钥在错误为1 个敏感度时的解密效果。 从实验结果中可以看出加密算法能够抵抗暴力破解,同时具备密钥高敏感性、密钥空间大的特点。初次之外,我们还进行了关于图像的信息熵的实验,加密图像的信息熵可以达到7 左右,同时分析加密图像的像素相关性发现加密算法性表现良好,原始图像各个像素相关性为1 左右,加密后的图像的像素相关性为0 左右。同时由于加密系统中考虑到了图像像素值篡改的问题,将密钥的组成部分与图像的像素值相关联,达到了防止篡改的目的。 本文提出的基于P 张量积的压缩感知的医学影像传输系统,能够降低存储空间占用保护图像信息内容的安全,缩短测量矩阵生成时间加快压缩过程。实验结果表明,提出的压缩感知模型具备高效性以及稳定性。提出的加密算法在密钥空间上表现突出,密钥具备高灵敏度。

2.2 分块压缩感知模型


3 提出的医学影像传输系统
3.1 张量积压缩感知模型




3.2 加密算法



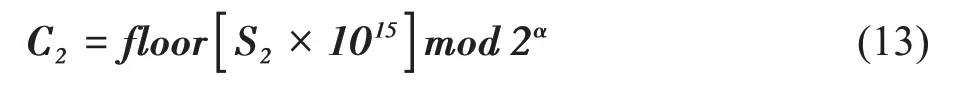

3.3 解密与图像的还原重建


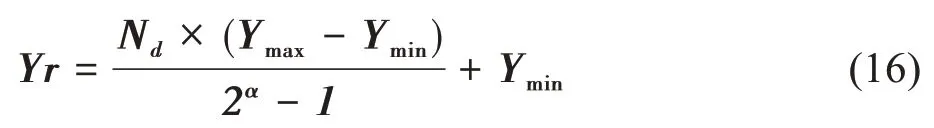


4 实验及结果分析
4.1 生成测量矩阵的效率以及空间占用对比

4.2 测量矩阵性能对比

4.3 重建算法对比


4.4 加密算法性能

5 结论与展望

