基于神经网络的后均衡方法在水下可见光通信中的应用

李国强,王超凡,李忠亚,邹鹏,胡昉辰,迟楠

（复旦大学通信科学与工程系，电磁波信息科学教育部重点实验室，上海 200433）

1 引言

随着社会的发展，人类进一步推进对海洋环境的探索，伴随着水下机器人的研究、水下传感网络的搭建以及水下大数据的应用，人们对于水下通信技术提出了更高的要求。相比于传统的水声通信和水下射频通信，水下可见光通信具有高速、低延迟、高保密性的优点，引起了广大研究者的关注［1］‐［3］。

然而，水下信道环境很复杂，湍流、漫射、散射等因素严重影响信号传输的质量，同时在可见光通信系统中，由器件带来的非线性失真也限制着系统的性能。传统的基于自适应滤波器的均衡方法，比如最小均方误差（Least Mean Square,LMS)、递归最小二乘（Recursive Least Square,RLS）和基于Volterra 级数的滤波器，有助于缓解一部分的线性与非线性失真，但是在系统非线性较强的情况下，其带来的性能提升有限。为了满足未来水下可见光通信往更大容量、更高速率发展的需求，需要找到更加先进的信号均衡方法。

近年来，神经网络被广泛应用到图像、医疗等领域，其根据训练样本和标签来拟合输入输出之间的复杂映射，并开始被应用到可见光通信的信号均衡中。在文献［4］中，深度神经网络（Deep Neural Network,DNN）被应用到基于无载波幅相（carrier‑less ampli‐tude and phase,CAP）调制的可见光通信系统中。实验证明，DNN 在非线性均衡方面要优于传统的自适应滤波器的方法。在文献［5］中，YihengZhao 等人提出了基于双支多层感知机（Dual‑Branch Multi‑Layer Perceptron,DBMLP）的后均衡方法，有效解决了DNN计算复杂度高的问题，并基于该方法实现了3.2Gbps水下可见光传输。上述两种方法均只考虑了信号的时域特征，而Hui Chen等人将信号的频域特征也加入到神经网络的训练中，提出了基于时频联合图像分析的神经网络（joint time‑frequency post‑equalizer based on deep neural network and image analysis,TFDNet)［6］，实验表明TFDNet能够有效补偿可见光通信中的非线性失真。神经网络在可见光通信中的应用受到越来越多人的关注。

本文介绍了基于神经网络的后均衡方法在水下可见光通信中的应用，从原理出发，通过实验对比分析了DNN、DBMLP 和TFDNet 三种网络在非线性均衡方面的性能，并且讨论了不同计算复杂度对三者的影响，为在实际应用中采用不同的均衡方法提供参考。

2 神经网络后均衡方法的基本原理

2.1 基于深度神经网络的后均衡方法

基于万能近似定理，深度神经网络（DNN）具有解决复杂非线性问题的能力，将其应用在可见光通信中，可以模拟系统存在的非线性失真，进而完成对信号的均衡作用。基于DNN 后均衡的原理框图如图1所示，其中包括输入层、隐藏层和输出层，在后均衡的过程中，首先将接收到的时域数据通过一个滑动窗口转化为一系列的并行数据，并输入到DNN 的输入层，此操作是为了考虑周围数据点对当前点的影响，滑动窗口的长度与DNN 输入层的节点数N 相同。随后，DNN 在训练的时候进行误差反向传播和权重更新，最后输出经过均衡的串行数据。在实验的过程中，所用的DNN 包括一个隐藏层，隐藏层节点的激活函数为线性整流函数（Rectified Linear Unit,ReLU)，其函数表达式可由公式（1）表示：

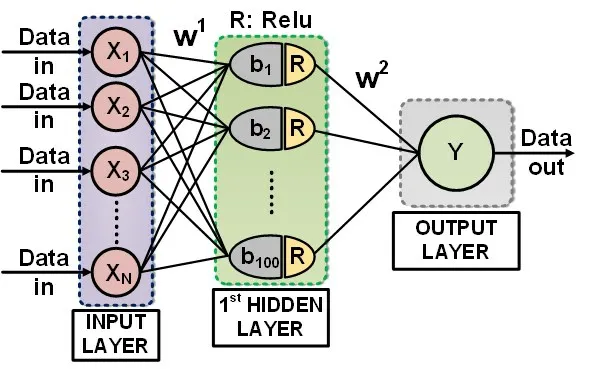
图1 深度神经网络后均衡原理图

2.2 基于双分支多层感知机的后均衡方法

基于DNN 的后均衡方法能够在强非线性的情况下取得比较好的均衡效果，但是其需要比较高的计算复杂度，不利于其应用在实际的通信系统中。基于双分支多层感知机（DBMLP）的后均衡方法有助于降低神经网络模型的空间复杂度，其原理框图如图2 所示。与DNN 类似，DBMLP 包括输入层、隐藏层和输出层，DBMLP的隐藏层由两个分支组成，一个是线性映射分支，完成输入信号与标签的线性映射，而另一个是非线性残余分支，用于均衡线性映射分支输出信号的非线性残余噪声。线性映射分支的输出可由公式（2）表示：

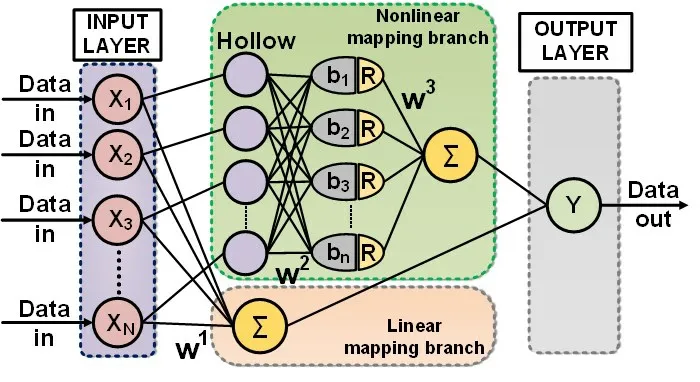
图2 双分支多层感知机后均衡原理图

其中x是DBMLP 的输入向量，其长度N 表示了DBMLP考虑的信号的记忆深度，w1为权重系数，b1是线性映射分支神经元的偏置。

为了降低网络的空间复杂度，DBMLP 主要由线性映射分支来补偿信号的线性失真，而非线性残余分支则主要考虑非线性失真的补偿。在非线性残余分支中，输入数据首先经过一个挖空层（Hol‐low layer)，将数据中间位置的点去掉，可由公式（3）表示：

则非线性残余分支的输出可以表示为：

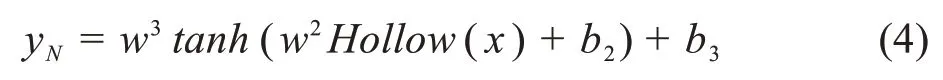
在非线性残余分支中，为了让网络能够模拟非线性噪声，节点激活函数使用tanh，tanh 可由公式（5）表示［7］：

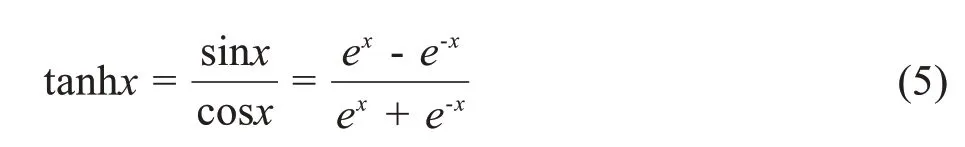
DBMLP的最终输出可以表示为：

2.3 基于时频联合图像分析神经网络的后均衡方法

前述两种神经网络的均衡方法都只是考虑了接收信号的时域特征，然而实验表明，经过均衡后信号的频谱与原始发射频谱仍有一定的区别，所以仅仅考虑信号的时域特征不能完全还原真实的信号。基于时频联合图像分析的神经网络（TFDNet）从图像处理的角度出发，综合考虑信号的时域和频域特性，能够在非线性均衡方面取得更好的效果。

TFDNet的原理框图如图3所示，在将数据输入到神经网络之前，通过短时傅里叶变换（short time Fou‐rier transformation,STFT）联合信号的时域和频域特征，STFT矩阵可以表示为：

图3 时频联合图像分析神经网络后均衡原理图

STFT 矩阵的每一行代表一个特定频率的矢量，由公式（8）表示：

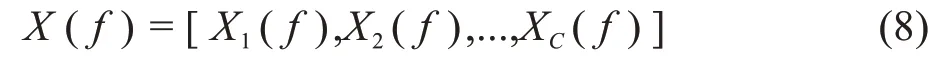
X(f)的第m个元素为

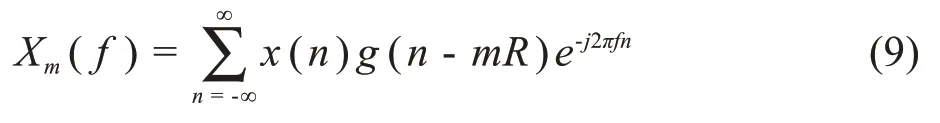
其中g(n)表示长度为K的窗函数，滑窗处理的步长为R=K-L，L表示滑窗后数据重叠部分的长度，在STFT中，对滑窗得到的数据做离散傅里叶变换（dis‐crete Fourier transformation,DFT)。

STFT 矩阵类似于一幅尺寸为2D×的图像，D为DFT 的点数。最后，神经网络的输出是一幅重建后的图像，通过短时傅里叶反变换（ISTFT）可以得到均衡后的信号：

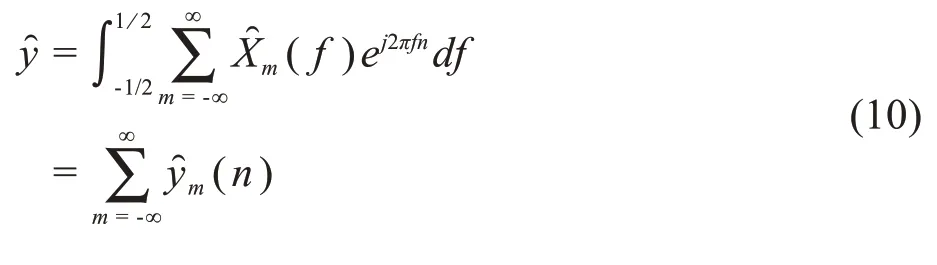
3 基于神经网络后均衡的水下可见光通信系统结构

基于神经网络后均衡的水下可见光通信系统框图及实验装置图如图4 所示。这是一个基于CAP 调制的可见光通信系统，CAP调制的具体过程可参考文献［8］。在发射端，首先对输入的二进制比特流进行QAM 映射，根据编码映射规则将其映射为64QAM 符号；接着对映射得到的64QAM 符号进行IQ 分离，得到相应的同相分量和正交分量；为了匹配CAP成型滤波器的采样率，同相和正交分量进入成型滤波器之前需进行上采样处理，在实验中，上采样倍数设置为4；上采样后的数据通过成型滤波器进行脉冲成型，将两路数据相加即可得到基带传输的实数信号。在实验中，将在MATLAB 生成的数字信号输入到任意波形发生器（arbitrary waveform generator,AWG,Tektronix AWG710B）中产生电信号；为了补偿可见光信道对信号高频分量造成衰减，使用一个单级T 型桥硬件预均衡电路［9］对电信号进行预补偿；均衡后的信号随后经过一个电放大器（electrical amplifier,EA,Mini‑Cir‐cuits ZHL‑6A‑S+）进行功率放大，再通过交直流耦合器（bias tee）调制到LED 上面，产生携带信息的光信号。

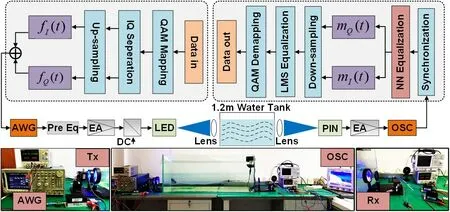
图4 基于神经网络后均衡的水下可见光通信系统框图及实验装置图

实验中用一个1.2 米的水箱模拟水下环境，光信号在水箱中传输，在接收端，通过一个光电探测器（PIN,Hamamatsu S10784）完成光电转换，为了提高接收信号的信噪比，在接收机之前放置一个透镜进行光线汇聚。PIN 输出的电信号由EA 进行功率放大并由数字存储示波器（Digital Storage Oscilloscope,OSC,）采样和量化，以便进行后续的离线数字信号处理。

离线数字信号处理在MATLAB 中进行，首先将接收信号与原始发射信号进行同步，同步后的时域信号通入到神经网络中进行第一级后均衡，神经网络训练的过程中使用一段训练序列作为标签，进行有监督的学习。均衡后的信号相继经过匹配滤波器和下采样后，进行第二级后均衡，此时采用最小均方误差（Least Mean Square,LMS）自适应滤波器以进一步消除符号间干扰。最后，根据编码映射规则，对信号进行解调以获得原始的比特序列，并计算系统的误码率（Bit Error Rate,BER)。

4 实验结果与分析

如图5 所示为系统的AM‑AM 曲线，表示系统响应信号幅度与输入幅度的比值。由图可以发现：幅值的变化不是线性，而是随着幅值的增大呈非线性分布，幅度越大，非线性越大。

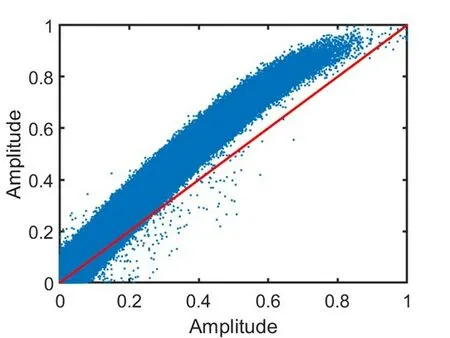
图5 AM⁃AM 曲线

为了更好地衡量可见光通信系统的性能，需要找到系统最佳的工作状态。实验中首先测量了不同LED 驱动电流下系统的误码性能，结果如图6 所示，此时AWG 输出信号的幅度（Vpp）固定为0.7V。可以发现：BER 随着驱动电流的增大先下降后上升，存在一个范围使得系统工作在比较好的状态，当驱动电流比较小时，LED 的发光强度比较小，经过信道传输后，接收端接收到的信号功率比较小，此时信号的信噪比（Signal To Noise Ratio,SNR）比较低，所以误码率比较高。随着驱动电流的增大，LED 进入工作的线性区，此时误码性能逐渐变好。而驱动电流继续增大则会导致LED进入工作的非线性区，给信号引入非线性失真，从而影响系统的性能，BER增大。

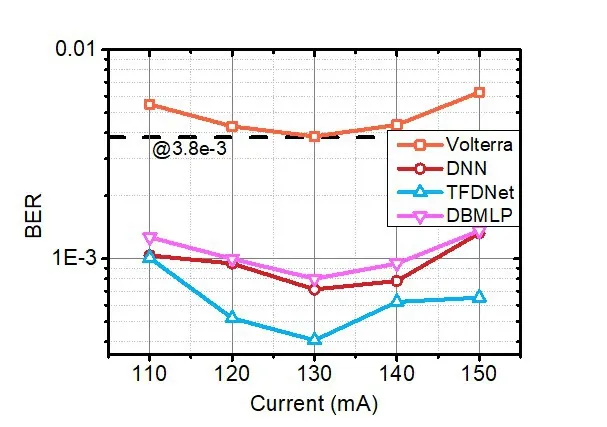
图6 误码率随驱动电流变化关系

实验中比较了采用几种不同均衡方法情况下的误码性能，包括基于Volterra 级数的非线性均衡方法、DNN、TFDNet 和DBMLP。从图中可以看出，采用传统的基于Volterra 级数的均衡方法不足以补偿信号的非线性失真，BER 都在7%前向纠错码（forward error correction,FEC）的误码门限3.8×10‑3以上；而采用神经网络的均衡方法能够完成信号的非线性补偿，使得BER 得到有效的降低。其中，TFDNet 的均衡性能最优，并且系统的非线性越强，均衡的效果越好；而DNN 与DBMLP 的均衡性能相当，在两者都训练充分的情况下，DNN 的均衡效果更好，因为DBMLP 在非线性分支训练的时候没有考虑中心点与周围点的联系。

接着实验测量了不同Vpp 情况下系统的误码性能，结果如图7 所示，此时LED 的驱动电流固定为130mA。可以发现：BER随Vpp的变化趋势与LED驱动电流变化的情况类似，当Vpp 比较小时，接收信号的SNR 比较低，系统的误码性能很差，而且低信噪比不足以支持神经网络完成很好的非线性均衡，均衡效果与Volterra 相当；随着Vpp 的增大，接收信号的SNR增加，BER 开始下降，但是Vpp 增大到一定的程度会给信号引进非线性失真，此时信号被削顶，高电平信号质量恶化，导致误码率上升，这是一个相互制约的过程。可以看到，在SNR 比较高的情况下，神经网络的均衡效果要优于Volterra，并且信号的非线性失真越大，均衡的效果越明显。图7 同时给出了当Vpp 为0.8V 时采用不同均衡方法得到的星座图，可以发现，Volterra 均衡后的星座图比较模糊，反映了比较高的BER；DNN 和DBMLP 均衡后的星座图相对来说比较清晰，且两者比较接近；TFDNet均衡后的星座点最为清晰，BER最低。

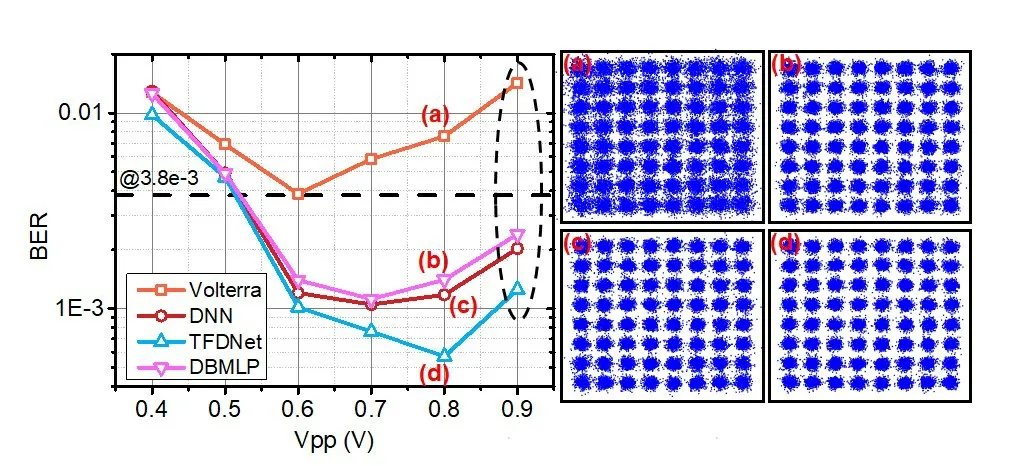
图7 误码率随Vpp变化关系及相应的星座图

接下来，测量了不同传输速率下系统的误码性能，结果如图8 所示。可以发现，当Vpp 为0.7V 时，系统处于最佳工作点，随着传输速率的增加，BER不断上升，使用Volterra 均衡的情况下系统能达到的最高速率为2.92Gbps，而采用神经网络的均衡方法，系统的传输速率能达到3.21Gbps，速率增益为0.29Gbps，说明神经网络的均衡方法给系统带来了性能提升。随着传输速率的增加，通过神经网络均衡带来的增益会变小，因为此时系统处于带宽受限的状态，高频信号的衰减影响了系统的误码性能。当Vpp 为0.9V 时，系统处于强非线性状态，此时使用Volterra 后均衡已不能完成非线性的补偿，不同速率下BER 均高于误码门限，而使用神经网络的均衡方法在3Gbps 传输速率下仍能保证BER 在误码门限以下。

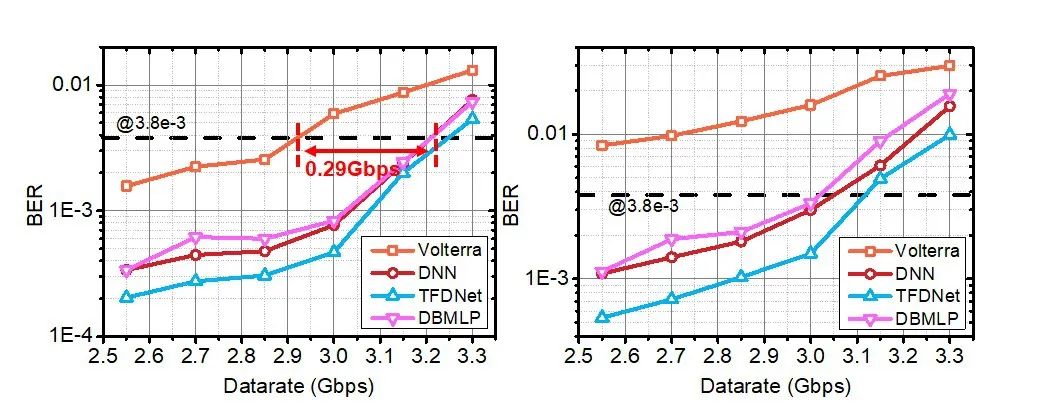
图8 不同Vpp情况下误码率随传输速率变化关系:(a)VpP=0.7V;(b)VpP=0.9V

由图9 可知，可见光信道是一个快速衰落的信道，原始发射信号经过传输之后，高频分量被严重地衰减，这是导致系统误码性能下降的主要原因之一。为了进一步衡量几种不同均衡方法的均衡效果，图10给出了均衡后的频谱图，可以发现，Volterra 后均衡不能很好地完成信号高频部分的补偿，这是导致强非线性下均衡效果不佳的主要原因，而经过DNN 和DBMLP 均衡后的频谱虽然比较接近原始发射频谱，但是相比TFDNet，其在高频处仍有一定的损伤，所以前两者的均衡效果不如TFDNet。TFDNet 在考虑信号时域特性的同时，也把信号频域特性作为学习的参考之一，其非线性补偿的能力要优于DNN 和DBMLP。

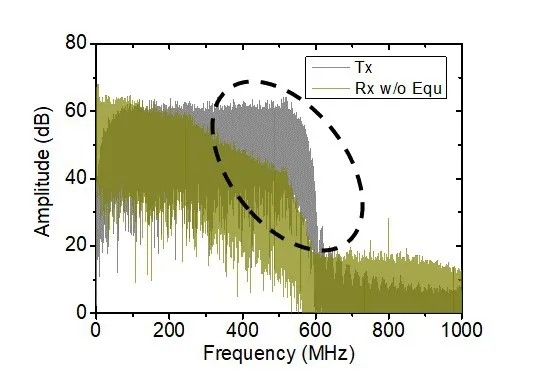
图9 不加均衡情况下的频谱对比

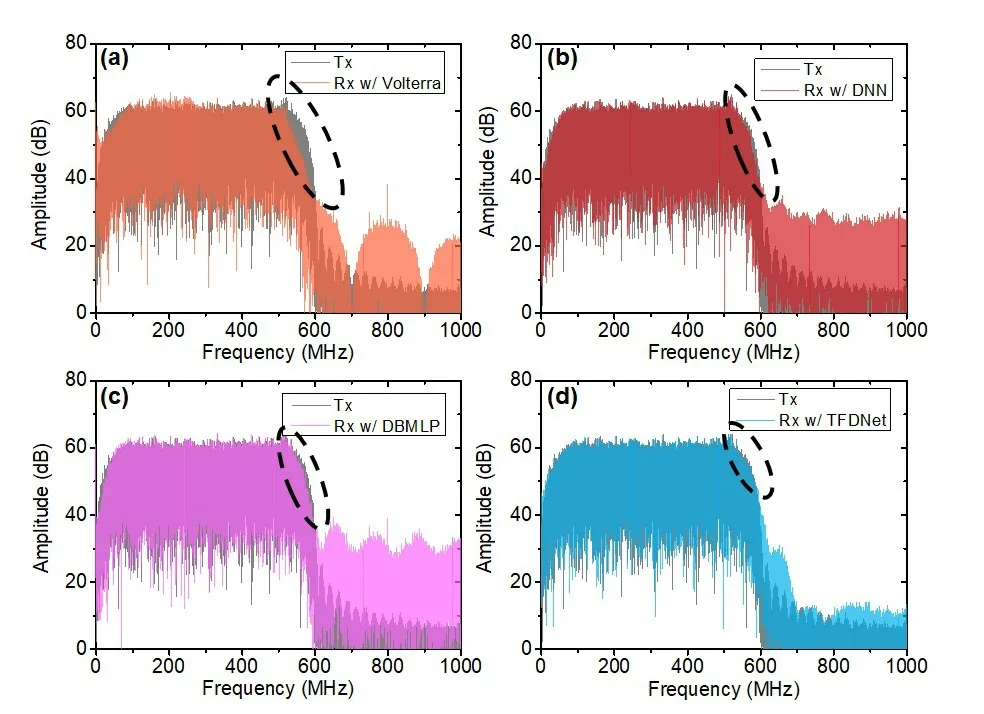
图10 不同均衡情况下的频谱对比

接下来对神经网络均衡方法的复杂度进行比较，用神经网络在训练的过程中需要更新的参数作为衡量的指标，在训练充分的情况下，训练所需更新的参数个数如表1 所示。可以发现，在保证训练充分时，DNN 和DBMLP 的复杂度相当，此时输入节点数为37，隐藏层节点数为100。而TFDNet训练需要更新的参数比较多，输入节点数为48，隐藏层节点数达到256，并且TFDNet 均衡方法中对接收信号进行STFT和ISTFT 也会导致系统的复杂度增加。在不考虑复杂度的情况下，经过TFDNet均衡后的误码性能最佳，可以考虑选择TFDNet来对接收信号进行后均衡。

表1 不同均衡方法训练所需更新参数列表

但是，在复杂度要求比较高的情况下，三种神经网络后均衡得到的效果可能不一样，图11给出了在较低复杂度情况下BER随Vpp变化的关系，此时设置神经网络隐藏层的节点数为30。可以发现，复杂度受限会导致TFDNet和DNN 训练不充分，此时系统的误码性能会下降，而DBMLP 则体现出计算复杂度低的优势，在较低复杂度情况下仍能得到比较好的训练效果，取得比TFDNet和DNN要好的均衡性能。

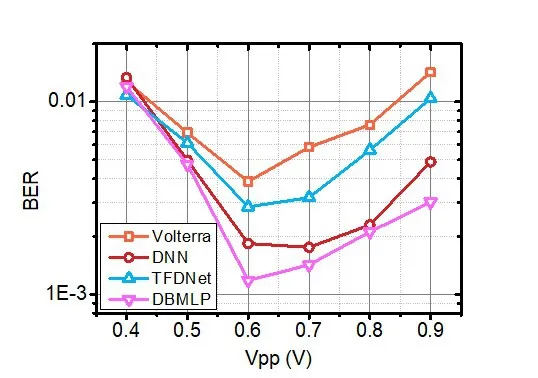
图11 低复杂度情况下误码率随Vpp的变化关系

5 结论

在水下可见光通信中，系统的误码性能受到非线性失真的影响，而神经网络具有解决复杂非线性问题的能力，将其应用在水下可见光通信系统中，可以有效完成信号的非线性均衡。本文介绍了基于神经网络的后均衡方法在水下可见光通信中的应用，从原理出发，通过实验对比分析了DNN、DBMLP和TFDNet三种网络在非线性均衡方面的性能。实验表明，相对于传统的基于Volterra级数的均衡方法，神经网络的均衡方法取得比较大的性能提升。在不考虑计算复杂度、网络训练充分的情况下，TFDNet均衡的效果最优，DNN与DBMLP均衡的性能相当，而当计算复杂度受限时，TFDNet和DNN由于训练不充分导致均衡性能下降，此时DBMLP发挥计算复杂度低的优势，均衡效果最优。