基于长短时记忆算法的热应力下半导体器件故障预测模型

张明宇, 王琦,2, 于洋

(1.沈阳工业大学 信息科学与工程学院，辽宁 沈阳 110870; 2.辽宁工业大学，辽宁 锦州 121001)

0 引言

电子器件在贮存、运输和使用过程中会受到热应力、电应力、环境辐射、机械振动等各种环境应力的影响，当这些应力条件超过最大额定值时，将对其造成损伤。电子器件由应力积累损伤所造成的永久性故障在形式上多表现为突发性、随机性，发生前无明显的外在征兆，给电子器件的状态预测与性能评估带来困难。近年来，通过深入机理分析与大量试验研究，学术界对电子器件耗损规律有了初步认识：虽然电子器件故障的产生具有突发性，但超过负载的环境应力会造成器件参数超过正常容差范围，导致产品状态退化，退化程度和退化速度与器件暴露在环境应力中的面积、持续时间有关[1]，从而为电子器件故障预测和健康管理(PHM)提供了理论依据。

PHM是一种预测性维修策略，是视情维修的支撑技术。目前，PHM技术在机械领域已得到广泛应用，电子设备的PHM技术仍集中在总体架构方面，维修决策管理的研究比较少，未能取得应用于工程实际的实质性突破。美国、英国相关研究起步较早、基础较好，已形成比较成熟的体系架构。我国电子设备PHM技术还处于原理概念的方法论阶段，以跟踪国外研究、借鉴机械类研究为主。

PHM技术的基础和关键是故障预测，但由于电子器件易受多种环境应力影响，器件结构复杂，构建一个确定的故障物理模型较难，目前PHM技术中常用的故障预测方法为数据驱动法，即通过大量历史数据挖掘电子器件状态与环境应力间的潜在联系。数据驱动法又可分为机器学习法和统计数据法。基于机器学习的数据驱动法包括最近邻算法、神经网络法、支持向量机方法等。基于统计数据的数据驱动法包括回归模型法、马尔可夫法、主成分分析方法等。美国马里兰大学Dorj等[2]采用隐式马尔可夫模型研究绝缘栅双极型晶体管(IGBT)的故障预测与健康管理。Kunche等[3]采用滤波算法，以常见滤波器电路作为研究对象，监测电路中元器件如电阻、电容取值的变化，研究电路级的故障预测与健康管理。美国宇航局(NASA)的Saha等[4]通过采用粒子滤波器算法处理实验数据，研究单个IGBT的故障预测与健康管理。我国电子领域的PHM技术研究主体以高校和科研院所为主，研究方法也以数据驱动法居多。北京航空航天大学于格等[5]、查国清等[6-7]、蒋旭等[8]提出基于故障行为模型的电子产品寿命分析方法，通过加速试验获取电子产品失效机理，完成电子产品健康状态评估。电子科技大学龙兵等提出了最小二乘支持向量机模型[9]、加权隐马尔可夫的自回归状态预测模型[10]、贝叶斯网络的故障预测模型[11]以及最小二乘支持向量机-隐马尔可夫模型[12]，用于研究电路的故障预测与健康管理、模拟电路的剩余寿命[13]。国防科学技术大学吕克洪等[14-17]对电子器件故障预测和健康管理技术发展动态进行阐述，分析损伤与时间应力的关系，提出了基于优化自回归模型的电子器件寿命预测方法。此外，席霄鹏等[18]基于维纳过程建立系统性能状态空间模型，描述了测量信息与真实退化之间的关系。张朝龙等[19]应用加权贝叶斯模型对电力变压器进行了故障诊断。樊浩等[20]将主成分分析法与支持向量机法相结合，研究了断路器的故障诊断。

现有研究建立数据驱动模型时，大多只考虑应力等级对研究对象的影响，忽略了应力累计时间对研究对象的作用。本文以电子器件中的半导体器件为研究对象，综合考虑应力等级和应力累计作用时间对研究对象造成的积累损伤，基于长短时记忆(LSTM)算法，充分挖掘研究对象在不同应力等级和应力时长作用下数据特征与影响因素的潜在关系，研究半导体器件状态随热应力和应力累计时长的变化趋势，预测故障时间，以避免对失效机理的过度依赖。

1 热应力、应力累计时长与半导体器件状态关联性分析

1.1 热应力对半导体器件参数的影响

随着现代半导体设计、制造工艺和控制过程技术的发展，半导体器件因工艺造成的早期失效率和偶然失效率已接近于0.时间和环境应力成为引起半导体器件故障的主要外因。

热应力是半导体器件使用过程中常见的环境应力。热应力引起半导体器件故障的失效机理，常见的有热载流子注入效应、电迁移效应、时间相关的电介质击穿效应和因热膨胀系数不匹配引起的器件结构变化。下面简要介绍热应力下半导体器件的失效机理:

1)热载流子注入效应由热载流子(电子和空穴)注入栅氧化层引起。热载流子比热平衡状态下的载流子具有更高的动能，由于载流子具有很高的能量，可在硅-二氧化硅界面处和栅氧化层中产生大量缺陷，从而导致器件退化乃至失效。

2)电迁移效应是在高电流密度作用下，由金属中的原子迁移所致。电迁移会引起金属互连线短路或开路失效，进而影响半导体器件的寿命。

3)时间相关的电介质击穿效应也受热应力的影响。温度的升高会导致栅氧化层薄膜中的共价键更易断裂，电子破坏作用更明显，击穿所需时间缩短，所需击穿电量减少。

4)半导体器件管芯、基板、管壳等部位的材料热膨胀系数不同，当温度快速变化时材料将产生热膨胀和收缩，不同材质交界面处将产生机械应力，最终形成空洞、裂纹，进而影响器件的性能。热膨胀系数的不同，还会使芯片和基板之间的粘接层产生疲劳失效，造成电子器件热性能变差、内部粘接不牢、芯片翘起、热阻增大和功率循环性能变差。

上述失效机理在初始状态下并不会影响半导体器件的正常工作，但随着使用时间和使用频率的增加，器件暴露在热应力中的时间越来越长，器件性能会逐渐退化。热应力对半导体器件性能的影响主要体现在阈值电压、迁移率、漏极电流、延时时间、跨导、漏-源导通电阻RDS(on)和逻辑电平等参数上[21]。

1.2 实验数据分析

由于半导体器件在正常应力水平下寿命可达几十万甚至上百万小时，在预测半导体器件故障及可靠性问题时常采用加速老化实验。此次样本数据采自美国宇航局艾姆斯研究中心提供的金属-氧化物半导体场效应晶体管热过应力老化数据集。在加速老化实验中，温度由常温逐渐上升到预设温度，实验为不同老化温度和实验时长的组合，加速老化实验预设温度及预设温度下的实验时长如表1所示。实验所用半导体器件为IRF520NPbF，数据集中包括栅-源电压、漏-源电压、漏电流和壳温等参数的监测数据。

表1 加速老化实验条件

以数据集中12号器件为例，通过(1)式计算RDS(on)，分析热应力和应力累计时长对半导体器件状态的影响。

(1)

式中：VDS为漏-源电压；ID为漏极电流。RDS(on)随热应力等级和热应力作用时间的变化趋势如图1、图2所示。从图1中可以看出，前4次实验中，相同的老化时长内，RDS(on)参数主要受温度变化的影响，随温度的下降而降低。图2显示，第5次实验中，在壳温低于第4次实验的情况下，器件RDS(on)参数值反而要远大于第4次实验值，此时应力累计时长为影响RDS(on)参数的主要因素。由上述分析可知，RDS(on)参数的变化不仅与热应力等级有关，还受实验累计时长的影响。

图1 前4次实验RDS(on)变化趋势图

图2 第4次实验与第5次实验RDS(on)变化趋势图

综合上述分析可知，研究半导体器件性能的变化，仅考虑热应力等级的影响是不充分的，还应考虑热应力累计时间。本文考虑的半导体失效因素如图3所示：RDS(on)在热应力等级和热应力累计时间的共同作用下发生变化，进而引发产品失效。

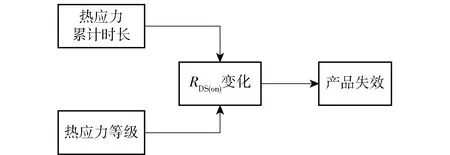
图3 热应力下半导体器件失效原理图

2 热应力下半导体器件故障预测模型研究

2.1 LSTM算法描述

传统的循环神经网络(RNN)通过隐状态存储历史信息，但隐状态每个时刻都会被重写，因此是一种短期记忆。当输入序列很长时，RNN还会出现梯度爆炸和梯度消失问题。

LSTM是应用在深度学习领域的特殊循环神经网络，是对RNN模型的改良，能够建立较长距离的时序依赖关系并有效解决RNN梯度爆炸和梯度消失问题，由Hochreiter与Schmidhuber于1997年提出[22]。

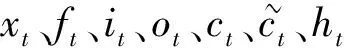
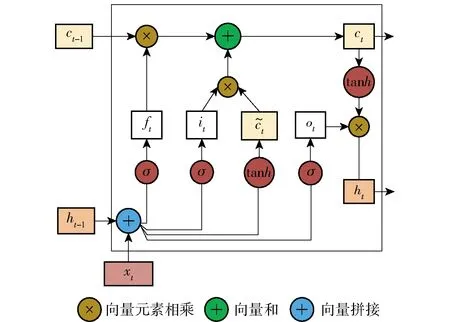
图4 LSTM循环结构单元

设Wxf、Wxi、Wxo、Wxc分别表示xt与遗忘门、输入门、输出门、记忆单元间的权值，Whf、Whi、Who、Whc分别表示隐藏层与遗忘门、输入门、输出门、记忆单元间的权值，bf、bi、bo表示偏置，⊙表示向量元素乘积。LSTM循环结构单元通过控制遗忘门、输入门和输出门的开关程度，控制信息的流动，具体过程如步骤1～步骤6所示。

步骤1遗忘门ft以当前层的输入xt、上一时刻隐藏层的输出ht-1作为输入，遗忘门的输出结果与ct-1相乘，控制上一个时刻的内部状态ct-1需要遗忘多少信息，其表达式见(2)式：

ft=σ(Wxfxt+Whfht-1+bf).

(2)

步骤2输入门选择性地保留当前输入信息，输出结果it作为将要更新的信息，表达式如(3)式：

it=σ(Wxixt+Whiht-1+bi).

(3)

步骤3输出门ot控制当前时刻的内部状态ct有多少信息需要输出给外部状态ht，表达式见(4)式：

ot=σ(Wxoxt+Whoht-1+bo).

(4)

步骤4输出门ot与经过tanh层处理后的记忆单元状态相乘，得到隐藏层的输出ht，见(5)式：

ht=ottanh ⊙(ct).

(5)

步骤5记忆单元ct记录了到当前时刻为止的历史信息，可由(6)式计算得出：

(6)

(7)

2.2 模型架构及训练方法

输出样本R可表示为

考虑到实际采集环境中存在的干扰因素会影响数据的真实性，采用加权滑动平均滤波法滤除样本中的高低频噪音。其基本思想是根据窗口内各项数据的重要性，对近期数据赋予较大的权重[24]，如(8)式所示：

(8)

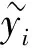
wd=N+1-d.

(9)

实验中的控制信号频率为1 kHz，占空比为40%，5次实验采集的数据量巨大。作为深度学习网络，虽然LSTM算法支持面向底层原始数据直接训练，但此举会造成不必要的重复训练，引发模型收敛困难、预测时间过长等问题。结合实际情况，经综合考虑，选用1阶预测器数据压缩算法剔除重复、冗余数据。具体操作如(10)式～(12)式所示：

Δx(t2)=x(t2)-x(t1)，

(10)

式中：t1、t2表示相邻时刻；x(t1)、x(t2)为t1、t2时刻对应的两个数据点。利用x(t1)和x(t2)定义1条直线，如(11)式和(12)式所示：

(t3)=x(t2)+Δx(t2)，

(11)

(12)

设置一个可变阈值，如果t3时刻采样点在阈值范围内则去除，反之留用。图5、图6分别为原始数据和压缩处理后的数据。对比图5和图6可以看出，压缩后的数据在数据量减少的同时，较好地保留了原始数据的变化趋势。

图5 原始数据

图6 压缩后的数据

由于作为样本的多源数据量纲不同，为避免量纲对模型训练结果的干扰并加快模型收敛，对样本进行归一化处理后再进行模型训练。归一化公式如(13)式所示：

=(x-xmin)/(xmax-xmin)，

(13)

模型初始参数在均值为0、方差为2/(a+b)的均匀分布中抽取，其中a为模型输入数量，b为模型输出数量。模型训练时，采用Adam算法[25]优化LSTM模型权重参数，具体步骤如下：

步骤1划分训练样本集与测试样本集。

步骤2设置LSTM模型初始化参数、学习率。

步骤3没有达到停止准则前循环执行第1步～第6步：

1)m个样本批量输入LSTM模型中，y为样本对应的目标输出，进行前向传播计算；

2)进行反向传播计算，计算梯度：

3)t←t+1；

4)计算有偏1阶矩估计：

s←ρ1s+(1-ρ1)g；

计算有偏2阶矩估计：

r=ρ2r+(1-ρ2)g⊙g；

5)计算1阶矩的偏差：

计算2阶矩的偏差：

6)进行权重参数更新：

如果达到停止准则，则停止执行，否则返回第1步。

步骤3中：g为梯度；L(·)为损失函数；θ为初始参数；x(i)为数据集的第i个样本输入，y(i)为对应目标；ρ1、ρ2为矩估计的指数衰减率；s为1阶矩变量；r为2阶矩变量；ε为步长；δ为分母偏移量。

3 实验验证与分析

为了检验本文所提基于LSTM算法的热应力下半导体器件故障预测模型，用金属-氧化物半导体场效应晶体管热过应力老化数据集的实验数据进行验证。选取8号、9号、11号和14号IRF520NPbF的实验数据作为训练集进行训练，12号IRF520NPbF的实验数据作为测试集进行预测验证，训练集和测试集的划分如表2所示。

监测的原始序列数据包含噪音，首先用加权滑动平均滤波法进行平滑处理。由于实验是对器件的全寿命周期进行不间断监测，数据量巨大，为了在海量时域监测信号中提取状态变化趋势，也为了加快模型收敛速度，对滤波后序列数据进行压缩处理以剔除冗余数据，压缩后的数据量如表2所示。为消除因多源数据量纲不统一对模型预测结果造成的影响，进行压缩后的数据归一化处理，将数据大小限定在[0,1]范围内。

训练集和测试集经预处理后，结合1.2节的实验条件训练故障预测模型，以探究热应力等级和应力累计时长对半导体器件的影响情况。在此阶段，将训练集中的壳温及应力累计时长输入LSTM网络模型中，以真实RDS(on)值作为模型输出，训练热应力下半导体器件LSTM故障预测模型。从表2中可观察到，压缩后的全寿命序列数据量依然很大，而LSTM独特的门控机制与引入的记忆单元，使之处理这类较长的输入序列时，也可以学习当前时刻为止的所有历史信息,建模这种长距离的依赖关系。模型采用堆叠结构，初始学习率设为0.01，选用Adam方法优化权重参数。经实验，迭代次数设为1 500，dropout值设置为0.5.模型使用半均方误差作为损失函数，其表达式如(14)式所示：

表2 实验数据

(14)

式中：S为样本个数；Q为样本中真实值的数量；Tij为模型预测值；Yij为样本真实值，即模型目标值；5次实验的损失函数曲线如图7所示。为更明显地显示损失函数曲线的变化趋势、清晰地反映曲线细节，图7中的损失函数值为对数值。从图7中可以看出：5次实验的模型损失函数经1 500次迭代后，均已收敛；收敛后损失函数的对数值集中在[-2.9,-2.7]范围内，对应着损失函数值范围为[0.001,0.002]。

图7 LSTM模型损失函数曲线图

图8～图12分别为表1中5次实验的模型输出结果。从5次实验的加速老化时长，可推算出5次实验的加速老化累计时间为35 min、70 min、105 min、140 min和320 min.从图8～图12中可以看出，模型预测值曲线和目标值曲线具有很好的吻合度。

图8 第1次加速老化实验预测结果(预设温度250 ℃，老化时长35 min)

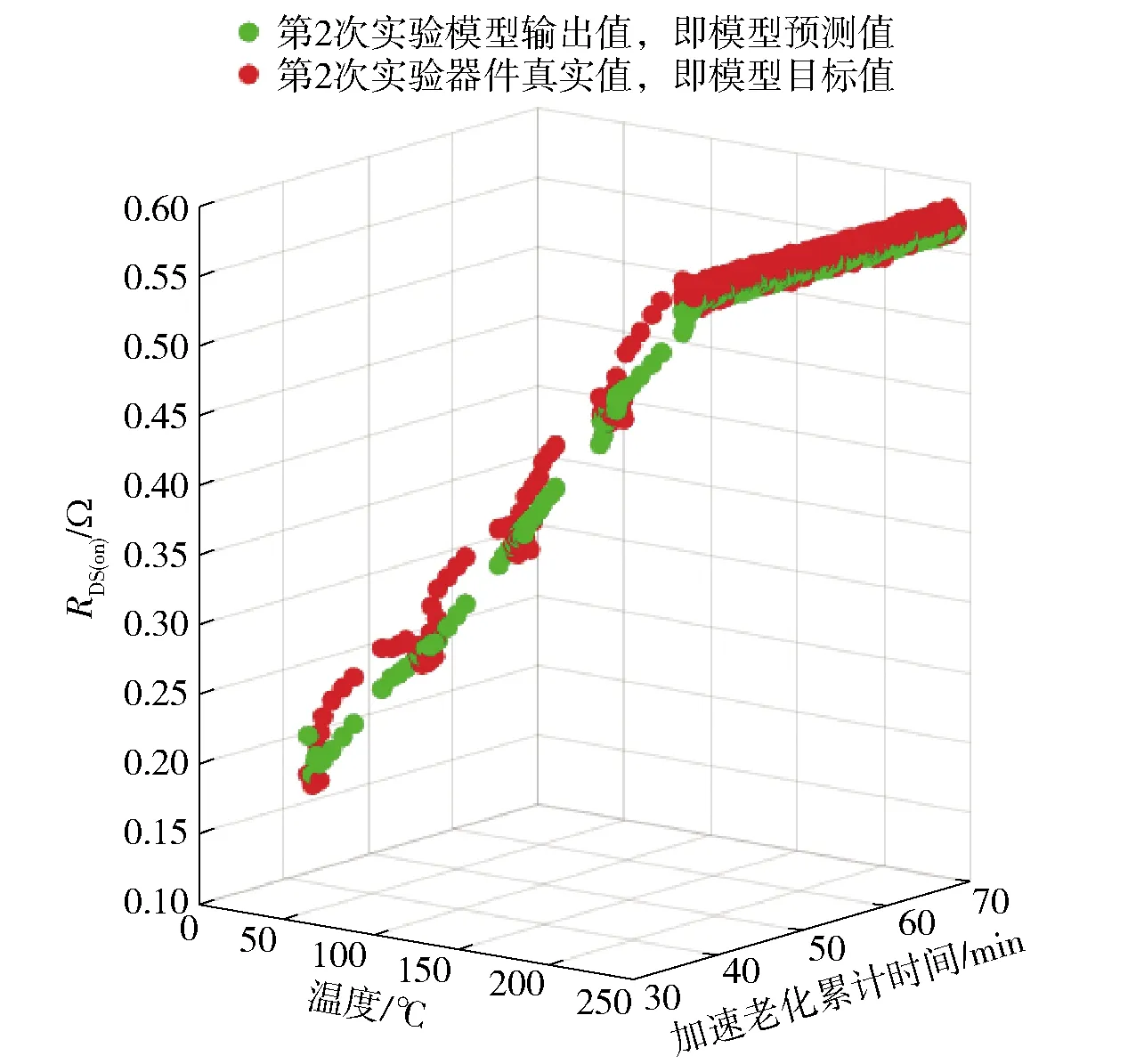
图9 第2次加速老化实验预测结果(预设温度240 ℃，老化时长35 min)

图10 第3次加速老化实验预测结果(预设温度230 ℃，老化时长35 min)

图11 第4次加速老化实验预测结果(预设温度220 ℃，老化时长35 min)

图12 第5次加速老化实验预测结果(预设温度210 ℃，老化时长180 min)

对比观察图8～图12的模型输出曲线可以发现，相对于前4次实验RDS(on)的缓慢增长，第5次实验RDS(on)的增长开始加快，在210 min左右RDS(on)开始激增，而模型输出曲线也很好地反映了这一变化趋势。在壳温稳定在实验预设温度后，选取RDS(on)参数20%的漂移作为器件故障阈值[26]。仍以12号器件为例，用模型预测值计算RDS(on)参数的漂移情况，具体数值如表3所示。

从表3中可以看出，前4次实验RDS(on)参数的漂移低于故障阈值，可判断器件并没有发生故障，这也与真实实验结果相符。RDS(on)参数在第5次实验中漂移超过故障阈值，计算故障时间如表4所示。

表3 RDS(on)参数漂移百分比

表4 预测故障时间与实际故障时间

从表4中可以看到，12号器件在实验累计进行265 min时发生故障，模型预测故障在227 min时发生，模型能够提早预测故障的发生，具有合理性。

为了更直观地反映基于LSTM法建立的多源数据模型对半导体器件状态预测的优势和建立的故障预测模型的可信度，使用均方根误差作为模型评价标准，均方根误差越小，表示模型回归预测效果越好。

将多源数据LSTM模型的均方根误差分别与单以壳温为输入的LSTM模型、多源数据反向传播(BP)神经网络模型均方根误差对比，如表5所示。从表5中可以看出，本文建立的基于LSTM算法的多源数据模型均方根误差最小，曲线拟合度最好。

表5 模型的均方根误差

用更直观的点线图表示各模型均方根误差，如图13所示。从图13中可以看出：5次实验中，单以壳温为样本输入的LSTM模型均方根误差大于本文建立的多源数据LSTM模型，表明同等条件下将应力等级和应力累计时长同时作为样本输入，可提高模型的准确率，验证了本文方法的有效性；第5次实验时，壳温LSTM模型的均方根误差尤其大，这一现象也印证了前文的分析，即第5次实验中应力累计时长是影响器件性能的主要因素，而壳温LSTM模型在建模时只考虑了热应力的等级，忽略了应力累计时长对器件的影响，因此此次预测准确率降低，验证了建模时同时考虑应力等级和应力累计时长的合理性及多源数据LSTM模型的优越性。

图13 各模型均方根误差对比

虽然BP神经网络法也支持建立多源数据模型，但从图13中可见，BP神经网络法构建的5次实验模型均方根误差均大于LSTM法构建的模型，且BP神经网络法的均方根误差随着实验累计时长的增加而增长。由此可见，LSTM算法具备长期记忆的特征，使之处理半导体器件这类现状态与之前时刻状态有关的长序列问题时更具优势，此方法5次实验的模型输出曲线与目标值曲线几乎重合，走势一致，输出结果和目标值吻合度较高，可以较好地拟合热应力作用下样本参数的变化趋势，模型的计算结果作为预测值可信度高。

4 结论

本文以LSTM法为基础，利用LSTM长期记忆的能力有效地建立了热应力、应力累计时长与半导体器件状态间的逻辑关系。得到主要结论如下：

1)本文所提方法与多源数据BP神经网络法、单以壳温为输入的LSTM法进行对比，通过表5的数据可以看出，本文所提方法预测误差最小，表明本文所建立的模型输出结果与目标值吻合度最高，能够良好地预测研究对象的状态发展趋势。

2)根据模型输出值与阈值的关系，预估研究对象故障时间。通过表4可以看出，模型能够提早预测故障的发生，验证了该方法的有效性和合理性，表明此方法是可以工程推广的。