RLV再入段模糊NLPID抗干扰控制器设计
王 佳 曾庆华
中山大学航空航天学院,广州 510006
0 引言
RLV再入段依靠气动栅格舵减速,飞行速度变化剧烈、模型参数不确定和强非线性对RLV姿态控制系统提出了更高的要求。
增益调度法[1-2]采用PID控制设计各个特征点的控制参数,PID控制调节参数少,便于分析,在工程上得到广泛应用;由于再入段气动环境复杂,存在各种干扰,PID控制无法保证良好的姿态控制效果,甚至造成火箭失稳。自抗扰控制器(Active Disturbance Rejection Control,ADRC)由跟踪微分器[3]、非线性误差反馈和扩张状态观测器构成,其非线性结构弥补了PID控制器的不足[4],在航空航天领域取得了较多的研究成果。为解决导弹的模型不确定问题,文献[5]研究了基于自抗扰观测器频带特性的参数整定方法,提升了系统的抗干扰和跟踪性能;文献[6]研究了运载火箭经过大风区的减载控制问题,改进了自抗扰控制律来区分干扰构成,提高了增益的选择范围和控制效果。针对高超声速飞行器再入过程的参数不确定问题,文献[7]利用ADRC跟踪阻力加速度剖面,在模型参数摄动时能够保证较好的系统响应。扩张状态观测器对误差的估计和补偿效果直接影响控制系统的性能,而ADRC控制参数多,对火箭的姿态控制器也带来了一定的困难。NLPID控制器[8]与ADRC相比不含扩张状态观测器,控制参数少且易于工程实现,控制性能优于PID控制器。文献[9]研究了NLPID控制器在级联控制系统的应用,验证了NLPID和PID的6种级联组合对系统的影响,这对火箭角度环和角速度环的级联系统设计具有指导意义。文献[10]设计了6个NLPID控制器用于六自由度无人机的位置和姿态控制,系统的稳态误差和响应速度均优于PID控制器。
进入21世纪,人工智能的研究热度越来越高,神经网络、模糊控制、遗传算法等在导弹控制系统已经取得了很多研究成果[11]。模糊控制对外界扰动和参数摄动的适应能力强[12],文献[13]针对高超声速飞行器气动参数变化引起的不确定性问题,设计了模糊分数阶PID控制器,分数阶运算保证了系统的控制精度和稳定性,模糊控制增强了系统的鲁棒性;考虑到某导弹飞行时存在干扰和参数摄动问题,文献[14]基于变论域理论设计了变论域模糊PID驾驶仪,通过引入伸缩因子来实时改变输入输出论域,在干扰条件下,仿真表明该驾驶仪具有良好的抗干扰性能。考虑到导弹控制系统参考模型不精确和非线性时变的特点,文献[15]利用模糊控制器的在线推理能力整定PID控制器参数,为了进一步提高系统性能,采用遗传算法整定模糊控制参数集参数,结果表明,该控制器具有良好的鲁棒性和实时性。但是遗传算法优化需要设置合理的目标函数和种群规模才能获得比较理想的寻参效果,参数整定时存在效率低和结果不稳定的缺陷。文献[16]设计了模糊自适应姿态控制策略,为提高模糊推理的实时性,采用扩张状态观测器观测角速率动态中的参数摄动和外界扰动,仿真表明,该策略能够很好地跟踪高超声速飞行器的姿态角指令。
上述研究大多未考虑飞行振动和随机风扰动问题,这些问题会对模糊PID控制的推理过程产生不利影响。本文采用新型跟踪微分器,提高了NLPID控制器的抗干扰和滤波能力,使攻角误差及其微分更加稳定;随后总结了控制参数影响系统响应速度、超调量和稳态误差的规律,根据系统实时反馈量调节控制参数,为进一步设计自适应控制器提供了基础;为了提高火箭抑制动力学模型参数摄动和抗干扰能力,引入模糊控制并改进模糊规则以提高NLPID的自适应能力,根据系统反馈的攻角误差量及其微分实时调整跟踪微分器的速度因子和NLPID的增益参数。仿真结果表明:本文设计的模糊NLPID控制器能够有效抑制参数摄动和外界干扰,提高模糊推理的可靠性。
1 RLV姿态动力学模型
为了简化RLV数学模型,有如下假设:1)RLV为一刚体,质量不变;2)气动外形对称。将RLV模型解耦为3个通道,包括俯仰、偏航和滚转通道,火箭无滚转运动。姿态控制回路分别跟踪制导回路产生的攻角和侧滑角[17],基于上述条件,可得火箭再入段姿态运动模型:
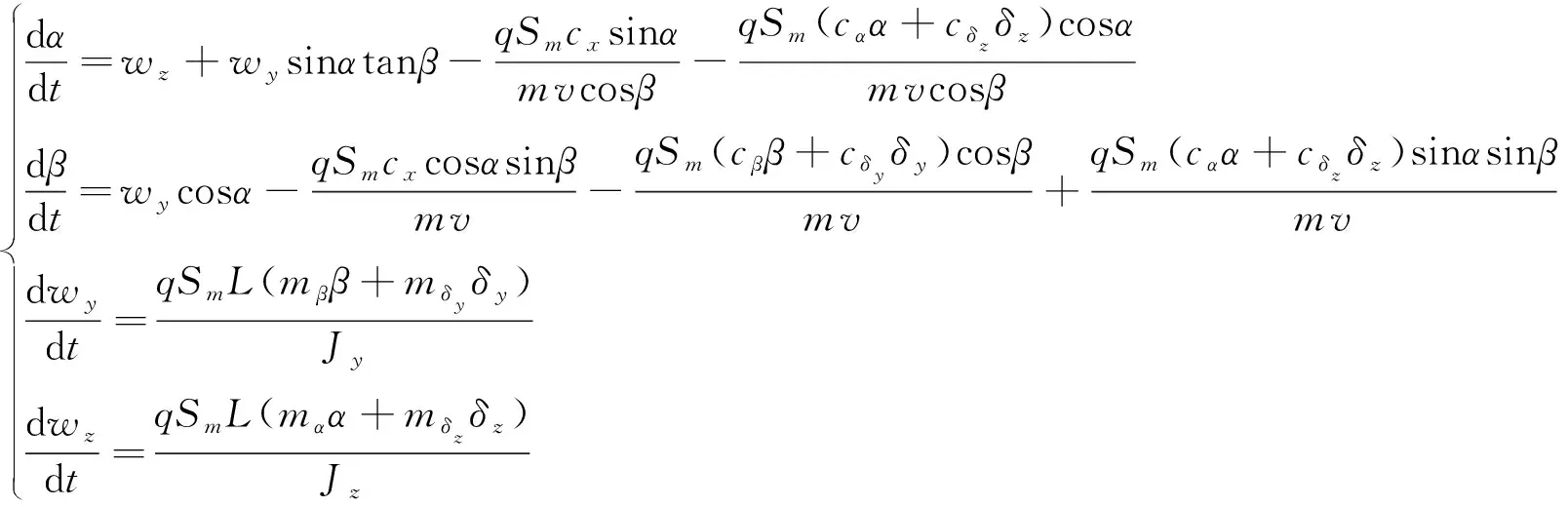
(1)
式中:α,β,wz,wy,δz和δy分别为攻角、侧滑角、俯仰角速度、偏航角速度、俯仰舵偏和偏航舵偏,Jz,Jy为转动惯量,cα,cβ,cδz和cδy为气动力对α,β,δz和δy的气动系数,mα,mβ,mδz和mδy为气动力矩对的α,β,δz和δy气动系数,cx为气动阻力系数,Sm为特征面积,q为动压,v为火箭飞行速度,m为导弹质量,L为气动弦长。
2 模糊NLPID控制器设计
火箭姿态控制总体方案见图1。火箭俯仰通道和偏航通道存在耦合,为便于姿态控制器的设计,需将两通道进行解耦,分别设计出两通道的控制器后,再进行耦合模型的仿真验证。后文以俯仰通道的姿态控制器设计为中心展开。图2给出了火箭纵向通道的控制系统框图。

图1 火箭姿态控制总体方案

图2 俯仰通道姿态控制系统框图
为了保证火箭跟踪角速度和姿态角指令的快速性和平稳性,本文的角速度环和角度环均采用了NLPID控制器,角速度环NLPID控制器参数固定,姿态角环NLPID参数通过模糊控制实时改变。
2.1 NLPID控制器结构
图3为模糊NLPID控制器结构图,包括模糊控制器和NLPID控制器2部分,模糊控制器采集攻角跟踪误差及其微分,由知识库和规则库推理得到修正量kr和Δb1;修正量与NLPID原有控制量r和b1经过数学运算,计算得到舵偏控制量δz。模糊NLPID控制器的设计步骤为:1)先设计NLPID,与火箭姿态模型构成闭环,调节控制参数,总结控制参数和控制指标的关系;2)为提高控制器的抗干扰能力和鲁棒性,设计改进模糊控制器,在线整定控制参数,得到模糊NLPID控制器。

图3 模糊NLPID控制器结构图
图3的虚线框内部结构给出了NLPID控制器跟踪目标指令的原理。其中,v表示需要跟踪的目标信号,v1和v2表示过渡信号及其微分信号;e1和e2为误差信号;u为系统输入,y(k+1)和y(3)为系统输出y(k)的跟踪信号及其微分。
1)跟踪微分器
将文献[18]的跟踪微分器引入NLPID控制器。系统输出y(k)经过跟踪微分器得到其跟踪信号y1(k)和微分信号y2(k),为消除y2(k)的震颤,经过fal(·)函数滤波得到新的微分信号y3(k);将新的微分信号y3(k)向前预报λ1时间可得新的跟踪信号y(k+1)。该跟踪微分器可以减少微分信号的震颤,调节跟踪信号的幅值和相位,其离散形式可表示为:
(2)
式中:T,h和r分别为积分步长、滤波因子和速度因子,函数fhan(·)、函数fal(·)和其他变量含义参考文献[18]。
速度因子r对控制性能的影响:r越大,跟踪速度越快,当r大于临界值时,继续增大r对系统影响微弱,r大于临界值,系统易产生超调;r越小,跟踪速度越慢,但是可以抑制系统的超调。通过参数整定,考虑系统的快速性和抑制超调能力,火箭纵向通道r的修正量取为[0.001,1]。
2)非线性误差组合
非线性误差组合的输入为误差信号e1和e2,输出为误差信号的非线性组合,比PID的线性误差组合控制效果更佳。不同的非线性误差组合方式与跟踪微分器组合,可以构成NLPD、NLPI和NLPID等常见非线性PID结构。经仿真验证,因NLPD缺少积分环节,使系统存在较大的静态误差,所以本文采用NLPID形式。
(3)
式中:u0为控制器的输出,b0,b1和b2为控制参数,fal(·)函数定义参考文献[8]。
控制参数b0,b1和b2对系统性能的影响:b0主要影响系统的稳态误差,选择合适的参数可以减小甚至消除系统的稳态误差;b1主要影响系统的响应速度;b2加快了系统的调节速度,有助于减小超调和振荡,提高了系统的动态特性。通过参数整定,得到b1的修正量为:[0,1],b0、b2为定值。
根据上文总结的r,b1对系统的影响,可得r,b1与系统实时误差及其微分的对应关系,为模糊控制器的设计提供依据。
2.2 改进模糊控制器
对火箭气动系数拉偏和施加干扰时,系统可能会出现超调过大甚至发散,采用固定控制参数的NLPID控制器无法满足火箭再入段环境复杂和抗干扰的需求,因此本文采用改进模糊控制器对NLPID的控制参数进行在线整定。
模糊控制器包括知识库和规则库,知识库反映了输入变量和输出变量的隶属度函数,再经过规则库的推理得到修正量。常见知识库建立系统误差e及其微分ec的隶属度函数,经过规则库推理得到控制参数Kp,Ki和Kd。如图4所示,模糊NLPID控制器的输入变量为攻角误差e及其微分ec,输出变量为kr和Δb1。

图4 模糊控制推理过程
1)知识库
e和ec是模糊控制的输入变量,kr和Δb1是模糊控制的输出变量。它们的语言变量分别为E,EC,KR和B1;设定其论域为E:{-2,2},EC:{-4,4},KR:{0.001,1},B1:{0;1}。将{NB,NS,ZO,PS,PB}设置为输入变量和输出变量的模糊子集。
2)规则库
根据前文速度因子r和增益b1对系统性能的影响规律,以及文献[19]的参数整定规则,确定火箭纵向通道的模糊控制规则,见表1。
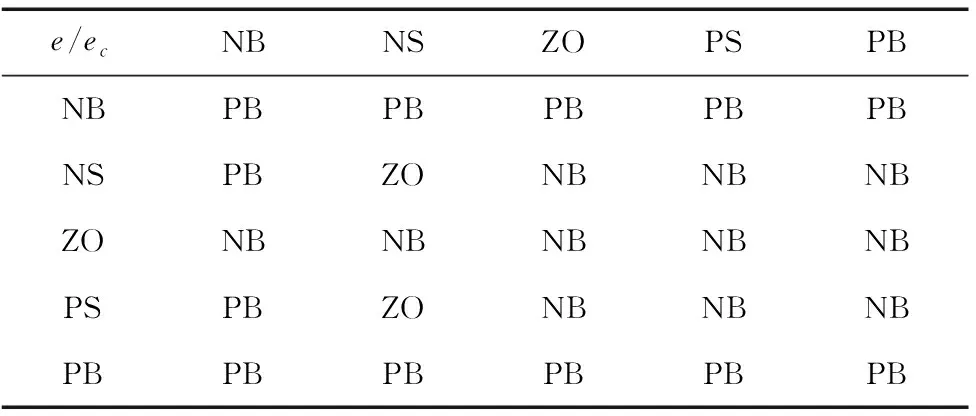
表1 Δb1的模糊规则表
速度因子r的规则库比较简单,为了提高姿态控制器的实时性,本文根据系统的当前状态,采用s-function实现修正量kr的实时更新。
3)模糊控制器输出计算
模糊推理得到的模糊量经过清晰化,可得到实际控制量,采用重心法计算得到模糊控制器的输出Δb1,以模糊输出量B1为例展示清晰化的计算过程:
(4)
式中:n表示B1的规则数目,Δb1为模糊控制器输出量清晰化后的精确值;B1i为模糊控制量论域内的值;μv(B1i)为B1i对应的隶属度值。
可得模糊NLPID控制器更新后的控制参数为:
b1(k+1)=Δb1+b1(k)
(5)
式中:b1(k)是模糊NLPID控制器k时刻的参数,b1(k+1)是经过模糊控制器输出更新后的值。
3 仿真校验
以某火箭再入段气动数据为例,取一特征点的飞行速度、飞行高度、马赫数、大气密度、质量进行仿真。仿真计算软件环境:Win10 64 bit操作系统、MATLAB;硬件环境Intel Corei7-7700处理器、16.0 GB RAM。
3.1 NLPID控制器仿真验证
为了验证NLPID控制器的有效性,分别在不同条件下与PID进行仿真对比,评价指标为调节时间tr和超调量σ。为下文描述方便,将3种仿真条件表述为:条件1:无干扰;条件2 ∶0.8倍Cmz,1.2倍Jz;条件3 ∶1.2倍Cmz,0.8倍Jz。
保证条件1时NLPID控制器和PID控制器的tr和σ相同。保持控制参数不变,由图5知,在条件1和3时,NLPID控制器的tr和σ分别为0.6s和0; PID控制器的tr和σ分别为0.8s和0。可见PID控制器在控制参数固定时,系统响应随气动系数偏差变化更大,而NLPID有着更好的稳定性。

图5 PID和NLPID仿真
继续给系统输出的攻角叠加随机噪声,得到NLPID和PID控制器的攻角响应及其微分的曲线,如图6和图7所示。

图6 叠加噪声系统响应
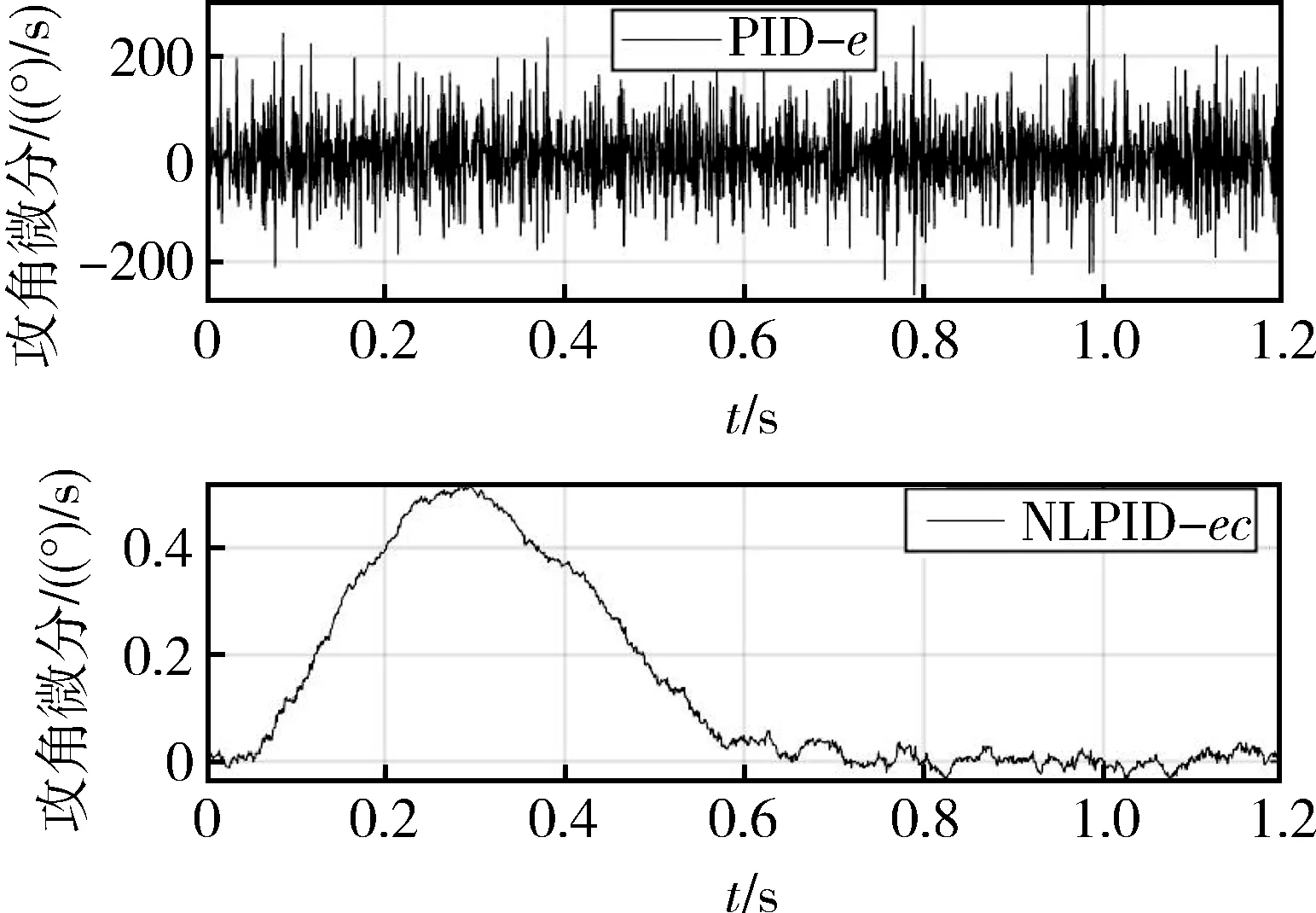
图7 叠加噪声系统响应微分信号
由图6和图7可知,PID控制器由于噪声干扰使攻角及其微分信号产生较大震颤,模糊控制的输入为攻角误差e及其微分ec,较大的震颤不利于系统的稳定;NLPID经过跟踪微分器的滤波作用,大幅降低了震颤。
图8为条件1下的NLPID仿真结果,增益不变时,速度因子r越小,抑制系统超调量的能力越强。利用此特性,可根据系统状态适当调节速度因子r,达到调节系统超调量和快速性的目的。

图8 不同速度因子r时NLPID仿真
3.2 模糊NLPID控制器仿真验证
由图9和图10知,在气动参数摄动时,在模糊NLPID控制器作用下,系统需0.5s进入稳态,响应速度优于模糊PID控制器。

图9 不同条件模糊PID仿真

图10 不同条件模糊NLPID仿真
当存在风干扰,空气流相对于导弹有附加的速度,形成附加的攻角因而产生附加的空气动力和空气动力矩。为了简化模型并验证控制器的性能,将随机风干扰[20]对火箭的影响转换成附加攻角,引入模型中进行风干扰仿真验证。考虑到风干扰和RLV振动对系统的影响,附加攻角采用Simulink的Band-Limited White Noise模块产生,最大值为0.2°。
图11给出了存在随机风干扰时的系统响应曲线,发现系统进入稳态后均存在小幅的波动,但在模糊PID作用下系统始终存在无法消除的稳态误差。
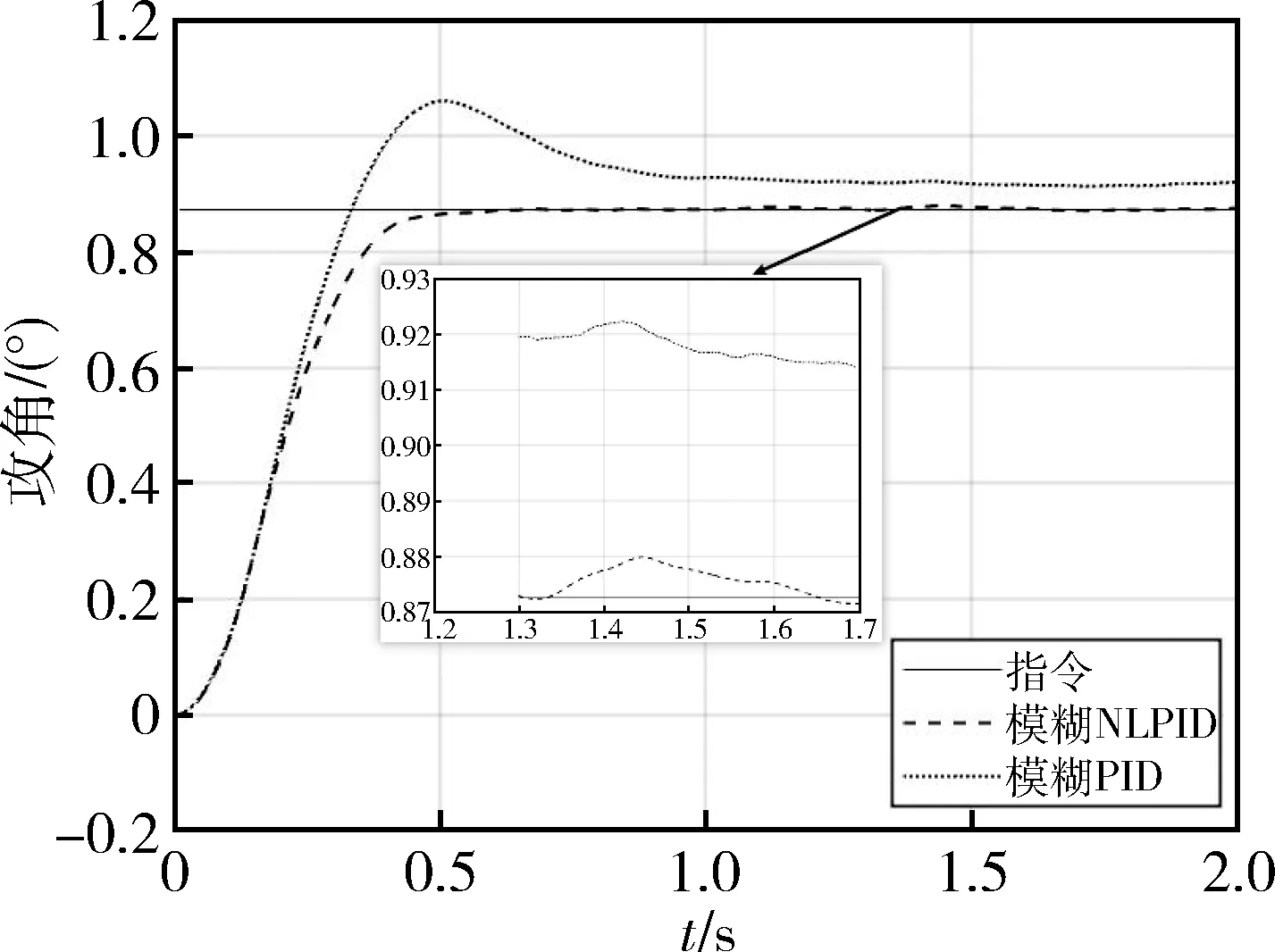
图11 随机风干扰响应
图12给出了速度因子r抑制超调的过程,根据系统当前的状态实时改变速度因子r的值,达到降低超调量的目的。

图12 速度因子r抑制超调
4 结论
结合了NLPID控制器和模糊控制自适应调整的优势,将所设计的改进模糊NLPID控制器应用于RLV再入段的姿态控制。仿真结果表明:该控制器能够有效克服气动系数偏差和环境干扰,系统能够保证较好的鲁棒性和自适应能力;与传统的模糊PID相比具有更好的控制性能,展现了较好的工程应用前景。

