环Fpm[u,v]/〈u3=u,v3=v,uv=vu〉上的常循环码

孔 波， 徐明洁

(1.河南财政金融学院 统计与数学学院，河南 郑州 450046； 2.河南财政金融学院 计算机与信息技术学院，河南 郑州 450046)

0 引言

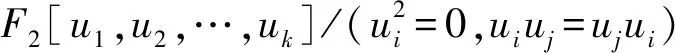
1 基础知识

环R上的理想I如果只有一个生成元， 则称之为主理想。 如果环R的所有理想都是主理想, 则称R为主理想环。如果R有唯一的极大理想称R为局部环。 如果R的所有理想按包含关系形成一条链, 则称之为链环。

令R=Fpm[u,v]/〈u3=u,v3=v,uv=vu〉,易知该环是Frobenius环，不是局部环。

R上长为n的线性码C是Rn的一个R子模。

令

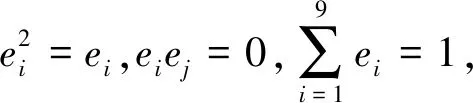
由中国剩余定理可知R=e1R⊕e2R⊕…⊕e9R=e1Fpm⊕e2Fpm⊕…⊕e9Fpm。

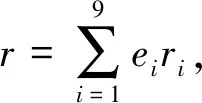
设C为R上的长为n的线性码,则C可以唯一地表示为C=e1C1⊕e2C2⊕…⊕e9C9，其中Ci为Fpm上的线形码，i=1,2,…,9。

设σλ表示R上的一个λ-常循环移位, 即∀(c0,c1,…,cn-1)∈Rn, 都有σλ(c0,c1,…,cn-1)=(λcn-1,c0,c1,…,cn-2)。

设C为R上的长为n的线性码, 若∀(c0,c1,…,cn-1)∈C, 均有σλ(c0,c1,…,cn-1)=(λcn-1,c0,c1,…,cn-2)∈C, 则称C为环R上长为n的λ-常循环码。

∀a=(a0,a1,…,an-1)∈Rn，a的Hamming重量定义

wtH(a)=|{i|ai≠0,i=0,1,…,n-1}|，

码C的Hamming距离定义为

dH(C)=min{dH(a,b),a,b∈C,a≠b},

这里dH(a,b)=wtH(a-b)是元素a,b之间的Hamming距离。

2 Gray映射

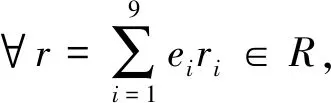
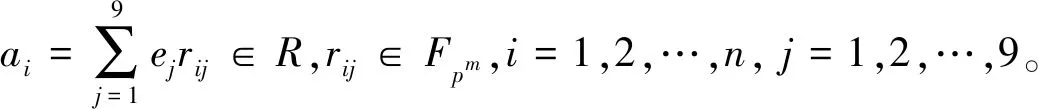
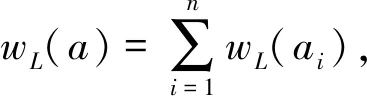
dL(a,b)=wL(a-b)，

则线性码C的李距离定义为

dL(C)=min{dL(a,b),a,b∈C,a≠b}。

由Gray映射定义，易得下面的定理。

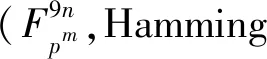
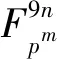
(r1,r2,…,r9)+(r′1,r′2,…,r′9)=φ(a)+φ(b),

所以φ线性的。 由φ是双射可知|C|=|φ(C)|，由定理1，可得dH=dL。

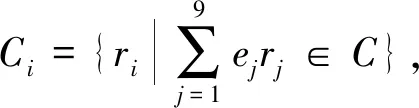
定理4设C为R上的长为n的线性码,若C是自正交的, 则φ(C)也是自正交的。

3 环R上的常循环码

引理2如果C=e1C1⊕e2C2⊕…⊕e9C9为R上的线性码, 则C为R上的e1r1+e2r2+…+e9r9-常循环码当且仅当Ci为Fpm上的ri-常循环码，这里为e1r1+e2r2+…+e9r9上的可逆元。

C为R上的e1r1+e2r2+…+e9r9-常循环码当且仅当

当且仅当σri(ai)∈Ci，即Ci为Fpm上的ri-常循环码，i=1,2,…,9。

定理5若C=e1C1⊕e2C2⊕…⊕e9C9为R上长为n的e1r1+e2r2+…+e9r9-常循环码，则存在g(x)∈R[x]且g(x)|xn-(e1r1+e2r2+…+e9r9), 使得C=〈g(x)〉。

证明若C=e1C1⊕e2C2⊕…⊕e9C9为R上长为n的循环码，设Ci的生成多项式为gi，i=1,2,…,9，则

C=〈e1g1(x),e2g2(x),…,e9g9(x)〉。

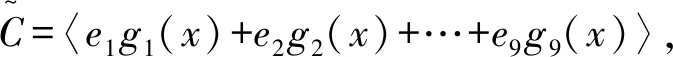
由ei(e1g1(x)+e2g2(x)+…+e9g9(x))=eigi(x)，可得C⊆C′。所以C=C′，且C可以由一个多项式生成。

由gi为Ci的生成多项式gi可知gi(x)|xn-ri。设fi(x)∈Fpm且满足gi(x)fi(x)=xn-ri，则

所以g(x)=e1r1+e2r2+…+e9r9, 定理5得证。

4 结论

本文根据Gray映射建立Fpm[u,v]/〈u3=u,v3=v,uv=vu〉上的常循环码与Fpm上线性码之间的对应关系,证明了环Fpm[u,v]/〈u3=u,v3=v,uv=vu〉上的常循环码是主理想生成的。