基于样本熵的高水头混流式水轮机稳定性分析

朱国俊 陈旻甲 冯建军 刘可然 罗兴锜

(1.西安理工大学水利水电学院， 西安 710048； 2.浙江富安水力机械研究所， 杭州 311121)

0 引言

效率、空化数和稳定性是评价水轮机水力性能的三大指标[1]。其中，稳定性是水轮机乃至电站能否正常运行的主要判据。水轮机的振动或流道内的压力脉动信号是机组稳定性的外在表征[2-3]，研究水轮机各测点压力脉动特征可为水轮机失稳水力根源研究提供可靠依据。

目前，关于水轮机内部压力脉动特性的研究较多。如文献[4]总结了国内外在混流式水轮机尾水管涡带振动机理方面的研究成果；文献[5]将空腔危害水力机械稳定性的理论应用于水轮机间隙空化研究，论证了间隙空化和高倍频压力脉动的关系；文献[6]以国内某水电厂200 MW混流式水轮机为研究对象，采用真机试验的方法研究了尾水管压力脉动特性；文献[7]基于数值模拟方法分析了导叶开度变化对尾水管涡带形状及压力脉动特征的影响；文献[8]提出在尾水管直锥段设置鳍片抑制混流式水轮机部分负荷工况下压力脉动的方法。还有很多学者对水轮机内部压力脉动特性进行了相关研究[9-14]。然而，大部分研究是从内部流场机理方面解释压力脉动的成因，或从压力脉动信号本身的特征出发建立特征库，以便用于故障诊断，而关于建立一种辅助判定水轮机稳定性的技术方法的研究很少。在建立水轮机转轮水力模型的过程中经常需要对比同一部位测点的压力脉动特性，但仅以压力脉动信号幅值作为依据进行比较时会出现幅值相等或者极其接近的情况，这就需要另外一种辅助判定准则，对水轮机的稳定性进行判断。因此，需要从压力脉动信号数据中进一步提取信息，以辅助水轮机稳定性的判断。

本文提出一种基于压力脉动信号样本熵变化规律判定水轮机稳定性的方法。采用互补集合经验模态分解(Complete ensemble empirical mode decomposition, CEEMD)方法对压力脉动信号进行分解，在获得压力脉动信号数据的主分量后对主分量进行样本熵计算。然后结合水轮机内部流场观测和压力脉动幅值数据，验证基于压力脉动信号主分量样本熵变化规律分析水轮机内部流动状态的可靠性。

1 试验装置及测点布置

1.1 试验装置

混流式水轮机压力脉动数据均为实测数据。以“一带一路”沿线老挝某高水头水电站项目的模型水轮机为对象开展压力脉动测试试验，试验在浙江富安水力机械研究所满足IEC60193测试要求的高精度水力试验台上完成。模型水轮机的相关参数如表1所示。

表1 模型水轮机参数

水力机械试验台上安装的模型水轮机整体试验装置及模型水轮机转轮的实物图如图1所示。其中，模型水轮机的尾水管锥管段采用透明有机玻璃加工，方便观测尾水管内部流态。

1.2 压力脉动测点布置

采用多通道高精度压力脉动采集系统获取水轮机各部位的压力脉动，在模型水轮机的活动导叶与转轮间的无叶区、尾水管锥管以及尾水管肘管上均布置了2个压力脉动测点，测点布置的位置如图2(图中D2表示转轮出口直径，数字为测点序号)所示。

所有测点的压力脉动数据在试验过程中实现同步采集，这样可确保准确全面地反映水轮机运行中的整体稳定性，压力脉动传感器采用美国PCB公司生产的M112A型高频压力脉动传感器，采集所得的数据经过采集卡传输至计算机。在本文中，水轮机压力脉动测试数据和稳定性分析只针对3个部分负荷开度下共15组工况开展，工况的具体参数如表2所示。

表2中，每个活动导叶开度下均包含5个工况，分别对应不同的真机运行水头，其中水头262 m代表真机的最小运行水头，水头340 m代表真机的最高运行水头，额定水头为300 m。表2中的15个工况均为部分负荷工况，所有工况对应的负荷均小于85%额定负荷。

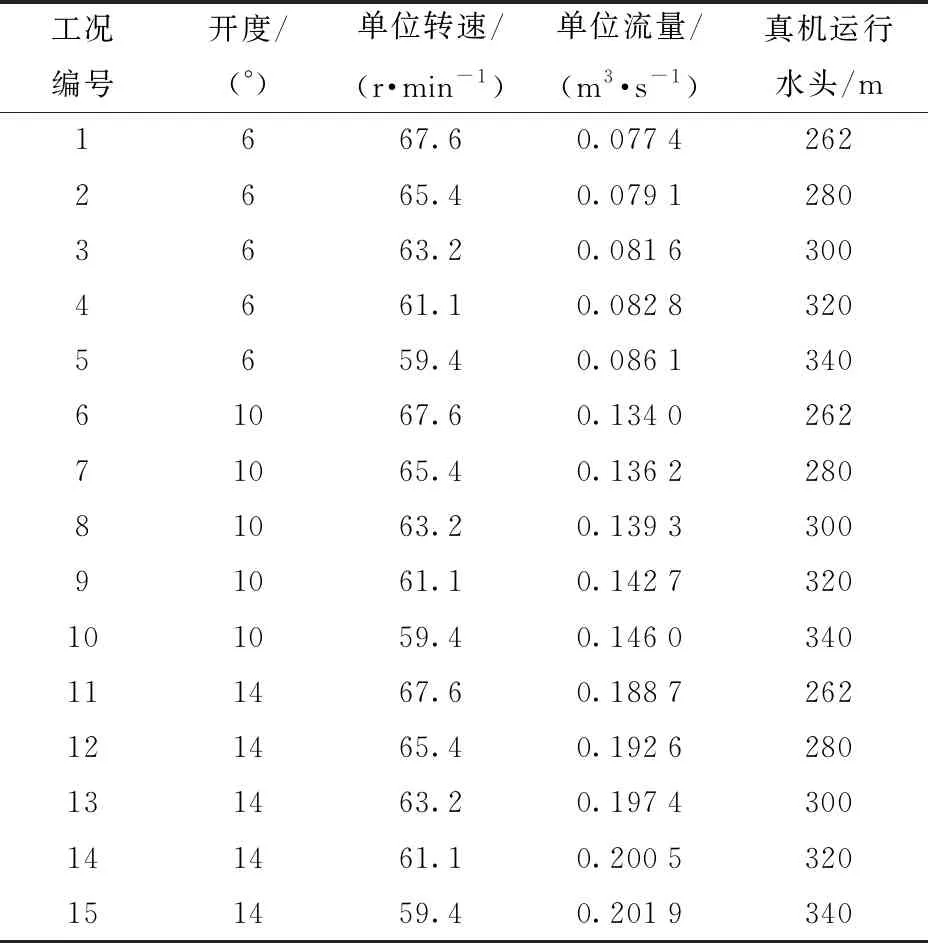
表2 测试工况参数

2 压力脉动数据的分析理论

2.1 CEEMD计算流程

高水头混流式水轮机各测点的压力脉动信号本质是非平稳时间序列，快速傅里叶变换是最常用的分析处理方法[15]。除此之外还有小波变换[16]、希尔伯特-黄变换[17]、经验模态分解(Empirical mode decomposition, EMD)[18-20]等近年来使用较多的分析方法。其中，EMD相比于小波变换的优势在于避免了量化误差的引入以及小波基函数的主观选取，但是仍存在模态混叠的缺陷。

综合比较上述方法，本文采用CEEMD[21-22]对压力脉动信号进行处理。CEEMD算法是通过加入互补的噪声来协助完成EMD的信号分解。由于加入的是互补的、独立并相同分布的噪声，两者完全负相关，所以在两组分解信号重构的时候可以最大限度地消除冗余噪声，这也是该算法的最显著优点。具体的算法流程如图3所示。

2.2 信号主分量选取方法及样本熵计算

将测试所得的压力脉动信号采用CEEMD算法进行分解以后会获得多个对应不同瞬时频率的固有模态分量(Intrinsic mode function, IMF)，从这些IMF分量中筛选出主要分量时须有统一的评判标准。采用互相关系数来完成IMF主要分量的选取。假如存在两组相同时间尺度的时间序列信号x(t)和y(t)，则这两组时间序列信号的互相关系数Rxy的计算公式为

(1)

(2)

(3)

x(i)、y(i)——两个时间序列信号中的采样数据

m——时间序列信号中的不同时间尺度

N——时间序列信号在整个采样时间的数据点数

计算获得的互相关系数Rxy均在0～1的范围内，数值越高代表两个时间序列的相关性越强。在筛选获得主要IMF分量以后，对其进行样本熵计算。样本熵是一种定量衡量非平稳时间序列复杂程度的数值，可以用于衡量经过提取后的水轮机压力脉动信号主分量的复杂性。因此当两个压力脉动信号的峰峰值相等或者极其接近时，压力脉动信号主分量的样本熵可用于辅助评判水轮机的稳定性。样本熵ES[23-24]的最终理论计算公式为

(4)

式中k——模式维数r——相似容限

但由于信号数据的长度N(即采样点数)都是有限值，所以ES的实际计算公式为

(5)

k和r都是预先确定的常系数，k取2.0，r则通常取(0.1～0.25)RStd，RStd为CEEMD分解前原始信号的标准差。Ak(r)和Bk(r)的含义在文献[25]中有详细介绍，在此不再赘述。

3 试验与结果分析

3.1 压力脉动信号数据的分析流程

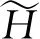
由于试验工况有15个，每个工况下有3个压力脉动测点数据，所以总的压力脉动信号数据有45组。45组压力脉动信号数据分解后分量多达405个，为了节约篇幅，本文只以工况2下测点1的信号数据为例，说明单个压力脉动信号数据进行CEEMD分解和样本熵计算的流程。工况2(开度为6°，单位转速为65.4 r/min，单位流量为0.079 1 m3/s)下的测点1(顶盖上游)采集得到的时域压力脉动数据如图4所示。

根据水轮机行业的试验测试标准，表征测点压力脉动振幅的无量纲特征幅值HAmp的计算公式为

(6)

式中 ΔH——压力脉动时域数据在97%置信区间内的峰峰值，m

H——模型试验时的水轮机工作水头，m

由于高水头混流式水轮机模型试验测试时的工作水头固定为30m，所以根据式(6)可计算得到图4所示测试信号的压力脉动振幅HAmp为3.052%。将该测点的压力脉动信号进行CEEMD分解，可得到如图5所示的IMF分量图。

获得各IMF分量以后，采用第2节提及的互相关分析方法计算各IMF分量与原始信号的互相关系数Rxy，并选取Rxy最高的IMF分量作为主要IMF分量。例如，在图5中，Rxy最高的分量为IMF5，因此选择IMF5作为工况2下测点1的压力脉动信号主分量，并对其进行样本熵的计算，最终计算得到IMF5的样本熵为0.036 3。上述对单个压力脉动信号数据的分析过程全部采用程序实现，如此可循环对各工况下不同测点的压力脉动信号进行处理，处理后可获得对应的压力脉动信号主分量，但每个压力脉动信号的IMF主分量序号不一定相同。

3.2 试验结果分析

因为本文只选取了测点1、3和5作为分析对象，所以下文只针对这3个测点的压力脉动信号数据进行分析。采用3.1节的方法对3个测点在不同工况下的压力脉动信号数据进行处理，获得每个压力脉动信号数据对应的IMF主分量。随后对这些主分量波形进行快速傅里叶变换，并统计出不同开度下主分量的主频随真机运行水头的变化规律，如图6所示。图6中，所有主频均按其与转频的比值f/fn表示。

从图6中可以看出，在极小开度6°时，3个测点处各工况下压力脉动信号主分量的主频均相同，均位于0.34～0.37倍转频之间，属于低频。在开度为10°和14°时，各工况下压力脉动信号主分量的主频开始出现差异，但主频数值仍低于0.6倍转频，所以仍属于低频成分。

在高水头混流式水轮机内部，诱发压力脉动的水力根源通常为动静干涉、卡门涡或尾水管空腔涡带。前两种水力根源诱发的压力脉动均为高频压力脉动，只有尾水管空腔涡带诱发的压力脉动为低频压力脉动，且主频在1倍转频以下。结合图6可知，在活动导叶开度为6°和10°下的所有工况，水轮机顶盖、尾水管锥管及肘管处的压力脉动主分量均为尾水管空腔涡带产生的低频压力脉动。在活动导叶开度为14°下，除工况12以外，其余工况下各测点的压力脉动主分量也均由尾水管内部的空腔涡带所诱发。在工况12时，顶盖处测点1的压力脉动主分量频率与尾水管内的两个测点均不一致，因此该工况下顶盖测点的压力脉动主分量可能由其它原因所引发。尾水管内部的流场观测结果也验证了该结论，限于篇幅，图7只给出了3个开度下对应额定水头时的尾水管内部流态，即工况3、8、13下的尾水管内部流态加以证明。

图7中尾水管内部空腔涡带的形状都采用白色虚线进行了描绘，从图7a和图7b中可以看出，在额定水头6°和10°这两个小开度工况下，尾水管内部均出现了明显的尾水管空腔涡带，且空腔涡带的形状粗壮，呈微螺旋型。实际观测中，该尾水管内部的空腔涡带一直作旋转摆动，并发出较大噪声，所以可判断出尾水管涡带是尾水管内部压力脉动的主要源头。同时，尾水管内部明显的压力脉动现象不仅影响下游肘管段的稳定性，还向上游传播影响到了上游顶盖处测点的压力脉动，所以在图6a和图6b中，3个测点的压力脉动主分量的主频都基本一致。当活动导叶开度增大到14°以后，尾水管内部空腔涡带的尺度明显缩减，从图7c中可以看出大尺度空腔涡带已明显缩小为只在转轮泄水锥附近摆动的双螺旋小涡带，由此导致了图6c中开度14°下压力脉动主分量的主频出现差异。

3.3 压力脉动的样本熵计算分析

为了分析不同工况下压力脉动信号的特征，本文将CEEMD分解后得到的所有压力脉动信号的主分量进行了样本熵计算，并对3个测点下的压力脉动信号主分量的样本熵变化规律进行了三次曲面拟合，结果如图8d～8f所示。在图8a～8c中则给出了常规稳定性评价所需计算的3个测点下的压力脉动幅值HAmp。

按常规水轮机稳定性分析方法，综合测点的压力脉动信号幅频特性以及内部流态试验图像可以判定混流式水轮机内部的流动状态是否为非稳定流动，并据此推断水力不稳定源的类型。因此，综合本文图6、7以及图8a～8c中的结果可知，活动导叶开度为6°(极小开度)时，水轮机内部存在尾水管空腔涡带不稳定流动现象并造成幅值较高的压力脉动，表明水轮机内部流动处于不稳定状态，但随着导叶开度增大到10°和14°时，这种不稳定现象逐渐减弱，水轮机的运行状态向稳定状态发展，压力脉动的幅值也回落至较小值。最终，水轮机的稳定性变化方向如图8a～8c中白色箭头所示。上述试验结果表明，部分负荷工况下尾水管空腔涡带是影响高水头混流式水轮机稳定性的根源之一。

图8d～8f展示了压力脉动信号主分量的样本熵在整个测试范围内的分布规律。结合图8d～8f的结果与前述分析得到的水轮机稳定性变化方向可知，当水轮机运行在相对不稳定状态下时(活动导叶开度为6°)，3个测点处压力脉动信号主分量的样本熵均较高。随着活动导叶开度逐渐增加，水轮机运行状态趋于稳定后，压力脉动信号主分量的样本熵与压力脉动幅值一样呈现出明显的下降规律。由此可见，测点处压力脉动信号主分量的样本熵随机组运行状态的变化规律与压力脉动幅值HAmp相似，可以在一定程度上反映水轮机内部流动状态的变化趋势。因此，压力脉动信号主分量的样本熵分析可作为一种研究水轮机内流状态变化趋势的技术方法。

4 结论

(1)在部分负荷工况下，增加活动导叶开度可以显著减小尾水管空腔涡带的尺度，进而降低水轮机各部位压力脉动的振幅。这也证明，部分负荷工况下尾水管空腔涡带是影响高水头混流式水轮机稳定性的主要因素。

(2)综合水轮机模型试验流态观测和各测点处压力脉动信号主分量的频谱分析结果可以发现，水轮机各部位处压力脉动信号主分量的频率信息可准确地反映水轮机内部是否存在水力不稳定源，因此可据此推断水力不稳定源的类型。

(3)各测点处压力脉动信号主分量的样本熵在高水头混流式水轮机运行范围内的变化趋势可以反映水轮机内部流动状态的变化趋势，因此，压力脉动信号主分量样本熵分析可作为研究水轮机内流状态变化趋势的技术方法。