变压器振动在典型建筑结构中的衰减特性*

卢 铃 谢紫银 吴晓文 Hakbong Kim 李 军 翟国庆

(1 国网湖南省电力有限公司电力科学研究院(国网电力设施噪声与振动实验室)长沙 410007)

(2 浙江大学环境过程研究所 杭州 310058)

0 引言

随着城市化的快速推进和居民用电负荷的不断增长，居民区配电变压器数量持续增加。位于建筑物内的变压器在运行过程中，其振动可通过建筑结构传播，产生室内二次结构噪声污染[1-4]。当建筑物局部结构固有频率与变压器振动频率接近时，室内二次结构噪声尤为突出[5]。为控制变压器振动引起的室内二次结构噪声污染，有必要研究掌握居民区10 kV配电变压器振动在不同类型建筑结构中的衰减特性。

本文采用有限元法建立两种典型建筑(剪力墙结构和框架结构)的三维有限元模型，通过仿真研究变压器振动在典型建筑结构中的衰减特性。

1 典型建筑结构模型

分别建立典型多层(8 层)、高层(20 层)[6]框架、剪力墙结构建筑模型，其中地下室均为2 层，建筑层高均为3 m，负一层楼板厚度均取200 mm，其余楼层楼板厚均为120 mm。框架建筑柱间距4.5 m，柱截面800 mm×800 mm，梁截面300 mm×600 mm；剪力墙建筑墙厚200 mm。主要建筑材料为混凝土C40，根据《混凝土结构设计规范》[7]，混凝土C40的泊松比、密度和杨氏模量分别为0.2、2500 kg/m3和32.5 GPa。建筑结构底部设为固定支座，并约束X、Y、Z方向的平移和转动。图1为多层建筑三维有限元模型结构示意图。

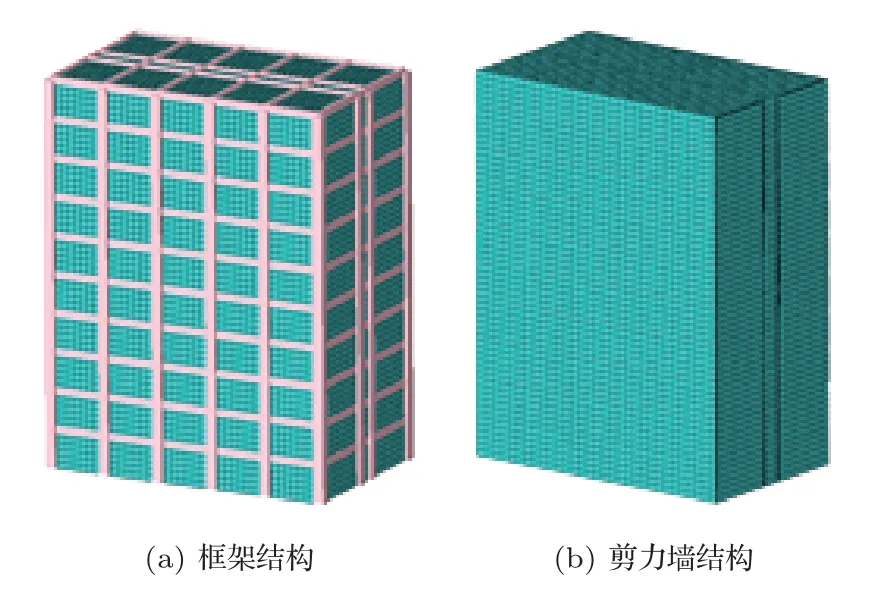
图1 典型多层建筑结构有限元模型Fig.1 Finite element models of typical multistory building structures

2 仿真方法及参数设置

模型单元的选择是进行建筑结构动力响应分析的关键，相比于固体单元，三维梁单元和板单元可以在保证计算精度的前提下大幅降低计算量。因此，梁和柱采用两节点空间线性梁单元进行仿真，楼板采用四节点曲面薄壳或厚壳单元进行仿真。

2.1 阻尼参数

变压器振动以弹性波的形式在建筑结构中传播，结构阻尼通常采用瑞利阻尼C进行分析，其表达式为

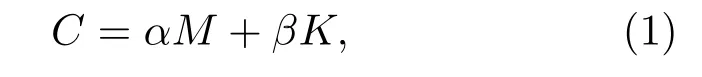
其中，M为质量阻尼，K为刚度阻尼；α和β是常数，分别是质量阻尼系数和刚度阻尼系数，通过式(2)、式(3)获得：

其中，ξ是材料的阻尼比，钢筋混凝土的阻尼比一般为0.02～0.05[7]；ω1、ωn分别取结构第一阶振型频率和变压器的关心振动频率对应的角频率[8]。

2.2 网格尺寸

为保证计算结果的准确度，有限元模型网格单元最大尺寸应小于最小关心波长的1/6～1/12。本研究中选取所关心振动频段(0～500 Hz)最小波长的1/12 为网格最大单元尺寸，即最大单元尺寸取500 Hz对应波长的1/12。

2.3 激励力及加载方法

为获取变压器振动通过4 只底脚传递至地面的激励力，现场采样某住宅区10 kV 干式变压器4只底脚铅垂向振动加速度时程数据，采样频率为1000 Hz，取时长为2 s 的数据。所选取的变压器总质量为2000 kg，不妨设变压器4 只底脚所受静载荷基本相同，则按牛顿第二定律可计算得到通过变压器每只底角传递至楼板的竖向激励力。通过4 点激励将变压器通过底脚传递给地面的力作用于建筑负一层中央。图2、图3分别为变压器一底脚处铅垂向振动加速度时程数据及其频谱图。

图2 变压器一底脚处铅垂向振动加速度时程数据Fig.2 Data of vertical vibration acceleration in time domain in at a foot of transformer

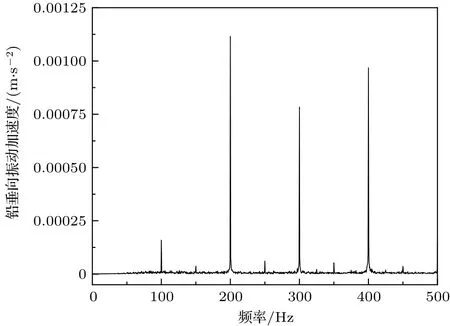
图3 变压器一底脚处铅垂向振动加速度频谱图Fig.3 Spectra of vertical vibration acceleration at a foot of transformer

3 结果与分析

3.1 振动衰减特性

以建筑负一层中央点为参考点，计算各楼层中央点0～500 Hz 铅垂向振动加速度级(Vibration acceleration level，VAL)相对于参考点的衰减量，其中参考点处振动加速度级取变压器4 只底脚处振动加速度级的算术平均值。对不同楼层的振动加速度级衰减量进行线性拟合，其中横坐标为所在楼层离地高度h的对数值，纵坐标为铅垂向振动加速度级衰减量，拟合函数的决定系数(R2)均高于0.9，结果见图4。由图4可知，变压器振动随楼层增加而不断衰减。在具有相同层高、层数的剪力墙、框架结构高层建筑中，位于负一层的变压器传播至各楼层的振动加速度级(0～500 Hz)随楼层离地高度h对数值(lgh)的增加线性下降，其斜率分别为33.26 和24.84，可见前者的衰减速率(lgh每增加1 振动加速度级的衰减量)约为后者的1.3倍；在剪力墙、框架多层建筑中斜率分别为31.87 和20.07，前者约为后者的1.6 倍。可见，当建筑层高、层数相同时，变压器铅垂向振动加速度级在剪力墙结构中比框架结构中衰减更快；当建筑结构相同时，振动加速度级在高层建筑中的衰减速率略大于多层建筑。

图4 不同结构类型建筑中0～500 Hz 铅垂向振动加速度级衰减量Fig.4 Attenuation values of 0～500 Hz vertical vibration acceleration level in the buildings of different structure types

由图5可知，变压器引起的各楼层环境振动(0～80 Hz)铅垂向Z振级(VLZ)相对于参考点的衰减值同样与所在楼层离地高度h的对数值线性相关。在剪力墙结构和框架结构的高层建筑中，变压器传播至各楼层的铅垂向Z 振级随楼层离地高度h对数值(lgh)的增加线性下降，其斜率分别为29.27和12.23，前者约为后者的2.4 倍；在剪力墙结构和框架结构的多层建筑中斜率分别为39.96 和10.83，前者约为后者的3.7 倍。可见，对0～80 Hz 的环境振动，变压器铅垂向Z 振级在剪力墙结构建筑中的衰减速率同样大于框架结构建筑。

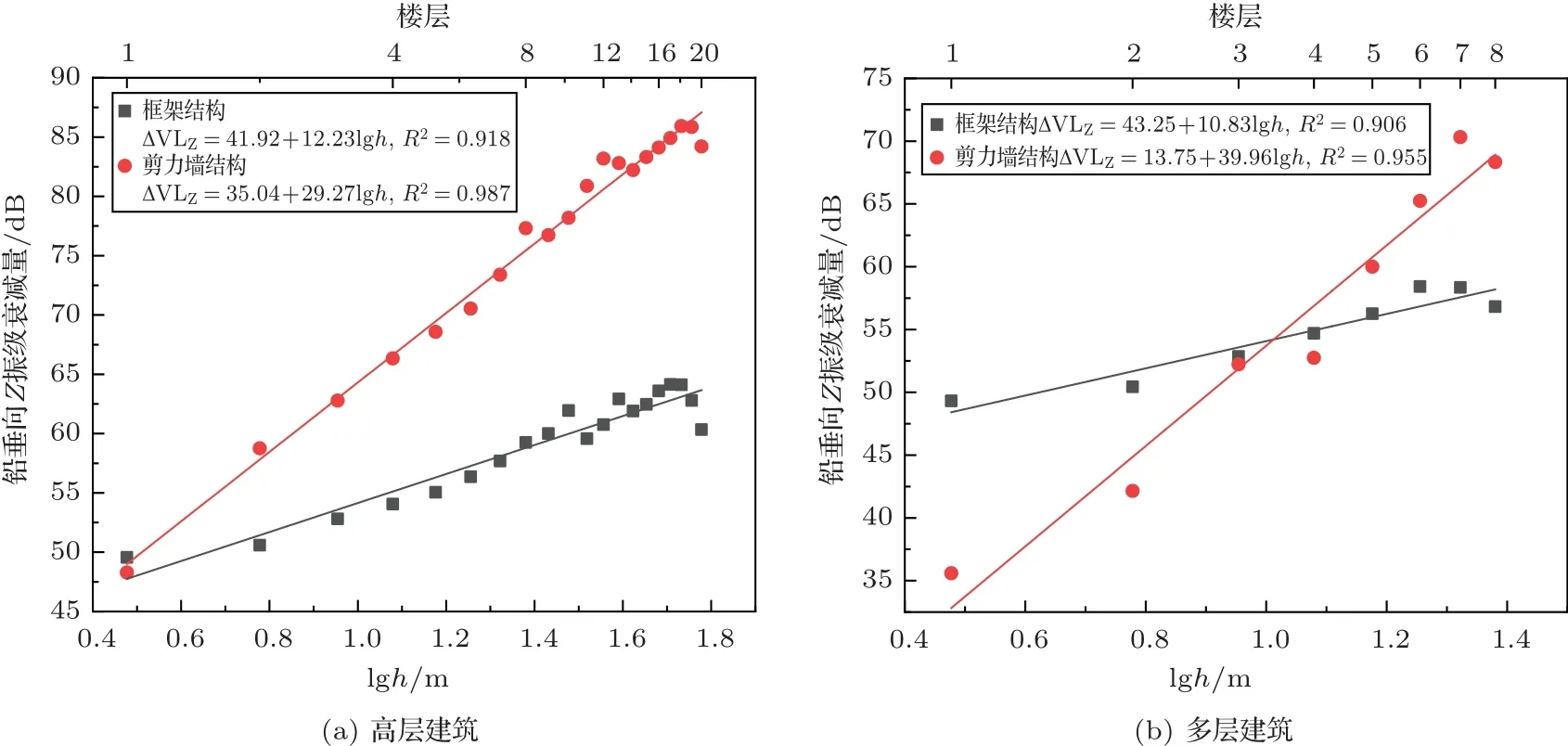
图5 不同结构类型建筑中0～80 Hz 铅垂向Z 振级衰减量Fig.5 Attenuation values of 0～80 Hz vertical Z-weighted vibration level in the buildings of different structure types

3.2 振动响应频谱

图6为框架和剪力墙结构多层建筑不同楼层0～500 Hz 铅垂向振动加速度级1/3 倍频程谱。由图6可知，当建筑层数均为8 层时，框架结构建筑不同楼层铅垂向振动加速度级在50～100 Hz、200 Hz及300 Hz 处出现峰值，剪力墙结构在100 Hz、200 Hz 及300～400 Hz 处出现峰值。与本仿真结果相似，洪陈玉[8]对变压器引起建筑梁、柱、板等结构振动进行实测，结果表明振动主要集中在100 Hz及其谐频处。

图6 不同结构类型建筑0～500 Hz 振动加速度级1/3 倍频程谱Fig.6 1/3 octave spectrum of 0～500 Hz vibration level in the buildings of different structure types

3.3 框架和剪力墙建筑不同楼层振动单值预测模型

根据仿真结果，通过引入建筑各楼层中央点处的铅垂向振动衰减量，建立了变压器传播至建筑各楼层的振动单值预测模型，该模型可预测具有剪力墙结构、框架结构的高层、多层建筑各楼层中央点处的振动加速度级和Z振级。

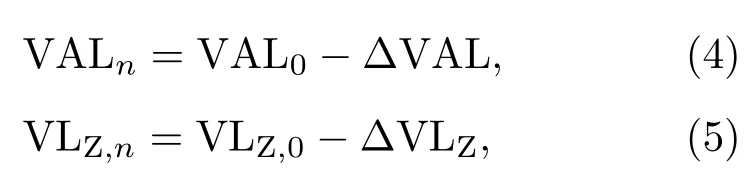
其中，

其中，VALn、VLZ，n分别为建筑第n层楼板中央点处铅垂向振动加速度级(dB)、Z 振级(dB)；VAL0、VLZ，0分别为变压器所在楼层(建筑负一层)中央点处振动加速度级(取变压器4 只底脚处振动加速度级的算术平均值)(dB)、Z振级(dB)；ΔVAL、ΔVLZ分别为铅垂向振动加速度级衰减量(dB)、Z 振级衰减量(dB)；h为各楼层离地高度(m)；n为楼层数；Δh为楼层层高(m)。

3.4 框架和剪力墙建筑不同楼层振动分频段预测模型

前面所建立的单值振动预测模型与振动源的频谱(即变压器底脚处的振动加速度频谱)相关，为提高预测精度，可进一步对振动影响进行分频段预测。

根据仿真得到的各楼层中央点处的振动响应值1/3 倍频程谱，可计算得到各楼层相对于变压器所在楼层在第i个1/3 倍频程上的铅垂向振动加速度级衰减量ΔVALi，结果见图7和图8，经Z计权后可进一步得到各楼层中央点处第i个1/3 倍频程上铅垂向Z振级衰减量ΔVLZ，i。

图7 多层建筑各楼层中央点1/3 倍频程中心频率处铅垂向振动加速度级衰减量Fig.7 The attenuation of vertical vibration acceleration level at the center frequency of 1/3 octave at the center point of each floor in multi-story buildings

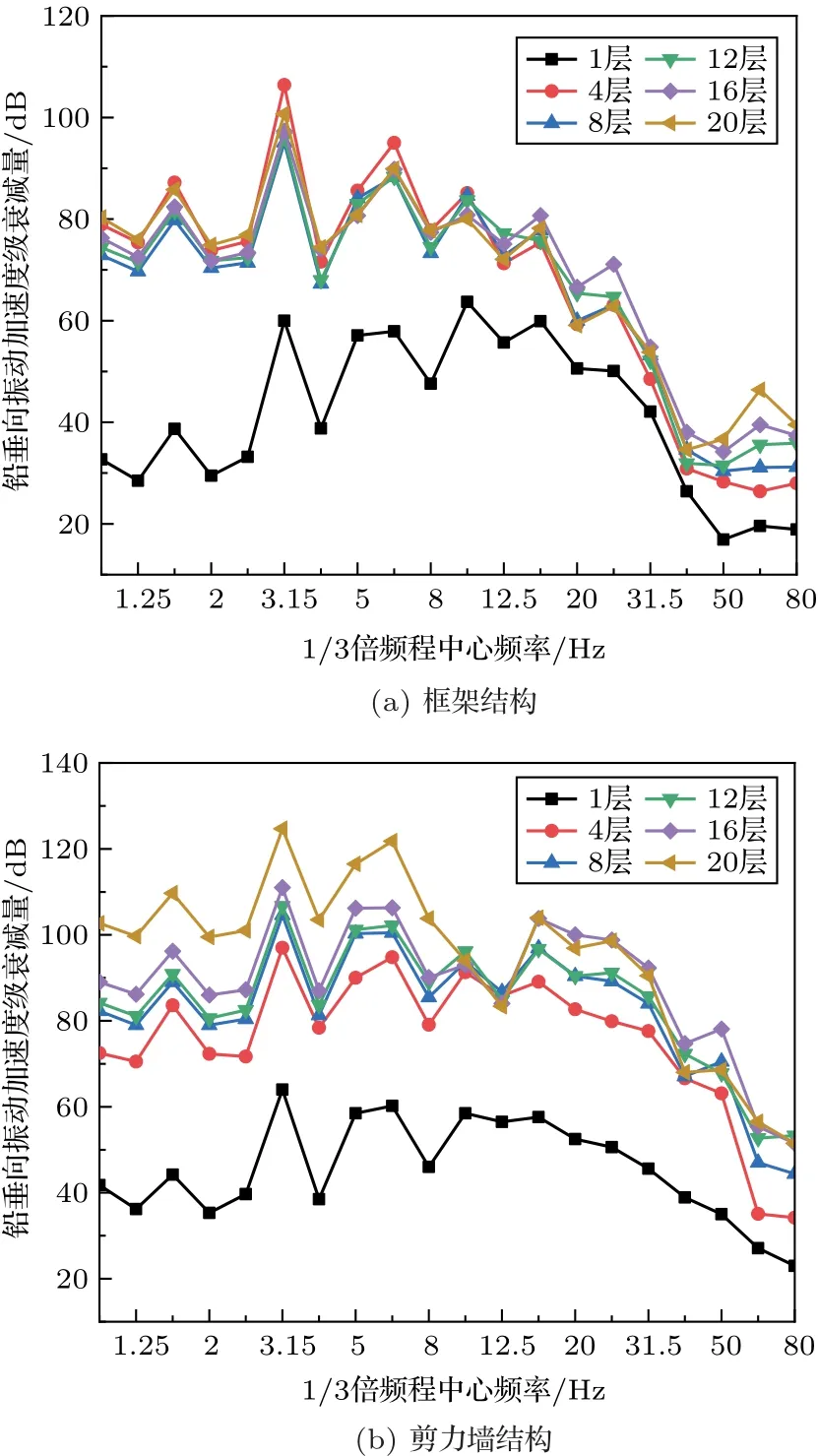
图8 高层建筑典型楼层中央点1/3 倍频程中心频率处铅垂向振动加速度级衰减量Fig.8 The attenuation of vertical vibration acceleration level at the center frequency of 1/3 octave at the center point of typical floors in high-rise buildings

利用图7和图8的ΔVALi，根据式(9)可得到不同楼层第i个1/3 倍频程上的铅垂向Z 振级VLZ，i。

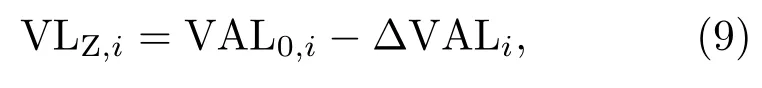
式(9)中，VLZ，i为某楼层中央点处第i个1/3 倍频程铅垂向Z振级(dB)；VAL0，i为变压器所在楼层中央点处第i个1/3倍频程铅垂向振动加速度级(dB)；ΔVALi为第i个1/3倍频程铅垂向振动加速度级衰减量(dB)。

由图7和图8可知，在0～80 Hz频段内，框架结构在0～30 Hz 低频段内振动加速度级衰减较为明显，而剪力墙结构在0～50 Hz中低频段内振动衰减较为明显。

4 结论

利用实测变压器振动加速度数据，通过仿真研究了变压器振动在不同建筑结构中的衰减特性。结果表明，在具有相同层高、层数的剪力墙、框架高层建筑中，位于负一层的变压器传播至各楼层的振动加速度级(关心频段0～500 Hz)随楼层离地高度h对数值(lgh)的增加线性下降，前者的衰减速率约为后者的1.3 倍；在剪力墙、框架多层建筑中，前者的衰减速率约为后者的1.6倍。对0～80 Hz 的环境振动，在剪力墙结构和框架结构的高层建筑中，变压器传播至各楼层的铅垂向Z振级也随楼层离地高度h对数值(lgh)的增加线性下降，前者的衰减速率约为后者的2.4 倍；在剪力墙结构和框架结构的多层建筑中，前者的衰减速率约为后者的3.7倍。在此基础上，建立了变压器传播至剪力墙、框架建筑不同楼层处的振动单值和分频段预测模型，可为变压器引起的建筑室内振动预测和控制提供依据。