声子晶体结构在功率超声换能器中的应用*

胡理情 林书玉

(陕西师范大学 陕西省超声学重点实验室 西安 710119)

0 引言

夹心式压电陶瓷换能器，又称为朗之万换能器，由于其具有结构简单、能够在较低共振频率下获得纵向振动等优点，在大功率超声和水声领域应用较为广泛[1]。一般情况下，换能器的振动模式实际是纵向振动与横向振动的相互耦合，换能器的横向尺寸应小于其对应特征频率在陶瓷材料中声波波长的四分之一，以保证换能器使用一维振动产生的误差可以忽略不计，此时可以忽略横向振动。但是随着换能器的应用范围的扩大，有两种情况不可忽略换能器的横向振动：第一种是当换能器在高频工作时，相应波长减小，横向尺寸也需要减小，但是会造成换能器的机械强度下降，为了使换能器工作在高频，必须增大横向尺寸，此时尺寸就会大于波长的四分之一，此时换能器的横向振动不可忽略；第二种是在例如超声焊接等功率超声的应用中，需要大功率的超声，此时需要增大换能器的横向尺寸[2]。在这两种情况下，必须对换能器进行优化来抑制耦合振动对换能器的影响。林书玉等[3]、梁召峰等[4]通过焊接头开槽来改进超声焊接系统，基本上解决了换能器的耦合振动问题，但是并没有用理论来解释开槽如何对振动进行影响。随着声子晶体结构带隙理论的出现，越来越多的学者将其应用于减振降噪方面，而这种周期性的开槽结构就类似于声子晶体的周期型结构排列。由声子晶体的定义可知，它是由密度和弹性常数不同的两种材料按周期性结构复合在一起形成，图1(a)是一个二维声子晶体结构，互不连通的材料称为散射体，连通为一体的材料称为基体[5]，图1(b)为声子晶体原胞的截面图，其中圆形为散射体，其余为基体，a为原胞的晶格常数，r为散射体的半径。声子晶体结构形成的特殊色散关系，会使得处于带隙范围内的弹性波被禁止传播。将开槽后的结构定义为一个声子晶体结构，空气为散射体，剩余材料为基体，由此可以解释对横向振动的抑制作用是由于共振频率处于声子晶体带隙范围内，被禁止传播。由图1(a)可以看出，二维声子晶体结构与1-3型复合材料结构相似，Wilm等[6]将1-3 型复合材料对横向振动的抑制作用从声子晶体理论角度进行解释，采用平面波展开法，在考虑了压电效应、声损失和电激励条件下，得到了色散关系；为了将材料应用于超声成像，Wilm 等[7]得到了非零的角度入射时的带隙图；Aragón 等[8]和Ronda等[9]也研究了带有压电效应的声子晶体，在压电陶瓷片的厚度方向周期性地开圆形孔阵列来抑制横向振动，说明有限周期的圆柱形孔的声子晶体在对耦合振动的抑制有明显的效果。但是由于压电陶瓷片脆性大，对其开孔难度较大，本文选择在前盖板上开周期结构圆柱形孔。换能器的前盖板作用是为了将换能器产生的能量沿着纵向高效地辐射出去，辐射面位移分布越均匀，辐射阻抗越大，能够有效提高换能器的辐射功率，将前盖板设计成声子晶体结构，调整尺寸使共振频率处于带隙内，从而达到抑制横向振动的目的。Khelif 等[10]研究了在声子晶体中声波的传播问题，除散射体的填充率外，完全带隙是否存在以及带隙的宽度与声子晶体的厚度与晶格周期的比值也有关系；王莎等[11]在喇叭形前盖板上沿半径方向开周期性槽，调整开槽高度和宽度来达到抑制横向振动的目的，这是一种类声子晶体结构模型，可以得知散射体的高度和大小对声子晶体的带隙特性存在很大的影响。

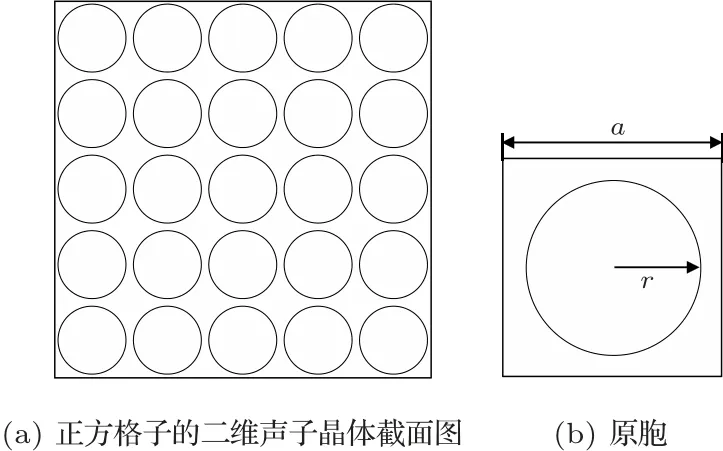
图1 二维声子晶体及原胞截面图Fig.1 Cross section of two-dimensional phononic crystal and primitive cell

色散曲线图能够直观地了解声子晶体的带隙特性，平面波展开法是求解声子晶体色散曲线最常用的方法之一。理想的二维声子晶体在两个维度是无限周期的，不考虑厚度的影响，采用平面波展开法可以计算出它的能带结构，但是功率超声换能器的结构是有限大小的，基于声子晶体结构的前盖板只能是有限周期结构，要使得声子晶体应用于功率超声换能器中，需要计算出有限周期结构的声子晶体的传输特性[12]。本文采用有限元法仿真了二维声子晶体前盖板的传输特性，将共振频率设计在带隙范围内，通过对不同高度和半径的散射体带隙进行计算并结合共振频率分析，找到前盖板的最佳尺寸，使其最大程度地对横向振动进行抑制，明显降低径向振动位移，辐射面位移分布也更加均匀。

1 基于二维声子晶体结构的前盖板对换能器共振频率的影响

传统的夹心式换能器由等截面的圆柱形前后盖板和压电陶瓷片组成，陶瓷片的极化沿厚度方向，如图2(a)所示的传统的夹心式换能器，中间是由两块陶瓷片组成，极化方向相反，整个振子的厚度等于基波的半波长，横向尺寸远小于纵向长度，满足一维振动理论。但是受实际应用的影响，换能器的横向尺寸相对较大时，产生强烈的耦合振动会导致换能器的效率下降，因此，本文设计了一种具有基于二维声子晶体结构前盖板的功率超声换能器，模型如图2(b)所示，换能器的共振频率在20 kHz 附近，前后盖板高度为56 mm，整体的截面半径R为26 mm，压电陶瓷片的厚度为6 mm，在前盖板的前端沿纵向开圆柱形孔，形成近周期构开孔结构，即声子晶体结构。前盖板开孔后的截面如图2(c)所示，黑色正方形为声子晶体的一个原胞，在x和y方向为近周期性结构，晶格常数a为10 mm，散射体半径为r。

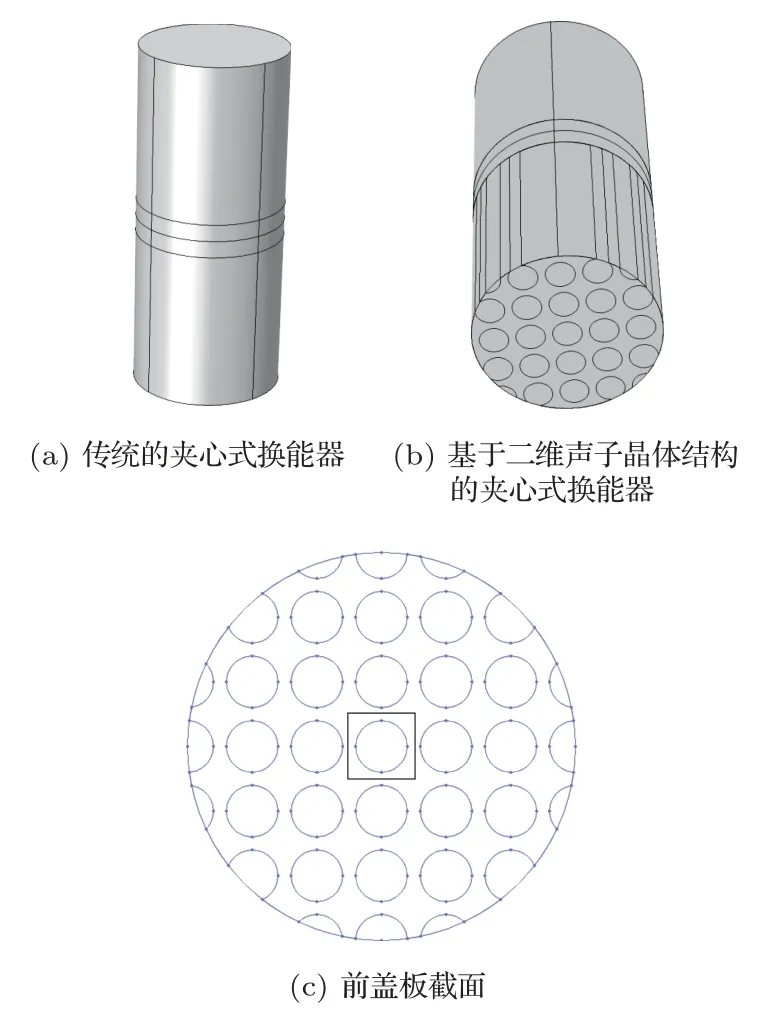
图2 传统的夹心式换能器模型和基于二维声子晶体结构的夹心式换能器模型Fig.2 Traditional sandwich transducer model and sandwiched transducer based on two-dimensional phononic crystal structure model

通过有限元法研究散射体的大小对换能器的纵向共振频率的影响，在静电场和固体力学两个物理场中进行研究，建立换能器的几何模型如图2所示，前盖板和后盖板的材料定义为铝，两个压电陶瓷片的材料为PZT-4，为了简化模型，本文暂不考虑预应力螺栓对换能器振动特性的影响。通过对特征频率求解得出模型的纵向共振频率，图3(a)是仿真得到的传统夹心式换能器的振型图，可知不开孔时换能器的纵向共振频率为19.871 kHz。将模型前盖板改为声子晶体结构，基体为铝，散射体是空气，图3(b)是散射体半径为4 mm 时换能器的振型图，得到的纵向共振频率为20.396 kHz，可知散射体的半径对换能器的共振频率存在影响。本文进一步通过改变散射体的半径或者高度对换能器的特征频率进行研究。

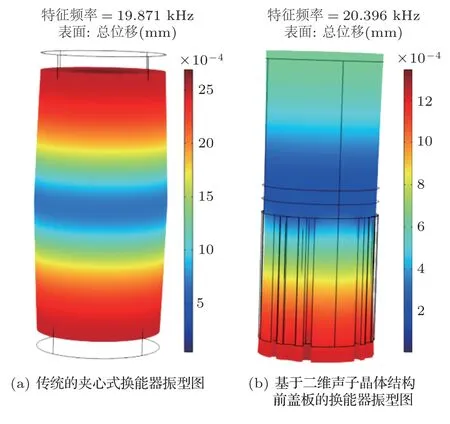
图3 传统的夹心式换能器和基于二维声子晶体结构前盖板的换能器的振型图Fig.3 The vibration pattern diagram of traditional sandwich transducer and the transducer based on the front cover plate with twodimensional phonon crystal structure

保持其他结构参数不变，改变声子晶体结构前盖板的散射体半径。分别在有限元软件中建立散射体半径为3.7 mm、3.8 mm、3.9 mm、4.0 mm、4.1 mm、4.2 mm、4.3 mm、4.4 mm、4.5 mm 的换能器模型，对模型的特征频率进行研究，得到纵向共振频率分别为20.288 kHz、20.322 kHz、20.358 kHz、20.396 kHz、20.441 kHz、20.488 kHz、20.533 kHz、20.586 kHz、20.638 kHz，关系图如图4(a)所示，可知随着前盖板散射体半径的增大，换能器的纵向共振频率也在逐渐增加。同样的保持其他结构参数不变，将散射体半径固定为4 mm，通过改变散射体的高度来观察功能共振频率的变化，建立散射体高度分别为0 mm、7 mm、14 mm、21 mm、28 mm、35 mm、42 mm、49 mm、56 mm 的模型，纵向共振频率分别为19.871 kHz、18.502 kHz、17.861 kHz、17.468 kHz、17.324 kHz、17.525 kHz、18.060 kHz、19.021 kHz、20.396 kHz，关系图如图4(b)所示，可知随着前盖板散射体高度的增加，共振频率先减小后增大。研究表明，前盖板散射体的大小对换能器的振动特性影响存在规律性，换能器的共振频率可以通过散射体进行调节，结合声子晶体结构前盖板的带隙范围设计夹心式换能器，能找到声子晶体结构前盖板的最佳尺寸，使得横向振动得到最好的抑制。

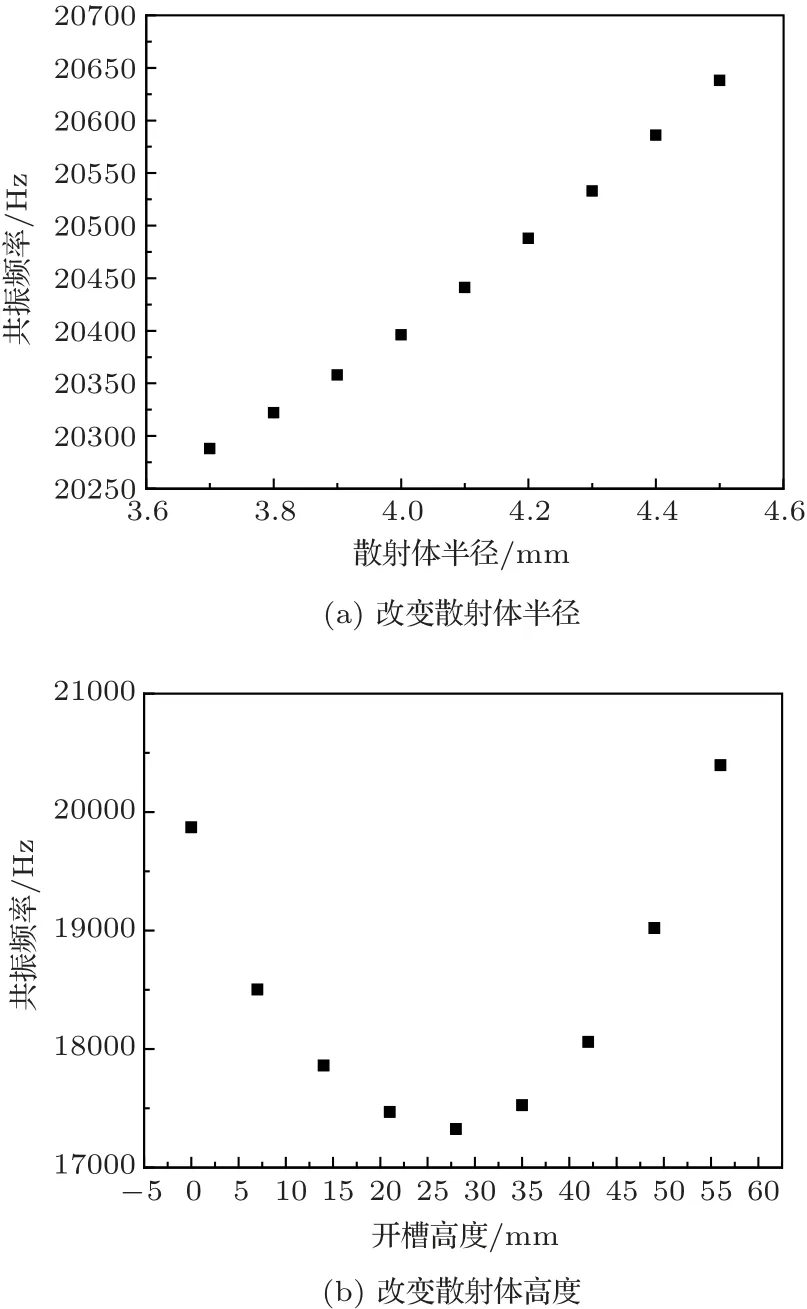
图4 夹心式换能器的共振频率Fig.4 Resonant frequency of sandwich transducers

2 二维声子晶体结构前盖板带隙的研究

2.1 散射体半径和高度对带隙的影响

近年来有不少学者对换能器耦合振动的抑制进行了研究，将超声塑料焊接系统的工具头开周期性结构的槽，有效实现了焊接系统的优化[13-14]，表明声子晶体的带隙特性对于横向振动的抑制确实存在很好的效果。对于纵向振动的夹心式换能器，也需避免与其他模式的振动耦合，造成换能器的效率低下。声子晶体结构对频率处于带隙范围内的振动才会具有抑制作用，可以确定二维声子晶体结构前盖板是否存在带隙以及依据存在带隙的范围来考虑是否对换能器的耦合振动存在抑制。声子晶体结构前盖板是有限周期结构，采用有限元仿真对其带隙进行研究。首先研究散射体的半径对声子晶体结构前盖板带隙的影响，在前盖板开周期性结构的孔，改变孔的半径大小。对于声子晶体结构的研究在有限元软件的固体力学模块中进行，将模型沿径向施加1 m/s2加速度幅值，使得弹性波在二维声子晶体结构前盖板中传播，在对应的另一侧进行计算，得出模型的加速度响应曲线，将加速度幅值小于1 m/s2时的频率范围定义为求解模型的带隙。带隙研究的模型为前盖板，高度为56 mm，改变散射体半径，分别建立散射体半径为3.8 mm、4.0 mm、4.2 mm、4.4 mm 的4 个模型；保持散射体半径为4 mm，改变散射体高度，分别建立散射体高度为56 mm、49 mm、42 mm、35 mm、28 mm的5个模型。对所建立的模型的频域进行研究得到的加速度响应曲线的结果，如图5所示。

从图5(a)可以看出，在换能器的设计共振频率20 kHz 附近不同散射体半径的散射体带隙存在情况不一样，并且散射体的半径对声子晶体前盖板的带隙存在很大的影响，由图中的4 个不同散射体半径时的加速度响应曲线可知，当散射体半径为3.8 mm 时，带隙范围是17.0～25.4 kHz；当散射体半径为4.0 mm 时，带隙范围是15.7～23.1 kHz；当散射体半径为4.2 mm 时，带隙范围是14.4～21.0 kHz；当散射体半径为4.4 mm 时，带隙范围是17.0～25.4 kHz。带隙范围的大小随着散射体半径的增大而减小，并且向高频方向移动。结合模型的共振频率进行分析，散射体半径为4 mm 时的共振频率对应的加速度幅值的衰减是最大的，此时的减振效果是最好的。再对散射体高度对带隙的影响进行分析，图5(b)是保持散射体半径为4 mm、改变散射体高度时，计算得到的加速度响应曲线，从图中可以看到随着散射体高度的增加，带隙向低频方向移动，而共振频率随着散射体高度先减后增，很明显可以得到散射体高度为56 mm 时的共振频率对应的加速度幅值的衰减是最大的。综合以上仿真所得到的结果进行分析，可以得知此换能器能够有效抑制横向振动时前盖板最佳尺寸是散射体半径为4 mm、高度为56 mm，此时共振频率处在带隙范围内并且加速度幅值的衰减强度接近最大值，对换能器的耦合振动抑制效果最好。

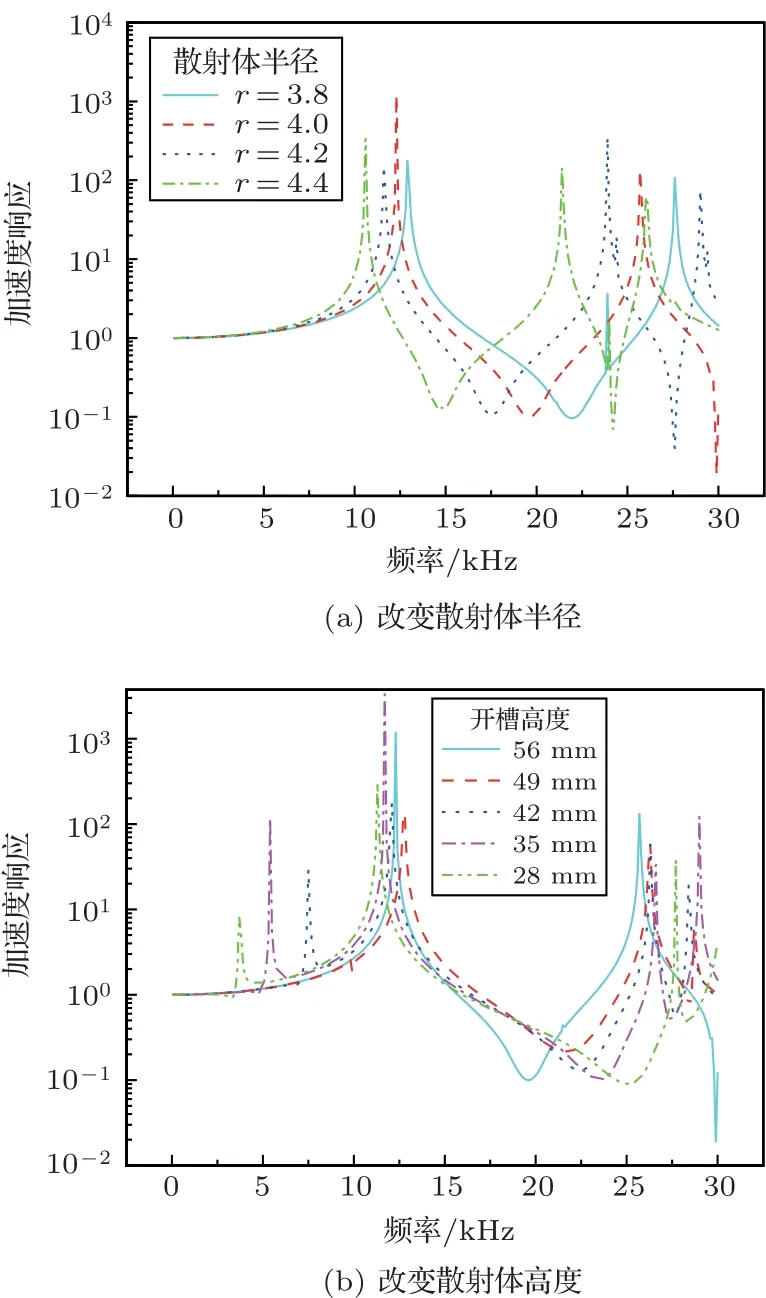
图5 加速度响应曲线Fig.5 Acceleration response curve

2.2 声子晶体结构前盖板对换能器振动特性的影响

利用有限元的方法基于声子晶体带隙理论对前盖板开孔结构的横向振动抑制作用进行了分析，得到了具有声子晶体结构前盖板的换能器的最佳设计尺寸，本文接着对径向位移进行计算，研究其对换能器横向振动的抑制效果。将换能器的振型图通过有限元仿真出后，对换能器前盖板侧面沿着正对着模型的y轴方向从上至下取截线距离为0～56 mm，如图6所示。定义取截线的方向为y方向，通过有限元分析计算得出换能器在径向的相对位移如图7所示，红色虚线为传统夹心式的径向位移，黑色实线为具有声子晶体结构前盖板的换能器的径向位移，径向位移在前盖板开周期性结构孔径后明显变小，表明声子晶体结构前盖板对换能器的横向振动存在明显抑制效果。本文还对换能器的前盖板辐射面的位移进行计算，研究换能器位移分布的均匀性。同样采取对前盖板前端的辐射面取截线对其纵向位移进行计算，前盖板未开孔时纵向振动最大位移与最小位移的之差为0.19 μm，采用声子晶体结构前盖板后纵向振动最大位移与最小位移的之差为减小为0.12 μm，说明此时换能器的位移分布更加均匀，辐射面的位移分布越均匀，辐射阻抗越大，从而辐射功率增大，提升了换能器的性能。

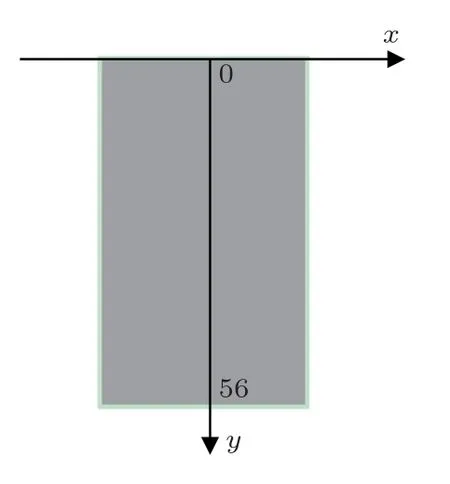
图6 前盖板侧向截线示意图Fig.6 Diagram of longitudinal transversal of front cover plate

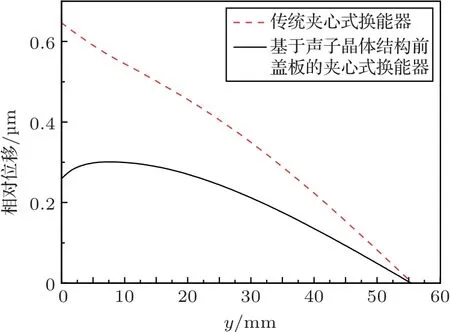
图7 换能器的径向位移Fig.7 The radial displacement of the transducer

3 结论

本文基于声子晶体的带隙理论，对夹心式换能器进行优化。在传统夹心式换能器基础上，通过将换能器的前盖板加工成二维声子晶体结构，使得共振频率处于二维声子晶体结构前盖板的带隙范围内，从而达到抑制换能器横向振动的目的。这种结构的纵向振动的夹心式换能器的振动模态更加的单纯，对换能器的振动特性有明显的优化。本文讨论了散射体的半径大小及高度对换能器的共振频率、声子晶体结构前盖板带隙以及换能器的振动特性的影响，得出了如下结论：

(1)二维声子晶体结构前盖板对换能器的共振频率存在影响，随着散射体半径的增大，共振频率也在变大，随着散射体高度的增加，共振频率先增加后减小；

(2)通过有限元仿真法计算的加速度响应曲线可知二维声子晶体结构前盖板存在包含换能器共振频率的带隙范围，并且带隙的范围会随着散射体的半径和高度发生变化；

(3)在换能器前盖板前端开圆柱形孔径形成的二维声子晶体结构能够有效抑制大尺寸夹心式换能器的横向振动，优化换能器的振动性能。

大尺寸夹心式换能器的耦合振动是在横向尺寸过大时会出现的一种现象，对换能器的工作效率会造成很大的影响，本文基于二维声子晶体结构带隙的有限元法研究为抑制功率超声换能器的耦合振动提供了一种新的方案，在实际应用中具有重要意义。