双横波声速法检测单向受压混凝土构件永存应力*

郑康琳 张劲泉 王 陶 赵尚传 樊 平 王 磊 李 萍

(交通运输部公路科学研究所 北京 100088)

0 引言

永存应力是指由结构自重及其他恒载效应产生的结构内部持续稳定的应力，应力超限会导致结构破坏并影响结构安全，因此对结构永存应力的检测十分必要。目前检测混凝土构件永存应力的方法分为有损检测和无损检测两类，其中超声检测是无损检测中最主要的方法之一，其理论基础为声弹性理论，利用声波在构件中传播的波速、波频、振幅等声学参数与应力的相关性来检测结构永存应力。虽然早在1953年Hughes 和Kelly 就已经提出了声弹性理论[1]，但直到现在应用声弹性理论检测混凝土构件永存应力的研究仍处于探索阶段。1998年，朱金颖等[2]通过实验得出波速对混凝土构件中的应力变化敏感度较低，在70% 的极限应力范围内，波速基本保持稳定。2005年，陈立新等[3]通过实验得出声学参数与混凝土应力较为敏感时的骨料粒径、骨料种类(卵石)、水灰比和砂率等因素之间的关系。同年，林军志等[4]研究混凝土应力与超声波波速、首波振幅、最大振幅等声学参数的相关性。2007年，雷正伟等[5]通过实验得出温度对声速的影响量级与应力的影响量级接近，进行应力定量计算需考虑温差因素。2010年，Lillamand 等[6]研究混凝土材料在轴向压力作用下的声弹性效应，得出与应力水平敏感性最大的是沿加载方向偏振的纵波和横波的结论，并成功得到混凝土试件的声弹性系数。2012年，刘新建等[7]基于模型实验，详细分析不同种声学参数与应力的相关性，并通过实验着重研究超声波信号加权瞬时振幅峰值、加权边际谱面积、加权瞬时能量谱面积随应力的变化情况。2017年，刘宏翔等[8]通过实验测试不同龄期不同应力状态下混凝土试块的声速值，分析了超声波波速随混凝土龄期的变化规律，并建立了超声波波速与应力之间的回归曲线。

纵观该领域的研究现状，目前对超声检测混凝土构件永存应力的研究主要集中在各种单项声学参数(声速、振幅、直达波频率等)与应力相关性上。但在实际应用中这些声学参数对应力的变化不够敏感，检测结果容易受到诸多外界因素(温度、湿度、混凝土的配比等)的干扰，这些因素引起的声学参数的变化常常远大于结构应力所引起的变化，“应力效应”常被“噪声效应”所淹没。因此目前以单项声学参数检测混凝土结构永存应力的方法仅为理论的可能性，远未达到实用的程度。

本文提出了一种超声检测单向受力混凝土构件永存应力的方法，该方法采用测试结构受载后的第一波速V1(传播方向与应力σ方向垂直，质点振动方向与应力σ方向平行的横波波速)和第二波速V2(传播方向及质点振动方向均与应力σ方向垂直的横波波速)，以V1、V2构建组合声学参数“(V21-V22)/K′′(K为材料常数)来检测单向混凝土受力构件的永存应力σ。该声学参数用于检测混凝土单向受压构件永存应力的效果与使用单一声速参数相比，对应力的敏感性有所提高，受混凝土黏滞性及材质离散性的影响更小，并且测试结果基本不受温度和湿度变化的影响，以下对该方法的原理及实验验证情况进行详尽阐述。

1 方法原理

根据声弹性理论[9]，各向同性固体介质在单向应力σ作用下，介质中声速变化情况不仅与介质应力大小和方向有关，还与声波传播方向、声波质点振动方向有关。对于横波来说，声波传播方向垂直于介质应力σ方向、质点振动方向平行于应力方向的横波波速V1及声波传播方向和质点振动方向都垂直于介质应力方向的横波波速V2与介质应力σ的关系式为

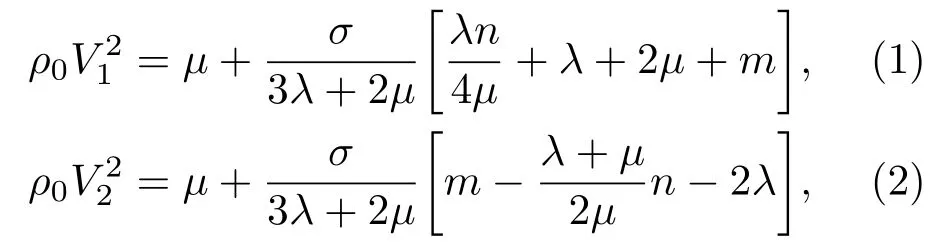
其中：ρ0为零应力下介质材料的密度；σ为介质应力；λ、μ分别为介质材料Lame 常数；m、n分别为介质材料的Murnagham三阶弹性常数。

从式(1)、式(2)可以看出：在应力σ=0的情况下，横波声速V1、V2均为；在应力σ≠0的情况下，不同传播方向及不同偏正方向的声速表现出不同程度的差异。由公式(1)～(2)可以得到：

令：

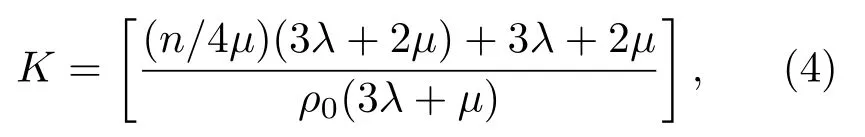
则：

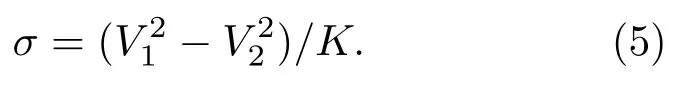
因K为与材质特性有关的常数，依据式(5)，通过测量波速V1、V2，即可算出应力σ。设t1、t2分别为横波V1、V2在被测构件中的传播时间，设Δt=t2-t1为V1、V2传播的时间差，在测量V1、V2时因入射波探头和接收探头位置相同，所以V1、V2的传播距离及路径相同，设声波传播距离为l，因V1、V2为间接测出量，t1、t2为直接测出量，采用参数“Δt”代替“(V21-V22)”。以下为推导过程：

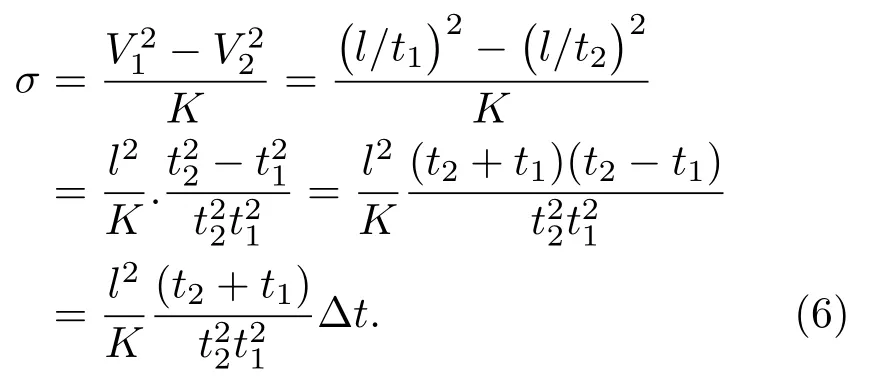
因t1、t2相对变化都较小，故t2≈ t1≈(t2+t1)/2=t0，所以由公式(6)得

对一个确定的测试构件，K、l都是常数，t0的相对变化值很小，近似为常数，所以结构永存应力σ大小取决于Δt。依据公式推导的前提条件可知本检测方法适用条件如下：

(1)测试对象为单向受力构件，且应力的方向已知；

(2)测试对象在在无应力情况下声波在各个方向的传播速度相同；

(3)测试对象应力值处在材料弹性范围内，结构不能出现裂缝及过大的非线性形变等现象。

与使用单一声学参数相比本方法具有以下优点：

(1)理论上参数Δt零应力值为零，易于标定。当σ= 0 时，对于各向同性介质t1=t2=t0，则Δt=t2-t1=0。而其他单一声学参数零应力值一般不为零，检测时则需要标定零应力值，标定过程中会产生误差。

(2)参数Δt对应力σ有更高的敏感性。Δt=t2-t1=(t2-t1)-(t0-t0)=(t2-t0)-(t1-t0)=Δt2-Δt1，依据声弹性理论，当σ增加时，t1减小、t2增加，即Δt1与Δt2反号，在相同的应力变化情况下，|Δt|=|Δt1|+|Δt2|，由此得出Δt较单一参数t1、t2对应力有更好的敏感性。

(3)参数Δt能够消除温度、湿度等环境因素对测试结果的影响。环境因素(温度、湿度等)会显著影响声学参数的变化，但这种影响是各向同性的，即对t2、t1影响基本相同，这种影响在参数Δt=t2-t1做差值的时候即可消除。

(4)横波双声速法测量时全程无需改变探头位置，可避免探头移动产生的测试误差。理论上双声速法检测永存应力既可采用纵波也可采用横波，采用纵波法分别测量V1、V2时需要改变入射探头和接收探头的位置，由于混凝土材质的离散性，这个过程会产生较大不可预知的误差；采用横波法时测量全程无需改变探头位置，只需转动探头的角度，这避免了移动探头所带来的巨大误差，这也是双横波声速法最大优势，所以本文采用双横波声速法。以下通过实验对本方法进行验证。

2 实验过程与结果讨论

2.1 实验方法

本实验中制作混凝土立方体试件作为实验对象，试件尺寸为15 cm×15 cm×15 cm，共计17个，依次标记为1#～17#，分别制作C30、C40、C50 三种标号的试件，1#～6#、12#试件混凝土标号为C50，7#～9#、14#、17#试件混凝土标号为C40，10#、11#、13#、15#、16#试件混凝土标号为C30。超声波测试设备采用RITEC RAM-5000 SNAP 非线性高能超声测试系统，数据采集采用MSO4104B-L 示波器，探头采用奥林巴斯V150-RM 横波探头(中心频率为0.25 MHz)。本次研究进行了3 个方面验证实验：

实验一 应力效应实验。共进行11 组，试件编号为1#～11#，实验目的是验证试件应力与声学参数之间的关系(公式(7))。本实验中，在试件顶底面用液压设备均匀施加均布压力F，设试件横截面为S，则试件内部压应力为σ=F/S，在实验的过程中通过调节均布力F的大小来改变构件内部应力σ，如图1所示。探头布置采用对测法，S和R分别横波发射探头和接收探头，S 与R 连线方向与应力σ方向垂直(如图1所示)。每次测试时，先把横波发射探头和接收探头声波质点振动方向调整为与应力平行方向，测得声速V1在构件中传播的时间t1，然后保持探头中心点位置不变，把发射探头和接收探头同方向旋转90°再同法测试，可得声速V2在构件中传播的时间t2。改变均布力F的大小，重复上述步骤，就可以测出不同应力σ状态下的t1、t2、V1、V2及Δt。然后依据实验数据归纳总结出Δt与应力σ之间关系曲线。在应力加载过程中，试件的温度、湿度均保持不变。实验中入射波为1 周期的正弦波(如图2所示)，频率为0.15 MHz，接收波信号采用连续采样，采用频率为100 MHz。t1、t2的取值方法分别为V1及V2的接收波首波零点与发射波首波零点之间的时间差，如图2所示。

图1 试件加载及声速测试示意图Fig.1 Schematic diagram of test piece loading and sound speed test

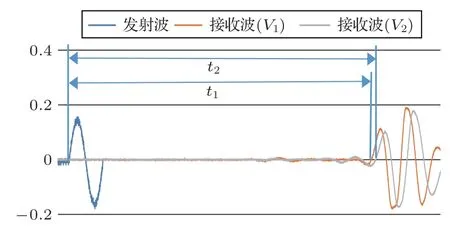
图2 实验中t1、t2 取值方法示意图Fig.2 Schematic diagram of short-cut process method of t1 and t2 in the experiment

实验二 温度效应实验。共进行3 组，试件编号为12#～14#，实验目的是验证试件温度对声学参数的影响。实验中保持试件为零应力、干燥状态，初始温度为室温(27 ℃)，按实验一的方法测出构件初始温度下t1、t2，然后把试件放入加热箱内，均匀加热到60 ℃后取出，同法测出试件60 ℃状态下t1、t2。对比试件加热前后两种不同温度状态下声学参数的变化，分析温度因素对声学参数影响。

实验三 湿度(含水率)效应实验。共进行3组，试件编号为15#～17#，实验目的是验证试件湿度(含水率)对声学参数的影响。实验中保持试件为零应力、室温(27 ℃)的状况下，初始状态为干燥状态，按实验一的方法测出t1、t2的值，同时测量出干燥状态下试件重量m0，然后把试件放入水中浸泡24 h后取出，测出浸泡后的质量m，由m0与m推算出试件的含水率(m-m0)/m×100%，最后测出试件含水时t1、t2的值。通过对比试件干燥与含水两种状态下声学参数的变化，分析湿度(含水率)因素对声学参数的影响。

2.2 实验结果及讨论

2.2.1 应力效应实验结果及讨论

图3为本次实验各试件应力与声学参数关系实测结果。

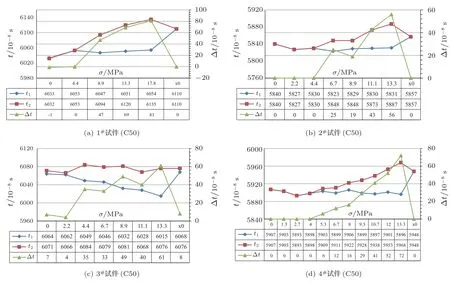
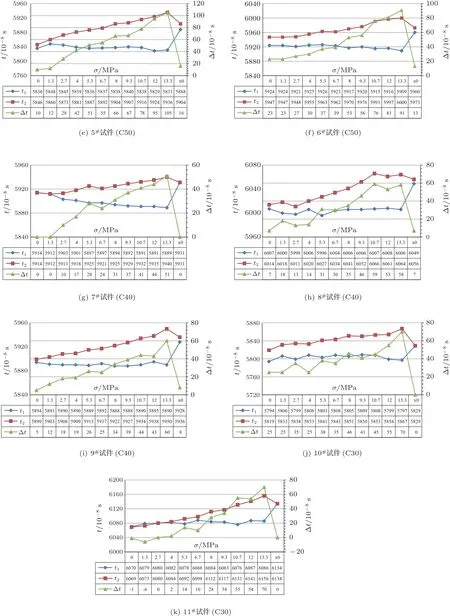
图3 应力效应实验试件σ-t1、t2、Δt 受载历程曲线Fig.3 Loading history curve of σ-t1、t2、Δt of stress effect test specimen

根据以上实验结果对以下6个问题进行讨论：

(1)关于σ-Δt线性相关性问题

引入线性相关系数

式(8)中，R为参数σ、Δt之间的线性相关系数；σi、Δti分别为参数σ、Δt的样本值；、分别为参数σ、Δt的样本值平均值。

参数R反映统计参数σ、Δt之间的线性相关性，R值越接近1，则参数之间线性相关性越好，参数图形越接近直线。表1列出了实验中应力σ值与对应声学参数Δt实验值之间的线性相关系数。

从表1中可以看出，实验中所有试件σ-Δt之间线性相关系数的平均值为0.953，非常接近1，说明整体上参数σ、Δt实验值之间具有很好线性关系。实验结果还显示，在低应力阶段所有试件σ-Δt之间线性相关系数的平均值为0.755，这说明在低应力阶段σ-Δt之线性符合性较差；在高应力阶段时，所有试件σ-Δt 之间线性相关系数的平均值为0.945，σ-Δt之间线性符合性较好。推测出现这种现象的可能原因为：混凝土是一种混合物结构，内部存在较多气孔及其他微小蓬松结构，在较低应力阶段由于这些蓬松结构尚未被“压实”会出现较明显的“非线性”，这种“非线性”的过程会导致结构的实际特性与理论预测出现较大差异。以上分析只是基于一种可能性的推测，产生这种现象的确切原因还需要后续研究进行进一步的探索及验证。

表1 应力效应实验混凝土试件应力σ 与声学参数Δt 实验值之间线性相关系数Table 1 Linear correlation coefficient between stress σ and acoustic parameter Δt of concrete specimen in stress effect test

(2)关于零应力下参数的初值问题

对于各向同性介质，声学参数Δt在零应力状态下的值为零，但实际中的介质并非完全各向同性，因此Δt在零应力状态下测试值并不严格为0。本实验中未加载情况下的试件参数Δt初值介于-1～25×10-8s (如表2所示)，与满载应力状态下的参数比值平均为9%。可见用本方法检测结构永存应力时该因素会导致测试结果产生一定的误差，当测量较小应力时其导致相对误差会较大，当测试应力增大时，其导致相对误差会减少。

表2 应力效应实验混凝土试件加载前零应力状态下参数Δt 初值Table 2 Initial value of parameter Δt under zero stress state of concrete specimen in stress effect test before loading

(3)加载卸零后参数的残值问题

在本实验中随着试件压应力σ增加，t1呈减小趋势，t2呈增加趋势，即随着压应力σ增加，V1增大、V2减小，这与声弹性理论模型基本符合。但应力卸零后，Δt1、Δt2仍有较大的“残留值”(如表3所示)，其中Δt1相对残留平均值为-458%，Δt2相对残留平均值为60%。而Δt在应力卸零后基本恢复到零(如表3所示)，相对残余平均仅为-2.9%。实验中参数在加载后卸零的残值现象说明双横波声速组合参数((V21-V22)/K或Δt)与应力σ之间有更强的相关性，用其作为声学参数测量单向受压混凝土构件永存应力较单一声速参数更具可行性。采用单一声速(V1或V2)变化值来检测混凝土构件永存应力的方法是不具可行性。

表3 应力效应实验混凝土试件加载后应力卸零后参数Δt1、Δt2、Δt 相对残余值Table 3 Relative residual values of parameters Δt1、Δt2 and Δt after stress unloading of concrete specimen in stress effect test

(4)参数对应力的敏感性问题

在本实验应力作用下，应力σ与时程差Δt近似成正比关系，应力σ与Δt之间有较强敏感性，σ/Δt的值在实验最大应力状态下介于0.13～0.26 MPa/10-8s 之间，Δt在100 MHz 的采样频率下对应力σ具有较好的敏感性。

(5)材料参数K的离散问题

试件的材料常数K的计算采用公式(7)变换得到：

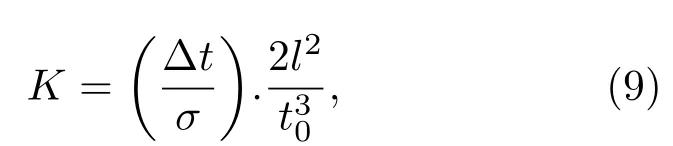
式(9)中，2l2/t30均为常数，取值与公式(7)相同，(Δt/σ)取值时看作一个整体，其取值为试件σ-Δt实验值线性回归趋势线的斜率倒数。另外引入统计参数相对标准差：

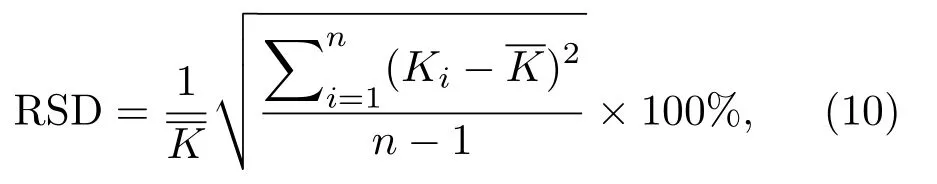
式(10)中，RSD (Relative standard deviation)为材料常数K样本值的相对标准差，其反映参数样本值的相对离散性；Ki为材料常数K样本值，由公式(9)计算可以得到；为材料常数K样本平均值。

试件材料参数K计算结果如表4所列。从表4中可以看出实验中实测C50 试件材料常数K样本均值为0.0112，相对标准差为22.8%；C40 试件材料常数K样本均值为0.0083，相对标准差为4.2%；C30试件材料常数K样本均值为0.0083，相对标准差为52.9%；全部试件材料常数K样本均值为0.0099，相对标准差为27.8%。总体来看，实验中试件的材质常数K样本值离散性较大。从试件混凝土标号对材料常数影响来看，实验中材料常数K样本均值有随试件混凝土标号降低而减小的趋势。

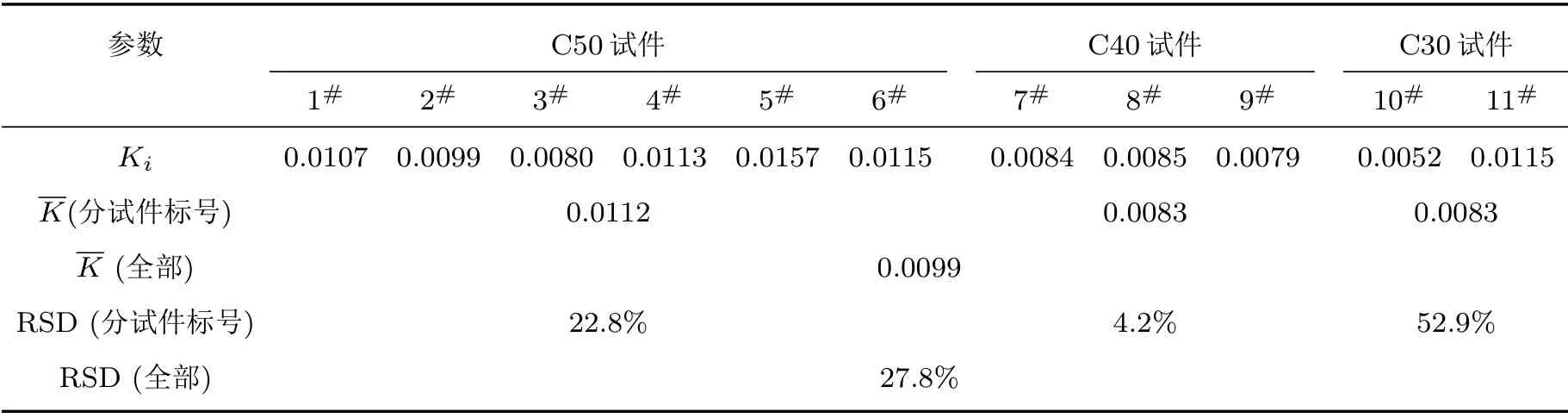
表4 应力效应实验混凝土试件材料常数K 测试值Table 4 Test value of material constant K of concrete specimen in stress effect test

(6)实验值总体的离散问题

图4(a)～(c)为按强度等级C50、C40、C30 把试件为3 组，分别对每组试件σ-Δt实验数据进行线性回归分析的结果。图4(d)为在不区分试件混凝土标号情况下对全部试件σ-Δt实验数据进行线性回归分析的结果。

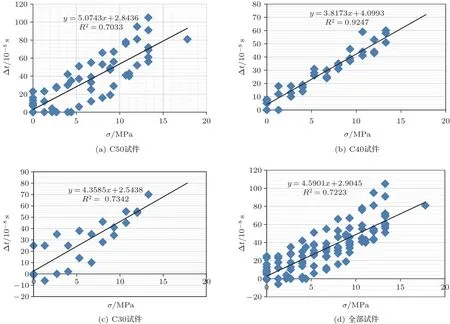
图4 试件σ-Δt 实测值线性回归趋势Fig.4 Linear regression trend line of specimen

从分析结果看，不同试件间的实验数据具有较大的离散性。在应力大于10 MPa 的情况下，试件实际实验值与回归曲线值相对误差范围C50 组混凝土介于-34%～51%，C40 组误差介于-13%～34%，C30 组误差范围介于-9%～16%，不区分混凝土标号全部试件组误差范围介于-27%～67%。从实验结果看在现在的实验条件下，实验数据的离散性较大，实验结果离实际应用仍有较大差距。

2.2.2 温度效应实验结果及讨论

表5为构件温度与声学参数关系实验结果。

表5 温度与声学参数关系实验结果Table 5 Experimental results of relationship between temperature and acoustic parameters

从以上实验结果可以看出：

(1)试件温度变化显著引起了声波传导时间t1、t2的变化，t1、t2的变化主要由声速V1、V2变化引起(经测算实验中温度引起试件长度的变化可以忽略不计)。经测算，实验二中每1 ℃的温变引起的超声传播时间t变化值约4×10-8s，这与实验一中1 MPa应力效应大约相当。可见温度是超声检测永存应力中的一个不可忽视的因素。

(2)虽然试件温度的变化会显著引起t1、t2的变化，但t1与t2为同向变化，Δt=t2-t1做差值时消除了温度引起的变化，因此声学参数Δt的基本不受温度变化的影响。所以用声学参数Δt检测结构永存应力可“剔除”温度因素的影响。

2.2.3 湿度(含水率)效应实验结果及讨论

表6为构件湿度(含水率)与声学参数关系实验结果。

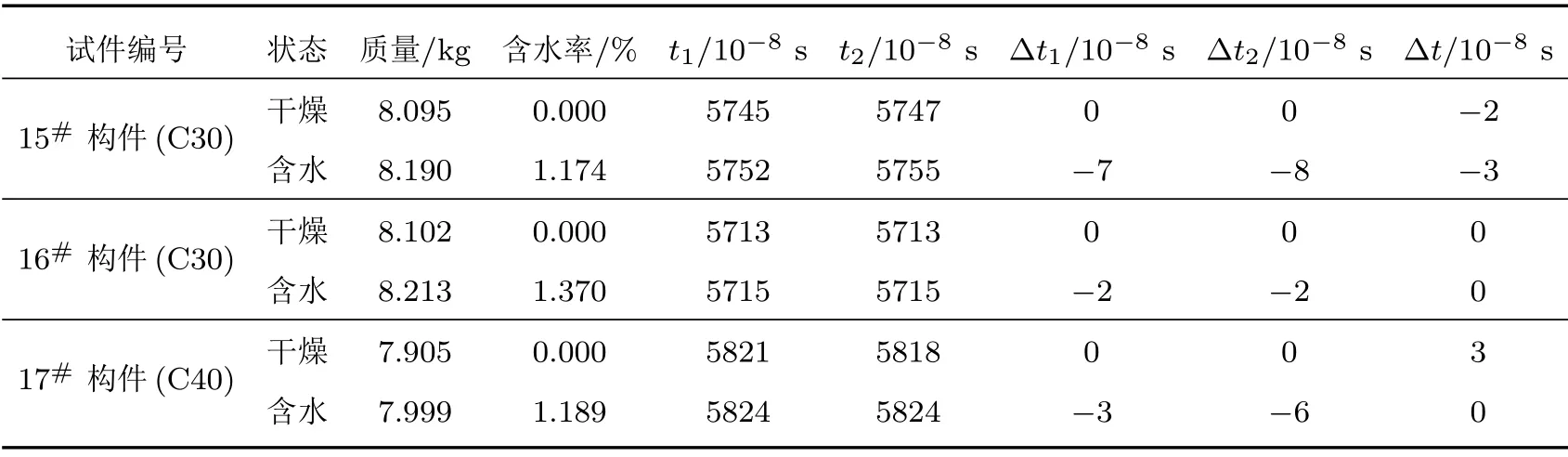
表6 试件湿度(含水率)与声学参数关系实验结果Table 6 Experimental results of relationship between moisture content and acoustic parameters

从实验结果可以看出，试件含水率的变化未引起t1、t2显著变化，亦不会引起Δt的变化。

3 结论

本文所提方法具有参数零值易于确定、参数对应力的敏感性更高、能够剔除温度等环境干扰因素的影响、能够排除混凝土黏滞性对参数的影响、测定双声速时无需移动测试探头等优点。但同时也存在实验中试件实测材料常数K的离散性大、部分试件零应力下参数Δt不为零等问题，这些不利因素致使目前尚不能制定出普遍适用的混凝土构件σ-Δt关系曲线，因此该方法距离实际应用还有较长的一段路要走。针对目前存在的问题，下一步研究需要努力寻找产生问题的原因，找出消除不利因素的可行方法。