基于一维卷积神经网络的化爆和地震次声分类*

谭笑枫 李夕海 刘继昊 李广帅 于晓彤

(火箭军工程大学 西安 710025)

0 引言

作为国际监测系统(International Monitoring System，IMS)四种技术中的一种，次声波为有效监测大气层核试验以及地面或水面核爆炸提供了重要帮助[1-2]。次声监测技术同样可以作为火山喷发、海啸、天然地震等地质灾害的重要监测手段[3]。

次声事件的监测与识别研究应用广泛，是核爆探测、自然灾害预测、大气环境研究、生物效应等方面研究的重要组成部分[4-6]。次声事件的监测和分类识别工作往往是一起的，为提升核爆和地质灾害的监测能力，采取相应措施从而正确识别次声事件，是有效的途径之一[7]。因此，开展次声事件的分类研究，对于国家安全和地球物理研究具有重要意义。

20世纪50年代以来，关于次声事件的分类任务，国内外学者对此进行了深入的探索，主要利用声学信号处理理论，分别在时域频域提取特征，进而用于分类识别。然而，由于次声的多径效应，导致原来的信号失真，或者产生错误，分类识别率不高。为提高识别率，需要多特征、复杂特征进行综合识别。在国际上，Chilo 等[8]等指出小波变换是获取次声事件“指纹”的方式之一。Cannata等[9]成功运用聚类、分类算法结合特征提取技术实现对意大利埃特纳火山口的定位。Thomas 等[10]将分类算法和次声阵列检测法结合起来，对雪崩灾害实现预警，其预警错误率可降至0.1。在国内，姜楠等[11]提出将次声信号的固有模态函数(Intrinsic mode function，IMF)的分量比作为特征，再采用支持向量机(Support veotor maohine，SVM)完成分类，可对天然地震、火箭发射、管道爆破进行有效分类识别。杨婷婷等[12]将次声信号模态分解(Empirical mode decomposition，EMD)后的奇异谱熵作为特征，采用最小二乘支持向量机(Least squares support vector machine，LSSVM)作为分类器，能够对化学爆炸和矿道爆炸完成较好分类识别。明舒晴[13]提出IMF 显著频率特征提取方法，采用聚类算法，实现对火山喷发、地震等3 类地灾次声事件的有效分类。随着人工神经网络的兴起，复杂特征与人工神经网络相结合的方法逐渐应用到了次声事件的分类识别中，对于次声事件识别效果的有效提高提供了帮助[14-15]。

尽管如此，由于多径效应以及不同类别次声事件信号差异性表征的困难，直接利用现有数据进行分类识别，会出现次声信号特征聚集性不强、识别率不够高的结果。为提高识别率，传统分类方法需要进行多步数据预处理工作提取出较优的特征组合，并选择合适的分类方法实现次声事件的分类识别，这样的信号处理过程相对复杂，这对次声事件的分类工作提出了挑战。针对这一问题，本文考虑引用深度学习(Deep learning)技术来解决。近年来，深度学习在人工智能计算上成效突出。作为深度学习的一种，卷积神经网络(Convolutional neural networks，CNN)具备强大的特征提取和学习的能力，能够提取到人工无法描述的特征，并完成分类识别，在数字识别、图像分类与识别、噪声去除等领域上都得到了很好的应用[16-18]。基于CNN 强大的特征提取功能，本文将数据预处理过程简化，提取简单的特征作为CNN 的输入，利用CNN 完成特征提取、模型训练和分类识别的工作。

本文利用Welch 功率谱变换进行简单的特征提取，采用改进CNN 完成分类工作，并基于收集整理的包含815个化学爆炸(简称化爆)和天然地震(简称地震)次声信号数据集，使用BP 网络和一维LeNet-5网络进行分类对比分析。

1 数据集及预处理

1.1 建立数据集

由于条约组织有较多的次声台站用于获取次声信号，因此，本文统一使用从CTBTO官网上收集到的次声信号数据进行分析，选用信道为BDF格式的数据。其主要原因是基于其他信道格式(BD、SD)的数据量较少，提取到的特征参数不能够充分表征次声事件，也不利于分类判别时训练及测试样本的构造。针对BDF格式的数据具体操作如下：

步骤1 读取从CTBTO 官网上下载的原始数据(.w文件)，寻找信道为BDF格式的数据；

步骤2 统一采样频率，将采样频率高于20 Hz的数据进行重新采样；

步骤3 将采样点数不够的数据进行人为的补齐或去除；

步骤4 判断提取到的台站数据信息中有无重复成分，重复予以去除，不重复予以保留。

经过上述步骤，得到次声信号共2512 个，包含化爆次声信号2107 个、地震次声信号405 个，其中每个信号包含完整的事件，长度为3000 个点。为了保证数据平衡，采用降采样的方法，从2107 个化爆次声数据中随机抽取410 个样本，与405 个地震次声数据组成815 个次声信号的原始数据集。其中的化爆和地震次声事件波形示意图如图1所示。

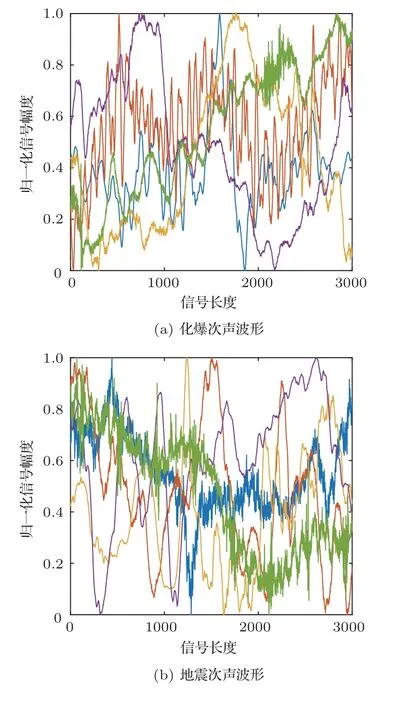
图1 两类次声事件波形示意图Fig.1 Two types of infrasound event waveform diagram

利用815 个次声事件信号建立数据集。数据集包括训练集、验证集和测试集，分别用于网络模型的训练、验证和测试。3个集合分别包含地震样本和化爆次声样本。在保证训练集、验证集和测试集中两类样本数量大致相同的情况下进行随机抽取，按照训练集样本数量占比80%、验证集和测试集样本数量各占比10%，即三者比值为8:1:1建立数据集。

1.2 数据预处理

1.2.1 提取功率谱特征

功率谱作为声学信号分析的重要方法，表示了信号功率随着频率的变化关系，将其作为特征能够更好地凸显出地震和化爆信号的差异。本文采用Welch平均周期法[19]，对次声事件原信号进行功率谱估计。把信号长度为n的数据分成M段，其中每段长度为N(允许存在重叠的部分)，对每段信号分别完成功率谱计算，取其结果的平均值得到功率谱估计结果。根据经验，采用汉宁窗代替矩形窗，用于解决旁瓣过大造成的功率谱的失真现象。每段功率谱可以表示为[20]

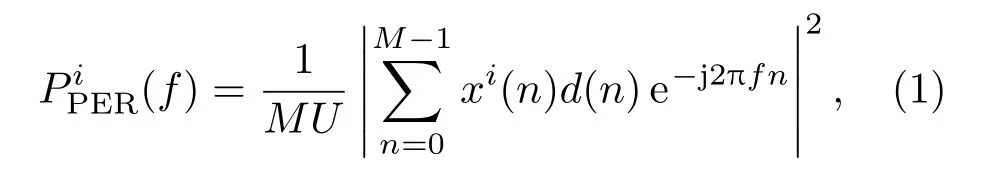
其中，n代表次声信号采样数据点数，U表示归一化因子，目的是为使得到的功率谱为接近无偏估计。具体表示为

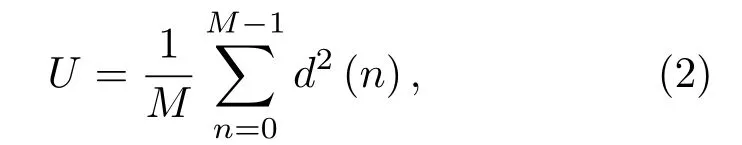
其中，d(n)为汉宁窗，因此，平均功率谱可以由式(3)表示：

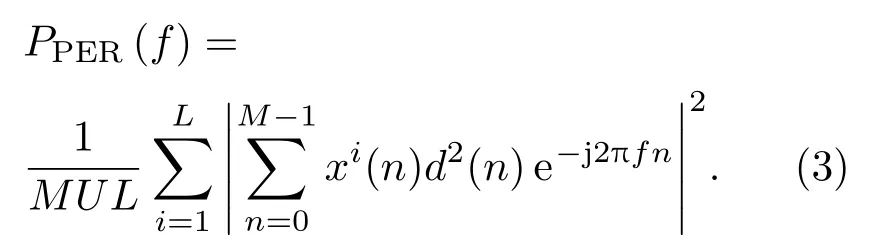
可以把功率谱转换为分贝表示[21]

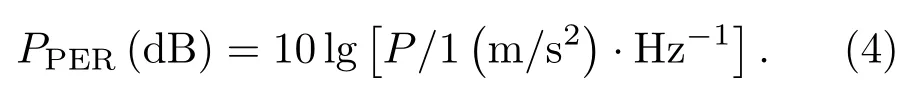
通过上述方法，可以将次声信号原始数据进行功率谱估计。本文对信号进行平均采样，每段次声信号x(n)为3000 个采样点，将数据进行分段处理。经过功率谱计算后，就把3000 个点的时域次声信号x(n)处理为频率范围在0-10 Hz 的功率谱值。图2即表示化爆和地震次声的Welch功率谱示意图。

从图2可以看出，化爆的功率谱值主要集中在0.3～0.6 之间，地震的功率谱值主要集中在0.35～0.65 之间，两类事件的功率谱值在范围和趋势上存在差异。

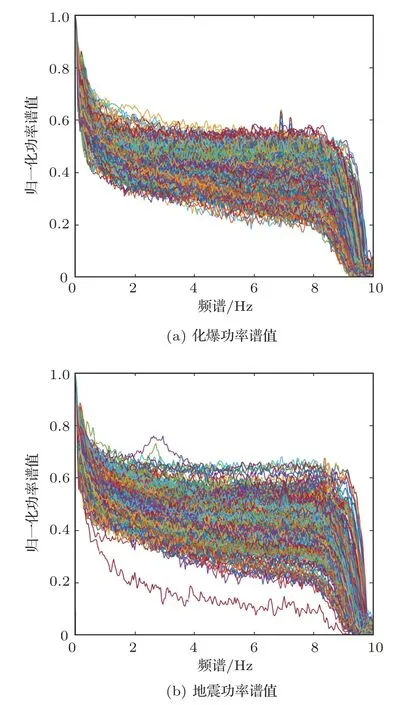
图2 Welch 功率谱示意图Fig.2 Welch power spectrum diagram

将1.1 节建立的数据集中的次声数据进行Welch 功率谱估计特征提取，得到所有次声信号样本的功率谱特征。

1.2.2 提取IMF分量比特征

将次声信号进行EMD 分解，可以得到次声信号的n阶IMF分量和一个残差量。计算每个IMF分量的能量，可以筛选出能量最大的前m个分量，m个分量的总能量大于等于整体能量的85%以上。将前m个分量的能量两两相比，可以得到一个新的特征向量，即IMF分量比[11]。

具体IMF分量比特征提取的步骤如下：

(1)将次声信号进行EMD 分解，得到n个IMF分量和1个残差量；

(2)计算每个IMF分量的能量；

(3)将得到的能量值两两相比，得到IMF 分量比。

整个过程如图3所示。

图3 IMF 分量比特征提取和分类过程Fig.3 IMF component ratio feature extraction and classification process

图4 IMF 分量比特征示意图Fig.4 IMF component ratio feature diagram

1.2.3 提取IMF奇异谱熵特征

IMF 奇异谱熵就是将IMF 分量进行相空间的重新构建，获得一个轨迹矩阵，然后对该矩阵进行奇异值分解，按照一定条件选择前m个最大值，计算奇异谱熵值。具体操作如下[12]：

(1)在(N -n+1)×n维的相空间中嵌入IMF分量cj(t)，得到轨迹矩阵：

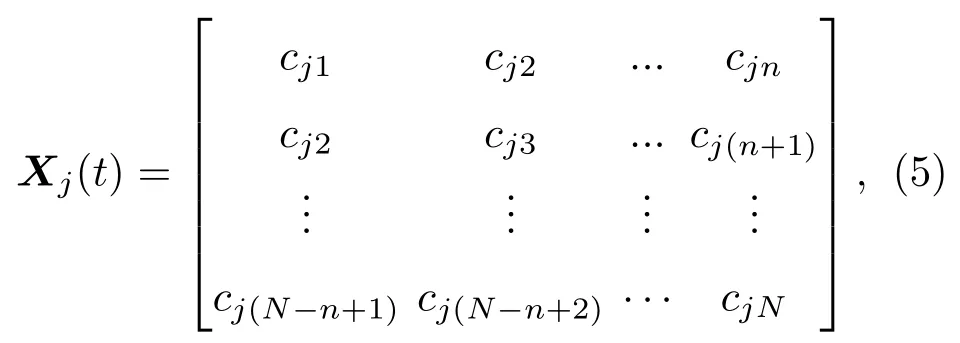
其中，n代表嵌入向量的维数；N代表采样点数；cji(t)为第j阶IMF分量的第i个采样值。

(2)计算Xj(t)的奇异值。Xj(t)可以被分解为两个相互正交的矩阵U、V和一个对角矩阵Λ的乘积的形式(三个矩阵的维度分别为(N-n+1)×(N-n+1)、n×n和(N-n+1)×n)。所求的信号奇异值，即为Λ中主对角线上的元素λb，其个数l需要满足公式

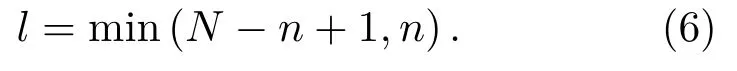
因此，可以得到奇异值分解的表达式：

(3)选择特征维数。基于降维和信息量两个角度综合考虑，既要尽可能选择少量的维度，又要保证保留较多的信息量。因此只选取前q个最大的对角矩阵的元素作为特征，但前q个元素需要包含信号85%以上的信息，即q需要满足

(4)计算奇异谱熵：

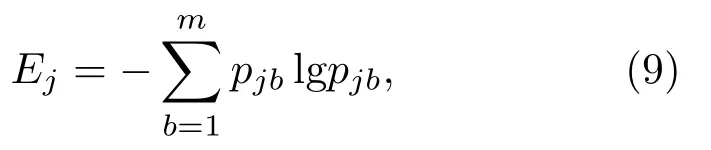
本文使用IMF 奇异谱熵前二维特征作为功率谱的对比特征，特征如图5所示。

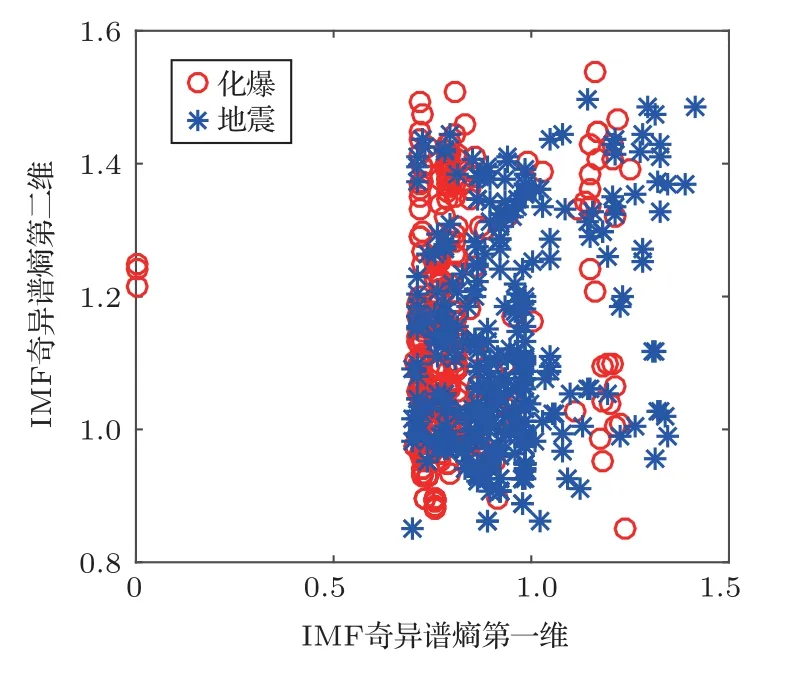
图5 IMF 奇异谱熵特征示意图Fig.5 IMF singular spectural entropy feature diagram

2 网络模型构建

2.1 BP网络

BP 神经网络是1986年Rumelhart 和McClelland 等提出的，是一种基于误差逆传播算法训练的多层前馈神经网络，用于前向多层神经网络的反向传播学习算法，也是神经网络模型中应用最广泛且最重要的一类学习算法。它具有理论依据坚实、推导过程严谨及通用性好的优点，是深度学习算法的基础。

用BP 神经网络对次声信号进行分类识别，需要确定输入层、输出层和隐藏层节点数。输入层节点数I为输入信号特征的长度，输出层节点数O为数据类别数，本文为实现地震和化爆分类识别，即输出节点数为2，隐藏层节点数根据经验公式(10)确定：

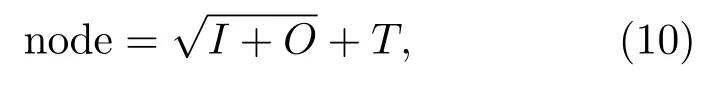
其中，node为隐藏层节点数量，I和O分别为输入层和输出层的节点数量，T为调节参数，取值范围为1至10。本文中T分别取值1、4、10，当输入层为功率谱信号(257 个点)时，隐藏层节点数node 分别取值17、20、26。

2.2 LeNet5网络

LeNet-5 网络是Lecun[22]在1998年提出的经典的CNN，在手写体字符识别上效果显著。如图6所示，LeNet-5 网络总共分为5 层，分别由两组卷积层和池化层以及一个全连接层组成。卷积层完成特征的提取工作，池化层通过下采样实现减少网络参数以减小计算量，全连接层能将学到的特征映射到样本标记空间，即起到“分类器”的作用。LeNet-5网络非常简单，卷积层数和参数相对较少，学习时间相对较快。作为一个十分成功的深度CNN模型，目前多个方面得到应用，例如在银行系统中用于识别支票上的数字等。

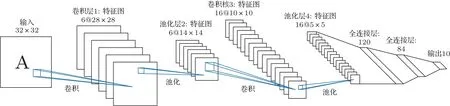
图6 LeNet-5 网络结构Fig.6 LeNet-5 network structure

由于次声信号为一维数据，为适应次声数据处理，在LeNet-5网络中，统一采用一维卷积核实现卷积操作，即卷积层卷积核由5×5 改为1×5，池化层由2×2改为1×2。以功率谱信号作为输入为例，并将二维LeNet-5 网络改变成一维卷积网络后，其网络结构如图7所示。

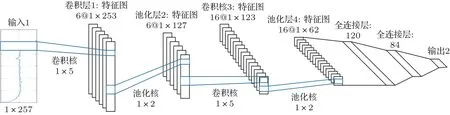
图7 一维LeNet-5 网络结构Fig.7 1-D LeNet-5 network structure

2.3 改进的CNN

由于样本本身数量有限，采用过于深层的卷积神经网络训练容易导致过拟合的现象。本文采用浅层的CNN 作为研究对象，尽量精简网络结构，达到较少的样本也能实现深度学习的目的。选用网络结构较为简单的LeNet-5神经网络结构作为基础网络进行设计改进。本文改进之后的网络结构模型如图8所示。

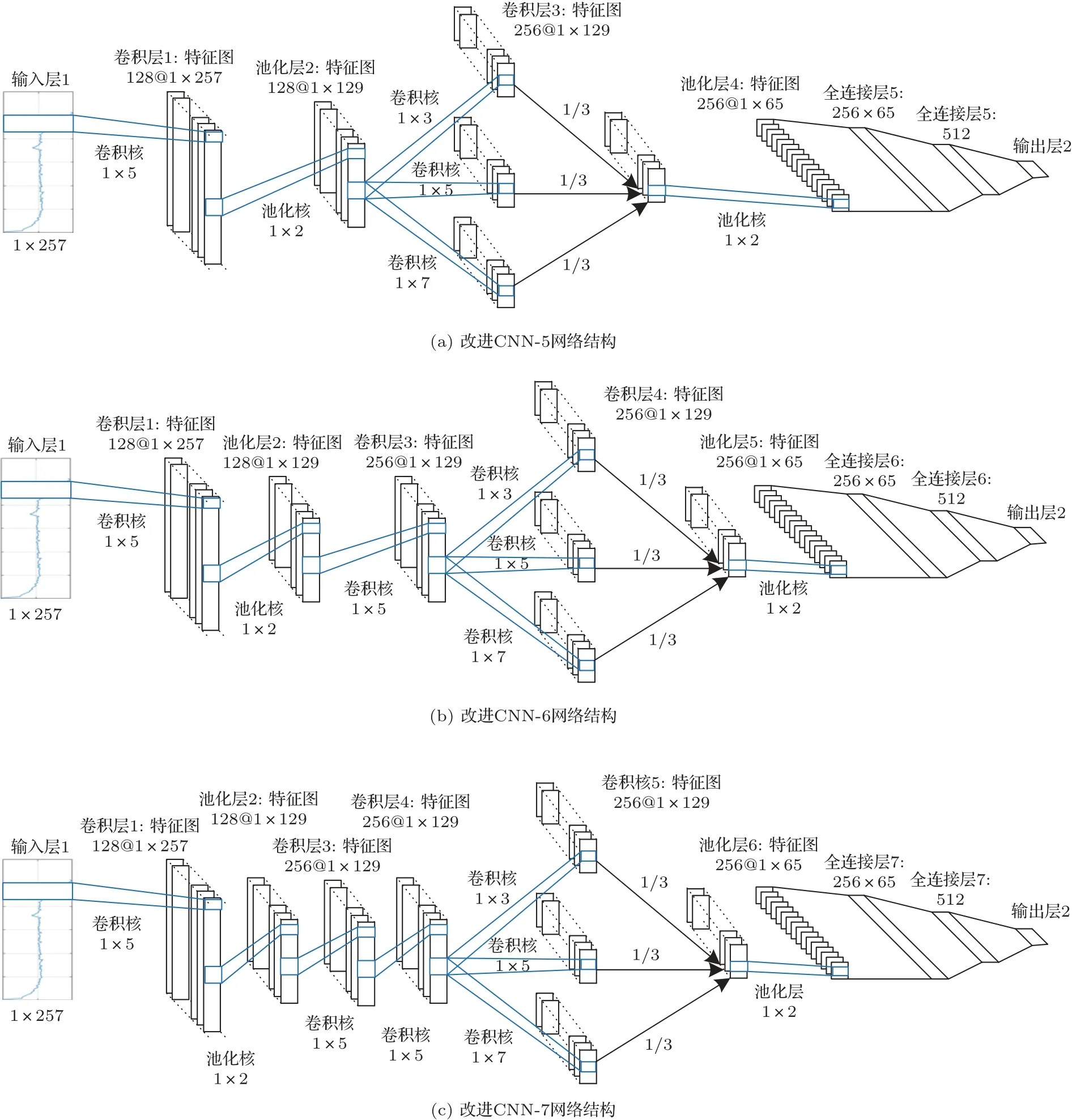
图8 改进CNN 网络结构Fig.8 Improved CNN network structure

如图8(a)所示，改进CNN-5网络第一层卷积层输入通道数为1、输出通道数为128，卷积核大小为1×5，输入和输出数据大小都为1×257；第二层池化层输入和输出通道数均为256，输入数据大小为1×257，输出数据大小为1×129；第三层卷积层输入通道数为128，输出通道数为256，卷积核采用1×3、1×5、1×7三路卷积，输入输出数据大小都为1×129；第四层池化层池化层输入和输出通道数均为256，输入数据大小为1×129，输出数据大小为1×65；第五层为全连接层及分类器。

相比“LeNet-5”网络，本文主要做了以下三个方面的改进：

(1)改变卷积核参数，其中第一层卷积层保持不变，依旧采用1×5的大小，第三层运用分路卷积、加权融合的思想，分别使用1×3、1×5、1×7 的卷积核，卷积结果分别乘以系数1/3，再将结果相加得到第三层卷积层特征图，池化层统一使用1×2卷积核，采用最大池化方式；

(2)为提高网络学习能力，增加卷积核种类，第一层卷积层和第二层池化层由6 种增加为128 种，第三层卷积层和第四层池化层由16 种增加为256种，第五层全连接层由120种增加为512种；

(3)卷积过程中对特征图进行边界补零，保证特征图卷积前后的大小保持一致，便于进行分路卷积，加权融合操作。

如图8(b)和图8(c)所示，在改进CNN-5网的基础上，在第二层池化层和第三层卷积层之间，分别再加入1 至2 层卷积层作为比较，得到改进CNN-6 和改进CNN-7 网络。其中添加的卷积层卷积核大小为1×5，种类数量为256种。

将1.2 节中每类数据集的信号作为网络的输入x，将化爆样本标注为1(正类)，将地震样本标注为0(负类)，并进行one-hot 编码，作为真实值y_，将经过网络的输出值y作为预测值。网络训练的目的就是让训练集的预测值y的分布与真实值y_的分布尽可能保持一致，即y的分布与真实值y_的分布之间的差值尽量的小，可将二者差值定义为损失函数。本文采用交叉熵损失函数，并采用Adam 算法对网络模型进行基于梯度下降的优化，使得参数更加平稳。

此外，本文还采用了L2 规格化和50%的dropout 防止过拟合问题，使用滑动平均模型用于控制变量的更新幅度，使网络结构更稳定。最后使用softmax 作为分类器，完成化爆和地震的分类。

3 实验设计与结果分析

3.1 评价指标

如果神经网络输出的预测值y与真实值y_相同时，那么认为网络能够正确得识别出该类次声事件。通过比较神经网络输出的预测值y与真实值y_可以得到4 个统计量：Ture Positive (TP，真实值为1 且被网络预测为1)、False Positive (FP，真实值为0 但被网络预测为1)、False Negative (FN，真实值为1 但被网络预测为0)、Ture Negative (TN，真实值为0且被网络预测为0)。基于TP、FP、FN、TN四个统计量可以得到准确率、假阳性率和假阴性率和调和平均数4 个评价指标。利用以上4 个指标可以根据实验结果对网络准确性和稳定性进行较为可靠的分析。

3.1.1 准确率

准确率(Accuracy，ACC)表示所有样本被正确分类的比例，其公式表达为

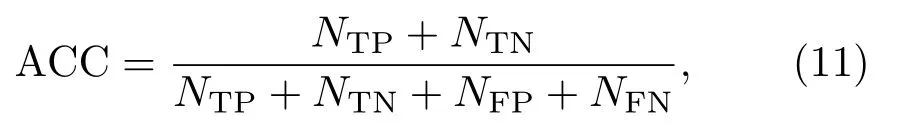
其中，NTP表示真实值为1 的样本被正确分类的数目，NTN表示真实值为0 的样本被正确分类的数目，NFP表示真实为0 的样本被错误分类的数目，NFN表示真实为1 的样本被错误分类的数目。ACC的取值范围为[0，1]，值越接近1，分类性能越好。

3.1.2 假阳性率

假阳性率(False positive rate，FPR)表示真实值为0 但被预测为1 的样本数量在所有真实值为0的样本中占的比例，其公式表达为FPR取值范围为[0，1]，值越接近0，分类性能越好。

3.1.3 假阴性率

假阴性率(False negative rate，FNR)表示真实值为1 但被预测为0 的样本数量在所有真实值为1的样本中占的比例，其公式表达为

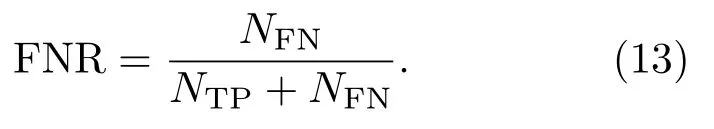
FNR取值范围为[0，1]，值越接近0，分类性能越好。

3.1.4 调和平均数

当存在极偏数据时，单独使用FPR 和FNR 很难对整体的分类性能进行客观评价，需要使用一个两者兼顾的指标。调和平均数(Harmonic average，HA)是假阳性率FPR 和假阴性率FNR 的兼顾指标，是1-FPR和1-FNR的平均数。HA值的性质是，只有当FPR和FNR 两者都非常低的时候，它们的HA 值才会高，如果其中之一很低，HA 值会被拉得接近于那个很低的数。其公式表达为

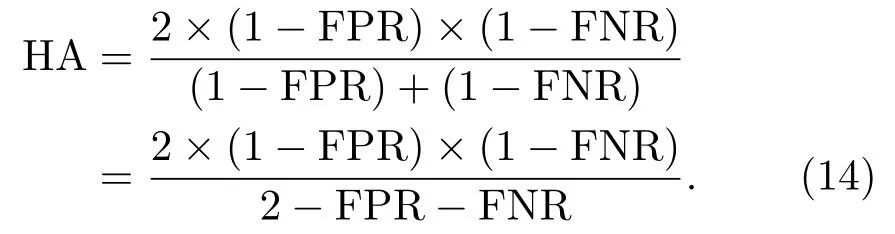
HA取值范围为[0，1]，值越接近1，分类性能越好。

3.2 实验设计

共设计两组对比实验，即相同输入和不同网络的对比实验以及相同网络和不同输入的对比实验。

3.2.1 相同输入和不同网络

将Welch 功率谱作为第一类对比实验的输入，BP 网络(隐藏层节点数分别为17、20、26)、一维LeNet-5网络和改进CNN，得到分类识别结果。

3.2.2 相同网络和不同输入

将原次声信号、Welch 功率谱、IMF 分量比和IMF 奇异谱熵分别作为网络输入，送入改进CNN中，得到分类识别结果。

3.2.3 实验平台和参数设置

本文使用的操作系统为Windows10，使用CUDA10.0 和cuDNN7.4 加速训练；使用NVIDIA Quadro P4000 (8G 内存)；使用网络开发框架为Tensorflow1.14；用python 进行编程；使用CPU为Intel(R)Core(TM)i7-8700 CPU@3.20 GHz 3.19 GHz。

每次分类实验共进行12000 次训练，每次从训练集中按照顺序抽取8 个样本输入网络进行训练，即batch_size 设置为8，训练集抽取完成一个批次(epoch)后对训练集进行一次打乱。若将训练集样本数定义为data_size，则每个批次可以表示为

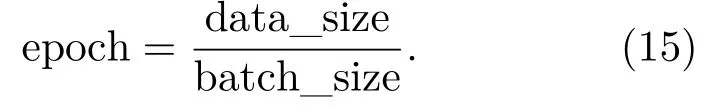
每训练100 次记录一次损失函数、训练准确率和测试准确率。训练和测试结束后分别计算验证集的准确率、假阳性率和假阴性率和调和平均数。

3.3 实验结果与分析

3.3.1 相同输入和不同网络的实验结果分析

七类不同网络的训练损失，训练和测试准确率如图9～10所示。

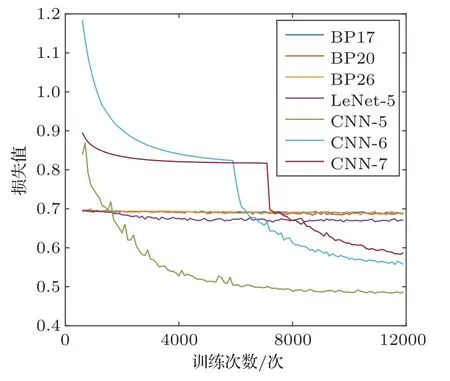
图9 七类不同网络结构的训练损失Fig.9 Seven different network structure training costs

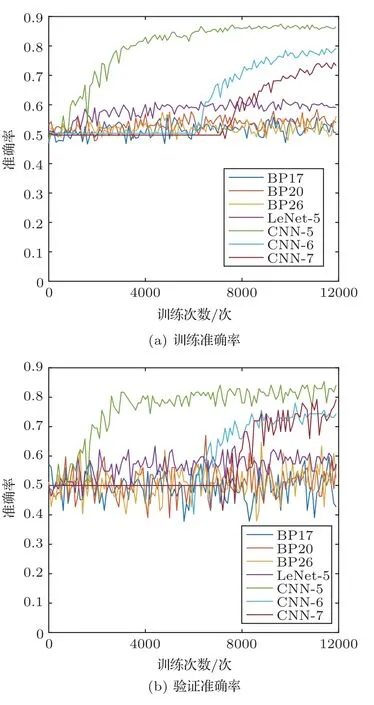
图10 七类不同网络结构的训练和验证准确率Fig.10 Seven different network structure training and testing accuracy

通过图9～10 可以看出，BP17、BP20 和BP26三个网络的训练损失值长时间保持在0.69～0.695之间，收敛趋势不明显，网络训练准确率和验证准确率都在40%～60%内上下浮动。由于此分类为二分类，所以准确率在50%以下不具有分类识别意义。由此可见，BP 网络无法对次声信号功率谱进行有效训练分类。

相比BP网络，一维LeNet-5网络的损失数值要更低，收敛性更强，训练准确率和验证准确率可以都能达到60%左右，比BP网络提高10%以上，可见LeNet-5 网络对次声信号功率谱可以进行一定的训练分类，但分类效果还有待加强。

在改进CNN 网络中，网络的训练损失都可以收敛到0.5～0.6 之间。训练准确率能够达到70%～85%。验证精度最高的是改进CNN-5 网络，能够达到80%，改进CNN-6 和改进CNN-7 都能达到75%以上，精度明显高于其他网络。

计算七类不同网络结构关于测试集四个评价指标，结果如表1所示。

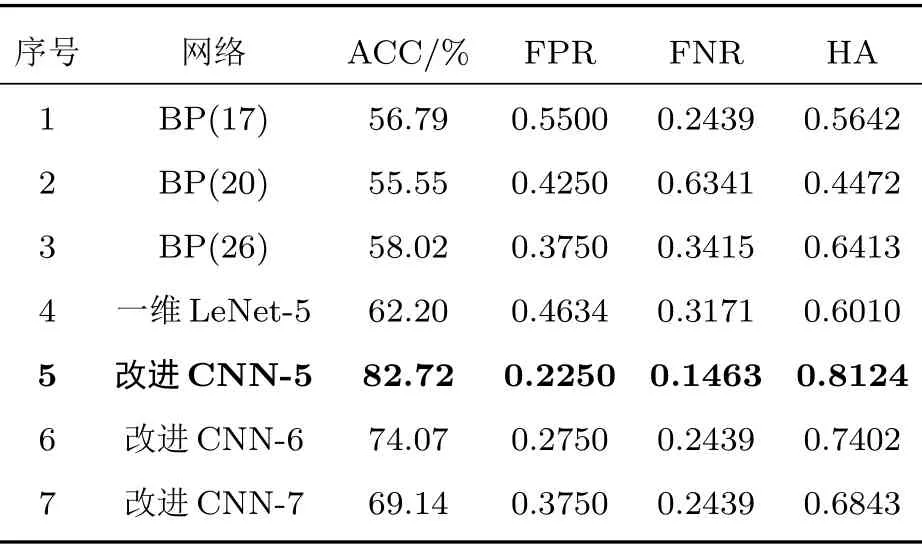
表1 七类不同网络结构的分类评价指标Table 1 Classification evaluation index of seven different network structures

表1中每个评价指标的最优值都以加粗的形式表示。从表1中可以看出，改进CNN-5 网络的四项评价指标均优于其他(ACC、HA 最高，FPR、FNR最低)。相比第二名改进CNN-6 网络，改进CNN-5网络测试准确率提升了8.67%，假阳性率降低了5%，假阴性率降低了9.76%，HA 值提升了7.22%。因此可以得出，改进CNN-5网络在七类网络中分类效果最显著。

为验证改进CNN-5 的稳定性，重复1.1 节中生成数据集的操作20 次，得到20 个不同的数据集，重复上述实验方法，得到七类网络的分类实验结果，如图11所示。

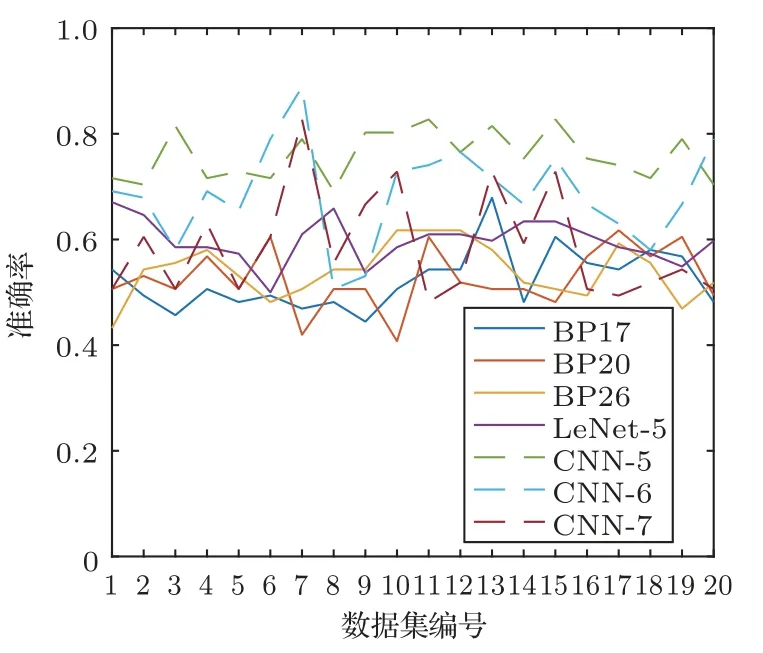
图11 二十组数据集的七种网络的分类结果Fig.11 The classification results of seven networks in twenty datasets

从图11中可以看出，改进CNN-5和改进CNN-6 网络分类精度明显优于其他网络，而改进CNN-5网络平均测试准确率比改进CNN-6 网络高7.28%，因此，改进CNN-5网络的分类效果相对更好。

3.3.2 相同网络和不同输入的实验结果分析

依次对原信号、Welch功率谱特征、IMF分量比特征[11]和IMF 奇异谱熵特征[12]进行归一化。四种不同输入特征的训练损失，训练和测试准确率如图12～13所示。

通过图12～13可以看出，原信号和IMF 分量比特征的训练损失最后保持在0.65 左右，训练精度都在65%左右，验证精度在60%以下，说明网络能够对两类特征进行一定程度的训练，但分类结果不够理想。但进行IMF 分量比特征提取后，损失函数收敛速度得到提高。

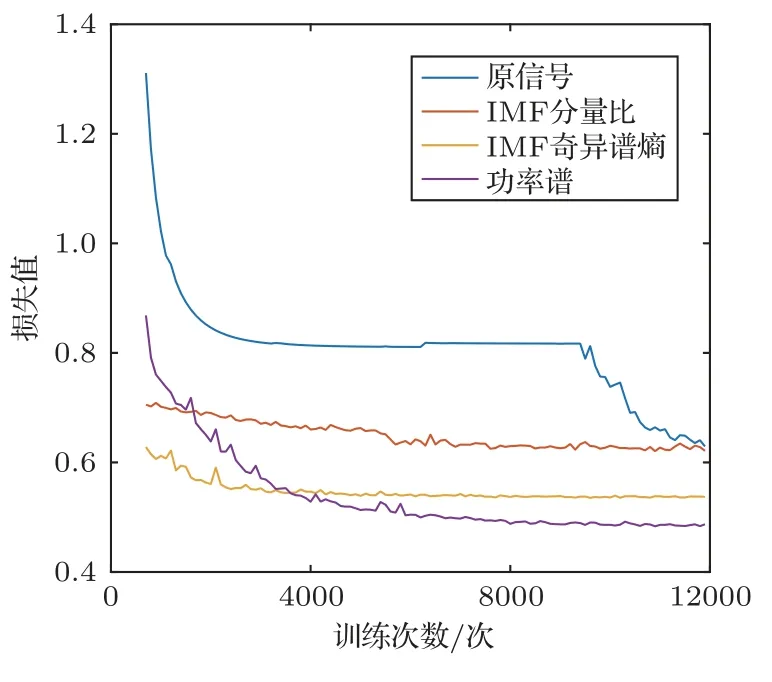
图12 四种不同输入特征的训练损失Fig.12 Four different network structure training costs

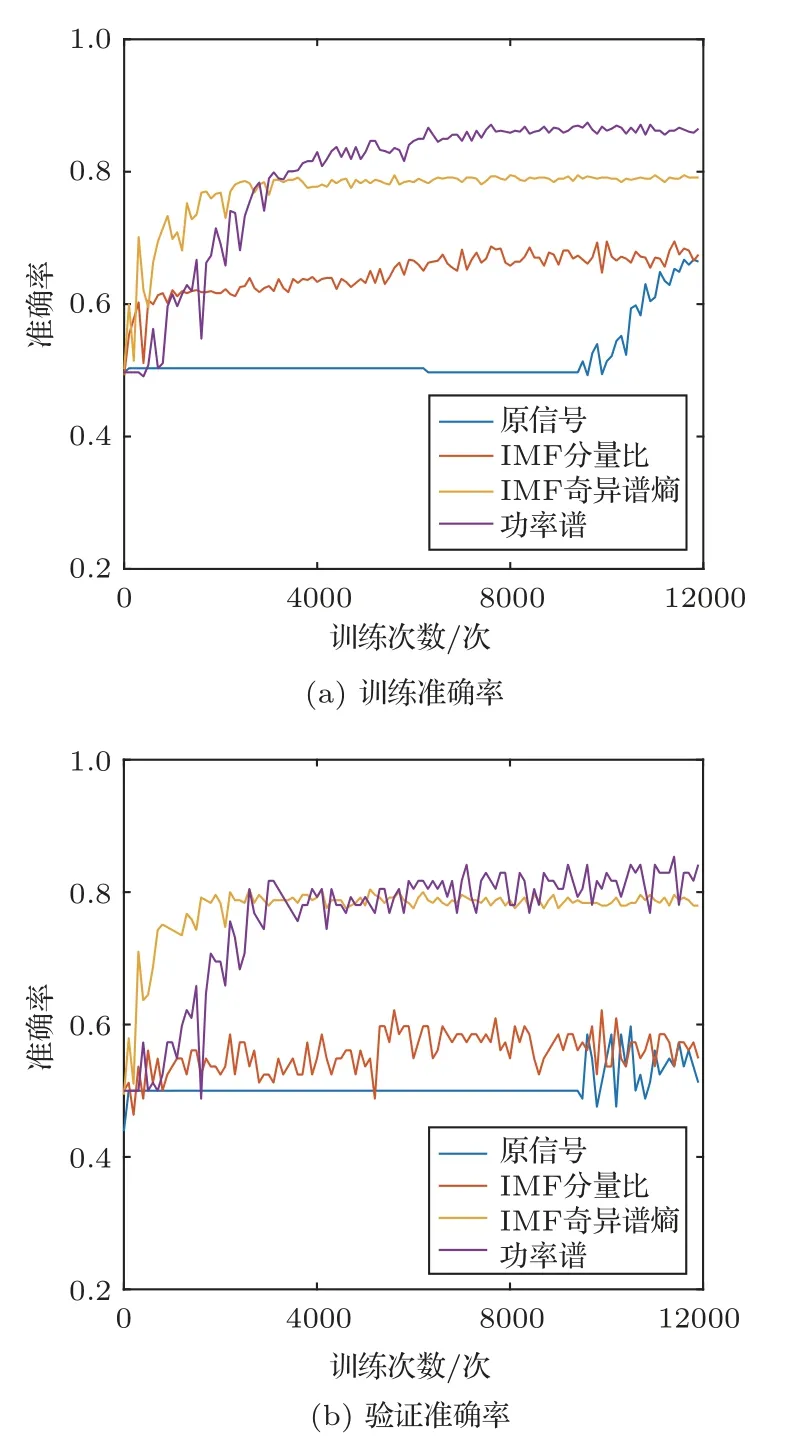
图13 四种不同输入特征的训练和验证准确率Fig.13 Four different network structure training and testing accuracy

相比IMF分量比，IMF 奇异谱熵的损失数值要更低，收敛更快，训练准确率和验证准确率可以分别达到79%和78%，比IMF分量比提高14%以上。

而使用功率谱特征作为网络输入时，训练损失都可以收敛到0.5 以下，为四种特征最优，训练准确率能够达到84%以上，验证准确率也能够保持在80%，精度要优于其他输入特征。综上所述，利用次声信号的功率谱特征作为神经网络的输入，得到的分类效果最好。

计算以上四种输入特征基于测试集的四个评价指标，结果如表2所示。

表2 四种不同输入特征的分类评价指标Table 2 Classified evaluation index of four different input characteristics

表2中每个评价指标的最优值都以加粗的形式表示。可以看出，Welch 功率谱特征的四项评价指标均优于其他特征(ACC、HA 最高，FPR、FNR 最低)。相比第二名IMF奇异谱熵，Welch 功率谱测试准确率提升了3.94%，假阳性率降低了4.33%，假阴性率降低了0.12%，HA 值提升了2.49%。因此可以得出，Welch功率谱特征作为输入时，分类识别测试精度最佳。值得注意的是，原信号测试准确率只能达到58%，进行功率谱特征提取后，测试准确率能够达到82%，上升了24%，说明进行功率谱提取是必要的。

为验证其稳定性，将3.3.1 节中得到20 个不同的数据集中的样本信号分别提取上述三种特征，重复上述实验方法，得到四类输入的实验结果，如图14所示。

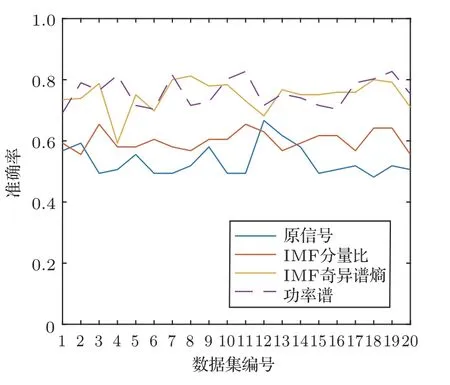
图14 二十组数据集的四种特征的分类结果Fig.14 The results of the classification of four features in twenty data sets

从图14 中可以看出，功率谱和IMF 奇异谱熵的分类精度明显优于IMF 分量比和原信号，而功率谱的平均准确率比IMF 奇异谱熵高0.96%。因此，采用功率谱作为网络输入的分类效果相对更好。

4 结论

本文通过建立CNN 模型和数据集完成模型训练，实现化爆和地震的次声事件的分类识别。实验证明CNN 的复杂特征提取能力能够简化传统方法特征提取过程，同时能够提高分类识别结果。

自然界中次声源种类繁多，次声事件不局限于化学爆炸和天然地震两种。深度学习具有处理多分类问题的优势，要实现多类次声事件的分类识别，需要建立一个不同类型(核爆、天然地震、化学爆炸、矿山爆炸、火箭发射等)的数据库。下一步工作中，将搜集更多类型的次声事件数据，并探究适宜次声数据的数据增强方法，选用更适合多分类的神经网络模型进行训练，完成多类次声事件的分类识别工作。