半波长管传声损失分析*

王 恒 毛崎波 胡龙轩 王渊德 谢 冉

(南昌航空大学飞行器工程学院 南昌 330063)

0 引言

利用声波叠加干涉原理的干涉管，因其简单的结构和优秀的消声性能在噪声控制领域中备受关注，例如著名的1/4 波长管和Herschel-Quincke(HQ)管。1/4 波长管利用管口入射声波在管端反射后，形成频率相同的声波发生叠加干涉作用[1]。1/4 波长管因其简单的结构和良好的消声性能，为许多工程领域提供了理想的解决方案，例如：在航空降噪领域，Oschwald等[2]利用1/4波长管干涉特性解决航空发动机的燃烧不稳定问题，通过实验证明加入1/4 波管后，燃烧室固有频率发生改变，提高燃烧的稳定性；在汽车降噪领域，刘涛等[3]将1/4 波长管运用在增压发动机进气系统，有效解决涡轮增压器的气流啸叫噪声。HQ 管利用两个分支管路径的不同改变了声波的相位[4]，声波叠加干涉从而达到降噪的效果。HQ 这种结构具有很大的可改造性，使得其在降噪领域具有很大发展潜力，为此出现了大量基于HQ 管的研究。早期，Selamet等[5]提出一种改进的多分支管并联模型，并且推导出传声损失理论模型；Desantes 等[6]在传统HQ 管两分支管中引入一根连接管，给出一种推导这种带有连接管理论模型的方法。随后，Torregrosa 等[7]改变了分支管横截面积，设计了一种横截面积渐变的HQ 管，以此来提高传统HQ 管的消声性能；Poirier 等[8]提出了一种HQ 管与声衬的组合模型，这种组合模型可以充分发挥二者的特性，达到更进一步的消声效果。在近期，Kim 等[9]设计了一种利用周期阵列的谐振管阻滞振速传播进而形成相位差的虚拟HQ 管，并且通过改变谐振管的排布方式实现降噪频率的可调节；Arjunan[10]利用3D 打印技术数字化打印特点，实现了HQ管数字化制造，使得HQ 管可以在指定频率降噪。除了上述理论实验研究，在工程应用中也可以看到HQ 管的身影，例如：Hallez[11]就将传统HQ 管应用在航空发动机进口降噪，在实际的测试中表明在特定频率下具有明显的降噪效果；Zhu 等[12]采用半主动控制HQ管对发动机的排气噪声进行控制，测试结果表明在50～150 Hz频率的范围内可以平均降噪35 dB。

以上论述中表明，无论在理论还是在实际工程应用中，1/4波长管与HQ管都表现出良好的消声效果，又因为二者具有相似的声学性能，为此本文提出了一种基于这两种干涉管的新的半波长管，如图1所示，其两端开口和传统半波长管相同[13]，但其另一端并不敞口而是连接主管类似于HQ 管，且其两端口位于同一主管横截面积上，使得相干波在同一主管横截面相遇，从而达到干涉降噪的效果，这又与1/4 波长管相似，这种结构布局方式使得这种新的干涉管占用空间更小，而且具有与1/4波长管和HQ管类似的消声性能。本文首先推导出半波长管传声损失理论模型，然后基于理论模型探究了传声损失的影响因素，根据各影响因素对宽频带传声损失模型进行了计算分析并且得出了较好的宽频带降噪效果，最后对理论模型进行实验验证和管端部修正，验证理论模型的可靠性。

图1 一种新型半波长管Fig.1 A new resonance tube

1 传声损失计算模型

图2是本文提出的半波长管的多分支干涉管理论模型示意图。图中各分支管管径均匀且串联排布，同时假设管中无流且声波以平面波传播。

对于图2所示的整个复杂的管道系统，由n个虚框中的基本子系统组成，就其中任意一个基本子系统而言，其进出口间的声压p和体积速度v可以表示为

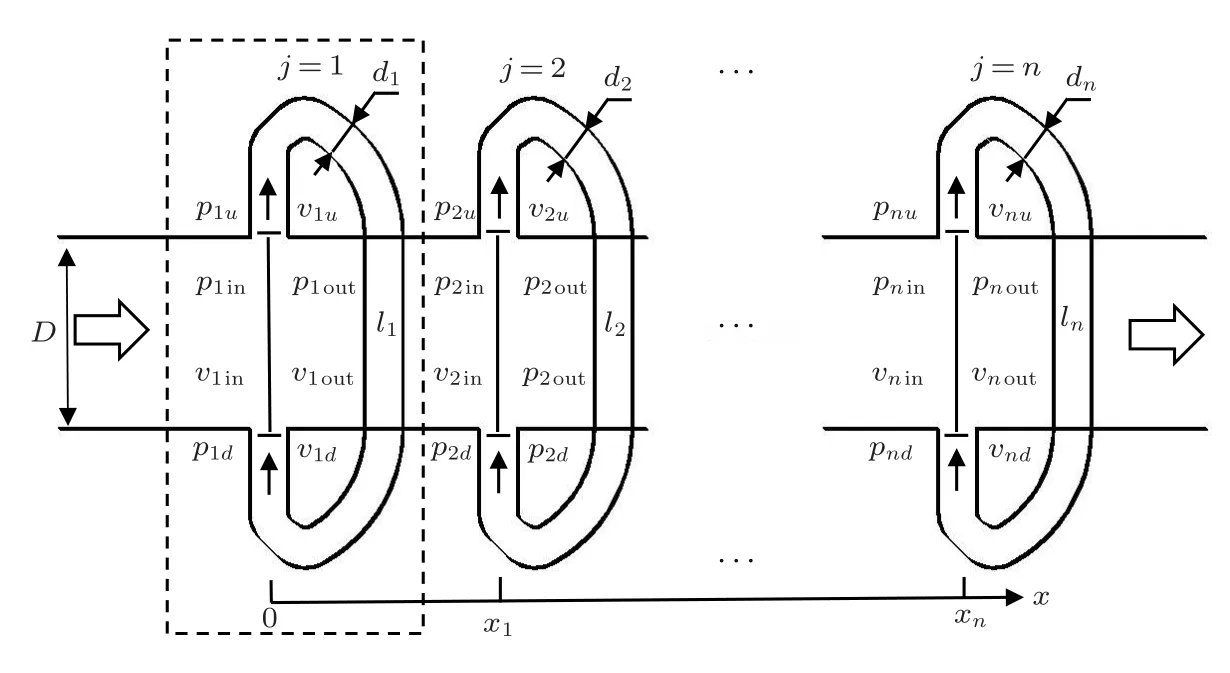
图2 串联排布的半波长管示意图Fig.2 Schematic diagram of half wavelength tube in series arrangement

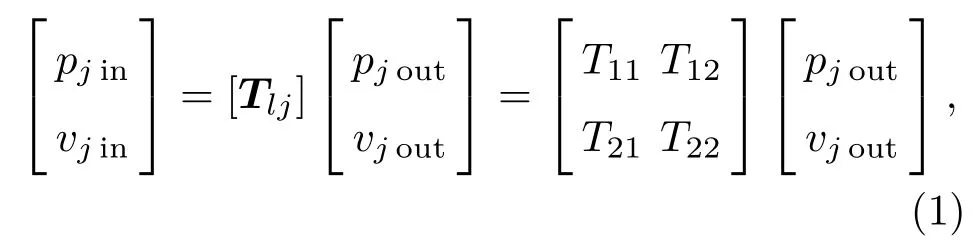
式(1)中，下标“j”代表第j个子系统，[Tlj]为该子系统中的传递矩阵，其中的4 个元素T11、T12、T21和T22称为四极参数[14]。同时，对于该子系统中的分支管的两端的声压p和体积速度v可以表示为

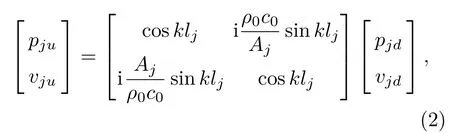
式(2)中，k=ω/c0为波数，ω为角频率，ρ0和c0分别为空气密度与声速，Aj和lj为第j个子系统中分支管的面积与管长，下标“ju”和“jd”分别为第j个子系统中分支管的上游与下游端口。

在上述的子系统中，在主管与分支管的连接处，即分支管的上下游端口，由压力和体积速度连续条件可得

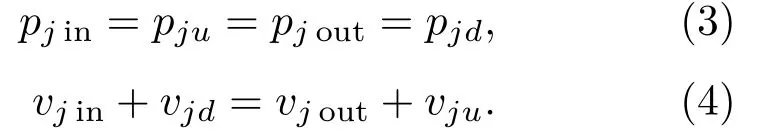
从式(2)和式(3)可得

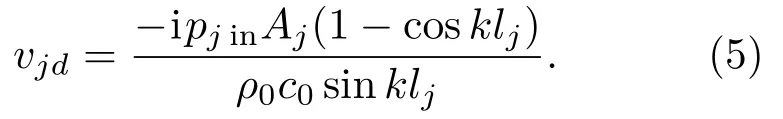
将式(5)和式(1)代入式(2)可得

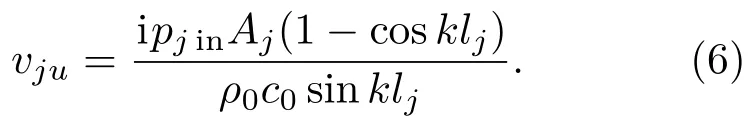
由式(1)～式(6)可得传递矩阵[Tlj]的所有四极参数的表达式，即

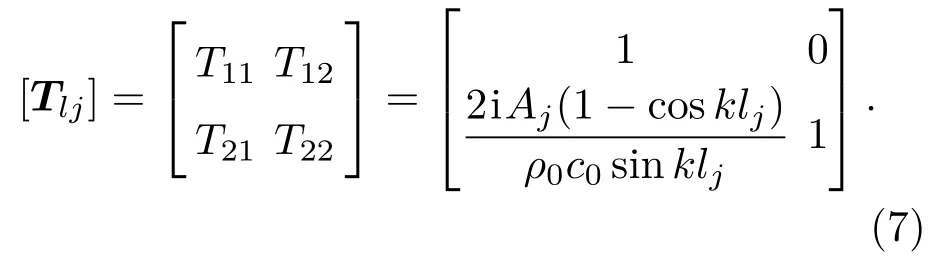
对于图2任意第j个子系统的进出口状态变量的传递关系可以通过式(7)表示，为了进一步得到整体管道系统的传声损失，只需要将各个子系统串联，则任意第j个子系统与第(j+1)个子系统间状态变量的传递关系可以表示为

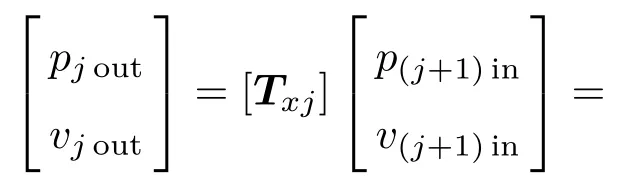
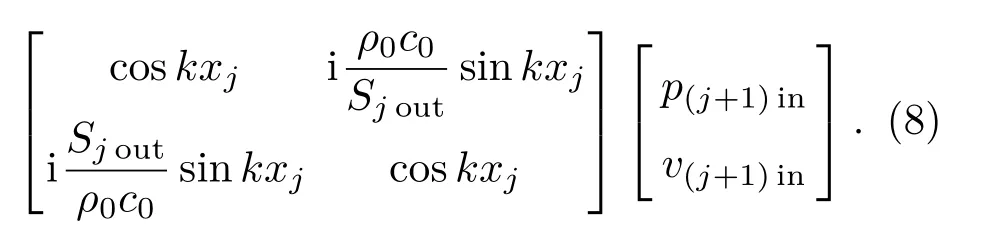
图2所示的整体管道系统由n个子系统通过相应的主管连接组合而成，为此可以通过如下传递关系式将整个系统进出口的声压p和体积速度v可以表示为

式(9)中，[T]为整个系统总传递矩阵，A、B、C和D为总传递矩阵的四极参数，[Tl1]、[Tl2] 和[Tln]为子系统传递矩阵([Tlj]，其中j= 1，2，···，n)，[Tx1]、[Tx2]和[Tx(n-1)]为对应的相邻子系统间的传递矩阵([Txj]，其中j= 1，2，···，n-1)。从而整个系统的传声损失表达式可以由四级参数定义为[14]

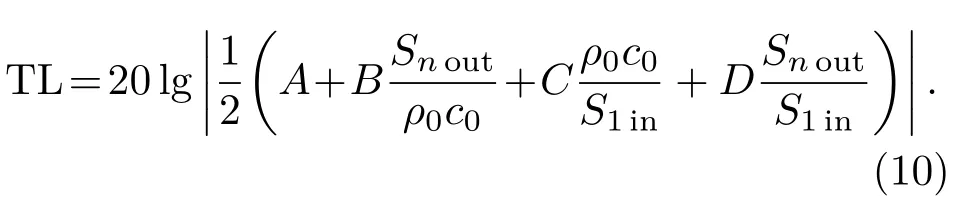
当已知分支管管数量和参数时，通过上述推导过程，可以得到四极参数A、B、C和D，将所得四极参数代入式(10)可以得出任意数量分支管串联模型的传声损失。

假设只有一个半波长管时，传声损失表达式为[14]

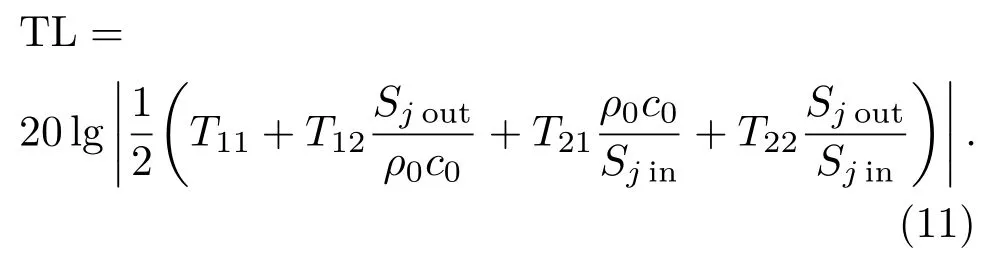
当Sjin=Sjout时，将传递矩阵[Tlj] 中四极参数代入式(11)可得

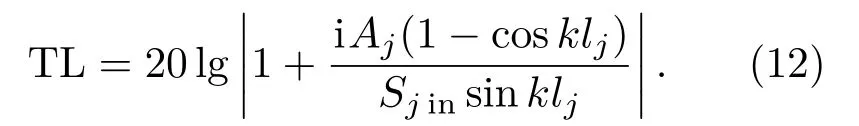
当进口端主管与出口端主管横截面积相等时，即Sjin=Sjout时，可知该子系统产生共振的条件为

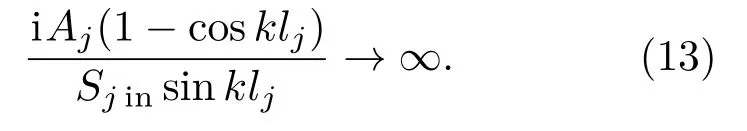
由此得到

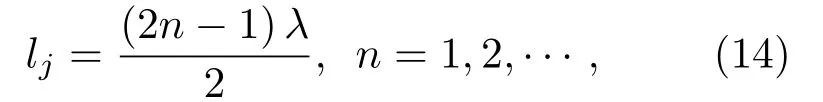
其中，λ为波长。由式(14)可知，当分支管长为半波长的奇数倍时产生共振，所以称之为半波长管，其共振频率为

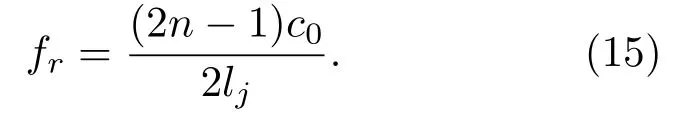
当xj=0时，简化为同一位置的多分支1/2管模型。

因为xj= 0，所以式(9)中，子系统之间的传递矩阵，将其和式(7)代入式(9)可得

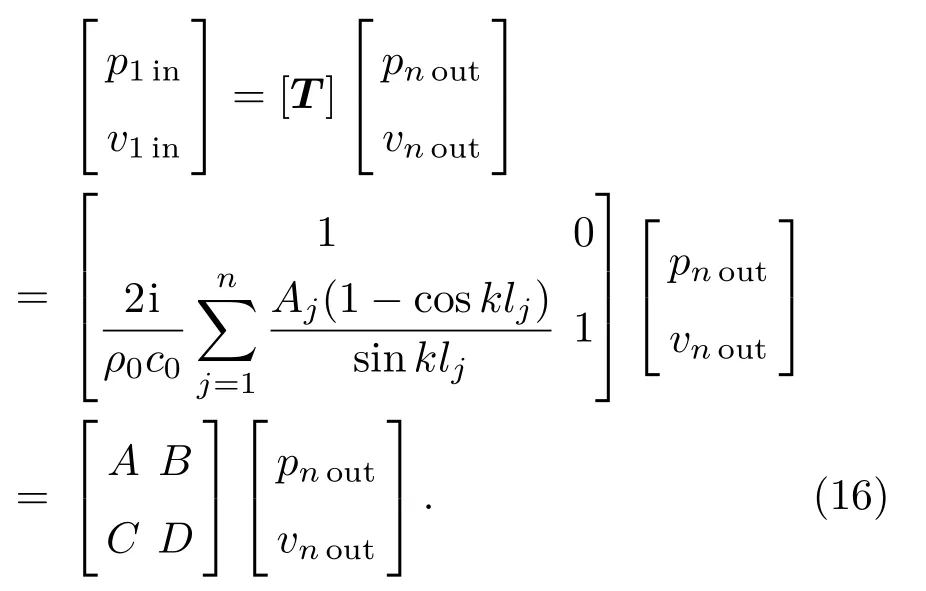
当进出口主管横截面积相等时(Sin=Sout)，将式(16)中四极参数值代入式(11)可以得到任意数量分支管同一位置时的传声损失为

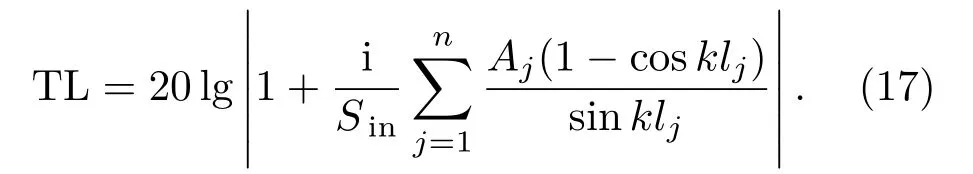
2 数值计算

在上述的理论模型中，推导出了半波长管的传声损失理论模型，但在多分支管模型时，式(9)和式(17)将会变得极其复杂，难以推导出对传声损失的影响因素。为了更直观探究出串联与并联模型中对传声损失的影响因素，下面基于前文推导的理论模型，进行了半波长管模型在不同管径和管长下以及在不同分支管距离下的传声损失数值计算，并将数值计算的结果统一表示为0～1500 Hz 上的传声损失曲线。

2.1 管径和管数对传声损失的影响

分析不同管径和管数在半波长管模型x=0 m(并联)时和x=0.1 m (串联)时对传声损失的影响，假设主管管径D=0.1 m，分支管管长l=0.5 m，并且各分支管长度相同。

首先，三分支管模型，图3表示管径变化时的传声损失。通过对图3(a)观察分析可知，x= 0 m 时，即同一位置多分支管时，增加分支管管径，即增加分支管总横截面积可以增加传声损失，拓宽固有频率处的消声峰，增加其消声性能。通过对图3(b)观察分析可知，x=0.1 m时，多分支管串联时，增加分支管管径，同样可以增加传声损失。

其次，分支管的横截面积之和保持不变，而改变分支管数目，结果如图4所示。对图4(a)结果分析可知，x=0 m时，不管每个模型中分支管数量是否相同，只要总的分支管横截面积相同，传声损失也相同。对图4(b)结果分析可知，x= 0.1 m 时，与x=0 m时类似，传声损失基本保持不变。

最后，对比图3、图4中x= 0 m 和x= 0.1 m可以发现：在分支管长不变的情况下，无论是串联还是并联模型，改变管径和管数都不会改变模型的固有频率，这与理论模型相一致，由式(16)可知，并联模型的共振频率的条件为sinklj= 0∪(1-cosklj)≠ 0，由共振条件推得共振时的条件与式(14)相同，共振频率也与式(15)相同；在管径和管数相同的情况下，串联模型与并联模型的传声损失基本相同。

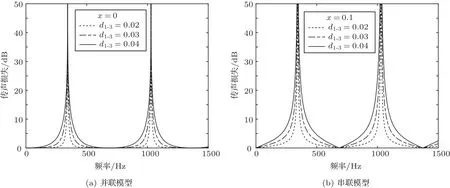
图3 两种模型不同管径传声损失Fig.3 Sound transmission loss of the two models with different pipe diameters

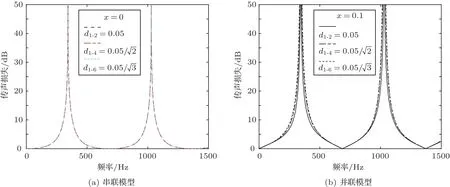
图4 两种模型不同管数传声损失Fig.4 Sound transmission loss of the two models with different number of the tube

2.2 管长对传声损失的影响

探究管长对半波长管传声损失的影响，同样主管横截面积不变(主管管径D= 0.1 m)，分支管管径保持不变。从2.1 节管径对传声损失影响的结果可知，当主管管径已知，分支管管径的增加可以拓宽消声频率，因此为了获得更好的消声效果，所以选择分支管管径为d= 0.05 m，支管间的距离为x=0 m或者x=0.1 m。

为了更清楚展示出管径改变的计算结果，选择10 分支管模型进行计算，并通过式(15)计算相应的固有频率，各分支管的长度和固有频率如表1所示。

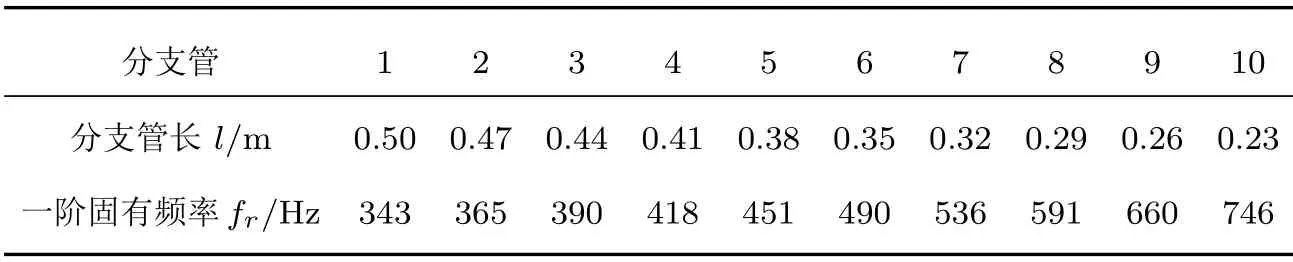
表1 10 分支管模型物理尺寸Table 1 Physical dimensions of 10 branch tube model

由理论模型可知，无论是串联模型还是并联模型，固有频率都是由分支管的长度决定的，所以将串联和并联模型在不同管长下的传声损失计算结果进行对比，计算结果如图5所示。

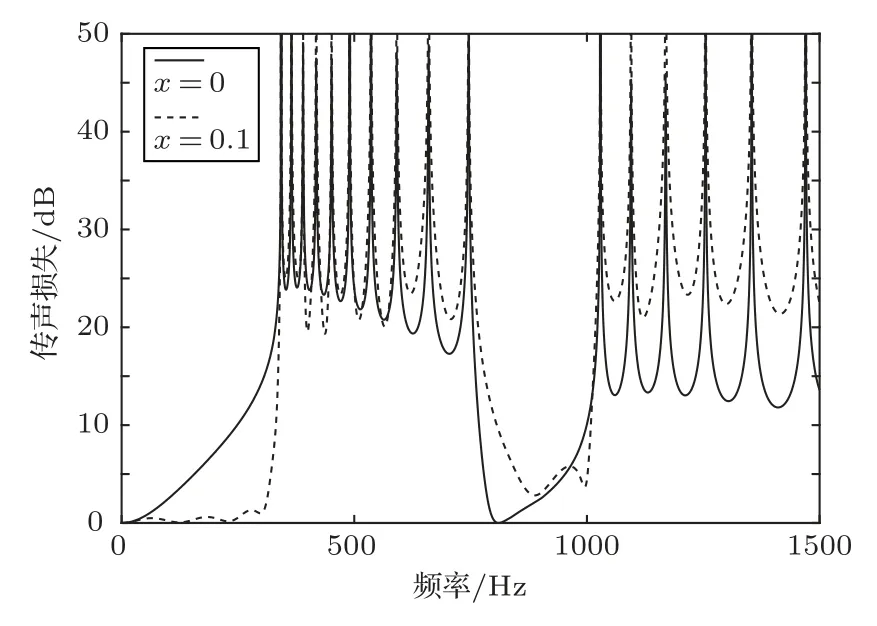
图5 串并联模型不同管长传声损失计算结果Fig.5 Calculation results of sound transmission loss of different tubes in series and parallel models

在图5所示的计算结果中可以看出，分支管管距为零与不为零的相同之处在于都产生了共同消声尖峰，这与之前的理论模型相符合，由于两种模型的物理尺寸相同，所以二者具有相同的共振峰；从两者的传声曲线可以看出，当各分支管之间的长度差适当，即各分支管之间固有频率差一定，都可以形成宽频带传声损失。差异在于从形成的频带可以看出，一阶消声频带二者差距不大，但是在二阶消声频带，串联的传声损失要明显高于并联。

2.3 分支管之间的距离对传声损失的影响

本节计算所用的10 分支管模型与表1相同，探究分支管之间距离对传声损失的影响，分别取x等于0.001 m、0.01 m、0.1 m、0.2 m 和0.3 m，计算结果如图6所示。

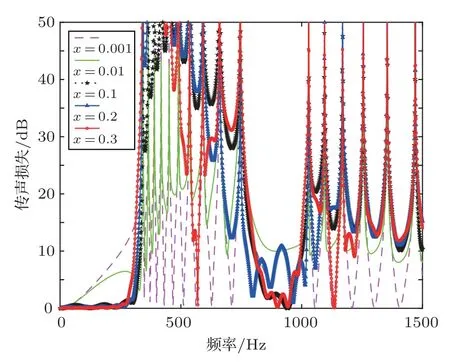
图6 不同分支管管距对传声损失的影响Fig.6 Influence of different branch tube spacing on sound transmission loss

从图6中可以看出当分支管之间的距离较小(x= 0.001 m)时，基本不会形成频带消声效果；随着距离的增加，宽频带的消声效果开始出现，并且频带的消声量级也在增加，同时也可以看出随着距离的增加，宽频带的稳定性在降低；当x=0.3 m时，频带会出现剧烈的波动，频带也随之变窄。综合对比可以看出在x=0.1 m时宽频带的消声效果较好。

2.4 宽频带传声损失尺寸设计

在以上管径、管长以及支管管距对传声损失影响的系统的探究中，应用数值计算的方法，得出了本文所提出的半波长管的各种影响因素对其传声损失作用规律，将在此基础上，进一步对宽频带传声损失进行尺寸设计。

降噪频带设定为350～1350 Hz，要求频带内不低于20 dB的消声量级。基于理论模型通过数值计算软件中的fmincon 函数进行优化计算，得到宽频带传声损失的管长尺寸如表2所示，结果如图7所示。

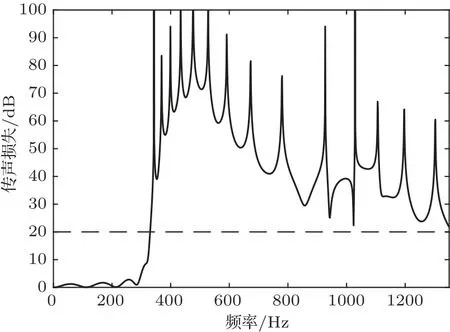
图7 宽屏带传声损失Fig.7 Broadband sound transmission loss

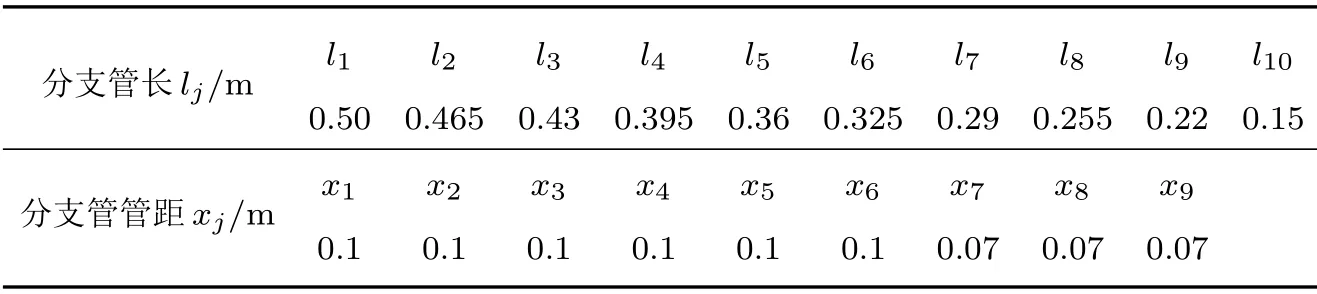
表2 宽频带传声损失模型尺寸Table 2 Dimensions of broadband transmission loss model

由图7可知，利用本文所推导理论模型和数值计算结果，对半波长管尺寸设计，可以实现精确的宽频带传声损失控制，从而达到目标要求。

3 实验验证和端部修正

为了对理论结果进行验证以及对管端部在非平面波引起的误差进行修正，对理论模型进行了实验验证并且采用实验的方法进行端部修正。

首先，搭建实验装置，然后采用四传感器的传递函数法对不同管长单分支管模型的固有频率进行了测量，主管和分支管尺寸如表3所示，其实验装置如图8所示。

图8 实验测量装置Fig.8 Experimental measuring device

其次，采用实验的方法对理论模型中管端部进行修正[15]。单分支管时，分别测量了5 根不同长度分支管的传声损失，其中各管尺寸如表3所示，结果如图9所示，基于传声损失的实验数据得到各管的固有频率。将理论值对照实验所得固有频率进行修正得出端部修正系数Δl= 3.75r(r为分支管半径)，修正后固有频率计算公式(式(15))变为，修正后的理论与实验结果对比如图10所示。

表3 主管与分支管尺寸Table 3 Dimensions of main and branch tube

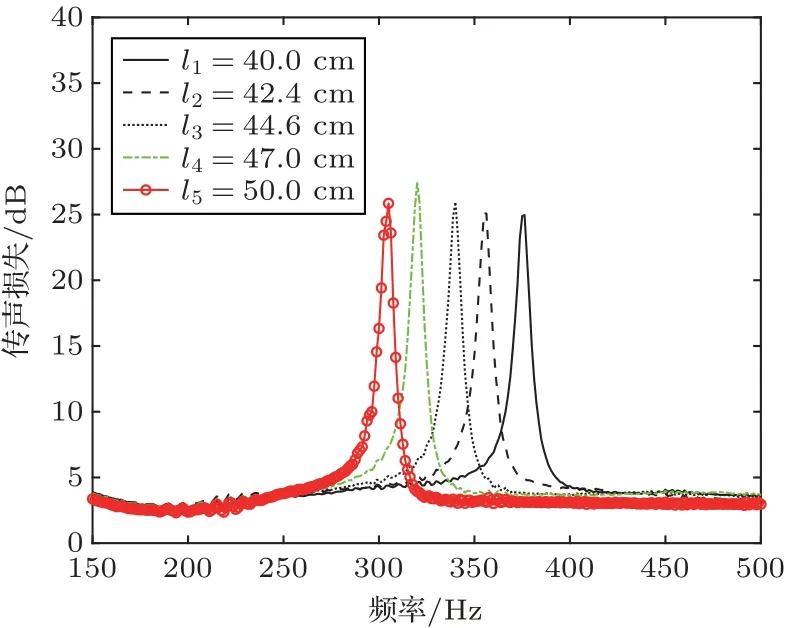
图9 不同管长传声损失Fig.9 Transmission loss of tubes of different lengths

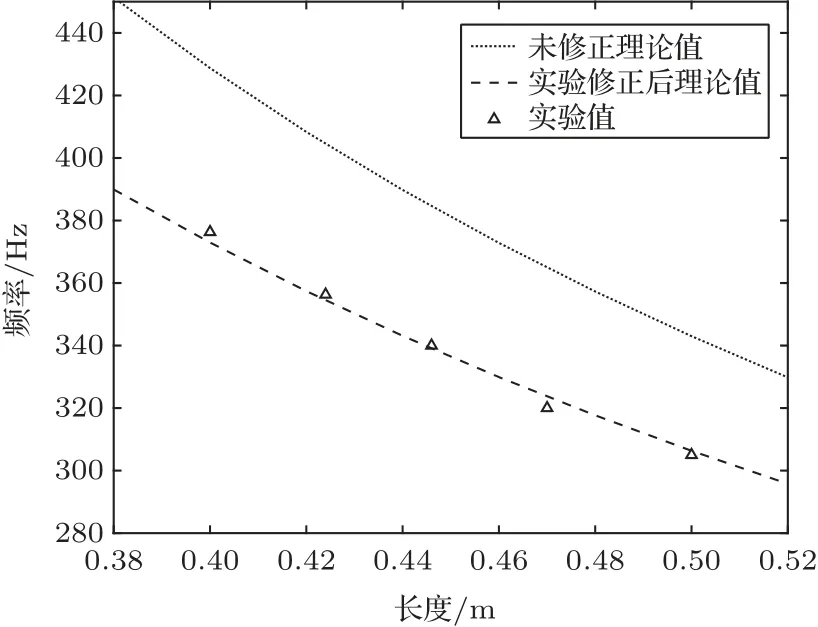
图10 分支管端部修正结果Fig.10 The end correction result of branch pipe

最后，引入端部修正后对传声损失理论模型进行验证。当管长同为0.5 m 时，分别对单分支管、双分支管和三分支管的传声损失进行测量，其中双分支管与三分支管管距为0.06 m，分支管与主管其余具体尺寸如表3所示，对比实验测得的结果对修正后的理论结果进行验证，如图11所示。

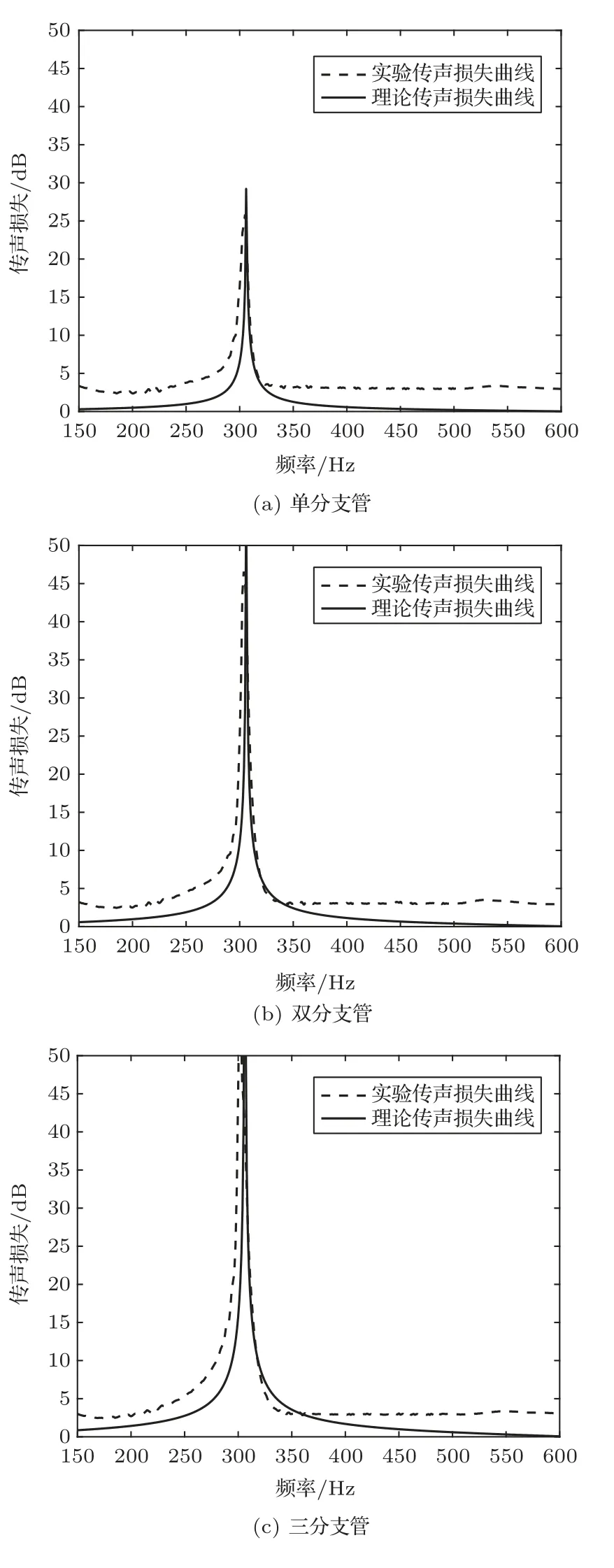
图11 不同分支管数理论与试验对比Fig.11 Comparison of theory and experiment with different branch number

4 结论

本文首先提出一种新的半波长管模型，并推导出任意分支管理论模型；然后通过数值计算分析了传声损失影响因数，根据影响因数分析的结果以及数值计算软件计算结果设计了宽频带传声损失的模型尺寸，得出350～1350 Hz 且不低于20 dB 的宽频带消声效果，证明本文所提出的半波长管具有良好的消声潜力；最后通过实验方法对理论模型进行修正和验证，修正理论模型的同时也证实理论本文所推导理论模型的可靠性。未来的研究中可以将其设计为一种空间折叠结构声学超材料，使得其具有完美吸声效果以及亚波长厚度[16-17]，使得在各领域应用中具有更大的潜力。