多层多孔吸声材料结构参数优化设计*

吴 量 刘 淼 刘学文 熊鑫忠 庞金祥 张和伟

(1 上海工程技术大学机械与汽车工程学院 上海 201620)

(2 上海普信科技有限公司 上海 200050)

0 引言

多孔吸声材料目前被广泛应用于汽车、高铁和飞机的内饰以及建筑内装材料中，以降低噪声的影响。多孔吸声材料的实际应用大多采用复合式结构，声波在进入多层结构中逐层递减，可以实现较好的吸声效果[1]。关于提高复合结构吸声性能方面的研究，研究人员多采用实验法优化和等效流体模型仿真优化。经大量研究表明，设置梯度结构有利于提高复合多孔吸声材料的吸声性能。Zhu等[2]研究了由不同孔隙结构组成的双层和3 层梯度结构的吸声性能，发现3 层梯度吸声结构性能最优。Wang等[3]通过对多孔金属纤维材料的吸声梯度结构研究，发现层间边界条件对吸声性能的影响较大，得到不同孔隙的梯度结构虽然只有2～3 mm，但吸声性能明显优于同样厚度的单层材料。以上研究表明多孔复合材料的结构是影响材料吸声性能的重要因素，通过结构优化的方式可以提高材料的吸声性能。

现有优化研究的理论模型多是基于Biot 理论、等效流体模型(Johnson-Champoux-Allard (JCA)、Johnson-Allard (JA))和传递矩阵法(Transfer matrix method，TMM)等，如Wang 等[4]基于Biot理论与TMM 建立吸声模型，研究了多孔材料和弹性板组合的双层复合结构流阻、孔隙率和压缩率对结构吸声的影响。杨晓涛等[5]基于统计能量分析模型建立了Kriging 近似模型，并对其进行多目标优化，得到了满足厚度要求的最优结构参数，同时降低了结构重量、价格和性价比。Shen等[6]采用布谷鸟搜索算法，基于JCA 和TMM 对压缩式多孔金属材料的结构参数进行优化，得到了在100～6000 Hz 范围内吸声系数均值为0.5105 的4 层最优结构。张姮李子等[7]采用释压法研究了吸声结构的吸声性能和多孔材料参数之间的关系，并根据释压法与材料厚度敏感的特性优化了结构厚度参数。Yang 等[8]为了实现在2000～5000 Hz 之间吸声系数大于70%的效果，以单层多孔金属铜材料和带有空腔的结构为对象、结构厚度为变量、吸声系数为目标进行优化计算，采用分组实验测试的方法实现了优化目标。Chen 等[9]使用灰度分析法和多目标粒子群算法对材料合成物进行量优化，提升了聚氨酯发泡材料的声学性能。刘新金等[10]采用JA模型与阻抗传递理论建立了双层复合结构吸声模型，研究了多孔材料背靠刚性壁和空气层的吸声性能参数影响。但是JCA 和JA 模型都是等效流体模型，不考虑多孔材料骨架和流体的耦合作用，且在低频的表现欠佳，需要做一些参数的修正。综上所述，已有的研究局限于利用等效流体模型、实验测试或是其他统计能量模型建立的理论模型研究多层结构吸声性能，却忽略了Biot理论分析骨架和流体部分的耦合作用。

本文以Johnson-Champoux-Allard-Lafarge(JCAL)为理论模型[11-12]求解多孔材料流体部分的参数，利用Biot 理论模型计算骨架与流体的耦合部分、TMM用于计算多层结构间声波的传递。相较于JCA 等流体等效模型，JCAL模型修正了声波复数密度和体积模量在低频吸声的结果；Biot 模型考虑到了声波在流体部分和骨架部分的耗散；在TMM 方法中引入传递矩阵的修正因子，提高了多层多孔材料仿真的准确性。文章研究过程如下：首先，基于上述理论建立了多层结构吸声系数计算模型，并利用阻抗管验证了模型的准确性；继而以3 层多孔结构为研究对象，优化其结构参数使得结构整体厚度由10.8 cm 降为9 cm，同时维持了吸声性能、减轻了结构重量；最后利用阻抗管验证了优化结构的准确性。文章详细分析了优化前后吸声结构在吸声能力、厚度和质量方面的变化，以及3层结构材料排列顺序的影响。

1 多层弹性介质中的声传播理论模型

为了求解多层多孔材料吸声系数结果，本文提出JCAL 和Biot 理论模型与TMM 结合，建立多层多孔吸声材料理论模型。具体表现为JCAL 模型对单层多孔材料求解修正后的动态密度和动态体积模量；将结果带入Biot 理论和TMM[13]得到声波复波数，进而求得多层结构的吸声系数。文章所用的边界条件与白聪等[14]相似，都是基于背衬刚性壁面。

根据JCAL模型求解修正后的体积模量和动态密度。表达式[10-11]分别如下：

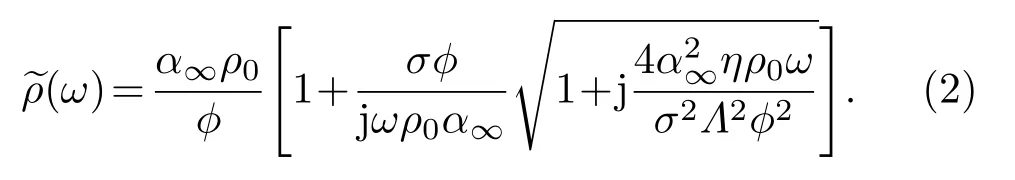
以上公式所需参数分别为开孔孔隙率φ、静态空气流阻σ、弯曲度α∞和黏性特征长度Λ、热特征长度Λ′和静态热导率k′0，均由实验测试或逆推得到。

假设有一束声波以垂直入射的方式进入到多孔材料中，根据Biot 理论会存在两种波在结构中传播，分别是流体中的纵波和骨架中的纵波，两种纵波的复波数δ1和δ2的表达式为

其中，Δ由公式(5)给出：

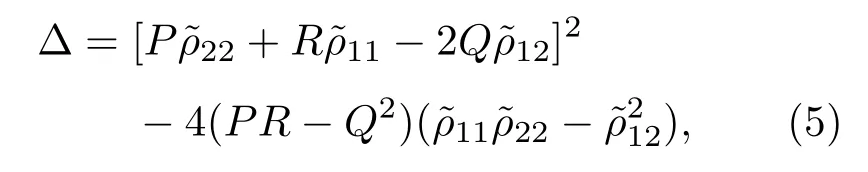
根据上述的波动方程公式(3)和公式(4)，单层结构的多孔材料的表面阻抗Z为

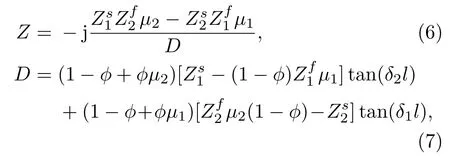
其中，Zif是第i层材料中其流体部分的特征阻抗，Zsi是固相部分的特征阻抗；μi(i= 1，2)表示多孔材料中两种纵波的空气与框架传播速度的比值。

根据表面阻抗的计算公式(6)，可以求出材料的声学特性参数反射系数R和吸声系数α，具体表达如下：

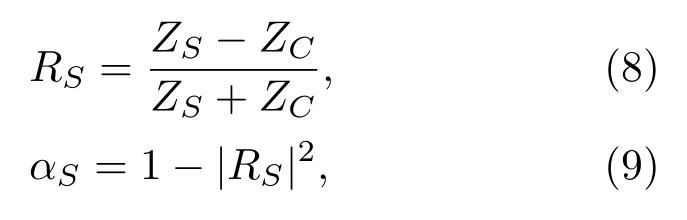
其中，ZS是材料的表面阻抗，ZC是相邻层的特征阻抗。本文研究的是背靠刚性墙的吸声结构，因此ZC表示墙面的特征阻抗。

TMM 表示层与层之间阻抗的传递关系，需根据以下关系式推导多层结构理论模型，首先双层材料界面M1和M2处矩阵关系为

其中，T为传递矩阵，V(Mi)(i= 1，2)表示每层材料的状态量。

在多层多孔材料中，多层结构的全域传递矩阵的表达式如下：

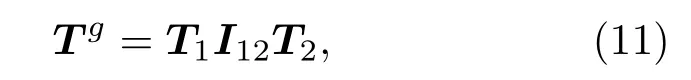
其中，T1和T2表示每层材料的状态矩阵，本文中多层材料结合的分界面属材料拼合，并未使用胶粘，故使用修正因子I12能更好地表征多层结构间分层界面的物理描述，具体公式如下表示：

根据以上结论推导得到多层材料的传递矩阵求解相关参数的表达式如下：

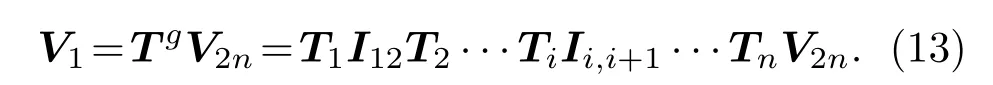
综上所述，计算多层结构吸声系数需要开孔孔隙率φ、静态空气流阻σ、弯曲度α∞和黏性特征长度Λ、热特征长度Λ′和静态热导率k′0，以及Biot 理论中所需的材料密度ρ、杨氏模量E、泊松比ν和阻尼损耗因子η。

2 实验材料测试与样品制备方法

2.1 材料参数测试与逆算

本文选用了两种不同参数性质的开孔聚氨酯发泡材料和一种吸声棉作为3 层结构的研究对象。其中在厚度参数优化过程中，吸声棉的厚度保持不变，只优化两种聚氨酯发泡材料的厚度。模型中参数通过实验测量或者逆推计算得到，其中黏性特征长度、热特征长度、弯曲度和静态热导率由遗传算法逆推得到；孔隙率、材料密度通过开孔孔隙率＆密度仪PHI[15]设备测量，流阻通过流阻仪SIGMA[16]测得；物理参数即杨氏模量、泊松比、阻尼损耗因子通过准静态力学分析仪QMA[17]测量得到。具体参数如表1所示。为了方便说明，聚氨酯发泡材料记为A和B，吸声棉记为C。

表1 材料参数Table 1 Material parameters

关于材料参数黏性特征长度、热特征长度、弯曲度和静态热导率的逆推，本文采用了遗传算法辨识参数的方法，具体原理如图1所示。

如图1所示，整个过程分为4 个模块，在遗传算法逆推流程中以图1中右下角所示的路径执行流程。在模块一中将JCA模型参数孔隙率、流阻率、弯曲度、黏性特征长度和热特征长度，以及物理参数泊松比、阻尼损耗因子、杨氏模量和密度进行编码生成二进制的染色体种群，而后经过解码带入JCA模型中计算吸声系数αS，将该吸声系数与吸声系数实验结果带入目标函数中计算，此时遗传算法会选择出目标函数结果较小的种群个体做遗传下去，接下来经过模块四计算生成新的种群，重复进入模块三中进行筛选，不断地往复循环直到筛选出的种群中个体所求目标函数平均值公差满足收敛标准，即小于等于10-6。通过上述设置的算法迭代终止条件，可以保证每次优化的结果对基本一致。

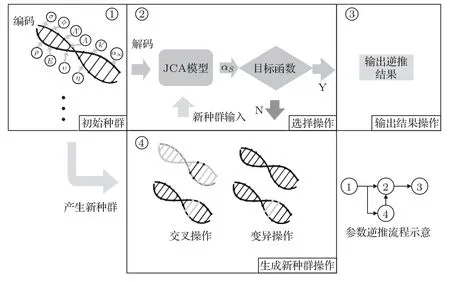
图1 参数逆推原理图Fig.1 Schematic diagram of parameter inversion

关于目标函数，根据现有文献分析文章中多采用最小二乘法作为目标函数逆推模型参数[18]，本文为了提升逆推结果的准确性，提出了如下的目标函数关系式：

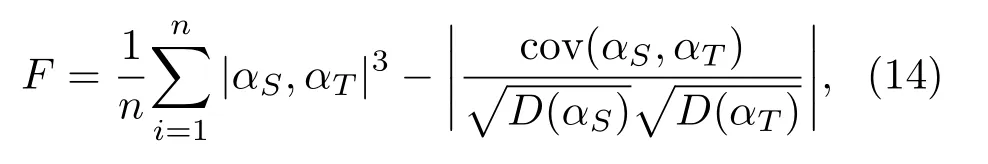
其中，cov(αS，αT)是仿真和实验得到吸声系数的协方差，D(αS)和D(αT)是它们的方差。

2.2 制备测试样品

测试样品为直径44.44 mm 的圆柱体，采用圆形的刀模旋转切割得到，刀模切割后的样品可直接用于Mecanum 公司生产的中号44.45 mm 管径的阻抗管测量吸声系数。同时在优化结果验证部分，采用了管壁内径相同的样品厚度切割设备，保证截面的平整度。

2.3 阻抗管测试

阻抗管测试主要应用于两部分的验证，首先是所建立的多层多孔吸声理论模型的验证，然后是优化之后结构与未优化前结构的性能表现验证。

3 结构参数优化方法

多层多孔材料的结构顺序和各层厚度参数的变化都会对整体结构吸声效果产生影响，本文从两方面考虑优化多层结构的结构参数，分别是材料摆放顺序和厚度参数。如图2所示，A、B、C 三种材料叠加放置，共有6种组合方式。每种结构的总厚度为108 mm，优化目标是寻找每种结构的最优吸声配置，同时将结构总厚度降低至90 mm，因此需要采用最优化方法对结构中各层材料厚度值进行优化，但是考虑到吸声棉厚度无法改变，故本文只针对聚氨酯发泡材料A、B进行厚度值优化。

图2 多层结构顺序示意图Fig.2 Schematic diagram of multilayer structure sequence

本文采用遗传算法进行结构参数优化，优化过程如下：

(1)建立优化模型

为保证厚度减少后结构的吸声能力尽可能高，采用的目标函数为100～4500 Hz 频段下吸声系数的总和，并且优化过程中遵循目标函数在条件范围内取最大原则：

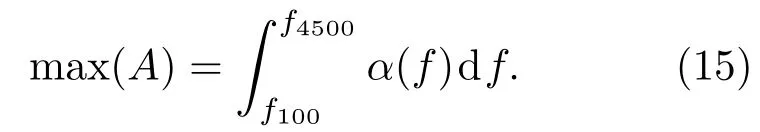
目标函数离散化表示：

其中，αi是对应频率下的吸声系数，Δf是吸声系数求解时频率步长。

(2)约束条件设定

约束条件的设定需要根据结构应用的设计约束，包括总厚度、各个组分的厚度范围。本文假设3 层结构的总厚度为90 mm，各个组分的厚度范围10～90 mm，则约束条件表达式为

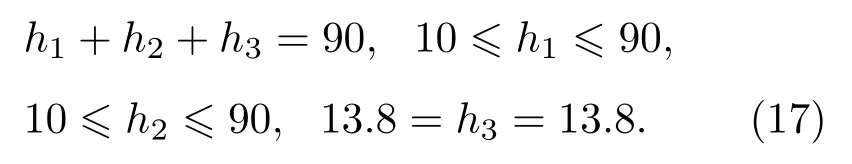
4 结果与讨论

4.1 模型验证与仿真优化结果

为验证理论模型的准确性，利用阻抗管测试了每种结构的吸声系数。同时求解了结构优化前后吸声系数的仿真结果。最后输出结果为每种结构对应的厚度参数、结构总厚度和面密度。其中面密度ρeq表示单位厚度结构的密度值，计算公式如下：

其中，ρA、ρB、ρC为A、B、C 材料的密度，hA、hB和hC为优化后各材料的厚度。

图3绘制了每种结构的优化前(108 mm)吸声系数测试和仿真结果(点画线和虚线)，以及优化后(90 mm)厚度结构的吸声系数仿真结果(实线)。图3主要是为了证明吸声系数测试结果与模型仿真是否一致，以及利用仿真计算初步分析优化前后吸声系数结果的变化。关于模型验证部分根据优化前仿真和测试结果，除ABC 和BCA 结构的模型计算结果与实际测量在2000 Hz 频率下有较大差异，高频部分一致性较好，同时其余结构在研究频率范围内都表现了较好的一致性。表2列出了每种结构优化之后的厚度参数值、结构总厚度和面密度值。

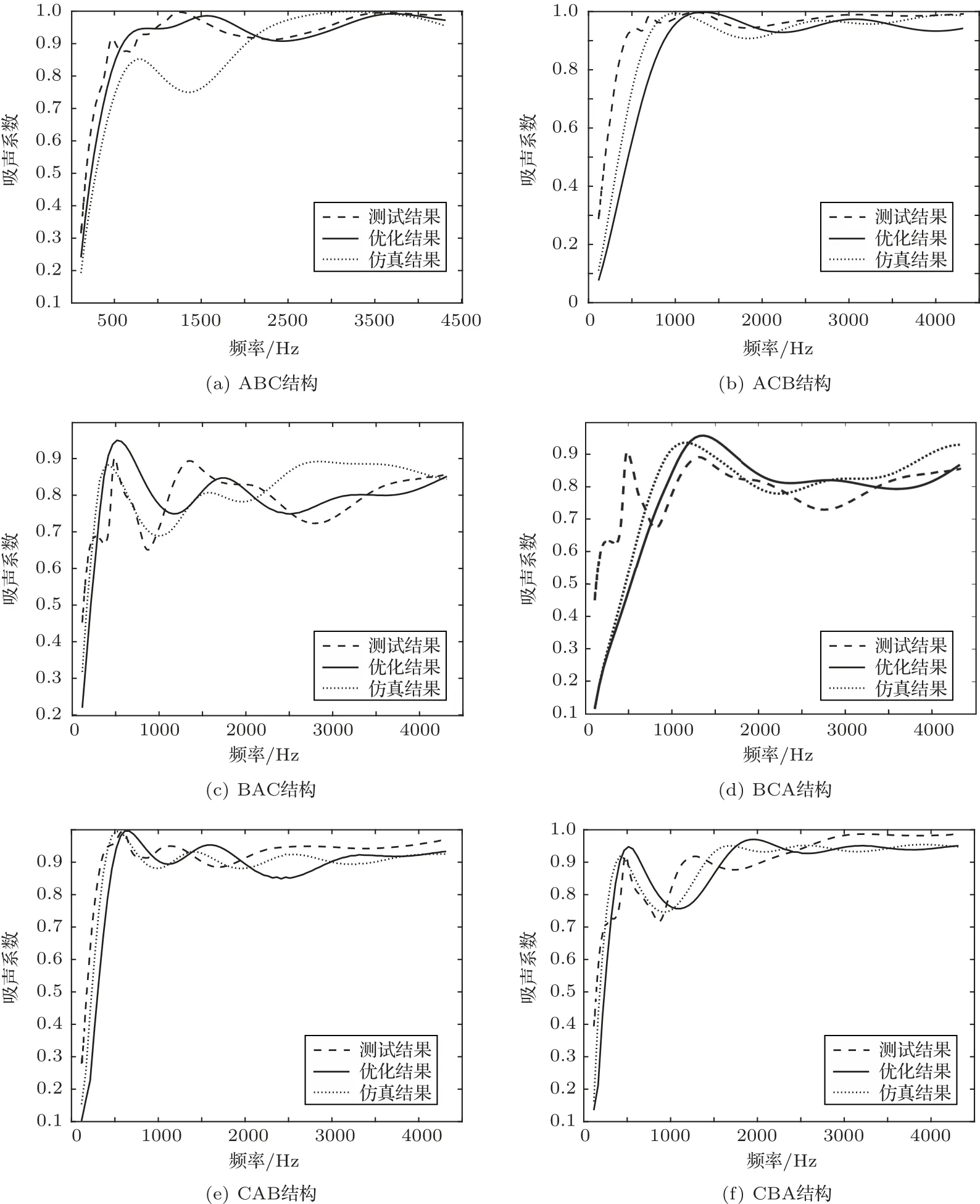
图3 优化前后吸声系数仿真和测试结果Fig.3 Simulation and test results of sound absorption coefficient before and after optimization

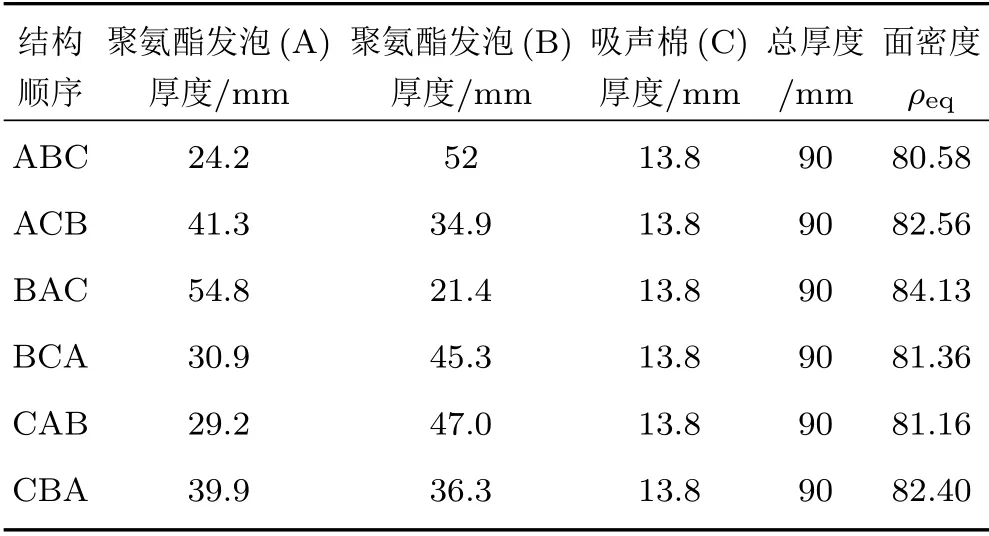
表2 结构参数优化结果Table 2 Optimization results of thickness parameters

4.2 优化结果讨论

本节主要分析优化前后结构总厚度、面密度和吸声性能的变化。表2数据表明，根据优化过程中厚度的约束限制，每种结构的厚度都缩减到了90 mm，比优化之前减少了18 mm。然后根据材料原始厚度值带入公式(18)中计算可知其面密度值为85.01 kg/m3，优化后的结构面密度最大值为84.13 kg/m3，最小值为80.58 kg/m3，都比原始结构小，以上两个指标的提升在结构轻薄程度上都有重大意义。最后根据图3分析优化前后吸声性能仿真结果的变化：结构ABC、BAC、BCA和CBA在低频段的第一峰值吸声系数大小都有明显提升；在高频段(2500 Hz 以上)ABC、BAC、BCA 和CBA 吸声系数优化之后有所降低，剩余结构ACB 和CAB 的厚度优化结果比较符合单层吸声材料厚度减少之后的吸声系数变化规律，吸声系数整体右移。上述前面4种结构低、高频吸声交替变化，后两种结构吸声系数右移的现象，是由于前4 种结构的原始结构对于低频吸声效果较弱，优化之后的结构在中低频段提升明显，因此会产生与ACB 和CAB 截然不同的结果，而ACB 和CAB 的原始结构已经达到了该厚度结构下较好的吸声表现。所以综上所述，本文采用的结合相关理论模型优化结构的方式可以在提升结构轻薄性能的同时，通过厚度参数的优化寻找到该结构顺序下的最佳吸声，而且最佳厚度参数对应的吸声系数往往是可以在一定程度上保证低频的吸声效果的，故具有较大的实际应用价值。

另一方面，上述结论是基于仿真计算得到，接下来采用实验验证的方式判断优化之后的吸声系数是否有所提升，现采用专用的材料厚度切割设备制备了BCA结构的最优结构样品，利用阻抗管测试了其吸声系数，并比较了优化前后样品的吸声系数测试结果，如图4所示。

图4 BCA 结构优化前后测试结果Fig.4 Test results before and after BCA structure optimization

如图4所示，实线表示优化后吸声系数测试结果，实验测试表明优化之后吸声系数在1500～2900 Hz之间的吸声性能提升效果明显，同时在1000～1500 Hz 之间也呈现了较弱的吸声能力提升，对应图3的BCA结构优化前后仿真结果对比发现，其在1000～2900 Hz 之间也有一定的吸声性能的提升，而在1500 Hz 以下和3000 Hz 以上优化前后的吸声实验结果与仿真结果有一定差异，但是并未影响优化之后的吸声系数是该顺序结构的最佳结果，同时也实现了材料的轻薄化和轻量化的目的。

5 结论

本文采用了Biot 模型和等效流体模型JCAL以及TMM 计算了多层多孔吸声材料的吸声系数，并结合遗传算法对3 层梯度多孔材料结构厚度参数优化。最终得出如下结论：

(1)采用JCAL模型、Biot理论结合TMM推导的多层多孔吸声结构的理论模型具有一定可行性，准确度较高，可用于多层结构的仿真研究。

(2)采用遗传算法对多层结构的厚度参数优化研究，可以减少整体结构的厚度、重量，同时结构ABC、BAC 和BCA 在低频段的吸声系数都有明显提升，该方法具有很强的实际应用价值。

(3)本文提出的研究方法所取得的研究成果对于实现结构轻量化，节省安装空间具有重要意义，可应用于高铁、建筑等领域。