散热片对变压器声辐射的影响及优化分析*

胡静竹 王延召 邓银凤 黎 胜 周 兵 张建功

(1 中国电力科学研究院有限公司 电网环境保护国家重点实验室 武汉 430074)

(2 大连理工大学船舶工程学院 大连 116024)

0 引言

随着越来越多的变电站建于居民区和商业区内，变压器噪声问题变得十分突出[1-3]。变压器噪声水平的高低，已经成为了衡量变压器生产厂家设计和制造水平的重要指标。为了保证居民不受噪声干扰，供电部门对变压器的噪声性能提出较高的要求。对居民配电变压器的振动和声辐射问题进行研究十分必要。

变压器振动噪声主要由变压器内部铁芯和绕组电磁力激励产生[2-5]，通过变压器油以及连接夹件传递到油箱表面，进而向外辐射噪声。目前国内外对变压器噪声研究主要集中于铁芯噪声[6-8]，辅助噪声控制技术[9-11]、变压器声源计算模型[12-15]等，对配电变压器油箱及表面散热片辐射噪声进行预估和优化的研究比较少，变压器表面结构的振动噪声问题还有待深入研究。

本文以一台10 kV 油浸式电力变压器(S13-M-200/10)作为研究对象，通过实验测量了变压器油箱和散热片振动加速度分布情况，建立了考虑油箱结构与变压器油流固耦合作用的变压器表面结构振动和声学分析模型，分析散热片振动效应(Vibrating effect)、声源效应(Source effect)和声障效应(Obstacle effect)，结果表明散热片对变压器有不可忽略的声场影响。为了降低变压器的振动噪声，对散热片进行优化，运用遗传算法搜索结构表面振速均方值最小时散热片的尺寸，为变压器声辐射控制提供了参考。

1 散热片的声场效应和评判准则

1.1 散热片的声场效应

变压器散热片结构对于油箱结构的影响相当于肋骨对加肋板的作用，主要体现在3 个方面：振动效应、声源效应和声障效应[16]，这3 种效应可具体解释如下：

(1)振动效应是指加强构件如肋骨等会改变结构的振动固有特性和响应。

(2)声障效应是指肋骨在板的辐射声场中会有障碍物的作用，并因此改变了板的辐射声场。

(3)声源效应是指肋骨表面振动也产生声辐射，也就是肋骨本身也是声源。

在对加强构件改变结构振动声辐射特性的研究中[16-19]，通常会将加肋结构和非加肋结构的声辐射效率进行比较，但声辐射效率并不能很好地表征振动效应、声源效应和声障效应，为此需要更加准确的评判准则来描述散热片对变压器的声辐射影响。

1.2 评判准则

为了评估散热片的影响，本文比较分析了两种变压器构型：油箱包含散热片和不包含散热片，分别为构型1 和构型2。但在探讨散热片的声源效应和声障效应时，油箱包含散热片的构型1 是有区别的，如图1所示，在讨论声源效应时，原始构型1 中的散热片有振动速度；在讨论声障效应时，构型1 中的散热片视为刚体障碍物，即散热片的振动速度为0。图中Vp表示油箱壁的振动速度，Vr表示散热片的振动速度。

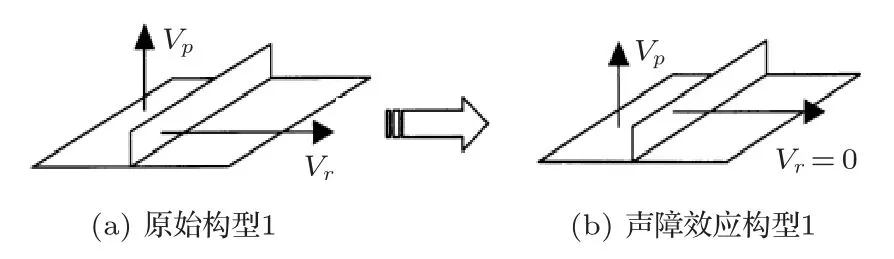
图1 声源效应和声障效应的构型1Fig.1 Configuration 1 for source effect and obstacle effect

Moyne 等[16]指出相关性系数coh 可用来评估声源效应和声障效应。相关性系数coh 比较了两种构型之间声场场点声压的相似性，coh 取值为1 时表示两种构型声场有一致的对应关系，取值为0 时则表示没有一致的对应关系。研究散热片对声场的贡献时，如果某些情况下coh＜0.7，则认为散热片的声学效应(声源和声障)是不可忽视的。相关系数coh 的表达式为

式(1)中：p是声压矢量，p=p-p〉，〈p〉是声压p的平均值。1 和2 表示两种构型，1 对应有散热片的油箱结构，2表示没有散热片的油箱。

通过计算能量E准则[16]研究散热片的声源效应，

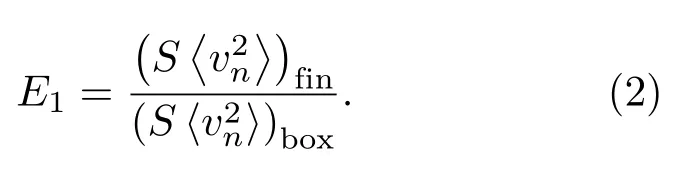
辐射表面声功率与S〈v2n〉成正比，式(2)中(S〈v2n〉)fin是关于散热片的，(S〈v2n〉)box是关于油箱壁的。S是辐射面积，而〈v2n〉是振动表面的法向均方速度，定义为

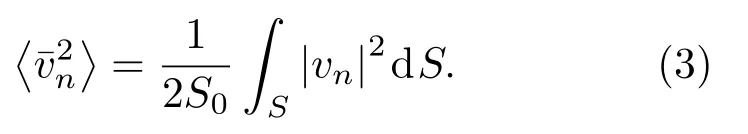
该准则将散热片的振动声功率与油箱壁的进行比较，E1值越高，散热片声源效应越明显。为了更直观地了解散热片声源效应对整个结构的贡献，本文提出一个新的指标：

式(4)中，(S〈v2n〉)s是关于整个变压器结构的，准则将散热片的振动声功率与整个结构进行比较。能量指标E2与E1一样只需知道结构的几何形状和振动特点，不需要关于结构声学特性的任何信息，同时E2的数值范围是0 到1，越接近1 表示散热片声功率对声场的贡献越大，从而不会像E1存在大于1 或是更大的数值，方便直观的比较。

2 散热片对变压器声辐射影响的数值分析

2.1 变压器表面结构

进行有限元建模时，综合考虑计算精度和模型计算，对油箱模型做了简化，忽略油箱上的孔，将油箱视为厚度均匀的封闭箱体[20]。同时去掉油箱上的固定支座，由于实验时油箱通过木板放置在地上，将固定约束直接施加在油箱底部的有限元节点上。简化后的有限元模型如图2所示。

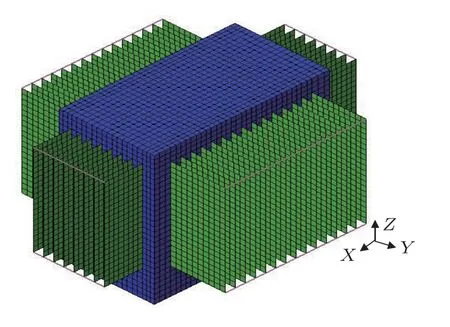
图2 有限元分析模型Fig.2 Finite element analysis model

变压器油箱长740 mm，宽400 mm，高640 mm，厚4 mm，散热片连接柱横截面是1 mm×1 mm 的矩形。表面分布大量垂直于油箱的散热片，其对应参数如表1所示。油箱、散热片及散热片连接柱的材料都为钢材，弹性模量为2.1 GPa，泊松比为0.3，密度为7850 kg/m3。油箱和散热片均采用四边形壳单元shell63 进行模拟，连接柱选用梁单元beam188进行模拟。变压器油箱内部浸满变压器油，需要考虑变压器油流体与油箱结构固体之间的相互耦合作用，选用fluid30 单元模拟变压器油，设定变压器油的密度为895 kg/m3，声速为1390 m/s。

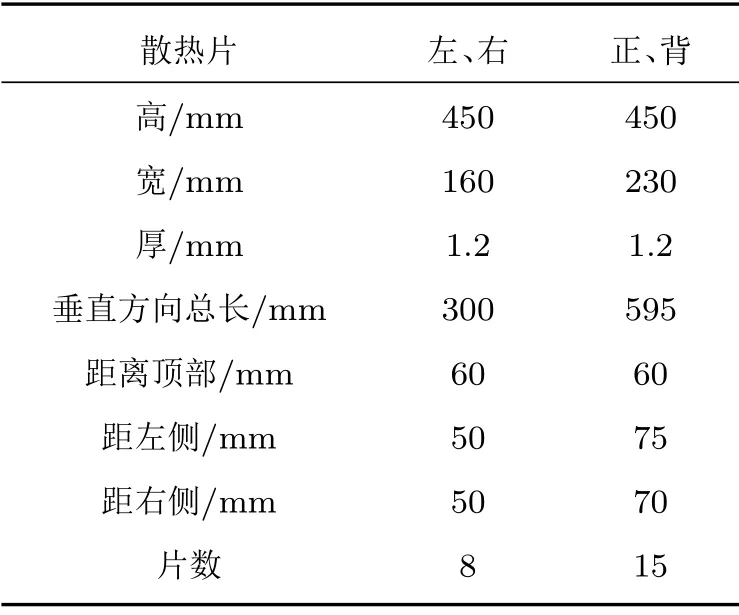
表1 散热片参数Table 1 The parameters of fins

为了得到相关性系数coh，场点声压p的计算共设计了672 个场点，如图3所示，散热片位置处的场点比较密，主要在两个散热片之间，四周场点相对稀疏，场点间距为0.1 m。

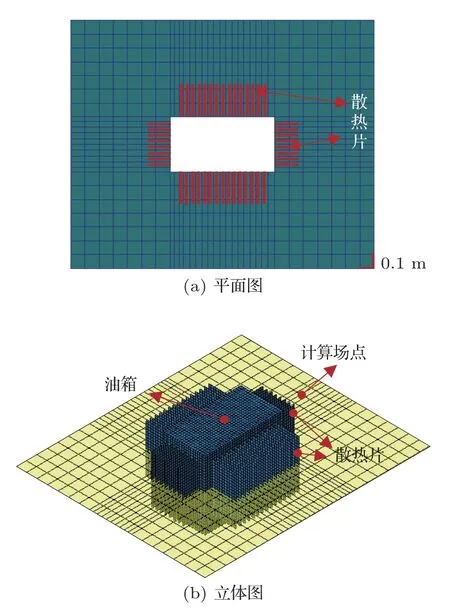
图3 声压计算场点分布图Fig.3 Acoustic pressure field points

2.2 散热片对声场贡献实测分析

以1/3 倍频程形式测量得到油箱和散热片在25～2500 Hz 频带范围内的表面振动加速度数据。油箱正面与散热片振动加速度测点位置如图4所示，油箱正面中间测点与正面最右侧散热片中间测点的振动加速度随频率的变化如图5所示。

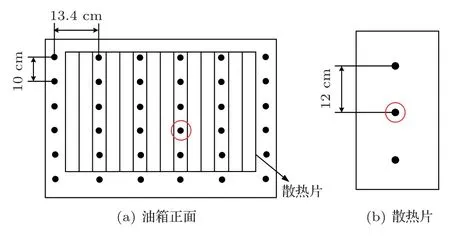
图4 油箱正面和散热片测点布置示意图Fig.4 The arrangement of the measuring points on the front of box and the fin

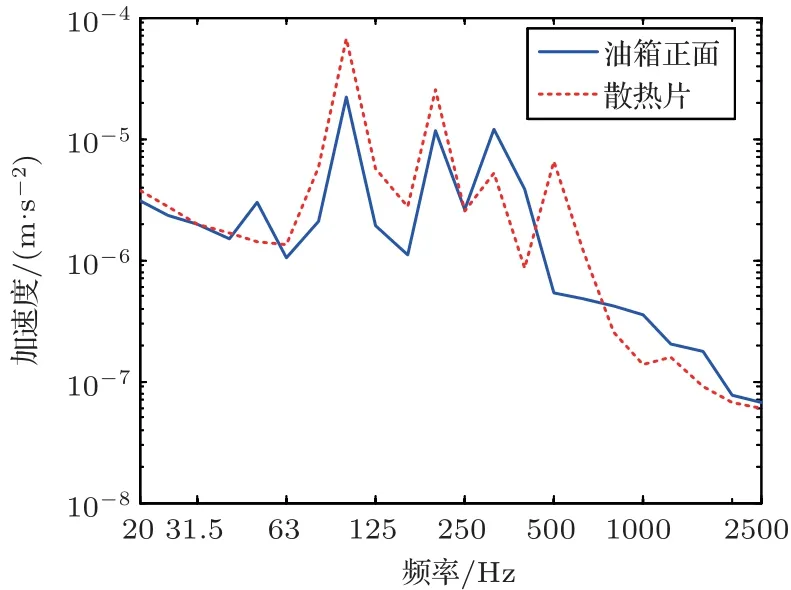
图5 油箱正面和散热片测点振动加速度Fig.5 The vibration acceleration of the measuring points on the front of box and the fin

由图5可观察到，加速度的峰值主要集中在100 Hz、200 Hz 和300 Hz，散热片振动加速度比油箱本体正面加速度还要大，可知散热片对声辐射的贡献有不可忽略的影响。

图6给出加速度值较大的100 Hz 和200 Hz 频率下的油箱表面加速度云图，从图6中观察到，油箱加速度幅值最大的位置一般在油箱的中下方或者两侧，对照图2的结构有限元模型，这两个位置对应散热片与油箱连接处的末端和没有散热片连接的油箱两侧，表明散热片会对油箱的振动方式产生影响。为探讨散热片对声场影响的振动效应、声源效应和声障效应，下面将通过模态分析和施加单位力进行频率响应分析来分析散热片对变压器声场的影响。

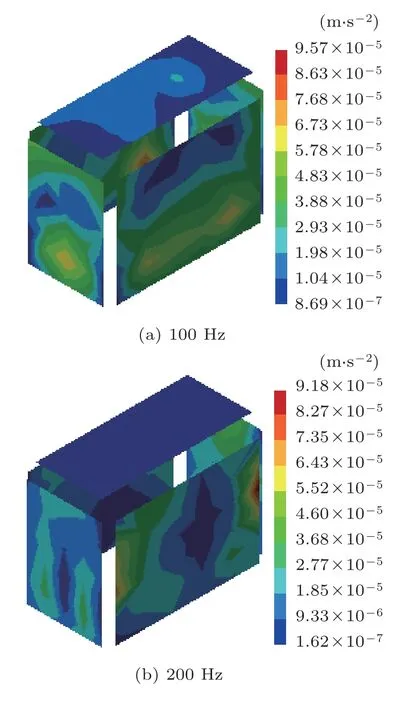
图6 油箱表面加速度云图Fig.6 Acceleration contour of the box

2.3 模态分析中散热片对声场的贡献

本文利用有限元对箱体填充了流体单元，对箱体在流固耦合下进行了模态分析。流固耦合系统的有限元方程为

其中，M、K分别为固体质量矩阵和固体刚度矩阵，Mf、Kf分别为流体质量矩阵和流体刚度矩阵，R为流固面上的耦合矩阵，p为流体压强，x为位移向量，ρ为流体介质密度。模态分析可以求出考虑变压器油耦合作用的变压器表面结构固有频率和振型。

表2是油箱有无散热片两种构型在有无填充变压器油模态分析得到的前10阶固有频率，由计算结果可以看到考虑变压器油时结构固有频率会更低一点，油箱有无散热片两种构型的固有频率完全不同，有散热片油箱的固有频率远大于没有散热片的。

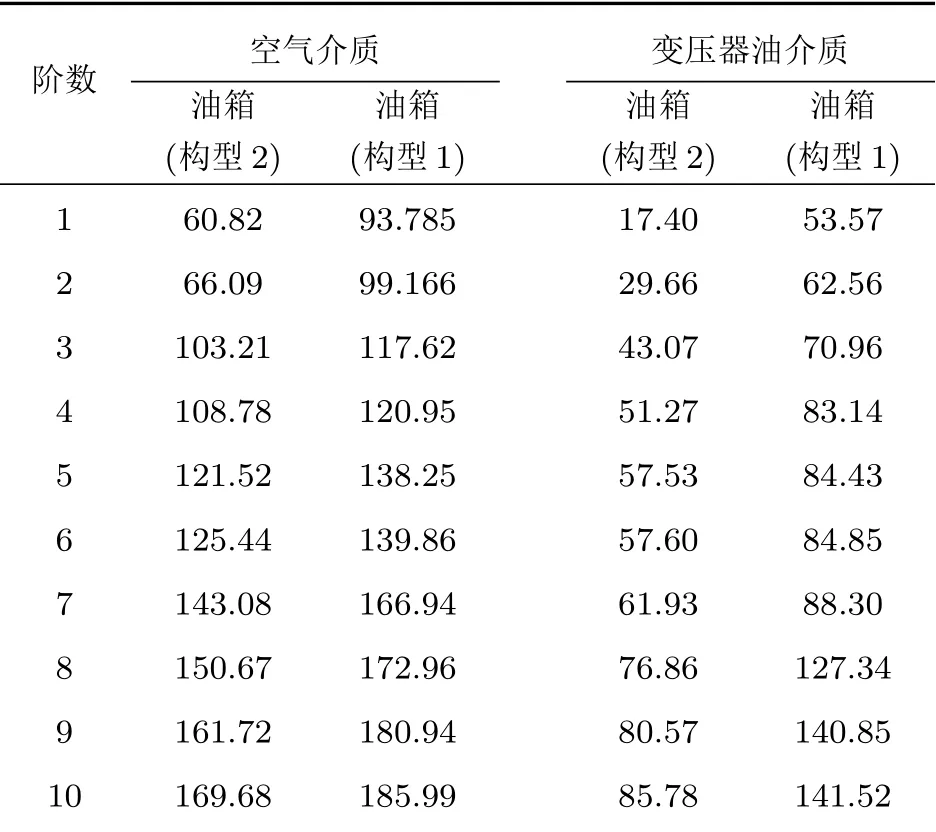
表2 模态分析的固有频率Table 2 Nature frequencies of normal mode(单位: Hz)

图7是两种构型含变压器油模态分析得到的第三阶振型，从图7可以看到，两种构型的振型也是不同的，散热片连接的油箱板块(前、后、左、右侧板块)的振型峰值主要在油箱板块的中下方，即散热片与油箱连接的末端处。这也表明散热片作为结构构件的振动效应是必须要考虑的。

图7 模态分析的振型Fig.7 Mode shape of normal mode

以模态分析的振型结果作为声学边界条件进行声学仿真，得到如表3所示的散热片声源和声障效应指标的计算结果。

相关系数coh表征两个构型场点声压形状的相关性。表3中油箱有无考虑变压器油的coh 均小于0.7(除第二阶)，说明散热片对声场分布影响很大，散热片的声学效应(声源和声障)在声辐射是不可忽视的。能量指标E2表征散热片的声源效应，表3中E2的数值有很大部分接近1，尤其在高阶模态上，说明散热片在变压器表面结构中所占的声功率比值非常大，散热片声源效应明显。

表3 声源和声障效应指标的计算结果Table 3 Criterion results of source effect and obstacle effect

2.4 频率响应分析中散热片对声场的贡献

油箱有无散热片两种构型在有无填充变压器油两种情况进行频响分析。在节点1051(变压器前侧中间散热片与油箱连接的末端处)作用单位力1 N，方向沿结构表面法向远离油箱，频率范围是25～300 Hz。图8是在200 Hz频率下两种构型考虑变压器油的位移响应云图。

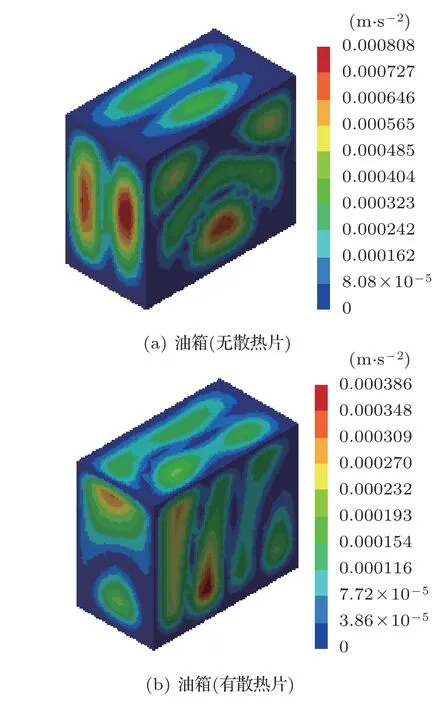
图8 频响位移云图Fig.8 Displacement contour of frequency response

从响应变形云图可以观察到，两种构型的变形方式会有所差异，有散热片油箱的相应峰值主要在油箱板块的中下方或上方，即散热片与油箱连接的末端处或没有散热片的位置，而且有散热片油箱的响应峰值小于无散热片的油箱。散热片不但改变油箱的振动方式，还能降低箱体的响应幅值。

以频响数据作为声学边界条件进行声学仿真，得到如表4所示的声源效应和声障效应的计算结果，表4中油箱有无考虑变压器油的相关系数coh均小于0.7 (除不含变压器油的50 Hz)，说明散热片的声学效应(声源和声障)在声辐射是不可忽视的。声源效应的能量指标E2的数值大部分大于0.5 (除50 Hz)，说明散热片的声功率所占比例大，其声源效应明显。

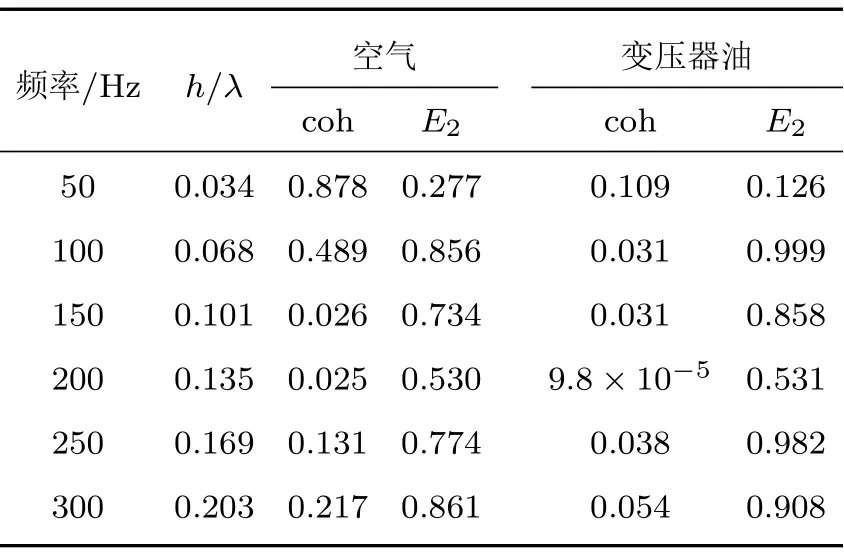
表4 声源和声障效应的计算结果Table 4 Criterion results of source effect and obstacle effect

3 散热片位置和尺寸的优化

3.1 基于遗传算法的均方速度最小化

本文研究的散热片对变压器有不可忽略的声场效应，为此可通过对散热片优化来降低变压器的振动噪声。实验测量得到变压器表面结构的加速度值在100 Hz、200 Hz 和315 Hz 的幅值最大，为此将在100～300 Hz 频段内对散热片进行优化。油箱下表面处理成固支边界条件，变压器油箱内部浸满变压器油，考虑变压器油流体与油箱结构的流固耦合作用。由于变压器内部结构振动机理复杂，从绝缘油与连接件传递的振动能量暂时无法考虑，为了更接近实际情况，本文将激励设在变压器油箱测试实验中振动最大点处，即油箱正面散热片下部连接处，也是绕组中心位置对应处，激励大小为1 N，计算频率范围为5～300 Hz。

散热片优化通过集成ANSYS 与MATLAB，应用遗传算法进行优化设计。由于ANSYS 自带的参数化设计编程语言很难将优化算法直接写入ANSYS[21]，因此可以利用ANSYS的二次开发接口，通过中间平台Matlab 调用ANSYS，使其读取Matlab产生的种群数据进行有限元分析，再由Matlab读取ANSYS 有限元分析后输出的表面法向振动速度值，并采用法向振速均方值在一定频率段下的平均值来进行个体筛选，形成新的种群，最后在Matlab 中进行算法优化，以此获得最优解。

在优化中将变压器散热片的宽度、高度和厚度作为设计变量，并设散热片不会超出油箱壁，将变压器表面结构法向振速均方值在一定频段下的平均值为目标函数，优化方程可写成：

式(6)中：xli和xui为所定义的设计变量的上下限，ω2和ω1为所分析频率的上下限；约束条件h(x)还包括变压器的散热量和结构重量等。

3.2 散热片宽度的优化分析

在散热片宽度优化分析中，散热片的高度H不变，为保持散热片结构的总面积不变(散热片的散热值保持不变)，正背面与左右侧面散热片的总宽度需保持不变，即FF+FL = 0.39 m，其中FF 表示正背面散热片的宽度，FL 表示左右侧面的高度。将正背面散热片宽度FF 参数定义为设计变量，在这种优化模式中满足0.1 m ≤FF＜0.39 m。为保证散热片总面积不变，则左右侧面散热片宽度为FL=0.39 m-FF。

优化后，正背面散热片宽度为FF = 0.2494 m，左右侧面散热片宽度为FL = 0.1406 m，min〈〉e为54.74 dB，这里振速均方值用公式(7)dB 单位表示：

其中，a为振速均方值的幅值，参考值a0为10-12m2/s2。

图9为结构在优化前后的表面结构振速均方值，很明显地抑制了响应的峰值，而且还降低了100 Hz、200 Hz和300 Hz附近的振速均方值。图10是优化散热片宽度的解和种群平均值的变化。

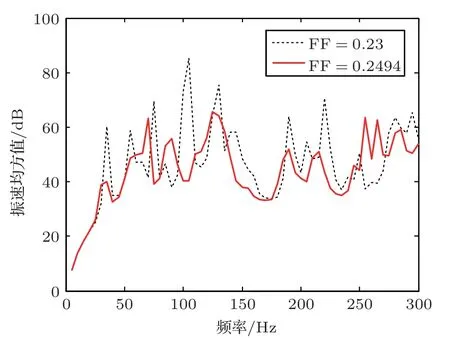
图9 优化散热片宽度的振速均方值Fig.9 Mean square velocity of the optimized fin width

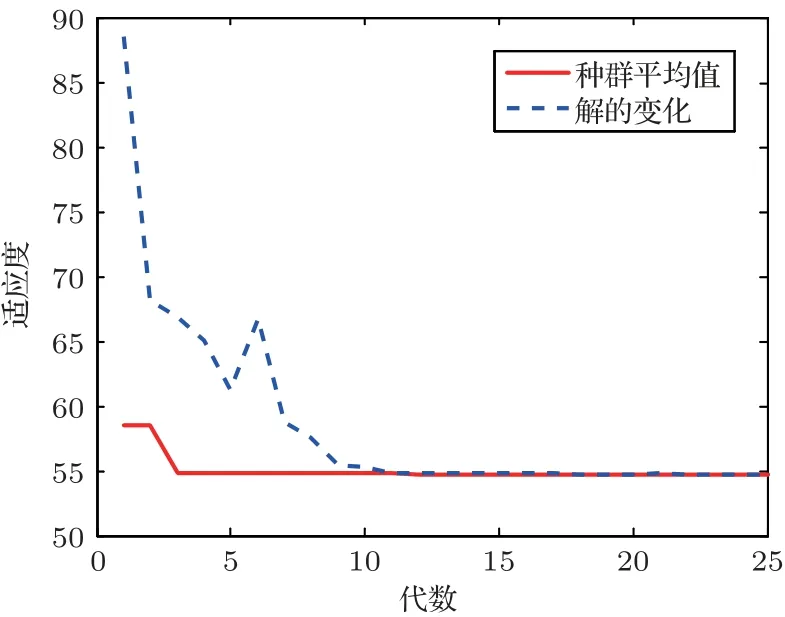
图10 优化正背面散热片宽度的解和种群平均值的变化Fig.10 Best fitness and mean fitness of the optimized fin width

为验证优化方法对于降低辐射声功率的可行性，将优化散热片后的表面振动响应作为声学边界条件进行声学仿真，计算得到优化后的辐射声功率如图11所示，优化后的散热片明显降低声功率的峰值，达到降低声辐射的效果。表明结构表面法向均方速度最小为目标函数是可行的，优化后的散热片可以降低一定频率范围内的辐射声功率。

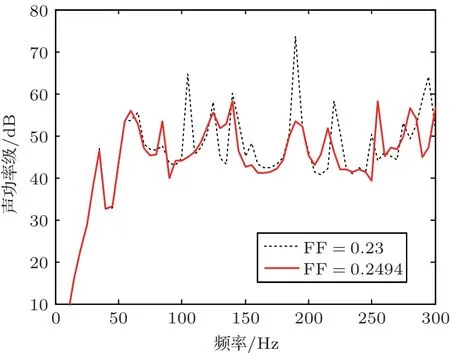
图11 优化散热片宽度的声功率Fig.11 Sound power of the optimized fin width

3.3 散热片高度对声辐射的影响

在散热片高度优化分析中，为保持散热片结构的总面积不变，改变高度，散热片的宽度也随之改变。将散热片高度H参数定义为设计变量，在这种优化模式中满足正背面和左右侧面散热片的高度相同，H不会超出油箱并满足0.35 m ≤H≤0.5 m。

优化后，散热片高度为H= 0.4979 m，为保持总面积不变，正背面和左右侧面散热片宽度优化后分别对应为FF = 0.23×0.45/H= 0.2079 m，FL = 0.16×0.45/H= 0.1446 m，min〈〉e为52.87 dB。图12为结构在优化前后的表面结构振速均方值，很明显地抑制了低频的前几个表面结构振速均方值的峰值，而且还降低了100 Hz、200 Hz 和300 Hz 频率附近的振速均方值。表明通过优化散热片的高度，能有效地降低变压器表面结构的均方速度。

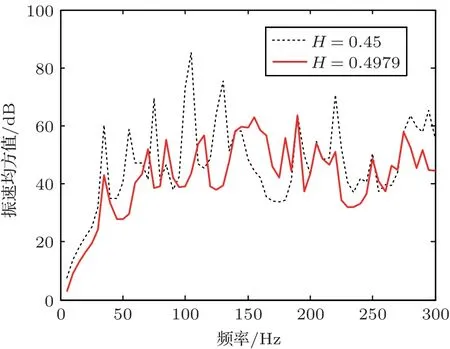
图12 优化散热片高度的振速均方值Fig.12 Mean square velocity of the optimized fin height

3.4 散热片厚度对声辐射的影响

在声辐射优化分析中，假定散热片结构的总面积保持不变，将散热片厚度参数定义优化后，在这种优化模式中，只改变散热片的厚度T，并满足0.0009 m ≤T≤0.0025 m，在采用ANSYS 进行结构优化分析时，通过设置实常数改变散热片厚度。优化后，散热片厚度为T= 0.0023 m，min〈〉e为56.88 dB。图13为结构在优化前后的表面结构振速均方值，图中表明通过优化散热片的厚度，也能有效地降低变压器表面结构的均方速度。

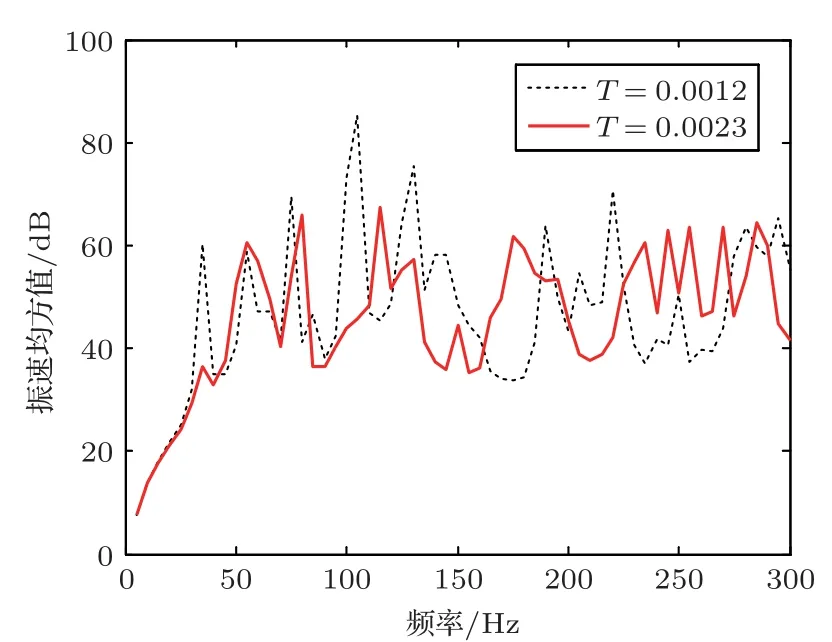
图13 优化散热片厚度的振速均方值Fig.13 Mean square velocity of the optimized fin thickness

4 结论

通过仿真分析了散热片的振动效应、声源效应和声障效应，并计算相关系数coh 和能量E准则定量描述散热片的声障效应和声源效应，在此基础上应用遗传算法通过优化散热片分布位置和尺寸来实现改变结构的表面振动并减少声辐射，得到如下结论：

(1)散热片作为结构构件的振动效应是必须要考虑的。散热片会增大结构固有频率和改变振型，实验测量得到的加速度云图和频响分析的响应云图相似，主要是连接散热片的板块发生了改变，变形的峰值集中在油箱的中下方，油箱中下方位置对应散热片与油箱连接的末端处。

(2)相关系数coh 基本小于0.7，表明散热片的声源声障效应在声辐射中是不可忽视的。表征声源效应的能量指标E2在模态分析和频响分析中大于0.5，在模态分析中甚至接近于1，表明散热片的声源效应非常明显。

(3)通过优化散热片的高度、宽度和厚度均可在一定程度上减小变压器油箱结构的均方振动加速度，同时也达到了降低辐射声功率的作用，优化散热片结构分析方法可为变压器降噪提供依据。