基于钻孔灌注嵌岩桩容许承载能力的研究

王 猛

(广东交科检测有限公司，广东广州 510426)

0 引 言

因具有较高承载力,嵌岩桩被广泛应用于桥梁桩基中[1]。但在实际项目中,嵌岩桩试验较为困难,持力层与桩岩间的相互作用规律还有待进一步研究[2,3]。当前,多以半理论半经验的方法计算桩基竖向承载力,但因各地区所处环境不同,计算结果存在较大的偏差[4-6]。其中,最直接有效确定嵌岩桩承载力的方式是基桩的原位测试,故本文将据此对桩基竖向承载力进行研究。

1 工程概况

牛田洋特大桥共分北岸公轨共建段、牛田洋大桥北引桥、牛田洋大桥主桥及牛田洋大桥南引桥26#～44#墩四部分,牛田洋特大桥0#～30#墩直线距离3 908.2 m,其中主桥为公轨两用钢桁梁斜拉桥,跨径布置为(77.5+166.1+468+166.1+77.5) m,设计时速为100 km/h。主塔基础为钻孔灌注桩,桩尖进入中风化花岗岩。

2 有限元模型分析

2.1 有限元模型

为提高模型模拟现场的准确性,本文从考虑单桩承载力与边界约束条件关系的角度出发,将模型长度和宽度限制在15D内。桩长以现场试桩长度为准,以现场地质条件设置模型岩土层,经分析,对于单桩承载力而言该种取法对其影响较小,符合设计要求。以线弹性模型模拟桩身混凝土;按照X、Y方向对模型岩土层侧面进行约束,以固定约束的方式模拟模型底部;单元按照整体形式进行划分,拟定0.2 m作为桩身单元的尺寸,拟定0.7 m作为岩土体单元尺寸,拟定1 m作为桩端底部单元。模型单元以六面体为主。有限元模拟参数详见表1和表2。

表1 有限元模拟土层参数

表2 桩单元和桩端单元模拟参数

为分析不同因素影响下,嵌岩桩的荷载传递情况,本文通过能够有效模拟岩土和混凝土材料的MIDAS/GTS对其进行建模处理,以取得各级荷载下桩基位移及应力变化情况。因岩土情况较为复杂,本文在对试桩进行模拟时做出了以下假定:

(1)单桩在作用竖向荷载时主要处于空间轴对称状态,以平面轴对称的方式进行分析模拟。

(2)基于工程实际,各个土层的模型在建立时均采用同种计算参数。

(3)以线弹性模型进行桩身混凝土的模拟,以Drucker-Prager模型进行基岩和土层的模拟。

2.2 自平衡试桩结果与有限元分析结果对比

为确定单桩容许承载力,本文在确定其单桩竖向承载力时主要考虑了桩身材料强度和桩周土的影响。本文随机选取了现场2根试桩进行建模分析,以通过对比试验结果和计算结果的方式来确定各试桩的容许承载力。桩身竖向容许承载力在基于桩身材料的基础上进行计算时为:

[P]=φ[σc](Ac+mAs)

(1)

式中:As为受力筋截面面积;m为混凝土与钢筋的强度之比;Ac的为桩身截面混凝土面积;φ为纵向弯曲系数。

基于桩身HRB500钢筋及混凝土材料进行计算可得,该试桩具有10 000 kN的容许承载力,并须确保其桩顶位移小于40 mm。

(1)自平衡数值模拟。试验以1级1 000 kN,共10级的方式进行加载,所得各个加载情况下桩基极限承载力如图1所示。

图1 自平衡数值模拟加载分级及位移量图

在8 000 kN的荷载作用下,荷载箱的数值模拟结果为4.3 mm的向上位移以及-9.1 mm的向下位移;实测数据表明,现场加载时荷载箱有着4.87 mm的向上位移以及-6.03 mm的向下位移;对比发现,两种数据较为接近。

荷载箱底的位移因自平衡上下桩之间的作用力与反作用力效果,使得桩身在荷载相同时的桩端位移在因桩身压缩的情况下较小。此外,对比箱底位移和桩顶位移发现,荷载箱顶具有更大的位移。

自平衡数值模拟等效荷载下试桩桩基位移见表3。

表3 试桩自平衡数值模拟等效荷载位移表

由表3可知,桩基位移在等效竖向荷载13 115 kN之前表现为线性变化规律;但当荷载大于该值时,其位移的变化则表现出非线性规律。表明单桩的容许承载力为13 115 kN。

(2) 传统静载试验数值模拟。模拟结果如图2所示。

图2 试桩荷载位移关系对比图

由图2可知,当荷载为8 000 kN时,试桩桩顶有-10.2 mm的位移产生；当荷载增加到16 000 kN时其位移增加到-24.7 mm,表明桩顶位移与竖向荷载呈正比例关系。分析桩身轴力控制,当荷载为8 000 kN时,其桩底轴力为491 kN,桩端荷载比为6.0%;桩底轴力在荷载上升到12 000 kN时变化到1 045 kN,有着8.4%的桩端荷载比。结果表明设计荷载作用下,桩端仅有较小荷载,即无法充分发挥桩端承载力。

桩周土层的位移在同一水平面上随着桩身间距的不断上升呈现出不断下降的规律;桩周岩土层在竖直方向上的位移整体上表现出递减的规律,特别是对于中风化岩周围的桩基而言,其桩侧岩层仅具有少量位移值。当设计荷载为8 000 kN时,桩端岩层的位移值为0.66 mm,当荷载上升到16 000 kN时,桩端岩层位移仍小于1.55 mm。

在12 000 kN的竖向荷载之前,桩顶有着-15.66 mm的竖向位移值,并且在此前其位移均呈现线性变化,当荷载超过12 000 kN之后,其位移曲线布载表现出非线性规律。取12 000 kN作为单桩的容许承载力。

(3)容许承载力的确定。试桩的容许承载力在基于桩身材料和位移、桩周土的前提下,以数值模拟和现场试验的方式进行确定。桩基容许承载力可通过计算岩土阻力来确定,本文依据各项规范对其进行了计算,所得结果为:按照英国规范计算得到的岩土阻力为12 266 kN;按照美国规范所得到的为11 812 kN;法国则为15 141 kN;欧洲则为12 111 kN;依据我国铁路规范计算所得结果为10 501 kN,公路规范计算结果为9 080 kN,建筑规范计算结果为12 336 kN。综上分析确定10 010 kN为其容许承载力。因桩端岩石抗压强度较高,故将其容许承载力的控制因素确定为桩身材料强度。

从上述计算结果可看出,相比之下,依据我国铁路和公路规范所得的计算结果较国外规范小,两者有着20%以上的差距,而按照建筑规范进行计算所得到的结果与国外规范计算结果相近,表明建筑规范与实际较为相符。此外,相比于传统静载模拟所得的12 000 kN容许承载力结果,以MIDAS/GTS有限元分析所得的13 115 kN容许承载力与其仅有9.1%的差距,表明相比之下,按照MIDAS/GTS有限元模型进行分析的方法所得到的嵌岩桩承载力较为准确。

3 嵌岩桩竖向承载理论工程应用

嵌岩桩应结合桩身材料强度和位移,以及桩侧岩土阻力等来确定其单桩承载力。将上述试桩所得到的基本规律应用于牛田洋特大桥的嵌岩桩中,桩基岩土参数见表4。

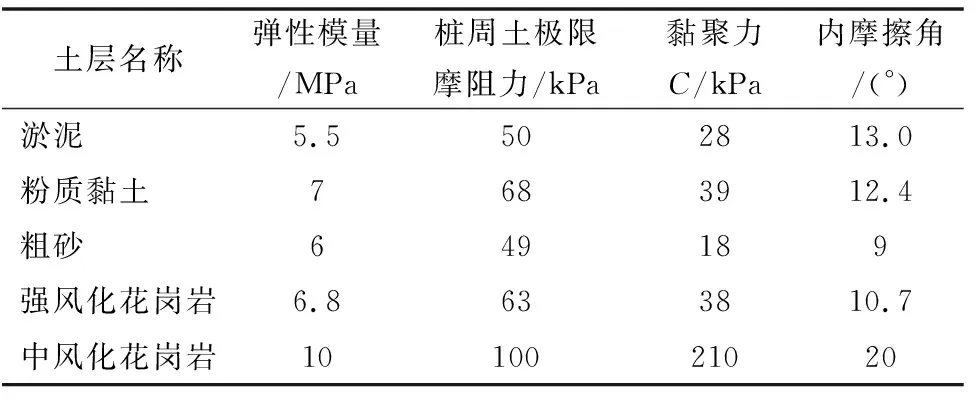
表4 桩基岩土参数

桥梁墩基础均为2.5～3.0 m桩径的钻孔灌注桩基础。基于地质调查报告,采用MIDAS/GTS有限元软件进行建模分析。模拟结果如图3所示。

图3 模拟荷载位移关系曲线图

由图3可知,桩顶在7 000 kN的荷载作用下有着-14.25 mm的竖向位移；在7 000 kN的荷载之前,位移呈现线性变化,当荷载超出7 000 kN后,位移曲线呈现非线性变化,故将比例界限确定为该点，即桩基的容许承载力通过MIDAS/GTS模拟桩侧岩土阻力所得到的结果值为7 000 kN。桥梁桩基所采用混凝土等级为C35,箍筋采用HRB 500级,其余钢筋均采用HRB 400级。基于桩身材料计算所得容许承载力为13 810 kN。

因桩端所处中风化花岗岩层的弹性模拟值较高,故以4 000 kN和8 000 kN计算所得的桩身位移较小。

依据国外规范和中国规范对其承载力进行计算,结果表明依据法国规范计算得到的承载力最大,其值为7 800 kN。依据传统静载进行的MIDAS/GTS有限元模拟分析结果显示桩基有着7 000 kN的容许承载力，对比可知依据经验公式和外国规范进行计算所得到的容许承载力相差较小。为使桥梁具备足够的安全性以及经济性,最终将桩基的容许承载力确定为7 000 kN。桩顶在主要荷载组合下有2 290 kN的荷载值,故该桩基设计满足要求,并且有着较富余的承载力,在该区段进行桩基设计时可适当降低其嵌入深度,以满足经济性要求。

4 结束语

基于嵌岩桩竖向承载机制下,本文以桩身材料强度和位移,以及桩侧岩土阻力三种影响因素,对单桩的设计容许值进行分析研究。根据自平衡模型及试验结果的对比可知,在中国的规范中,地基基础规范计算结果更符合实际受力;采用GST有限元分析模型与传统静载模拟所得结果相近,特别是荷载较小的情况下两种方法所得到的位移试验结果基本重合,表明以MIDAS/GTS有限元模型进行嵌岩桩容许承载力计算时能够取得较准确的结果,但为使模拟结果更具准确度,需有较为全面的现场岩土参数;当桩端所处持力层有较高强度时,应以桩身材料强度作为其容许承载力的强度控制值。