基于差商的插值法拓展思路与教学方法研究

邹 乐，吴志泽，谢 进，檀 明，王晓峰

(合肥学院 人工智能与大数据学院，安徽 合肥 230601)

计算方法又称数值分析、数值计算方法，是一门科学有效计算各种数学问题的数值近似解的课程，具有工程应用的严密科学性和高度广泛性的特点[1-2]。函数插值与逼近论历史悠久，而插值问题是计算数学中的一个最基础的问题。插值问题是指根据给定的离散数据构造一个连续定义的简单函数，使得它与被逼近的函数在给定点的值完全一致。在已知数据点较少时，插值技术在工程实践和科学实验中有着广泛而又重要的应用，如建筑工程的外观设计、图像恢复图像重建、根据离散数据绘制光滑曲线、物理实验中的数据分析与处理、地理信息数据的处理、数值逼近、构造圆弧、图像缩放、图像变形、图像配准等[3]。在数字图像处理的问题中，使用插值方法处理图像重建等，能有效培养学生的科学探究能力、创新思维和计算思维能力[4]。

插值问题在教科书中一般的提法是[2]：若通过某种方法己知函数y=f(x)在区间[a,b]上的一组对应关系{(x0,y0),(x1,y1),…,(xn,yn)}，插值的目的是根据给定数据，寻找一个解析函数P(x)近似地代替f(x)。鉴于多项式具有良好的性质，研究较多的是多项式函数。计算方法课程中主要介绍的是Lagrange多项式，Newton多项式和Hermite多项式三种常见的插值方法[1-2]。本文以Newton插值多项式为基础，结合计算方法课程教学实践和最新的插值研究科研成果，拓展计算方法课程中传统的插值教学方法。首先，基于构造法引导学生探索基于反差商的连分式插值方法，然后，探讨构造基于含参数差商的Newton型插值多项式，最后，研究基于含参数反差商的Thiele型连分式有理插值的构造过程，并给出插值法的多元推广等进一步拓展思路。本文以全新的视角探索计算方法课程中插值与逼近的教学方法，致力于培养学生的计算思维、创新思维与科研探索精神。

1 基于差商的插值法拓展思路分析

1.1 Newton插值多项式

Lagrange插值公式是一种常用的插值公式，构造简单，但在增加插值结点时插值基函数li(x)(i=0,1,…,n)全部要重新构造，不便于实际应用。为了克服上述缺点，在一般的教材中给出了Newton插值多项式如式(1)所示。[2]

Pn(x)=f(x0)+f[x0,x1](x-x0)+…+f[x0,x1,…,xn](x-x0)(x-x1)…(x-xn-1)

(1)

其中系数f(x0),f[x0,x1],…,f[x0,x1,…,xn]是f(x)的各阶差商。

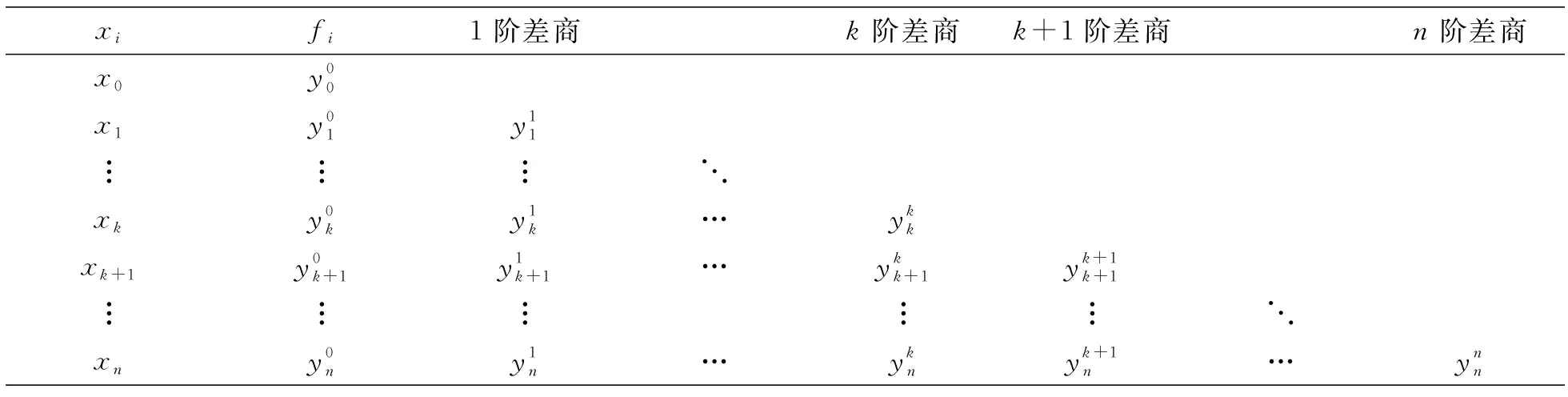
表1 差商表

由多项式的唯一性定理[1]，在n+1个点x0,x1,…xn上构造给定插值数据的次数不超过n的多项式是唯一的。但对于Newton插值公式来说，当增加一个插值节点时，只需在Newton插值多项式的后面添加一项即可，但当节点较多时，高次插值多项式具有不稳定性[2]。

1.2 Thiele插值连分式

为了解决高次插值多项式不稳定性问题，在计算方法课程教学过程中，在基于差商的Newton插值多项式基础上，启发学生思考，将差商倒过来引入反差商，探索有理插值问题，将科学探究精神有机地融入教学过程中，达到润物无声的育人效果。

由上述公式确定的φ[x0,x1,…,xk]为函数f(x)在点x0,x1,x2,…,xk处的k阶反差商。可得反差商表如表2所示。

表2 反差商表

基于表2反差商，可以构造Thiele连分式有理插值[2-3]如式(2)所示。

令

φ[xi]=f(xi),i=0,1,2,…,n

(2)

(3)

…

(4)

(5)

其中φ[x0,x1,…,xk]≠0，∞；k=0,1,…,n。为f(x)在x0,x1,…,xk处的k阶反差商，易证Rn(xi)=f(xi),i=0,1,…,n。

由Thiele连分式插值理论，由(5)式得到的有理插值可以解决了插值多项式的高次不稳定问题，但由(4)式知，k阶反差商φ[x0,x1,…,xk]在构造过程中可能会出现不存在问题，且构造的有理插值可能会存在不可达点[5]。

1.3 含参数Thiele连分式插值

为了解决反差商不存在或者有理插值的不可达点这类特殊插值问题，引导学生发现此类问题的关键所在，培养学生的创新意识和严谨细致的工作作风，锻炼学生的理性思维能力。结合教学实践和最新的插值研究科研成果，给出几种常见的解决方法：①调整插值节点[6]，②用差商代替反差商[7]，③用块反差商代替反差商[3,8]。这几种方法虽然避免了反差商不存在的问题，但是存在不能事先确定调整哪个节点，在何时利用差商代替反差商等问题。近年来，李和Zou等[5,9]提出了含参数的Thiele连分式有理插值，与上述方法相比，含参数的Thiele连分式插值的计算方法更简便实用，便于学生理解和计算机编程实现。

含参数Thiele连分式插值可以分为单个参数和多个参数的情形。含多个参数的情形中一般仅研究双参数情形，而含双参数的一元Thiele型插值多项式的构造又分为含单个三重节点参数化Thiele型连分式插值和含双二重节点参数化Thiele型连分式插值。本节以含单个参数的Thiele连分式插值为例展示含参数差商的构造过程，培养学生的科研创新意识。

考虑将原插值数据点中的任意一点(xk,yk),(k=0,1,…,n)看作一个二重结点，其它插值节点的重数保持不变。

令

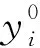
(6)

当j=1,…,k+1，对于i=j,j+1,…,n，如式(7)所示。

(7)

对于i=k+1,k+2,…,n，如式(8)所示。

(8)

当j=k+2,k+3,…,n，对于i=j,j+1,…,n，如式(9)所示。

(9)

可以构造如下形式的含参数λ的Thiele型连分式有理插值，如式(10)所示。

(10)

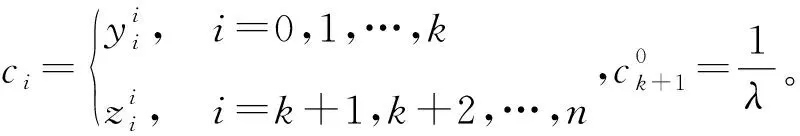
相应于式(6)-(10)的反差商表如表3所示。

表3 含单参数反差商表

下面定理1说明了构造的插值公式(9)是满足插值条件的。

定理1 对于给定的离散各节点互不相同的插值数据{(x0,y0),(x1,y1),L,(xn,yn)}，由式(10)所确定的Thiele型连分式有理插值函数满足插值条件，如式(11)所示。

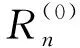
(11)

当i=k+1时，

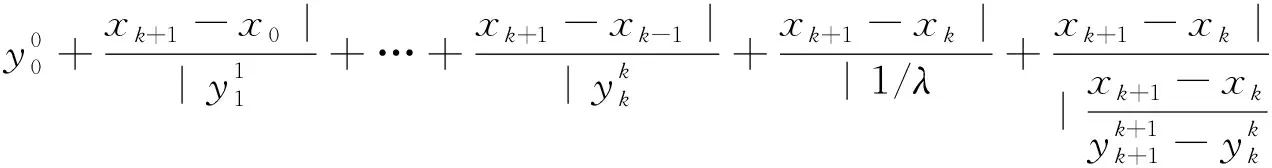
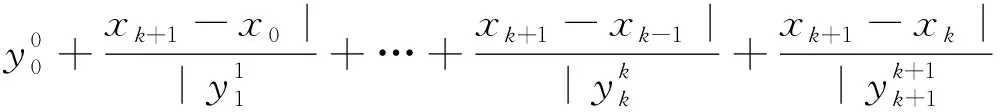
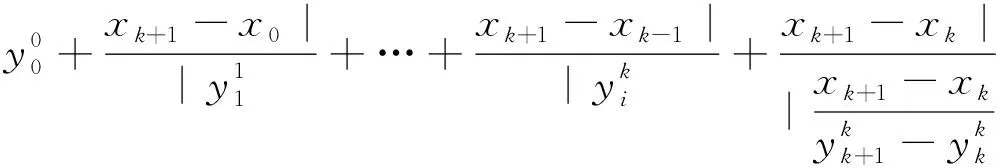
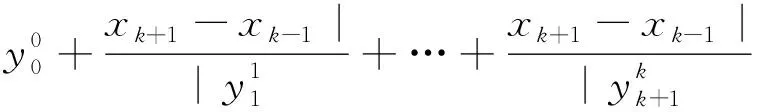
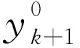
当n≥i≥k+2时，

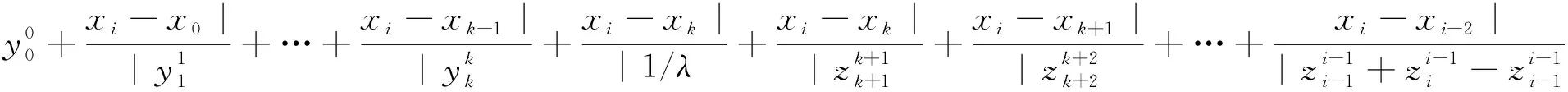
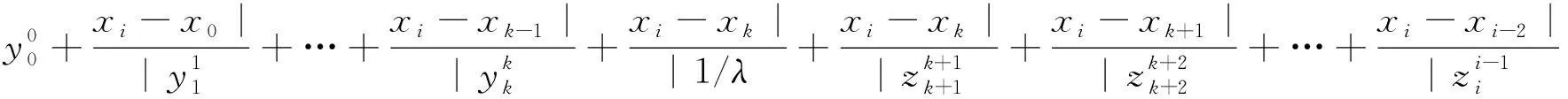
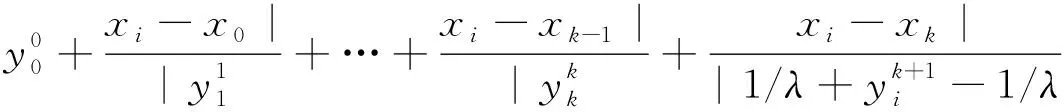
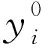
从反差商表3中可以看出，与原Thiele连分式有理插值式(5)相应的反差商表2相比较，两表中元素的上半部分(k+1行)和左半部分(k+2列)是相同的，即表3中含参数的反差商表仅仅是在反差商表2中增加了一行。不同之处在于第k+2行的增加，导致自第k+2行和第k+3行开始发生了变化，定理1的证明与原Thiele连分式有理插值定理的证明完全类似。这种构造含参数反差商的思路，不仅有助于学生打牢基础理论知识，激发学生的学习积极性，而且能培养学生除旧布新的创新意识和能力，求真务实的科学精神和严谨细致的工作作风。

1.4 含参数Newton插值多项式

类似于1.3节中的讨论，基于同样的构造思路可以得到含单参数的差商表如表4所示。

表4 含单参数差商表

考虑将原插值数据点中的任意一点(xk,yk),(k=0,1,…,n)作为一个二重结点，其它插值节点的重数保持不变。含参数Newton插值多项式可利用下列算法构造。

Step5：基于含参数差商表4和Step1—Step4中含参数差商式构造如下形式的含单参数的Newton型插值多项式[10]如式(12)所示。

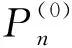
(12)

其中

下面定理2说明了构造的含参数Newton插值公式(12)是满足插值条件的。

定理2 对于给定的离散各节点互不相同的插值数据{(x0,y0),(x1,y1),…,(xn,yn)}，由(13)式所确定的Newton插值多项式函数满足插值条件如式(13)所示。

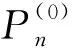
(13)

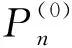
当i=k+1时，

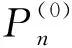
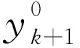
当n≥i≥k+2时，

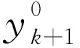
由于新构造的参数化Newton插值多项式和Thiele连分式插值中均含有参数，在插值数据给定的前提下，可以通过调节参数获得多个插值函数，使其在易于应用的同时便于理论研究。在不改变给定插值数据的前提下，在参数化Newton插值多项式和Thiele连分式插值函数中，选择合适的参数可以对插值区域内的任意点的函数值进行调整，进而修改曲线的形状，因此可将其应用于曲线设计，根据实际设计需要，自由地修改曲线形状，使之满足实际需要[9-10]。在实际教学过程中，这种在差商和反差商的构造过程中增加参数的思路学生易于接受，能培养学生用于探索的科研精神。

1.5 基于差商的插值法进一步拓展方法研究

在1.1-1.4节中，基于递归计算的差商方法，我们探讨构造了几种一元基于反差商和含参数的差商(反差商)的插值方法。事实上，基于1.1-1.4节中差商表的构造方法，我们可以继续引导学生对差商进行拓展，构造混合差商、关联差商、差商指、基于块的差商等多种新型差商，进而得到出多种一元混合有理插值公式[3,7-11]。此外，在实际应用中，多元插值出现较为普遍，因此在教学过程中，引导学生将二元插值看成先沿x方向的插值再沿y方向的插值，或者看成先沿y方向的插值再沿x方向的插值，基于上述各种扩展思路可以构造多种二元混合有理插值[3,8,11]。在实际教学过程中，我们还可以将标准的Hermite插值问题都归结到Newton插值公式上[12-13]，而且可以高效的解决问题。此外，在一些实际的插值问题中，如果已知的插值数据在一部分节点处给出了函数值和导数值，在另一部分节点处只给出了函数值，仍属于Hermite插值问题，一般称之为不完全Hermite插值或者间接Hermite插值或非标准Hermite插值问题。对于这种问题学者们给出一些求解方法，但都较为复杂，不利于理解。事实上，对于非标准Hermite插值[12-13]，我们可以通过引入参数构造重节点差商的方法，使非标准Hermite插值转化为标准Hermite插值进而求解。

构造法是一种技巧性很高的处理问题方法，可以化抽象为直观，化复杂为简单，加深学生对插值教学内容的理解和掌握。插值法拓展使用的构造法是计算思维中的一种经典的处理问题方法，核心是通过联想和划归的思想，根据题设条件的特征恰当构造一种新的方法来解决问题[14]。插值法公式特别多，学生学习掌握起来有一定的难度，为此，在教学实践过程中，通过引入构造法思想结合最新的插值理论科研成果，加深学生对教学内容的理解，激发学生的学习兴趣。在插值构造过程中让学生比较不同插值方法之间的区别与联系，学生能够较为容易的掌握大量繁琐公式。

2 数值例子

本节给出一个简单的数值例子说明第2节中几种基于差商的插值法拓展公式的有效性。

例.设给定一元插值数据如表5所示。

表5 插值数据

根据差商公式[2]可得差商表如表6所示。

表6 差商表

根据含参数差商公式(12)-(17)可得含单参数差商表如表7所示。

表7 含参数差商表

根据差商公式(2)-(4)可得反差商表如表8所示。

表8 反差商表

根据差商公式(6)-(10)可得含单参数反差商表如表9所示。

表9 含参数反差商表

由差商表6可得到Newton插值多项式，如式(14)所示。

(14)

由差商表7可得到含单参数Newton插值多项式，如式(15)所示。

(15)

易证P(xi)=P1(x) (i=0,1,2)。

由反差商表8可得到Thiele连分式有理插值，如式(16)所示。

(16)

由于r(x0)=r(2)=0≠1，(2,1)是一个不可达点。

利用文中1.3节算法，增加节点的重数，引入参数λ(λ≠0)，得到如表9所示的含单参数反差商表，可以得到参数化Thiele型连分式有理插值，如式(17)所示。

(17)

易证R2(xi)=fi(i=0,1,2)。

因此通过选择不同的参数λ，新构造的有理函数R2(x)总是满足插值条件。由于新构造的满足插值条件的Thiele连分式插值函数中均含有参数，R2(x)实际上是多个有理函数，如果我们选择λ=-1，则如式(18)所示。

(18)

如果我们选择λ=3，则如式(19)所示。

(19)

我们还可以选择其他的参数α，λ，参数化插值P1(x)和R2(x)可以变为其他的函数，方便在实际中使用。

3 结论

针对计算方法课程中Newton插值多项式方法的特点，本文对差商的几种改进方法从构造思路上进行拓展，研究探讨了构造法在插值理论教学实践中的应用，得到了Thiele有理插值、含参数Newton插值多项式和Thiele连分式有理插值方法。阐述了如何利用计算思维中的构造法思想培养学生的创新思维，提高学生解决实际问题的能力，形成和发展学生数学思维，提高插值与逼近法的教学质量。数值算例使学生更加深刻的理解插值构造过程，通过教学实践和最新的插值理论研究科研成果演示，基于构造法的插值理论拓展与教学方法有助于培养学生的创新和团结协作精神，训练学生科学思维方法，提升学生的创新思维和探索精神，激发学生科技报国的使命担当和家国情怀。