非粘结柔性立管螺旋键缠绕角度敏感性分析*
贾越钧, 郭海燕, 崔 鹏, 白永庆
(中国海洋大学工程学院, 山东 青岛 266100)
中国南海有巨大的油气资源,立管在海洋油气资源开发过程中的作用举足轻重,非粘结柔性立管具有比传统立管更小的弯曲刚度和更强的拉伸刚度,可产生较大变形来抵御外界荷载[1]。
非粘结柔性立管具有多层结构,每一层有各自的功能,各层之间通过装配联系在一起,共同承担整体荷载。其中,骨架层主要用于抵挡外压,防止立管在较大外压作用下压溃,防渗漏层主要保证管道内部油气的密闭性,抗压铠装层主要承受径向内外压力,防磨擦层铺设于金属层之间,一般为尼龙材料,减少金属层之间的磨损,抗拉铠装层提供轴向强度,由一对偶数条矩形截面的条形钢带缠绕而成,两层缠绕方向相反,铺设角度介于20°~55°之间[2]。各主要功能层的结构如图1所示。
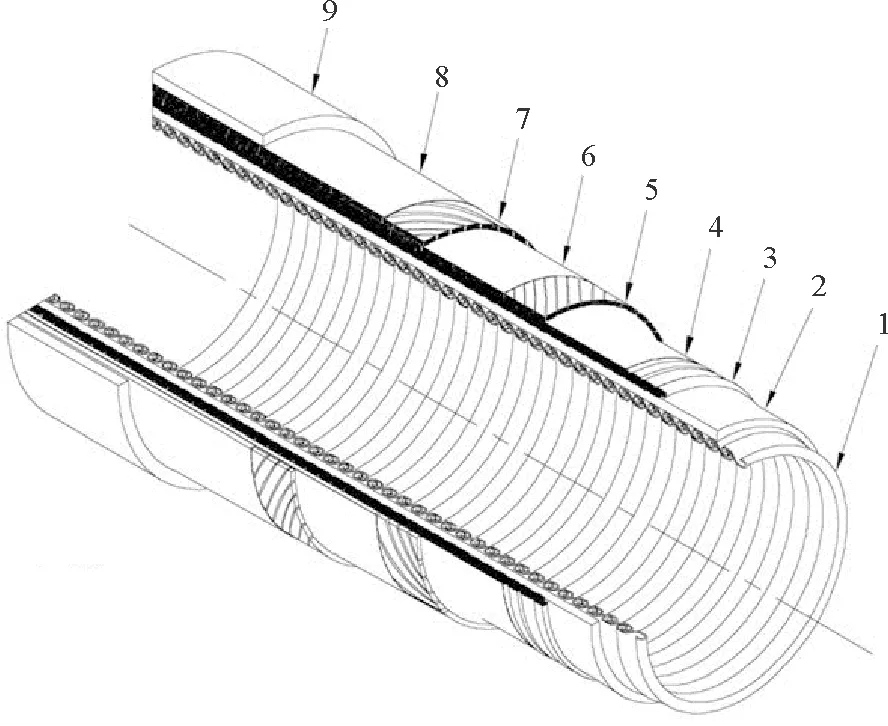
(1.骨架层 Carcass;2.内部防渗层 Polymeric barrier;3.抗压螺旋铠装层 Pressure armor;4.抗摩擦层 Anti-wear layer;5.拉伸铠装层 Inner tensile armor;6.抗摩擦层 Anti-wear layer;7.拉伸铠装层(反向) Outer tensile armor;8.抗鸟笼效应层 Insulating layer;9.外护套层 Outer sheath)
由于柔性立管的结构复杂,尤其是立管各层之间可以发生相对滑移,大量的非线性接触给柔性立管的局部分析带来了极大的困难,研究一般从理论方法,有限元方法和实验方法三部分展开。Feret与Roberto等[4-5]将柔性管的每一个层作为一个独立的部分进行研究,分析了螺旋条带的受力及变形情况,并建立了完全滑动和部分滑动两类模型,该模型考虑了立管各层间的接触应力以及层间间隙,但没有考虑轴力和弯矩等荷载的耦合以及层与层之间的摩擦力;Witz[6-7]将理论计算分析的结果与弯曲疲劳实验结果进行了对比分析,并对6.35 cm柔性管的拉伸、扭转和弯曲性能进行了循环荷载实验;Kebadze和Kraincanic[8]采用Coulomb摩擦理论来分析层间摩擦行为,假设层间发生的滑动为轴向滑动,忽略了螺旋构件的扭转和弯曲刚度,研究了柔性管的非线性弯曲行为;de Sousa等[9]利用ANSYS建立了三维有限元模型分析安装过程中柔性管道的结构响应。Bahtui等[10-12]运用Abaqus建立了一个五层非粘结柔性管模型和六层非粘结柔性管结构,模拟了其在拉伸、扭转和弯曲载荷作用下的响应。
综上可知,理论分析的方法往往都是忽略摩擦效应,但层间的滑移摩擦却是导致非粘结柔性立管非线性本构关系的重要原因。由于实验研究对设备、造价等要求苛刻,因此大部分的研究采用有限元分析研究,有限元分析的难点在于如何处理层与层之间的摩擦接触,保证结果收敛,并提高计算效率。立管中抗拉铠装层是立管承受拉伸、扭转荷载的主要受力构件,大量的有限元研究和实验研究中,目前鲜有将螺旋键缠绕角度作为唯一变量,研究其对立管整体力学性能的影响。
本文运用等效刚度法将截面复杂的骨架层和抗压螺旋铠装层简化为矩形截面的正交各向异性壳结构,将防渗漏层、抗磨擦层等简化为各项同性的连续面层,用Line单元来模拟两层螺旋方向相反的螺旋抗拉铠装层,赋予每条Line单元实际螺线条带的形状,将整个模型简化为梁—壳组合模型,考虑层与层之间的摩擦和接触。,建立五种不同铺设角度螺旋键的8层非粘结柔性立管简化模型,分别为25°、30°、35°、45°和55°,通过与立管原型分析对比,验证简化模型的准确性,分析其在内压和拉伸、扭转、弯曲的组合荷载工况下截面的力学性能,探究螺旋键缠绕角度对柔性立管的力学性能的影响,为非粘结柔性立管结构的详细设计和分析提供技术参考。
1 非粘结柔性立管简化模型
1.1 骨架层的简化数值模拟
如何将骨架层和抗压铠装层简化为等效矩形截面的正交各向异性壳结构,以及如何确定简化后的等效材料参数是柔性立管简化的关键部分。本节采用等效刚度思想,求得材料各项等效参数。下面以非粘结柔性立管的骨架层为例,计算简化骨架层的正交各向材料参数。
骨架层:由类似S型截面的钢带以接近90°的缠绕角度螺旋缠绕,相互扣锁而成,主要用于抵抗外部压力,防止外压过大导致结构压溃,材料一般为不锈钢(见图2)。

图2 骨架层剖面
骨架层的力学性能很像连续的正交各向异性的圆柱壳,因此将这类结构层等效简化为正交各向异性壳。所以此类材料需要给出9个独立参数,分别是三个主轴方向的弹性模量EZ、ER、ET,三个主轴方向剪切弹性模量GZ、GR、GT,以及三个泊松比。首先建立一个柱坐标系,沿管道轴向为T轴,管道径向为R轴,沿管道周向为Z轴。
(1)Z轴等效参数的确定
根据Timoshenko 和Woinowsky-Krieger[13]和Gilberto等[14]的等效刚度思想,可以得到周向Z的弹性模量EZ,剪切模量GZ,根据Neto等[15]提出的修正后的单位长度等效刚度法求得等效厚度ts。
(1)
(2)
(3)
其中,Ec、Gc分别是骨架层的弹性模量和剪切弹性模量,Ec=190 GPa,Gc=Ec/2(1+vc);Ib表示骨架层的切向惯性矩;Ac表示骨架层的截面面积;It表示骨架层的扭转惯性矩;泊松比vc为0.3;L的计算方式:
(4)
(2)R轴等效参数确定
骨架层主要承受压力荷载,只对其受压状态探讨,当受到径向压力时,可以把等效区域内ab,a′b′两杆视为承载部位,其余结构不受力(见图3)。
径向弹性模量ER:
(4)
剪切模量GR:我们假定等效前后的结构具有相同的剪应变:
(5)
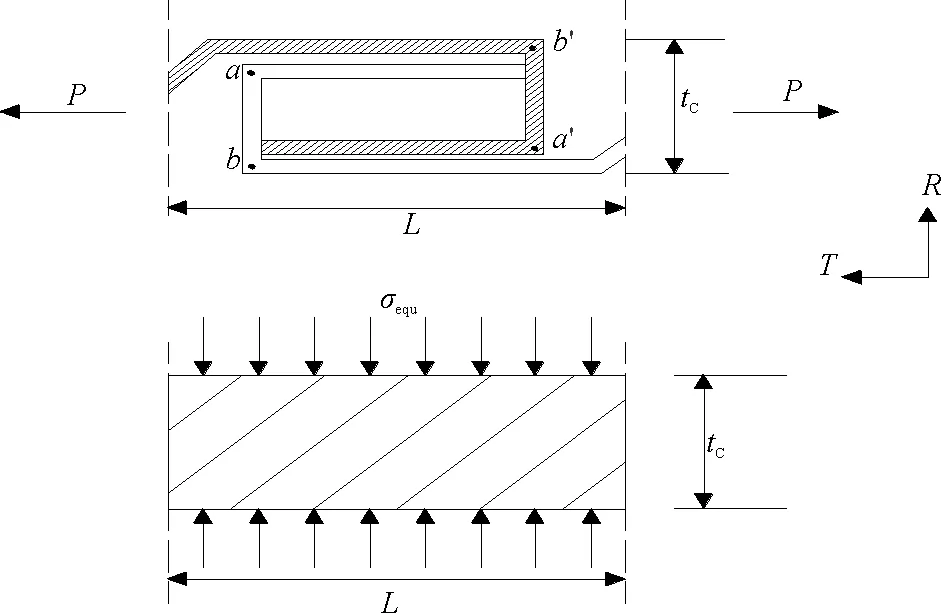
图3 骨架层等效前后沿R轴荷载图
(6)
则有γ=γ′可知
(7)
(3)T轴等效参数的确定
根据文献[16],使等效结构与被等效结构在相同荷载作用下位移响应相同。如图4所示,上部是骨架层受荷载P作用,下图是受到均布荷载P/t作用。且取μT=0.000 17[17],则
(8)
根据Gc=Ec/2(1+vc)可得出剪切弹性模量GT。
抗压铠装层简化数值模拟也可按照上述方法计算得到。

图4 骨架层等效前后沿T轴荷载图
1.2 非粘结柔性立管总体简化模型
非粘结柔性立管有限元简化模型见图5,本文采用的立管参数,来自国际船舶与海洋工程结构大会(ISSC)分别对63.5 mm的非粘结柔性管的拉伸刚度、弯曲刚度和扭转刚度进行了实验研究的参数[12]。实验证明,非粘结柔性立管局部力学性能的试样长度一般选取在 2~4 倍的立管外层螺旋铠装层的螺距长度,取此长度作为试验试样长度可以有效地模拟立管的力学性能,本文取柔性立管长度1 400 mm。
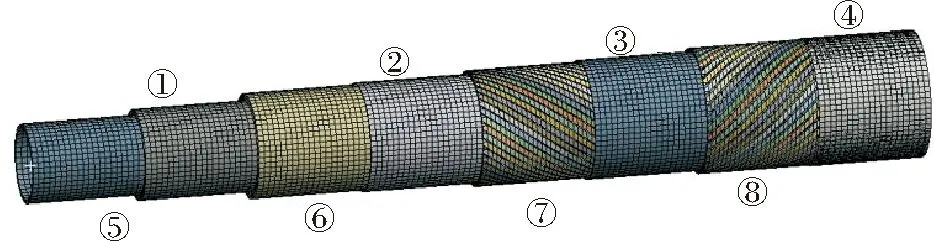
(①内部防渗层 Polymeric barrier;②抗摩擦层 Anti-wear layer;③抗摩擦层 Anti-wear layer;④外护套层 Outer sheath;⑤简化骨架层 Simplified carcass;⑥简化抗压铠装层 Simplified pressure armor;⑦抗拉螺旋铠装层 Inner tensile armor;⑧抗拉螺旋铠装层(逆时针) Outer tensile armor)
分别建立25°、30°、35°、45°、50°抗拉铠装层的整体简化模型,除抗拉铠装层角度不同以外,其余各项尺寸、材料参数均相同。其具体尺寸参见文献[11]。
模型中骨架层与抗压螺旋铠装层这两层螺旋角度大,而且螺旋键为自锁结构,其力学性能很像连续的正交各向异性的圆柱壳,因此将这类结构层等效简化为正交各向异性壳。
抗拉螺旋铠装层由众多螺旋角较小的螺旋矩形条带,角度为20°~55°[2],由于螺旋键之间非粘结,其间只有相互挤压的时候才对彼此造成接触压力,而彼此相离时之间并无相互作用,因此需要用详细模型建立以模拟其真实的力学响应。这类结构层考虑到单个螺旋键的力学性能与曲梁类似,可以将其建立为梁单元,以一定角度螺旋缠绕在内部核心圆柱体结构上。顺时针抗拉铠装层和逆时针抗拉铠装层的键数分别为 44 和 40。本文一共建立不同螺旋角度的柔性立管有限元模型,分别为25°、30°、35°、45°和55°共五个简化模型,不同模型除角度不同外,其余结构与参数均相同。
防渗漏层、抗磨擦层以及外护套层为各项同性的连续面层,这类结构材料均为各项同性,其厚度远小于直径,可以当作同心圆柱壳来建立。基于以上所述的等效方法,便可将非粘结柔性立管的模型便可以等效为梁—壳组合模型。
1.3 层间接触与摩擦
ANSYS提供多种接触算法,有罚函数法、多点约束法(MPC)、扩展拉格朗日算法、拉格朗日乘子法等。本文采用扩展拉格朗日算法,该算法是将罚函数与纯拉格朗日乘子法结合起来,迭代开始时采用罚函数法,达到平衡检查侵入容差,当不满足时则通过拉格朗日乘子法修正接触刚度继续迭代以满足侵入容差要求,具有较高的收敛保证性。本文利用有限元模型中的contact 和target单元模拟层间的接触变形,以确保计算的收敛性。此外,利用典型库伦摩擦模型模拟层间的摩擦和滑移,设置摩擦系数为0.1,保证了加载过程中层间的真实受力和变形情况。
1.4 约束与荷载
本文中不同螺旋键角度的模型所施加的荷载均为表1所示。
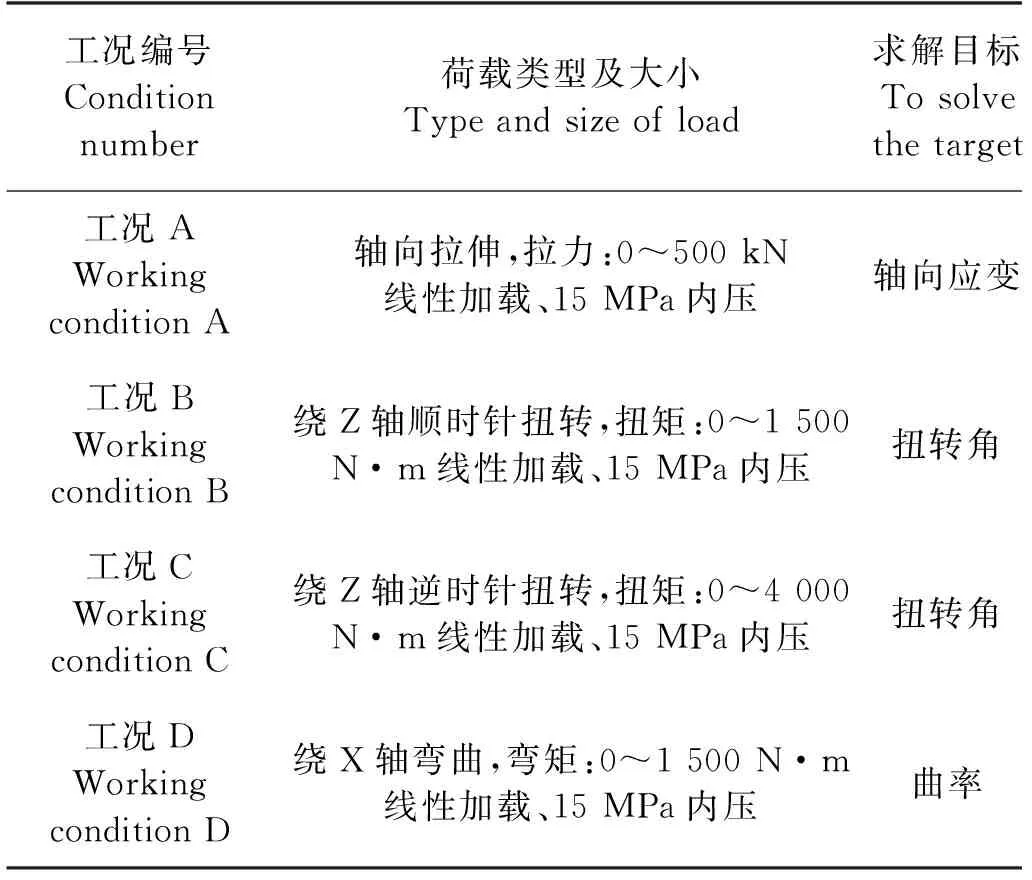
表1 荷载工况
非粘结柔性立管在深海中传输的是高温高压的油气,因此在研究柔性立管局部力学性能时,加入内压荷载将会更加贴近实际,也是非常有必要的,本文在简化柔性立管模型的基础上,分别讨论在有15 MPa内压荷载[18]作用下的不同螺旋键角度的柔性立管的拉伸,扭转和弯曲力学性能。
立管一端施加固定约束,限制平动和转动,另一端施加荷载,为方便施加荷载,在模型中建立一个直径略大于立管直径的厚度10 mm钢材料圆盘,立管端部与进行圆盘实体的内侧面点—面、线—面绑定接触,这样可在圆盘外侧面上施加荷载,将荷载传送到立管受力端,使柔性立管受力端均匀承受荷载,这种做法方便拉伸、弯曲与扭转荷载的施加,可模拟力直接施加在立管端部效果相同。
2 非粘结柔性立管实体模型与简化模型对比
本章共采用两类模型,为了不使概念混淆,现对两类模型做如下定义:
实体模型:按骨架层和抗压铠装层实际截面形状建模
简化模型:按骨架层和抗压铠装层简化后的圆柱壳形状进行建模
2.1 骨架层与抗压铠装层简化模型验证
为验证简化骨架层、简化抗压铠装层的材料性能和受力反应是否与骨架层原型、抗压铠装层原型相同,建立了如下骨架层和抗压铠装层实际截面形状的有限元模型,采用的骨架层与抗压铠装层参数,源自国际船舶与海洋工程结构大会(ISSC)分别对63.5 mm的非粘结柔性管的拉伸刚度、弯曲刚度和扭转刚度进行了实验研究的参数[12]。长度为700 mm,对比骨架层原型和简化骨架层、抗压铠装层原型与简化抗压铠装层在相同拉伸、扭转与弯曲荷载下的结构变形与刚度,进而验证简化骨架层和简化抗压铠装层的力学性能是否能够真实反映非粘结柔性立管中的骨架层与抗压铠装层(见图6、7)。

图6 骨架层有限元模型图

图7 抗压铠装层有限元模型图
骨架层所加约束与荷载除无内压之外与1.4节中相同;抗压铠装层因截面不同,所以单独承受荷载能力比整体小很多,因此所加荷载相应减少,所加约束与荷载如表2所示。
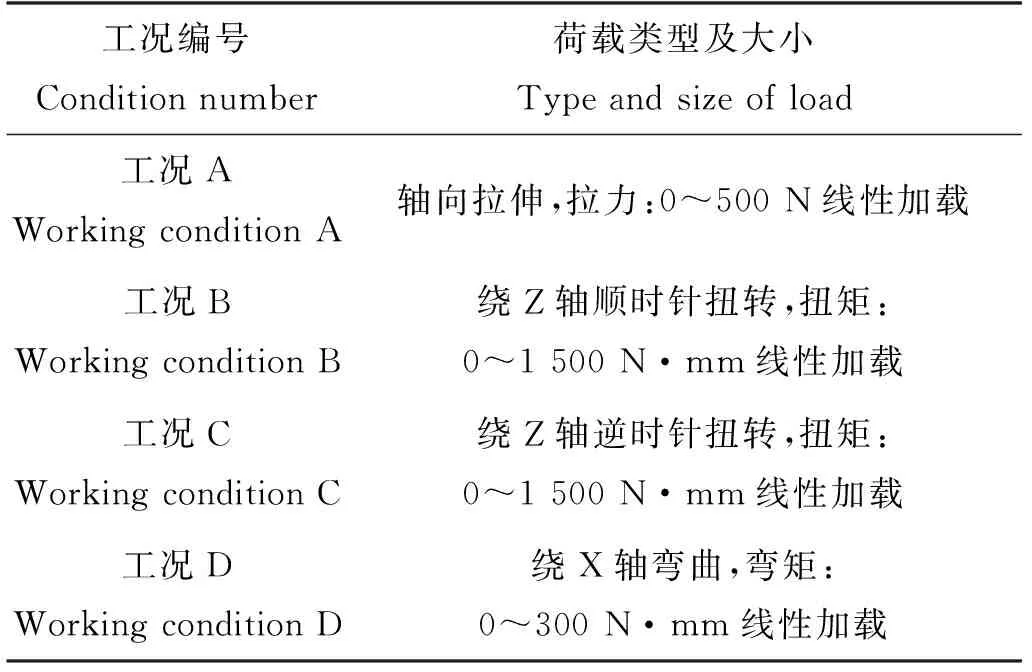
表2 抗压铠装层施加荷载工况
由上述计算可以看出,四种荷载作用下,真实骨架层总变形与简化骨架层总变形相近,因此可以验证简化后的骨架层拉伸刚度、扭转刚度等材料特性与结构受力反应与真实骨架层相似。真实抗压铠装层与简化抗压铠装层总变形在工况D作用下相近,在其他工况下总变形有所差异。将简化骨架层与抗压铠装层代入简化柔性立管整体模型中,加入层间接触与摩擦,与立管实体模型进行对比。
2.2 立管实体模型与简化模型对比
实体模型采用的立管参数,与简化模型相同,源自国际船舶与海洋工程结构大会(ISSC)分别对63.5 mm的非粘结柔性管的拉伸刚度、弯曲刚度和扭转刚度进行了实验研究的立管参数,抗拉螺旋铠装层螺旋角度为35°,荷载与1.4节相同,立管模型如图8所示。
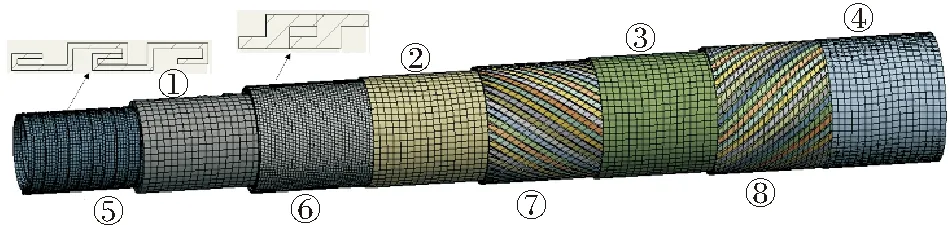
(①内部防渗层 Polymeric barrier;②抗摩擦层 Anti-wear layer;③抗摩擦层 Anti-wear layer;④外护套层 Outer sheath;⑤骨架层 Carcass;⑥抗压铠装层 Pressure armor;⑦抗拉螺旋铠装层 Inner tensile armor;⑧抗拉螺旋铠装层(逆时针) Outer tensile armor)
柔性立管有限元实体模型节点数为1 413 575个,单元数为384 267个,简化模型节点数为45 442个,单元数为39 513个。简化模型使计算效率大大提高。
层间接触、摩擦系数以及约束和荷载都与第一节简化模型分析相同,四种工况作用下模型计算结果如表4所示。
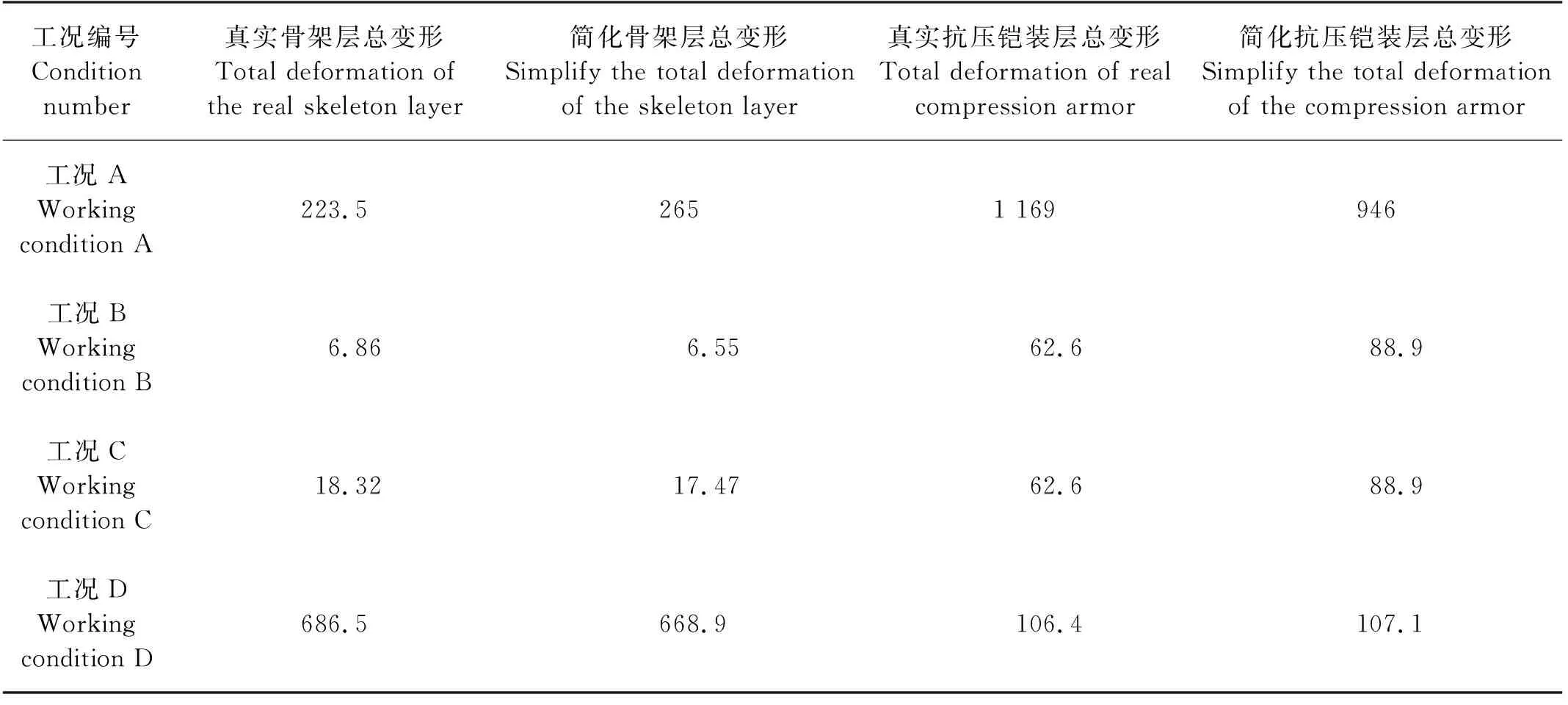
表3 骨架层与抗压铠装层不同工况变形对比
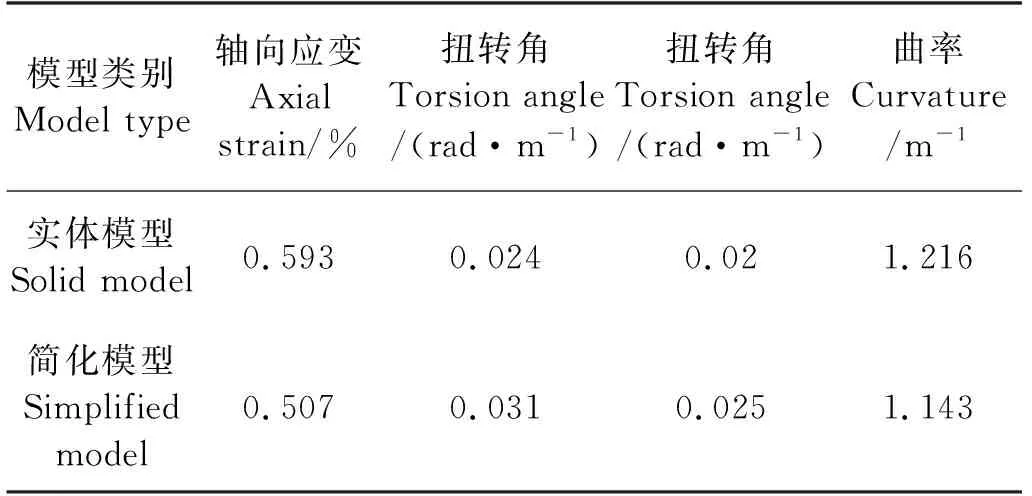
表4 实体模型与简化模型变形对比
由上述计算可以看出,四种荷载作用下,整体实体模型与简化模型力学性能相似,误差在可接受范围内,因此可以验证简化模型的拉伸刚度、扭转刚度等材料特性与结构受力反应与实体模型相似,可以用简化模型进行不同螺旋角度的敏感性分析,即能节省计算时间,又能保证计算精度。
3 有限元模型计算分析
3.1 不同角度柔性立管轴向拉伸刚度对比
不同抗拉螺旋键角度简化模型在工况A(不同内压)作用下求解结果对比见图9。
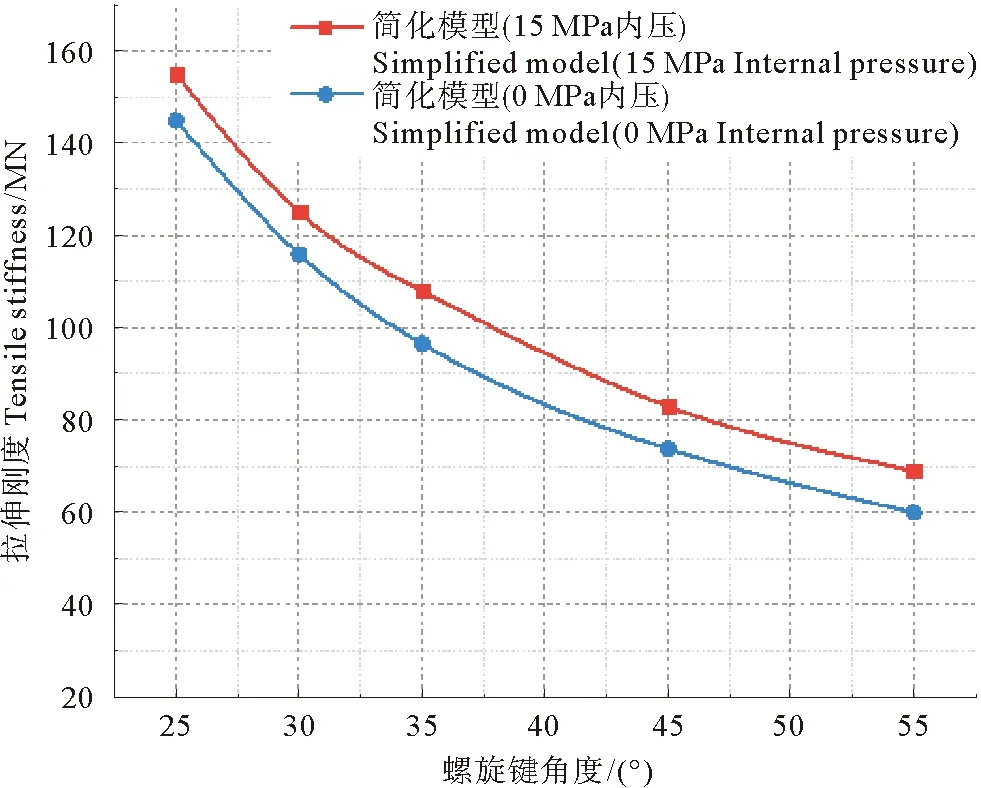
图9 轴向拉伸刚度对比
由图9可知,随着抗拉铠装层螺旋键角度的增大,立管整体的抗拉刚度呈下降趋势。在内压的作用下,相同角度的柔性立管的轴向抗拉刚度变大,这是由于在内压作用下,增大了层与层之间的摩擦力,从而增加了抵御外部荷载的能力,使得柔性立管的拉伸刚度增强。且由上图可以看出,内压虽对抗拉刚度的提高有利,但是对抗拉刚度的提高程度较小。25°与30°螺旋键立管抗拉刚度提升比35°、45°与55°小相同角度差异下,25°到35°之间的轴向拉伸刚度下降的较快,35°到55°之间拉伸刚度下降趋势变缓。
3.2 不同角度柔性立管扭转刚度对比
不同抗拉螺旋键角度简化模型在扭转工况(不同内压)作用下立管扭转角度求解结果对比见图10。
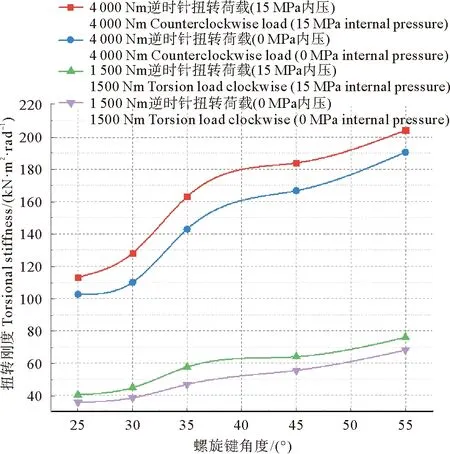
图10 扭转刚度对比
由图10可以明显看出,首先随着抗拉铠装层螺旋键缠绕角度变大,立管的扭转刚度是逐渐增加的,因此我们可以得出,立管的扭转刚度与螺旋键缠绕角度成正比。且在25°~35°这一段扭转刚度增加较快,而从35°~55°过程中,扭转刚度增加变缓。
这是因为螺旋钢带缠绕在抗磨擦层上,管道两端的扭矩荷载作用在螺旋钢带上时,可以视为在螺旋钢带的一微段上作用了一个集中力,将此集中力分解为沿螺旋钢带方向的力T1和垂直于螺旋钢带的力T2,当螺旋钢带角度较小时,T2所占集中力的分量大于T1,螺旋钢带垂向承担的荷载较大,所以扭转变形较大,随着螺旋钢带的缠绕角度不断增大,T1的所分得的作用了不断增大,螺旋钢带轴向承担的荷载渐渐变多,扭转变形越来越小,因此扭转刚度不断变大。同时,通过公式可知,立管的拉伸刚度越大,在相同螺旋角度下,立管的扭转刚度也会增大,随着螺旋角度的逐渐增大,立管的抗拉刚度是逐渐减小的,所以受此影响,虽然随螺旋角度增大扭转角度不断变小,但是扭转角度的下降曲线是逐渐放缓的。
其次,逆时针作用下的扭转刚度要大于顺时针工况下的立管扭转刚度,这是因为顺时针作用方向与最外层抗拉螺旋铠装层的螺旋键缠绕方向相反,最外层螺旋键半径要比内侧的大,当工况B施加在管道端部时,螺旋条带随着加载逐渐增大,会渐渐与内部的抗磨擦层分离,减小了层间最大静摩擦力,造成的变形较大,因此降低立管整体的扭转刚度,严重时会造成鸟笼效应,因此在选择工况B时,所加荷载较小。而顺时针工况C作用方向与最外层螺旋键缠绕方向相同,当工况C施加在管道端部时,螺旋条带随着加载逐渐增大,渐渐与内部抗磨擦层压紧,使层间最大静摩擦力增大,层间位移不容易发生,因此可以承受较大荷载,相同荷载大小下,顺时针扭转荷载比逆时针荷载造成的扭转角度更小,扭转刚度更大。
第三,内压作用下,层与层之间压力增大,最大静摩擦力也会增大,因此会增加柔性立管的扭转刚度,但是对扭转刚度有较小程度增加。
3.3 不同角度柔性立管弯曲刚度对比
不同抗拉螺旋键角度的立管简化模型在工况D(不同内压)作用下曲率求解结果对比见图11。

图11 弯曲刚度对比
由图11中可以看出,第一,抗拉铠装层的螺旋角度与弯曲刚度成负相关,螺旋角度越大,立管的抗弯能力越弱,但是抗弯刚度的差距并不是很明显,螺旋角度的变化对抗弯刚度的影响比较弱。第二,内压对立管弯曲刚度的影响比较大,这是因为弯曲使得立管的曲率发生变化,使得层间发生滑移,而施加内压之后,增大了层间的摩擦力,若使层间发生滑移则需要施加更大的荷载,因此在内压作用下立管层与层之间的粘滞状态延长,因此可以有效增加立管的弯曲刚度,承受更大荷载。以上结果都是在弯曲荷载较小的作用下产生的,因此立管各层之间处于粘合状态,未发生相对滑移。
4 结论
建立了深海非粘结柔性立管有限元实体模型与有限元简化模型,将简化与未简化的柔性立管中的骨架层和抗压铠装层在同工况下对比,再将简化和未简化的整体柔性立管模型在同工况下对比,验证了简化模型的合理性与准确性。建立不同抗拉铠装层螺旋角度的立管简化模型,在内压作用下求出各自的拉伸刚度、扭转刚度、弯曲刚度进行对比分析,探讨不同螺旋条带角度的立管在相同荷载下的力学性能与敏感性关系,得出以下结论:
(1)简化模型的计算结果与未简化模型结果达到了比较高的相似度,与柔性立管的本身的力学性能贴合,并且简化模型的单元节点数远小于实体模型,所需的计算时间远小于实体模型,因此可以提高计算分析的效率。
(2)随着抗拉铠装层螺旋键角度的增大,立管的抗拉刚度变小,且在内压的作用下,相同角度的柔性立管的轴向抗拉刚度变大,这是由于在内压作用下,增大了层与层之间的摩擦力,从而增加了抵御外部荷载的能力,使得柔性立管的拉伸刚度增强。
(3)随着抗拉铠装层螺旋键缠绕角度变大,立管的扭转刚度是逐渐增加的;逆时针作用下的扭转刚度要大于顺时针工况下的立管扭转刚度,这是因为最外层抗拉螺旋铠装层的螺旋键缠绕方向也是逆时针,且最外层螺旋键半径要比内侧的大。
(4)随着抗拉铠装层螺旋键缠绕角度变大,立管的弯曲刚度逐渐减小,螺旋角度的变化对抗弯刚度的影响比较弱,内压对立管弯曲刚度的影响比较大,这是因为弯曲使得立管的曲率发生变化,使得层间发生滑移,而施加内压之后,增大了层间的摩擦力,所以增大了立管的弯曲刚度。
(5)内压的施加对结构的刚度是有利的,会导致三个刚度的增加,非粘结柔性立管受到内压荷载会增大层间的摩擦力,摩擦力是阻碍层间滑移的重要因素,所以内压的增加会导致刚度增加,在这三个刚度之间,内压对于弯曲刚度的增加是比较明显的,而对于拉伸刚度和扭转刚度有较小程度的增加。

