基于非线性能量阱的随机波浪载荷下导管架海洋平台的振动控制*

郑中强， 姚志鹏， 常宗瑜，2

(1. 中国海洋大学工程学院， 山东 青岛 266100； 2. 山东省海洋工程重点实验室， 山东 青岛 266100)

工作在复杂海洋环境下的海洋平台受到风、浪、流、地震等载荷的作用，会产生持续的水平振动，影响海洋平台的使用寿命和平台上工作人员的安全。随着对海上能源需求的增加，海洋平台越来越多的被应用于海上油气资源的开发，减小平台的振动日趋重要。

通过线性动力吸振器被动吸收平台的振动已经得到广泛的研究，其中调谐质量阻尼器(Tuned Mass Damper，TMD)应用较多。Li等[1]针对海洋平台在随机波浪载荷下的振动，通过控制位移标准差的最大减小量，得到了TMD的优化设计方法，并分析了不同波浪参数对TMD最优参数的影响。Wang等[2]研究了海洋平台在冲击载荷作用下的振动控制问题，从能量传递与耗散的角度对TMD的参数进行了优化设计。Yue等[3]研究了海洋平台在受冰激载荷时的振动响应，分析了最优参数的TMD并应用到海洋平台上，结果表明TMD可有效控制冰激激励下海洋平台产生的振动。嵇春艳[4]通过模态分析的方法，研究了TMD对海洋平台不同模态的减振效果，结果表明TMD只对单一模态的振动有较好的控制效果。然而，TMD的频率鲁棒性较差，一旦TMD的固有频率与主系统的固有频率发生偏离，其振动控制效果会显著降低[5]。所处恶劣环境中的海洋平台等结构很容易发生破损、腐蚀，在平台上安装各种设备导致质量增加，这些影响可能使结构的固有频率发生变化。因此，必须寻找新的方法以克服TMD减振频带窄的缺点。

非线性能量阱(Nonlinear Energy Sink，NES)作为一种新型被动非线性动力吸振器，其在传统的线性动力吸振器中引入非线性刚度，使得NES没有固定的频率，能够保证NES在较宽的频带上与主结构发生共振，到达较好的振动抑制效率。通过适当的参数设计，使主结构与NES之间发生靶能量传递将主结构中的振动能量传递到NES中，并由NES中的阻尼耗散。Vakakis[6]研究了附加有NES的线性振子在脉冲激励下系统能量传递的问题，发现了NES能量定向传递的特性，经过适当的设计NES可作为被动减振器使用。Gourdon等[7]通过实验验证了NES的能量定向传递，并表明NES在结构固有频率发生变化后依然有效。Lu等[8]提出一种轨道型NES与钢框架相结合，建立了其数学模型，通过分析不同激励下钢框架的位移响应，验证了NES宽频带的振动控制特性，并研究了不同阻尼对振动控制效果的影响。Georgiades等[9]研究了线性简支梁附着NES后的振动抑制和能量传递的问题，并通过数值模拟的方法优化了NES的参数和安装位置。Ahmadabadi等[10]和Fang等[11]分别将NES与压电材料和磁致伸缩材料相结合，减小主结构振动的同时收集传递到NES中的振动能量，并且从能量收集的角度对NES的参数进行了优化。Dai等[12]研究了NES对圆柱涡激振动抑制效果，通过对系统数学模型进行无量纲化后，分析了NES的无量纲阻尼、刚度和质量对涡激振动抑制效果的影响，并优化了NES的参数。李爽等[13]研究了不同的冲击激励下NES对主结构的振动抑制效果，结果表明当冲击能量超过一定临界阈值时，会激发靶能量传递达到较好的振动抑制效果。陈勇等[14]研究了NES对高耸结构的振动抑制效果，将高耸结构简化为悬臂梁，通过数值分析表明 NES 可有效吸收结构振动，并给出了NES参数的选择方法。Kremer等[15]提出一种带有永磁体的NES，实现振动控制和能量获取，建立了系统的数学模型，对装置在瞬态响应下的吸振和能量采集性能进行了仿真研究，结果表明该系统具有良好的能量定位能力和宽频带的减振能力。Wang等[16]研究了轨道NES对建筑物的振动控制效果，主要针对建筑结构物受到外部因素导致自身刚度发生变化时，对比研究了轨道NES、立方刚度NES和TMD之间减振效果的差异，结果表明NES对结构刚度变化更具有鲁棒性。Wierschem等[17]对在地震载荷下NES和TMD的减振性能进行了对比，研究结果表明，在建筑结构固有频率不变的情况下，TMD的性能较好，当固有频率发生变化时，NES系统在控制结构响应方面表现出较好的性能。

本文通过建立海洋平台耦合NES系统动力学模型，根据谱分析法模拟随机波浪载荷，从降低平台位移响应均方差的角度对随机波浪载荷作用下NES进行了优化设计，对比分析了NES与TMD的振动控制性能，通过瞬时能量传递和位移响应小波变化分析了NES的振动控制机理。

1 系统动力学模型

海洋平台的结构和所处环境较为复杂，本文仅取海洋平台的第一模态，将系统看作为单自由度系统(SDOF)，这是因为系统第一模态的响应对结构来说最为主要，振动危害主要发生在第一模态上。本文以一导管架平台[18]为例，通过数值计算分析NES对海洋平台的振动控制效果，平台具体参数见表1。建立NES—海洋平台简化模型,见图1。

表1 海洋平台主要参数

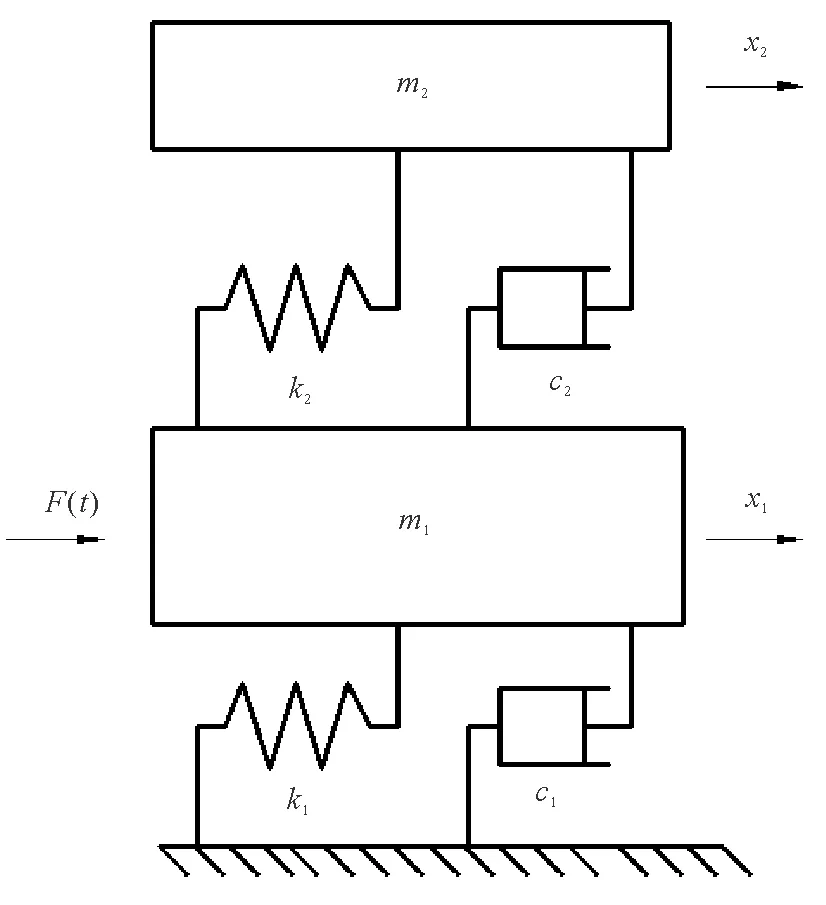
图1 NES—海洋平台系统结构模型

系统的动力学方程可表示为：

(1)

式中：m1、c1、k1分别表示海洋平台的质量、阻尼和刚度；m2、c2、k2分别表示NES的质量、阻尼和刚度；x1、x2分别表示海洋平台与NES的位移；F(t)表示作用于海洋平台上的随机波浪载荷。

2 随机波浪载荷

本文通过谱分析法模拟随机波浪载荷。选用改进后的JONSWAP谱描述不规则波：

Sη(ω)=

(2)

式中：

Hs为有效波高(m)；T为峰值周期(s)；γ为谱峰升高因子(均值为3.3)；σ为峰形系数，其取值为：

ω≤ωm,σ=0.07；

ω≥ωm,σ=0.09。

海浪的波面可以看作一个平稳随机过程，它是由多个不同周期不同随机初相位的余弦波叠加而成，即得海浪的波面：

(3)

作用在张力腿上的随机波浪载荷F(t)可由Morison方程计算得到：

(4)

式中：cD为Morison方程拖曳力系数，cD=1.4；ρ为海水的密度，取ρ=1 025 kg/m3；D为张力腿直径；cM为Morison方程惯性力系数，cM=2。

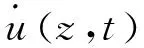
(5)

式中：g为重力加速度；k为波数；d为平台工作水深。

取波浪参数Hs=8 m，T=10 s。计算得到图2 所示的JONSWAP波浪谱, 图3作用于平台上的随机波浪载荷F(t)。

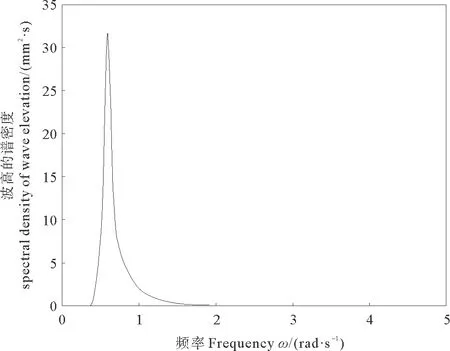
图2 JONSWAP波浪谱

图3 随机波浪载荷

3 导管架平台的振动控制系统

3.1 基于NES的振动控制

由于海洋平台所受到的载荷为随机波浪载荷，其响应也是一个零均值的平稳随机过程，所以本文通过平台第一模态位移响应的均方差来衡量海洋平台产生振动的剧烈程度。通过式(6)表示海洋平台位移响应的均方差：

(6)

式中μ表示位移响应的平均值。

本文以海洋平台有无NES时位移均方差的变化量作为反应NES对海洋平台振动控制效果的标准，其可表示为：

(7)

式中：δ0表示平台未安装NES时的位移响应均方差；δn表示平台安装NES后的位移响应均方差。

在对NES参数进行优化时，首先确定其质量大小为平台质量的5%。确定质量后，NES需要优化的参数为非线性刚度和线性阻尼。通过龙格-库塔法计算海洋平台在随机波浪载荷下的位移响应，得到海洋平台位移响应的均方差，以最大均方差减小量J=max(φ)为目标函数,在非线性刚度k2=3.283 2×106～1.969 9×108N·m-3，线性阻尼c2=6.411 5×102～1.282 3×106N·s·m-1范围内进行寻优求解，得到均方差减小量最大值max(φ)所对应的k2和c2的值即为最优非线性刚度和最优线性阻尼。参数变化对应的减振效果如图4可见，根据优化结果选取NES的非线性刚度为k2=2.955×107N·m-3，线性阻尼为c2=4.424×105N·s·m-1，质量为m2=391 270 kg。

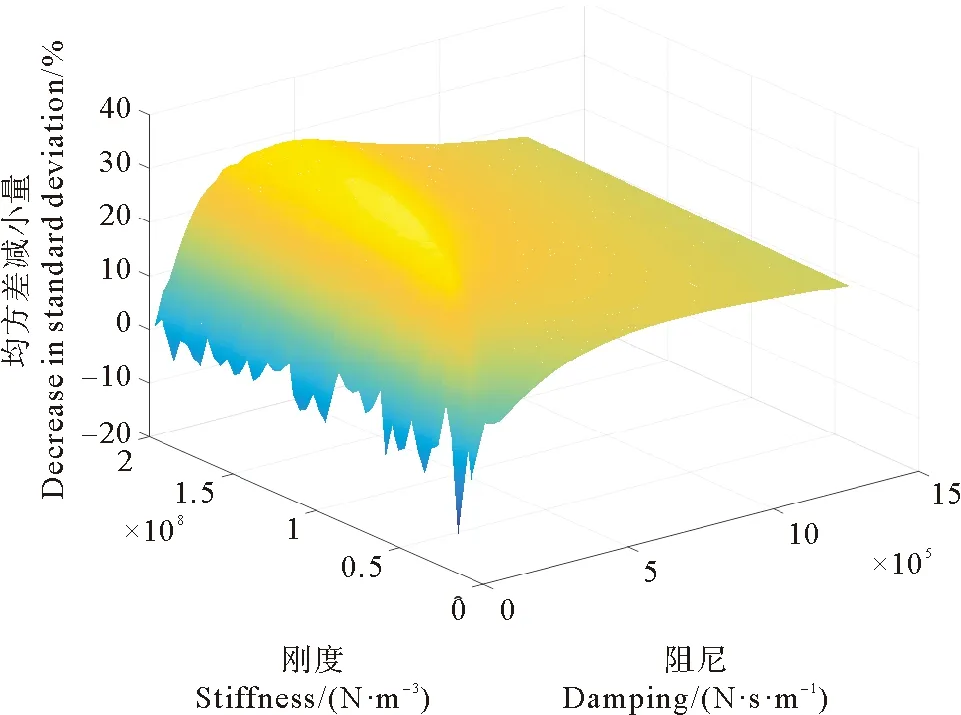
图4 不同NES参数下平台的振动控制效果

3.2 基于TMD的振动控制

TMD选取与NES相同的质量，仍为平台质量的5%，TMD的刚度和阻尼通过动力减振器的经验公式来确定最优值。具体设计公式为：

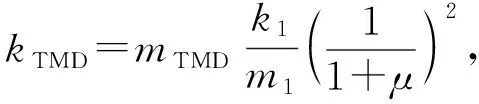
(8)

根据经验公式计算可得TMD的线性刚度为kTMD=1.489×106N·m-3，线性阻尼为cTMD=2.04×105N·s·m-1，质量为mTMD=391 270 kg。

4 NES的振动控制分析

4.1 NES振动控制性能分析

首先对附加质量锁定的锁定系统、NES系统和TMD系统在随机波浪载荷作用下的平台位移进行分析。考虑平台工作环境恶劣，长期工作受到腐蚀、强震、强风等作用可能导致结构刚度、频率等特性发生变化，分别分析了平台结构刚度不变即为100%时和结构刚度下降为理论设计值的45%时不同控制系统下平台的位移响应。

由图5可知，当平台结构刚度为100%时NES系统的振动控制性能虽然差于TMD系统的控制效果，但NES系统也能保持良好的减振效果，位移峰值始终低于锁定系统。由图6可知，当平台结构刚度退化为原刚度的45%后，TMD系统的振动控制性能明显下降，部分时间的位移峰值甚至超过锁定系统，这是因为平台结构刚度变化后导致自身频率发生变化导致TMD与平台失去调谐，使TMD的减振效果大幅下降。而NES系统依旧可以保持原有的振动控制性能，减振效果并未发生明显的退化。

((a)平台的位移响应;(b)位移响应局部放大图。(a) Displacement response of the platform; (b) Locally enlarged view of displacement response.)

((a)平台的位移响应;(b)位移响应局部放大图。(a) Displacement response of the platform; (b) Locally enlarged view of displacement response.)

针对以上现象，继续探讨平台结构刚度在原设计刚度的30%～130%变化时不同系统的振动控制效果，用以分析不同控制系统刚度的鲁棒性。图7给出了平台结构刚度变化时NES系统和TMD系统与锁定系统的平台位移均方差比值，比值越小说明振动控制效果越优，可以看出NES系统与锁定系统的均方差比值在整个刚度变化范围内处于0.89～0.75之间这说明在平台结构刚度发生变化时NES始终保持一定的振动控制效果，其振动控制性能受平台结构刚度变化影响不大。TMD系统在平台结构刚度变化不大的共振区域内可达到优于NES的振动控制效果，但随着平台结构刚度的变化TMD逐渐失谐振动控制效果下降明显，均方差比值达到0.96以上，部分时刻甚至出现放大平台位移的现象。与TMD系统相比，NES虽然在TMD的共振频率附近振动控制效果弱于TMD，但NES系统的振动控制性能对刚度变化的敏感程度较小，NES系统对结构刚度的变化的鲁棒性更强。

图7 平台结构刚度变化对位移均方差比值的影响

4.2 NES振动控制机理分析

在系统参数确定后，建立系统内部瞬时能量传递的数学模型，通过系统内部瞬时能量传递的情况，来分析NES的瞬态响应和靶能量传递现象。首先根据系统动力学方程确定系统中的瞬时能量表达式：

NES中的瞬时能量

(9)

平台中的瞬时能量

(10)

NES内部瞬时能量占比

(11)

通过内部瞬时能量传递的数学模型，对随机波浪载荷作用下的平台与NES之间的瞬时能量进行分析，图8(a)、(b)给出了平台结构刚度为100%时NES系统和TMD系统中的瞬时能量传递情况。可以看出，在TMD系统中，TMD内部瞬时能量占比在100%～1%之间持续振荡，此现象说明系统中的能量在平台与TMD之间的传递是一个可逆的过程，并且这个可逆过程持续不断的发生，能量在平台与TMD交换的过程中，阻尼会消耗较多能量。而从NES系统曲线中可以得到，NES内部瞬时能量占比始终保持在90%以上并且曲线振荡的幅度和频率较小，说明在外载荷激励下，平台中的能量传递到NES后，除阻尼耗散外大多数能量储存在NES中，系统发生了靶能量传递，能量传递到NES中后几乎不会再发生逆向传递到平台。

分析图9(a)、(b)平台结构刚度下降为原刚度的45%时NES系统和TMD系统中的瞬时能量传递情况可知，TMD系统中，TMD内部瞬时能量占比依然在100%～1%之间保持较大的振荡频率，而NES系统中虽然瞬时能量占比的振荡幅值在某几个时刻有较大的增加，但总体上振荡的幅度保持在80%以上，而且曲线振荡的频率也明显小于TMD系统。这说明NES系统中能量逆向传递的发生频率依然小于TMD系统，NES系统中平台与NES之间依然存在靶能量传递。

((a)NES内部瞬时能量占比;(b) TMD内部瞬时能量占比。(a) Instantaneous energy ratio within NES; (b) Instantaneous energy ratio within TMD.)

((a)NES内部瞬时能量占比;(b) TMD内部瞬时能量占比。(a) Instantaneous energy ratio within NES; (b) Instantaneous energy ratio within TMD.)

为进一步分析NES产生靶能量传递的内在原因，利用小波变换对NES和TMD系统中平台和减振器的相对位移(x2-x1)进行时频特性分析。图10(a)、(b)给出NES和TMD系统平台结构刚度100%时系统小波变换时频谱，可以看出，平台刚度为100%时，TMD系统的相对位移响应能量大都集中在与平台固有频率0.326 Hz相同的频率，说明平台与TMD多数时间以相同的频率做同步运动。而NES系统的小波变化图像中可以看出系统响应量频率在0～0.5 Hz之间都有分布，这说明系统被激发出更多的频率分量，平台与NES振子在更宽频范围内出现瞬态共振俘获，使平台与NES之间产生靶能量传递。

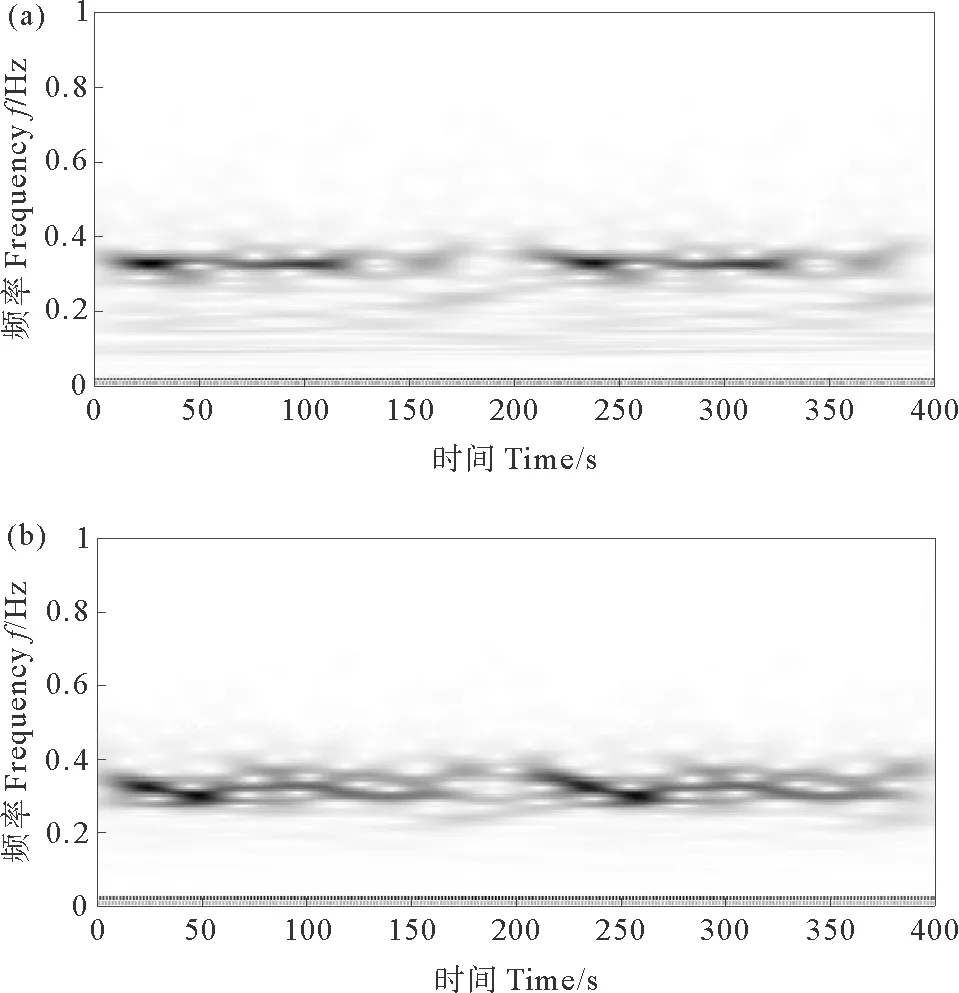
((a)NES系统；(b) TMD系统。(a)System of NES; (b)System of TMD.)

从图11(a)、(b)描绘的NES和TMD系统在平台结构刚度退化到原刚度45%时系统小波变换时频谱可以看出，由于刚度退化使平台本身固有频率变为0.219 Hz，TMD系统的相对位移响应能量依然集中在与平台固有频率0.219 Hz相同的频率，但响应能量相较于100%刚度时变小。而NES系统虽然相较于平台刚度100%时的频率分布变窄，但在某些时刻依然有高频分量存在，产生宽频范围内出现瞬态共振俘获。这也是刚度变化后NES系统振动控制效果优于TMD系统的原因。

((a)NES系统；(b) TMD系统。(a) System of NES; (b) System of TMD.)

5 结语

本文针对NES对受随机波浪载荷下导管架海洋平台第一模态的振动控制进行了参数优化和数值分析，比较了NES和TMD振动控制效果，计算表明：在平台的频率调谐区域内NES的振动控制效果比TMD的略差，但在其余远离共振区域内，NES的振动控制效果显著优于TMD，显示出NES可在更宽的频带范围内保持良好的振动控制性能，NES具有更好的刚度鲁棒性。基于系统内部瞬时能量传递的分析，得到NES系统中能够激发由平台到NES的靶能量传递，通过小波变换分析可知靶能量传递主要是由系统中的瞬态共振俘获激发的。