使用回折波走时数据的起伏地表速度建模方法*

何万利， 杨华臣， 张建中

(中国海洋大学海洋地球科学学院， 海底科学与探测技术教育部重点实验室， 山东 青岛 266100)

近地表低降速带速度和厚度的横向变化，会使来自其下部的地震波产生时移，导致地震资料成像畸变及解释错误。静校正是消除低降速带对地震成像影响的常规技术，其效果极大地依赖于近地表速度模型的精度[1-3]。在目前的地震资料处理中，主要用走时层析方法建立近地表速度模型[4]。走时层析通过反复迭代更新初始速度模型，使模型计算走时与实际观测走时的残差达到最小，从而建立近地表速度模型[5-8]。但这种方法的结果严重依赖于初始速度模型，且需要进行射线追踪运算，计算效率低。而基于速度随深度增加假设的回折波走时反演方法不需要初始速度模型和射线追踪，因而具有较高的效率，得到了广泛的研究和应用[9-12]。

Slotnick给出了基于水平地表假设且速度随深度线性增加的单层介质中的回折波方程[13]。Gibson进一步推导了多层介质回折波方程，利用“剥层”的思想提出了基于回折波方程的非线性最小平方反演[14]，该方法基于一维连续介质假设，计算横向均匀水平层状介质回折点速度信息。Osypov提出一种基于水平地表一维连续介质假设的无射线追踪层析静校正方法，该方法结合折射波和回折波，首先利用偏移距方程和走时方程直接估计视速度，再利用Herglotz-Wiechert公式计算视速度对应的深度，从而可得到近地表速度模型[15]。胡自多等采用时深曲线拟合和时距曲线拟合相结合的方法，消除地形起伏对初至走时的影响，再利用水平地表的回折波走时方程建立近地表速度模型，但这种方法不适用于速度横向复杂变化的情形[16]。Shi和Zhang等提出的剥层法，先对走时数据进行地形校正，再利用基于水平地表假设的回折波方程逐层建立近地表速度模型。在地形不复杂的地区，该方法可以取得与走时层析方法相当的建模效果，具有极高的效率[17]。但在地形复杂变化地区，通过地形校正难以消除地形起伏的影响，从而降低了速度建模的质量。

现有基于回折波走时的速度建模方法都是直接利用初至走时曲线计算射线参数，受地形起伏和初至走时误差的影响很大，而且基于水平地表假设的回折波走时方程不适用于近地表条件复杂地区。因此，本文建立了考虑地形起伏且速度横向变化的回折波走时方程。基于该方程，由各个炮检对的走时和偏移距数据反演射线参数，从而提出一种基于起伏地表回折波走时反演的速度建模方法，并用理论模拟数据和实测资料对本方法进行了测试，取得良好效果。

1 方法原理

由于压实作用，近地表地层速度通常随深度逐渐增加。在地表水平且速度随深度线性递增的连续介质中，地表观测到的初至波为回折波，其射线方程和走时方程可分别表示如下[14]：

(1)

(2)

其中：x0表示偏移距；t0表示初至走时；v0表示地表速度；p表示回折波射线参数；b表示速度梯度。

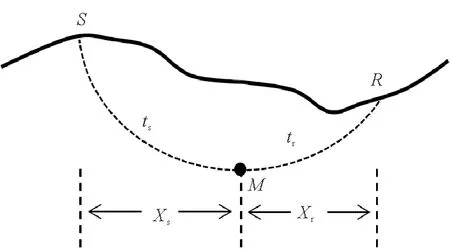
(S表示炮点，R表示检波点，M表示回折点。实线表示观测面，虚线表示回折波射线路径。S denotes a source, R denotes a receiver and M denotes a turning-point. The solid line denotes the observation surface, and the dotted line denotes the ray path of diving-wave.)

然而，实际地形往往起伏，且地层速度存在横向变化。因此，假设炮点端速度为vs,0，检波点端速度为vr,0，速度梯度为b，射线路径如图1所示。这时，回折波从炮点传播至回折点的射线方程和走时方程可表示为：

(3)

(4)

其中：Xs为炮点至回折点的水平距离；ts为炮点至回折点的走时；vs,0为炮点处地表速度；p为射线参数；b为速度梯度。同理，回折波从回折点传播至检波点的射线方程和走时方程可以表示为：

(5)

(6)

其中：Xr为回折点至检波点的水平距离；tr为回折点至检波点的走时；vr,0为检波点处地表速度。炮检点间的回折波水平距离，即偏移距X和走时t应满足：

X=Xs+Xr。

(7)

t=ts+tr。

(8)

联合式(3)～(8)，可得图1所示的回折波射线方程和走时方程，分别表示为：

(9)

(10)

方程(9)和(10)区别于方程(1)和(2)之处在于方程(1)和(2)基于水平地表假设，故其只包含一个地表速度，而方程(9)和(10)考虑到地形起伏，用两个地表速度表示回折波的传播规律，分别为炮点处地表速度和检波点处地表速度。由式(9)和式(10)消去速度梯度b，可得：

(11)

式(11)是一个非线性方程，其中偏移距X可从观测系统信息中得到，初至走时t可通过拾取得到，vs,0和vr,0可由近道直达波估算得到或通过其它资料得到，故只有变量p是未知的，且同时具有约束条件1/p>vs,0和1/p>vr,0。由此，可用二分法求解方程(11)得到射线参数p。在求得射线参数p后，回折点速度vm为：

(12)

将射线参数带入式(9)，可求得速度梯度b为：

(13)

回折点M的空间坐标(xm,ym,zm)为：

xm=xs+Xscosθ，

(14)

ym=ys+Xssinθ，

(15)

(16)

其中：(xs,ys)表示炮点坐标；Xs为炮点至回折点的水平距离；θ表示炮检点连线的方位角；zm,0表示回折点在炮检点所在观测面投影点的深度(当观测面位于地表时，zm,0=0)；vm,0表示回折点在炮检点所在观测面投影点的速度。

在实际处理时，考虑到偏移距非均匀分布，将每一个共中心点道集按照偏移距大小进行选排并分段。如图2所示的按偏移距段计算回折点位置示意图，炮检对Sk,1Rk,1，Sk,2Rk,2，…，Sk,MRk,M处于第k个偏移距段，而炮检对Sk+1,1Rk+1,1，Sk+1,2Rk+1,2，…，Sk+1,N，Rk+1,N处于第k+1个偏移距段。假设同一个偏移距段对应的走时资料反映地下同一层介质的信息，则可以用第k个偏移距段对应的走时资料计算其对应的回折点Ck的位置及速度信息，同理可用第k+1个偏移距段对应的走时资料计算其对应的回折点Ck+1的位置及速度信息。

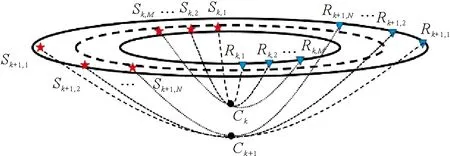
(红色五角星表示炮点，蓝色三角形表示检波点，Ck和Ck+1分别为第k个偏移距段和第k+1个偏移距段对应的回折点。Sk,1Rk,1，Sk,2Rk,2，…，Sk,MRk,M和Sk+1,1Rk+1,1，Sk+1,2Rk+1,2，…，Sk+1,NRk+1,N分别表示第k个偏移距段和第k+1个偏移距段对应的射线路径。The red pentagrams represent the sources, the blue triangles represent the receivers, and Ck and Ck+1 represents the turning-point. The dashed and dotted lines represent ray paths.)

当所有炮检点在同一水平面上，且地下介质横向均匀时，共偏移距段的所有炮检对的回折点位置相同，但实际上由于地形起伏以及速度横向变化的影响，共偏移距段计算出的回折点位置不完全相同，应该聚集在一个小区域内。假设该区域成空间球状，利用最小二乘拟合算法估计这些离散回折点的统计平均位置，即求解球心位置坐标(xc,yc,zc)和球的半径R，使下列目标函数达到最小：

(17)

其中：J表示离散回折点个数；(xj,yj,zj)表示第j个离散回折点的坐标。求出平均回折点空间坐标后，再利用加权平均方法估计回折点位置的速度：

(18)

其中：vc表示回折点的速度；vj表示半径为R的球内第j个离散回折点的速度；wj表示第j个离散回折点速度的权系数。距离球心近的速度值应给予较大的权重，而距离球心远的速度值应给予较小的权重，从而采用反距离加权，权系数为：

(19)

其中：dj表示第j个回折点到球心的距离；α为一个任意正实数，通常取α=2。

求得回折点位置及其速度后，该地层的垂直速度梯度为：

(20)

其中：bc表示速度梯度；vc,0和zc,0分别表示回折点在炮检点所在观测面的投影点处的速度和深度。对于第一层介质，vc,0表示回折点在地表的投影点处的速度，且zc,0=0。

选取某个共中心点道集，先用第一个偏移距段的走时资料，按上述方法计算第一层介质的速度信息，然后，把第一层介质的效应从第二个偏移距段的走时资料中剥离掉，再用剩余的第二个偏移距段的走时资料，按上述方法计算第二层介质的速度信息。传至第二层介质的回折波在第一层介质传播的水平距离和走时分别为：

(21)

(22)

则剥离第一层介质后，在第二层介质传播的回折波偏移距Xr和走时tr为[17]：

Xr=X-ΔX,

(23)

tr=t-Δt。

(24)

如图3所示，在一个共中心点道集内，从小偏移距到大偏移距，按顺序重复上述步骤，就可得到该共中心点处从地表到深部的地层速度分布。对所有共中心点道集数据进行同样的处理，就可获得整个工区的三维速度模型。

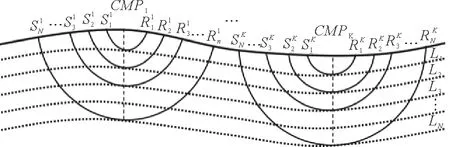
(CMP1和CMPK分别表示两个共中心点道集。分别表示CMP1共中心点道集对应的射线路径，分别表示CMPK共中心点道集对应的射线路径。CMP1 and CMPK represent two common midpoint gathers respectively. S and R denote sources and receivers, respectively. Thin solid lines denote ray paths and dotted lines denote the interfaces connecting turning-points.)

2 模型测试

为了测试本文方法的正确性，建立了一个地形起伏以及速度横向变化的速度模型，如图4(a)所示，图4(b)为该模型在y=0.5 km处的切片。模型大小为2×1×0.5 km3，地表最大高程差为160 m，最小速度约为1 500 m/s，最大速度约为4 000 m/s，纵向速度随深度增加。布设10条炮线，20条检波点线。每条炮线40个炮点，炮间距为50 m，炮线距为100 m。每条检波点线79个检波点，检波点间距为25 m，检波点线距为50 m。采用5×5×4 m3的规则网格离散模型，利用LTPI射线追踪方法[18]获取初至走时数据，然后分别用基于初至走时曲线拟合求取射线参数的常规方法和本文方法建立了速度模型。

图4(c)和(d)分别为常规方法反演模型及其在y=0.5 km处沿x方向的切片，图4(e)和(f)分别为本文方法反演模型及其在y=0.5 km处沿x方向的切片。为进一步说明本文所述速度建模方法的效果，我们分别计算了常规方法反演模型和本文方法反演模型的相对误差，并截取相对应的速度误差切片进行比较分析，图5(a)和(b)分别是常规方法反演模型和本文方法反演模型的相对误差在y=0.5 km处沿x方向的切片。可以看出常规方法反演模型相对误差整体偏大，这是由于常规方法通过初至走时曲线拟合求取射线参数，受地形起伏的影响，射线参数求取不准，使得速度误差相对较大。本文方法基于考虑地形起伏和速度横向变化的回折波方程，反演获得较为准确的射线参数，因而速度误差相对较小。

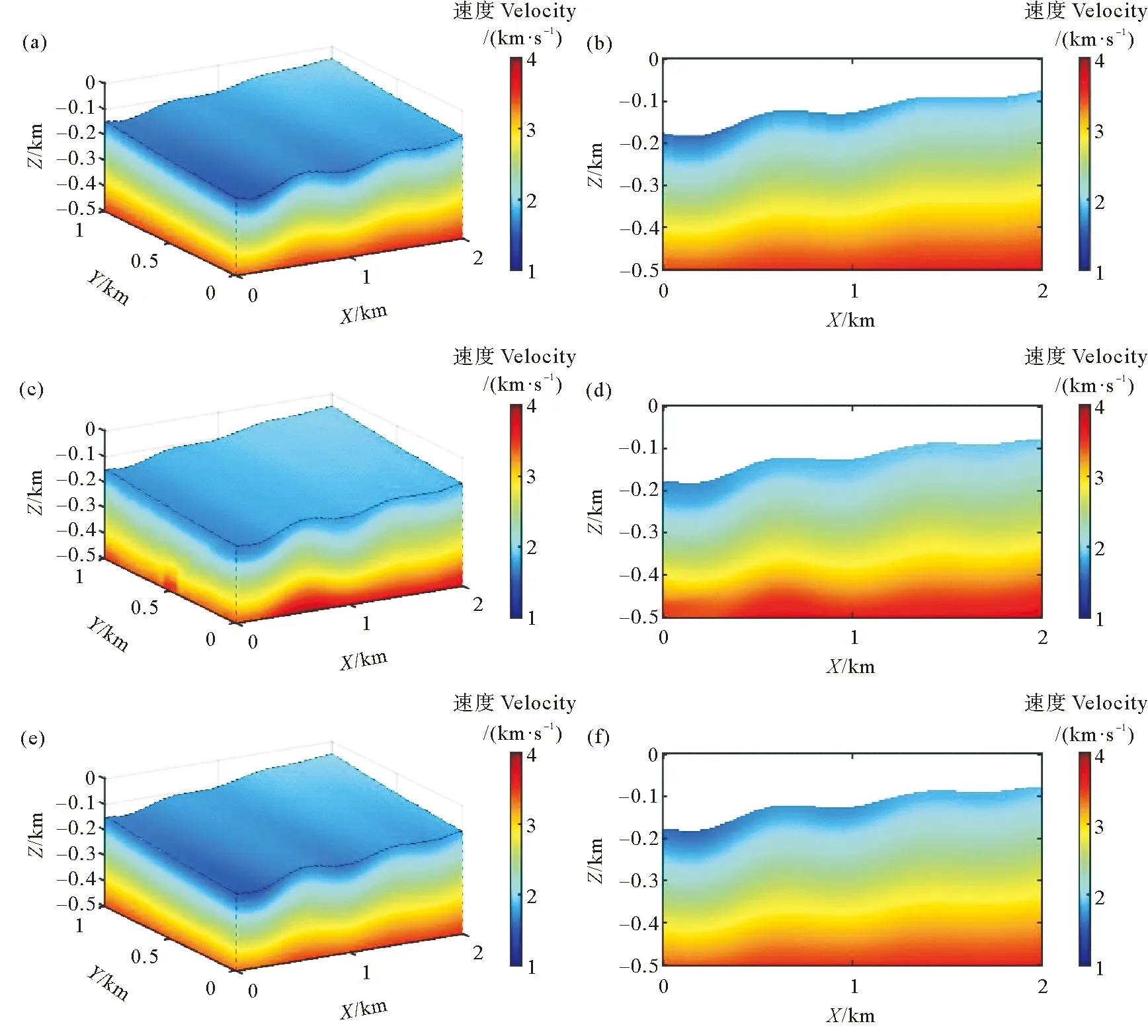
((a)理论速度模型；(b)理论速度模型在y=0.5 km处的切片；(c)常规方法反演模型；(d)常规方法反演模型在y=0.5 km处的切片；(e)本文方法反演模型；(f)本文方法反演模型在y=0.5 km处的切片。 (a) and (b) the theoretical velocity model and its slice at y=0.5 km, respectively; (c) and (d) the model inverted by the layer-stripping method and its slice at y=0.5 km, respectively; (e) and (f) the model inverted by the method proposed in this article and its slice at y=0.5 km, respectively.)

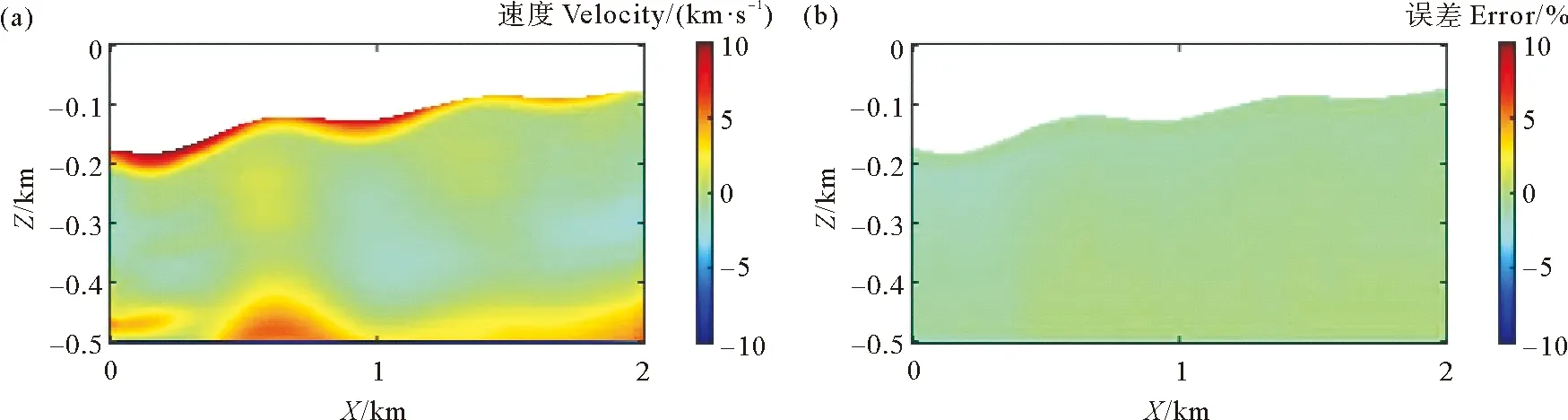
((a)常规方法反演模型相对误差；(b)本文方法反演模型相对误差。 (a) The relative error of the velocity model inverted by the layer-stripping method; (b) The relative error of the velocity model inverted by the method proposed in this article. )

3 实际资料应用

为了检验本文方法在近地表条件复杂地区的实际应用效果，将本文方法应用于青海某山前带三维实际地震资料。该工区的地形如图6所示，整个工区长20 km，宽2 km,工区内最小高程1 633 m，最大高程1 914 m，工区地形起伏较大，近地表条件复杂。图7为该工区的观测系统，共有524个炮点，3 054个检波点，炮点不等间距布设，检波点道间距为50 m。地震记录采样间隔为4 ms，记录长度为6 s。

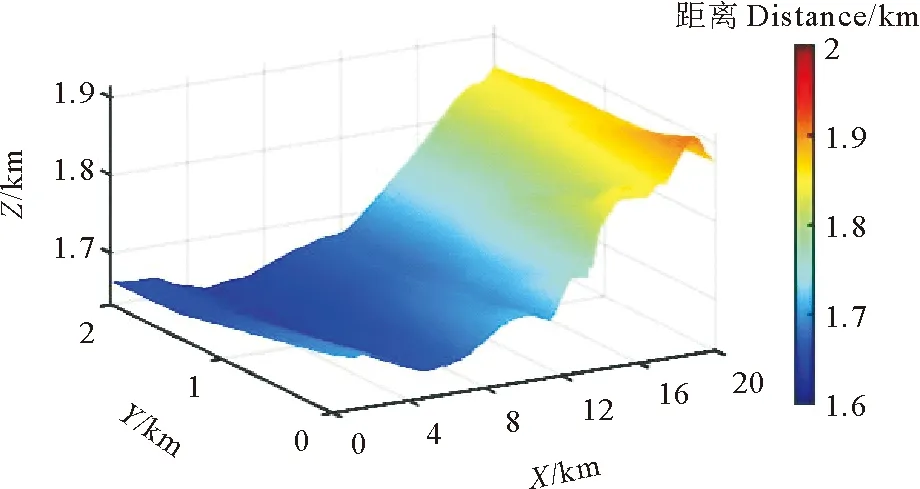
图6 工区地形图

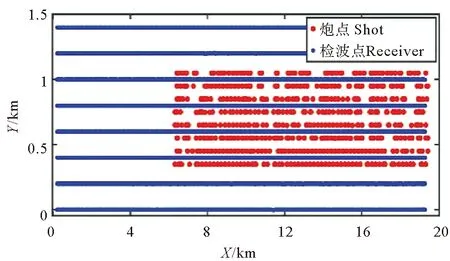
(红点代表炮点，蓝点代表检波点。Red points denote sources and blue points denote receivers.)

从原始地震记录中拾取初至走时，并分别利用常规方法和本文方法建立近地表速度模型，如图8所示，图8(a)、(b)分别是常规方法反演模型以及在y=0.5 km处沿x方向的切片，图8(c)、(d)分别是本文方法反演模型以及在y=0.5 km处沿x方向的切片。取基准面高程2 000 m，替换速度2 500 m/s，分别利用常规方法和本文方法建立的近地表速度模型，对原始地震数据进行静校正处理，第10条CMP线的叠加剖面如图9所示。图9(a)是利用常规方法模型进行静校正处理后的叠加剖面，其同相轴存在扭曲、不连续等现象，图9(b)是利用本文方法模型进行静校正处理后的叠加剖面，在图9(a)中扭曲、不连续的同相轴，变得更加连续、清晰，叠加效果改善明显，说明了本文方法在复杂近地表条件的良好应用效果。

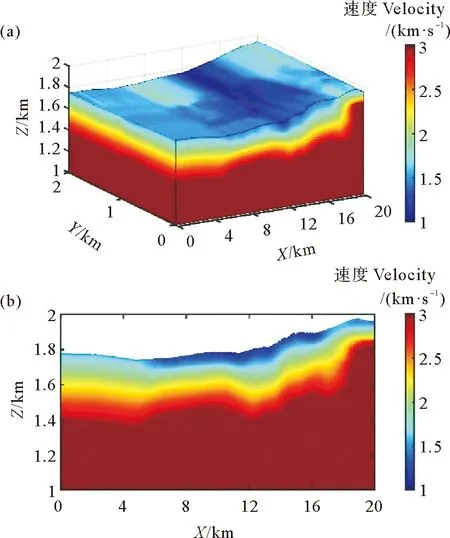
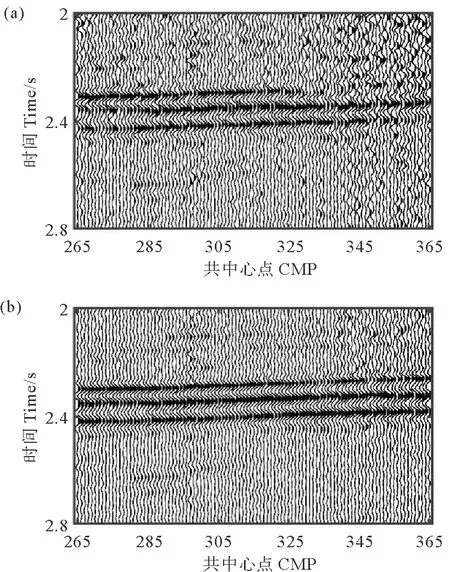
((a)利用常规方法反演模型计算静校正量，(b)利用本文方法反演模型计算静校正量。 (a) Statics obtained by layer-stripping method; (b) Statics obtained by the method proposed in this article.)

4 结语

本文考虑地形起伏和地层速度横向变化，提出将共中心点道集按偏移距大小进行选排并分段从而确定回折波的回折点位置和速度的方法。其中，射线参数的求取不同于常规方法那样直接由走时曲线得到，而是利用炮检对的走时和偏移距数据反演得到，从而避免了地形起伏和走时数据误差的影响。把每个共中心点道集按照偏移距段进行选排，按偏移距从小到大的顺序，分别计算出从浅部到深部的回折点位置和速度，获得整个工区的三维速度分布，从而形成了利用回折波走时数据的起伏地表速度建模方法。相比常规回折波反演方法，对起伏地形和地层横向速度变化等复杂情况具有更强的适应性和更高的建模精度。

在近地表层复杂变化地区，本文方法不如基于射线追踪的走时层析反演方法的精度高和适应性强，但具有效率高的优势，可以为走时层析反演或波形反演提供较好的初始速度模型。与常规回折波反演方法一样，本文方法也基于速度随深度递增的假设，故而当地下介质满足这种假设时，本文方法能够取得较好的效果，而当近地表地层不满足这种假设，如地层存在速度反转时，该方法将会存在一定的局限性，这是进一步需要研究的问题。

致谢：感谢王金龙在理论模型初至走时计算方面提供的帮助。