云南省滑坡灾害分形特征研究与分形评价模型探讨

史兴旺，管新邦，边 筠

(煤炭科学技术研究院有限公司安全分院，北京 100013)

分形理论在分析复杂的非线性系统方面取得了良好的效果[1]。例如Sivakumar B.[2]论证了运用多重分形理论框架解释不同气候带降雨特征的可行性，Kotowski P.[3]提出了一套完整的方法来测量铁基合金表面断裂的分形维数，并证明所测断裂面的分形维数不依赖于该研究对象的材料，Zhang Y等[4]将分形理论运用到城市地理中，来反映和模拟城市边界形态。对于滑坡灾害来说，因其受到多种因素的综合作用和影响，滑坡地表变形演化过程往往具有复杂的非线性特征[5]，并且随着荷载值增大整体呈现非线性增大的趋势[6]。这为适用于解决复杂非线性问题的分形理论找到了合适的切入点。近年来，分形理论在滑坡研究领域也受到了部分学者的关注和认可。例如Katz O.等[7]通过模型实验探讨了边坡破坏类型和破坏频率之间的分形关系，Li C等[8]分析了滑坡发生和降雨之间的幂指数关系。此外，针对滑坡位移趋势研究，郑明新等[9]分析了滑坡演化过程中滑坡变形曲线的分维特征，并首次提出了滑坡大滑分维预报公式。樊晓一等[10]对不同稳定状态下地震滑坡的地形剖面线的多重分形维数演化特征进行了研究，并表明相对稳定滑坡的多重分形维数演化特征具有明显的有序性。

综合前人研究，本文以分形理论为基础，对研究区滑坡的分形特征进行研究，获得不为整数的分形维数，进一步得到基于分维数的滑坡灾害对不同影响因素的相关性，与逻辑回归模型、证据权模型、证据可信度函数模型和信息量模型所得到的相关性具有较高的一致性。滑坡的几何形态及空间分布具有复杂的不确定性，不同的滑坡类型有不同的形态特征，几何形态特征和空间分布对于滑坡的研究有着重要的意义，分形理论可对建立滑坡灾害易发性评价模型提供新的科学模型。

1 研究方法

世界是非线性的，自然界中分形无处不在。分形理论是用分数维度的视角和数学方法描述和研究客观事物，该理论认为局部特征形态与整体特征形态具有自相似的特征。分形理论突破了从传统的点线面和时空的研究方法，是一门以不规则几何形态为研究对象的新几何学。分形理论已经应用到图像处理、自然科学、管理学、工程技术、经济学和文化艺术等各个方面。分维是分形理论中的基本参数和重要原则。研究滑坡的分维值可以了解其复杂程度和演化规律。滑坡活动强度的升高将呈现出其分维值的升高，分维值较高时，则面临较高的产生滑坡的可能性。滑坡产生后其分维值降低，可以根据某个时期内斜坡系统分维值的变化及其升幅的大小来预测滑坡产生的数量[11]。

本文采用遥感数据为高分一号遥感数据，解译识别的滑坡灾害数据库分析。通过对遥感图像进行正射校正、图像融合、图像增强处理和图像镶嵌与裁剪以及配合大量的野外调查，特别是小比例尺的地质灾害详查完成解译。结合云南省图件资料的整理和对云南省滑坡编录资料的分析，利用盒维数法对研究区的滑坡灾害分形特征进行分析研究。

(1)常维分形可用公式表示为：

N=Cr-D.

(1)

其中，N为特征尺度为r的物体数目，r为特征尺度，C为常数，D为分维数。

其定义为：设A属于RN，在欧氏距离下，统计用边长1/2n的盒子个数Nn(A)，则有：

(2)

当n增大时，统计计算Nn(A)，随着一组系列的r1，r2，……rn，得到一组N(r1)，N(r2)，……N(rn)，以点[log(r)，logN(r)]为坐标作双对数图，利用最小二乘法，拟合成一条直线得出斜率，其绝对值即为分形维数。其直线公式为：

lnNn(A)=a+b1/ln2n.

(3)

其中a为常数，b为分形维数。

(2)变维分形其函数关系表示为：

D=g(r).

(4)

对于N与r之间的函数关系N=f(r)，令f(r)=Cr-D，则有

(5)

有研究表明，任一参数A随重现期的变化规律均可以转化为变维分形的形式。若将常维分形看作1阶分形，若其中的常维分形为D=C′/rD′，则可以对1阶分形再进行一次分形，以此类推可得到N阶分形[12]。其表达式为：

N1=C1/rD1.

(6)

其中D1=C2/rD2；D2为常数。

N2=C1/rD1.

(7)

……

N阶分形，其中Dn-1=Cn/rDn；Dn为常数。

Nn=Cn-1/rDn-1.

(8)

由此可见，对于任意阶的变维分形，都可以转化为常维分形的形式。多阶分形可以通过阶数累计处理，衍生出累计和变化分形。具体步骤为：

1)将原始数对(Ni，ri)按照从小到大的序列投影到双对数坐标系中，计算相邻两点间在双对数坐标系中的Di,i+1。Di,i+1的求解公式为：

Di,i+1=ln(Ni/Ni+1)ln(ri/ri+1).

(9)

2)对(N1,N2,L,Ni,L,Nn)进行累计和计算。

{S1i}={N1,N1+N2,N1+N2+N3,…};i=1,2,3,…,n.

(10)

{S2i}={S11,S11+S12,S11+S12+S13,…};ji=1,2,3,…,n.

(11)

{S3i}={S21,S21+S22,S21+S22+S23,…};i=1,2,3,…,n.

(12)

{Sni}={S(n-1)1,S(n-1)1+S(n-1)2,S(n-1)1+S(n-1)2+S(n-1)3,…};i=1,2,3,…,n.

(13)

其中，S1，S2，S3，…Sn为相应分形阶数的累计和序列。

3)根据以上公式，由S1i可以得到在双对数坐标系中的n-1条斜率不等的线段，这些斜率的相反数则为一阶累计和变维分形维数，同理可以得到高于一阶累计和变维分形维数。随着分形阶数的增加，双对数坐标系中的各阶累计和形成的数据点最终会呈现出很好的线性关系。此时可以用线性回归模型计算该线性关系的参数，得到其常分维数D。

2 常维分形特征

常维分形是指分维数D不随特征尺度r的变化而变化，二者之间不存在某种函数关系。在不考虑滑坡地质灾害分布地区的地貌地形特征，把滑坡看作是二维平面上的点，运用盒维数法来研究常维分形。盒维数法是一个常用而又简单的方法，在操作过程中利用公式不断缩小盒子的尺寸，建立尺寸为2n的灰度图像，与灾害点图像覆盖，得到各尺寸盒子与点的相交程度，然后在对数坐标系中建立相交盒子个数N与盒子尺寸r的散点图，采用最小二乘法进行线性拟合，验证其拟合程度的相关系数，所得拟合直线的斜率即为待求图形的分形维数。

在滑坡地质灾害的空间分布关系中，同样可以用盒维数法进行分形特征的研究。图1为滑坡空间地质灾害的双对数模型，线性回归方程为：y=-0.8432x+6.8836，R2=0.9906。其拟合程度接近于1，说明云南省的滑坡地质灾害在空间分布上具有明显的分形特征。可以看出研究区的滑坡分布受制于一定的分形维数，又因为滑坡产生后其分维值会降低，我们可以求解不同时期的研究区的滑坡分维值，统计其变化趋势特征，预测研究区滑坡是否会发生，同时可以根据分维降低的幅度，预测滑坡数量和规模。

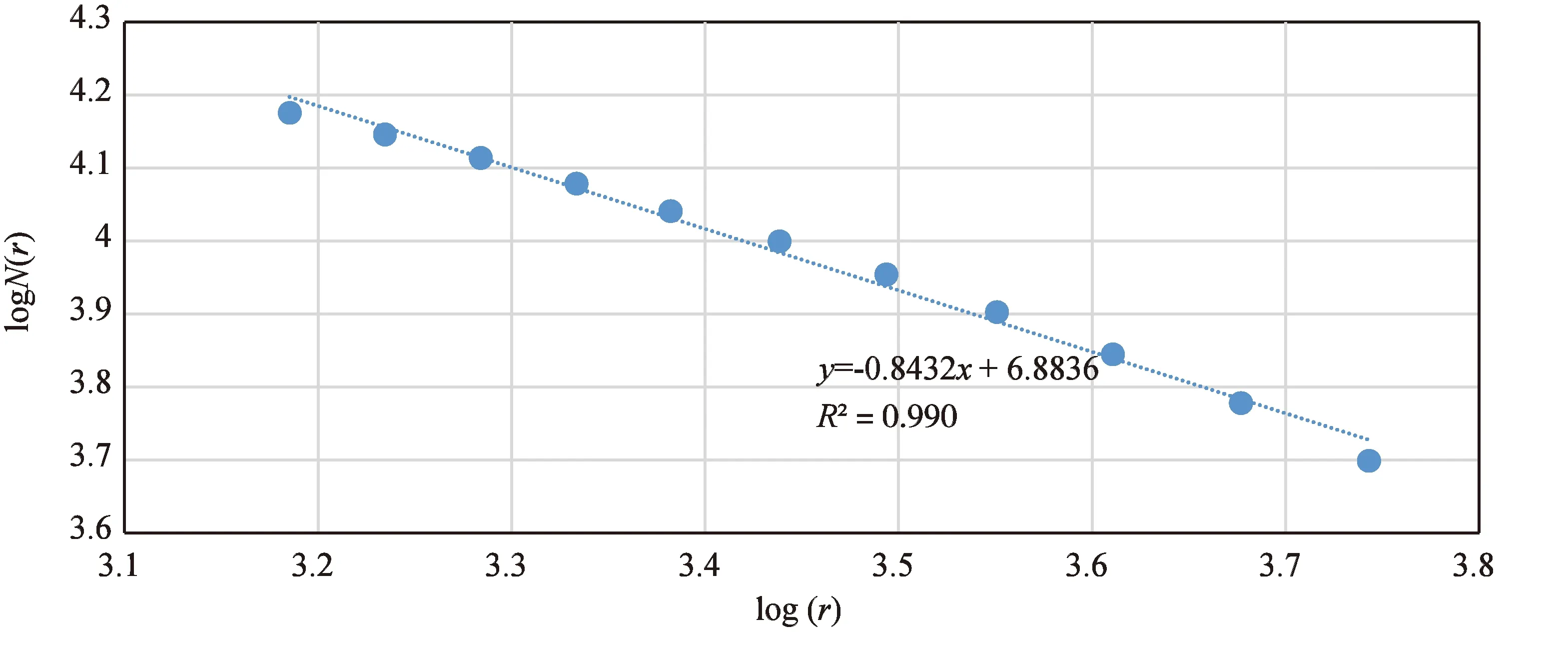
图1 云南省滑坡点空间分形特征Fig.1 Yunnan landslide spatial fractal features

云南省的水分、地形与构造等条件的组合对滑坡灾害的频繁发生提供了便利，从而表现出滑坡空间维数值D=0.8432，高于中国大陆及三大分区滑坡空间分维值[13]，说明云南省滑坡灾害在全国范围来讲属于高发区。

基于“过去和现在是打开将来之门的钥匙”理论，过去和现在的滑坡的空间分布，将来也将是最有可能发生滑坡的地区[14]。因此，在进行滑坡易发区评价时，可以运用滑坡的分形公式进行拟合，计算滑坡周围不同距离内发生滑坡的概率。因此，在进行滑坡相关分析中，应研究不同区域的分形特征，对比不同地区滑坡灾害的分维值，建立分维值分区，对分维值大的因素要重点考虑。

3 滑坡影响因子与空间分布变维分形特征

研究滑坡的分布与其影响因子的分形关系，可以得到滑坡对不同影响因素的相关性，进而为易发性的评价和分区提供基础资料。然而在这类相关研究中，严格满足常维分形的事件是没有的，这时常维分形则常常不能满足工作需要。在分形中，分维数D不是常数，而是与特征尺度r之间存在着某种函数关系时，即为变维分形。

3.1 滑坡面积与坡度的分形特征

坡度是控制滑坡发育的重要因素之一。按照坡度步长为10°，对滑坡面积和与坡度区间进行统计，见表1所示。可以看出随着坡度的增加，图形出现先增后减的趋势，在20°到30°之间出现峰值。对数据进行双对数变换处理，发现并不呈现出常维分形的特征；对数据进行高阶累计和变换处理，可以看出滑坡面积的空间分布与坡度在4阶累积和曲线上呈现很好的线性关系，见图2。对4阶累计和变换数据进行线性回归拟合，R2=0.9968，拟合相关系数接近于1，这表明滑坡面积空间分布与坡度呈4阶累积和变维分形关系，其分维值D4=2.1384。

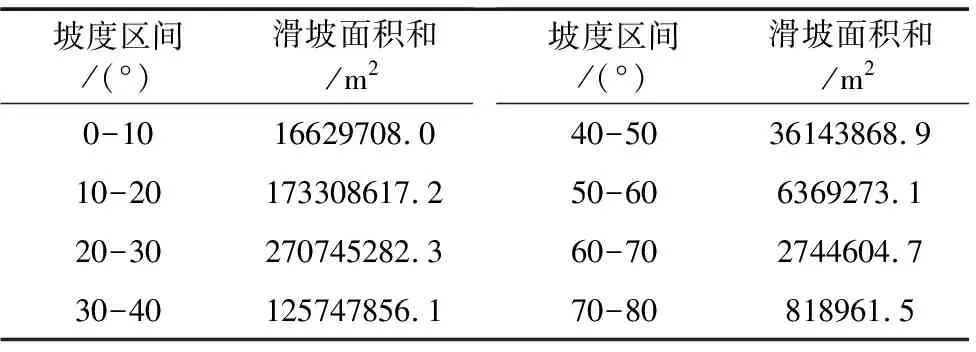
表1 坡度区间与滑坡面积关系统计表Table 1 Interval slope and landslide area relationship tables

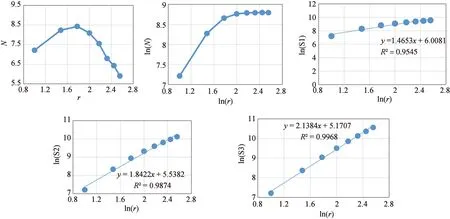
图2 滑坡面积与坡度分维数分形特征Fig.2 Landslide area and slope fractal dimension characteristic curve

3.2 滑坡面积与高程的分形特征

高程的增加会影响滑坡地质灾害的发生概率和规模大小。按照高程步长为500 m，对滑坡面积和与高程区间进行分等级统计，大于3 500 m为一个等级，见表2所示。可以看出，随着高程的增加滑坡面积与高程之间并不存在明显的线性关系。对滑坡面积与高程之间进行高阶累计和变维分形变换，在3阶累计和与特征尺度r的双对数模型中具有很好的线性关系，见图3。表明滑坡面积与高程之间存在着3阶累计和变维分形关系，其分维值D3=3.5059，相关系数R2=0.9961，拟合相关系数接近于1。

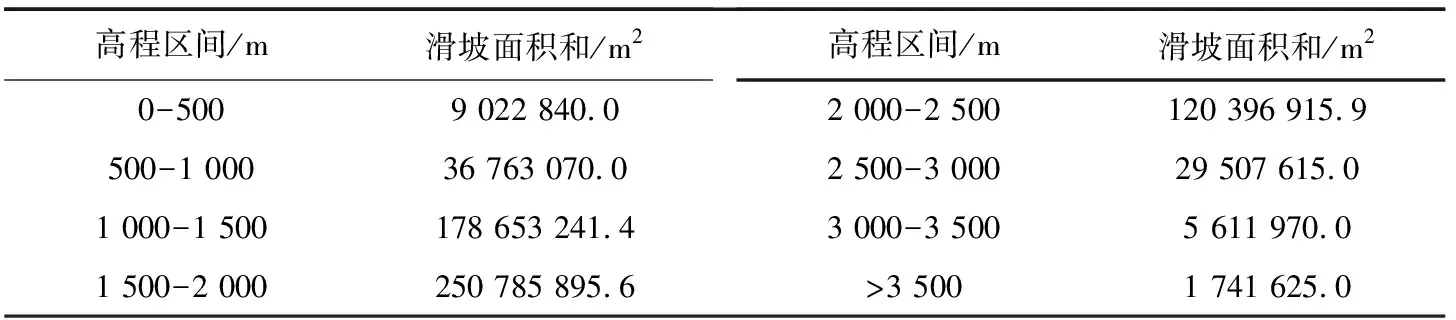
表2 高程区间与滑坡面积关系统计表Table 2 Elevation range and landslide area relationship tables

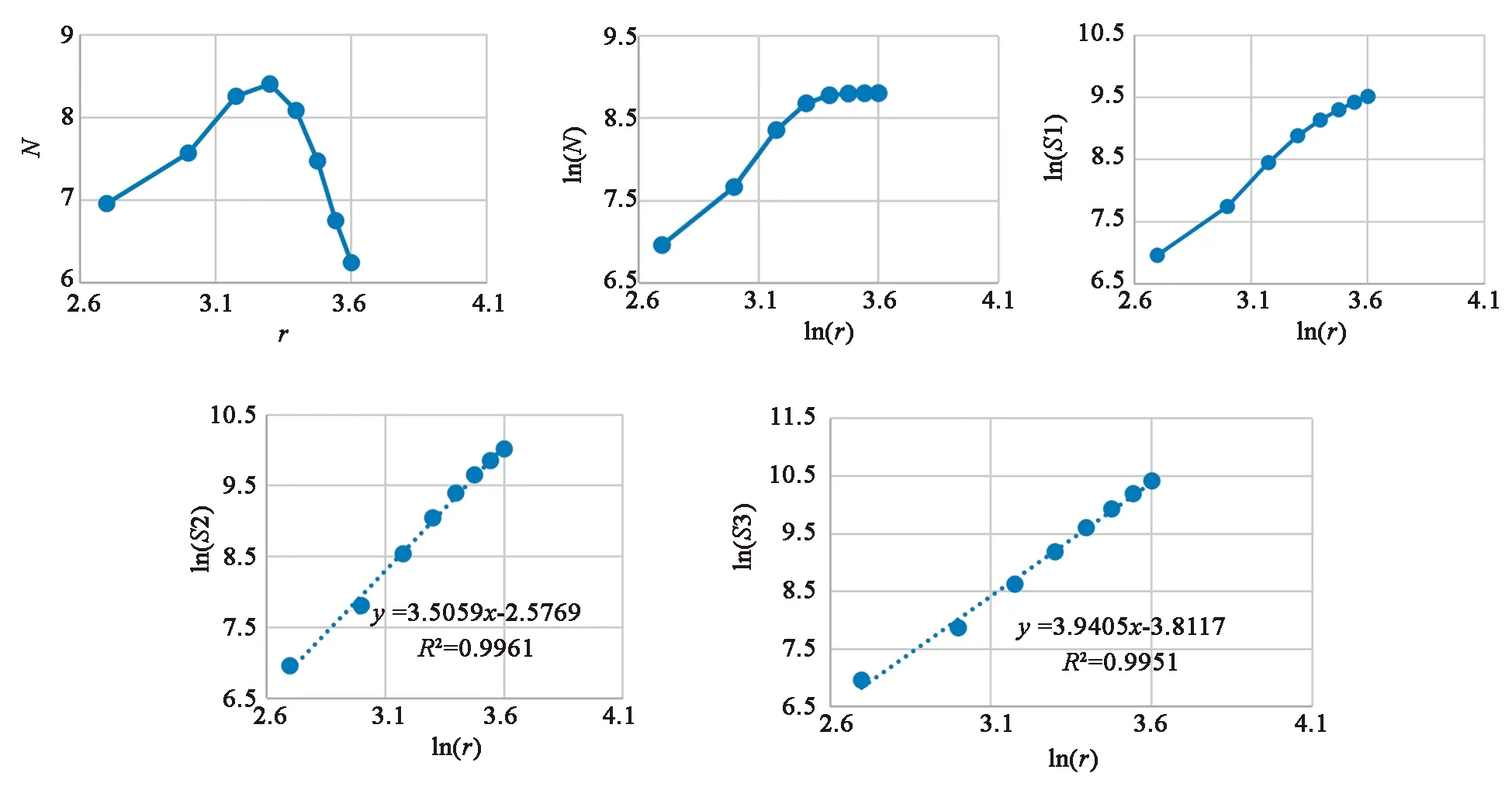
图3 滑坡面积与高程分维数分形特征Fig.3 Landslide area and elevation fractal dimension characteristic curve

3.3 滑坡面积与断裂缓冲区之间的分形特征

在ArcGIS中对断裂缓冲区设计步长为1 km、缓冲半径为10 km的缓冲区，统计各缓冲区内滑坡地质灾害的面积，见表3所示。可以看出在双对数关系中，滑坡面积与断裂缓冲区之间不存在常维分形特征。在高阶累计和变维分形变换中，滑坡面积与断裂缓冲区在2阶累计和双对数模型中的线性关系要好于3阶累计和模型的线性关系，见图4。其线性回归曲线拟合程度R2=0.9992，拟合相关系数接近于1。表明滑坡面积与断裂缓冲区存在2阶累计和变维分形关系，其分维值D2=1.6005。

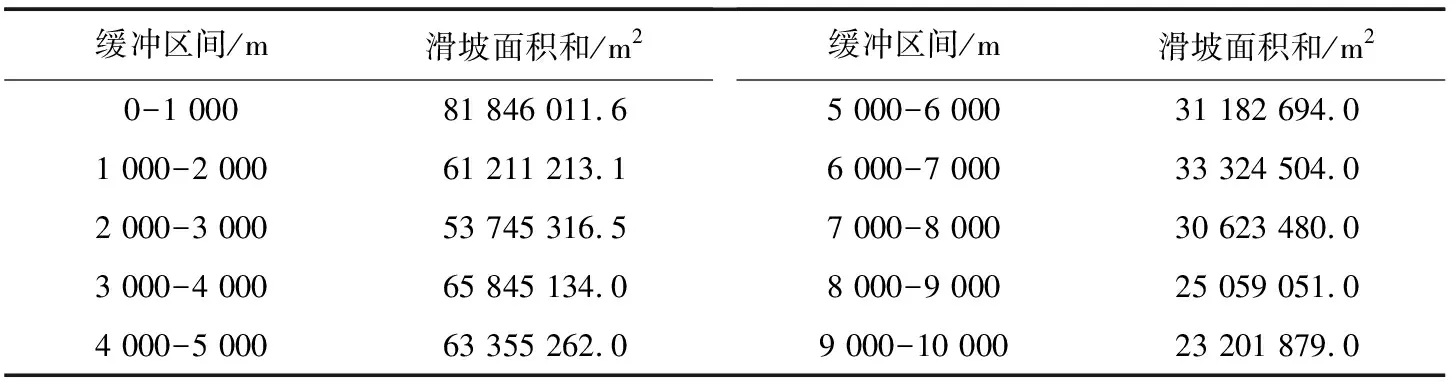
表3 断裂缓冲区间与滑坡面积关系统计表Table 3 Fracture buffer range and landslide area relationship tables

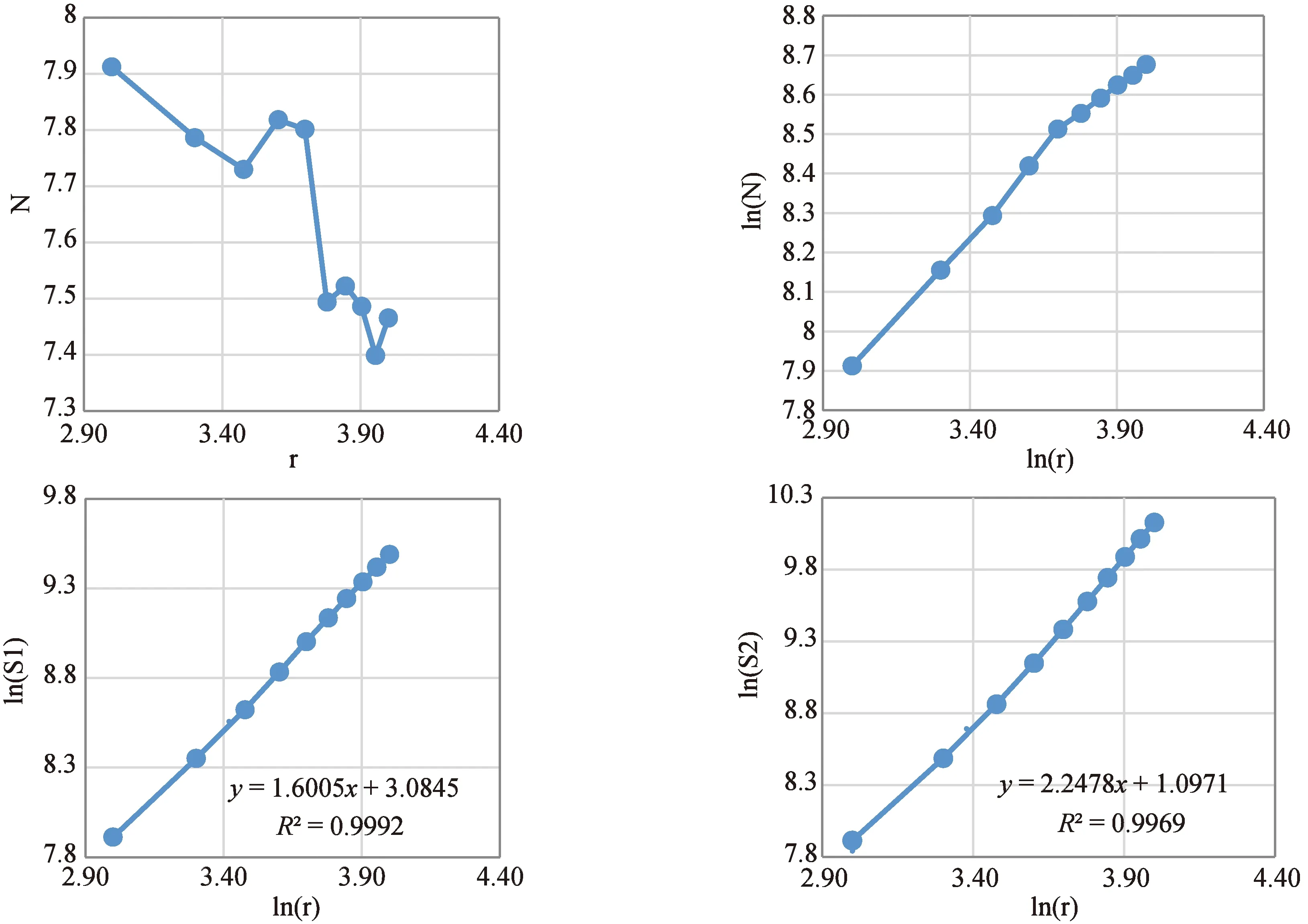
图4 滑坡面积与断裂缓冲区分维数分形特征Fig.4 Landslide area and fracture buffer range fractal dimension characteristic curve

3.4 滑坡面积与岩性之间的分形特征

根据岩性的软硬程度属性，运用数字代码建立滑坡面积与岩性之间的关系，见表4所示。可以看出在高阶累计和变维分形中，滑坡面积与岩性在2阶累计和双对数坐标系中存在着最优的线性关系，见图5，其拟合相关系数R2=0.9899，拟合相关系数接近于1。表明滑坡面积与岩性之间存着在2阶累计和变维分形，其分维数D2=2.3876。

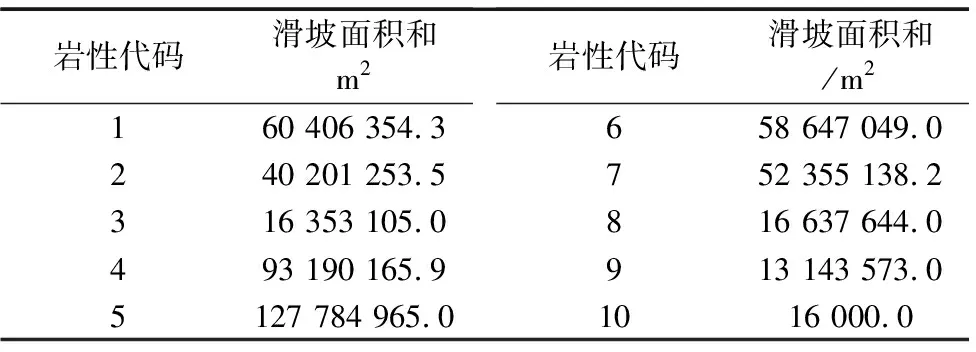
表4 岩性软硬等级与滑坡面积关系统计表Table 4 Lithology grade and landslide area relationship tables

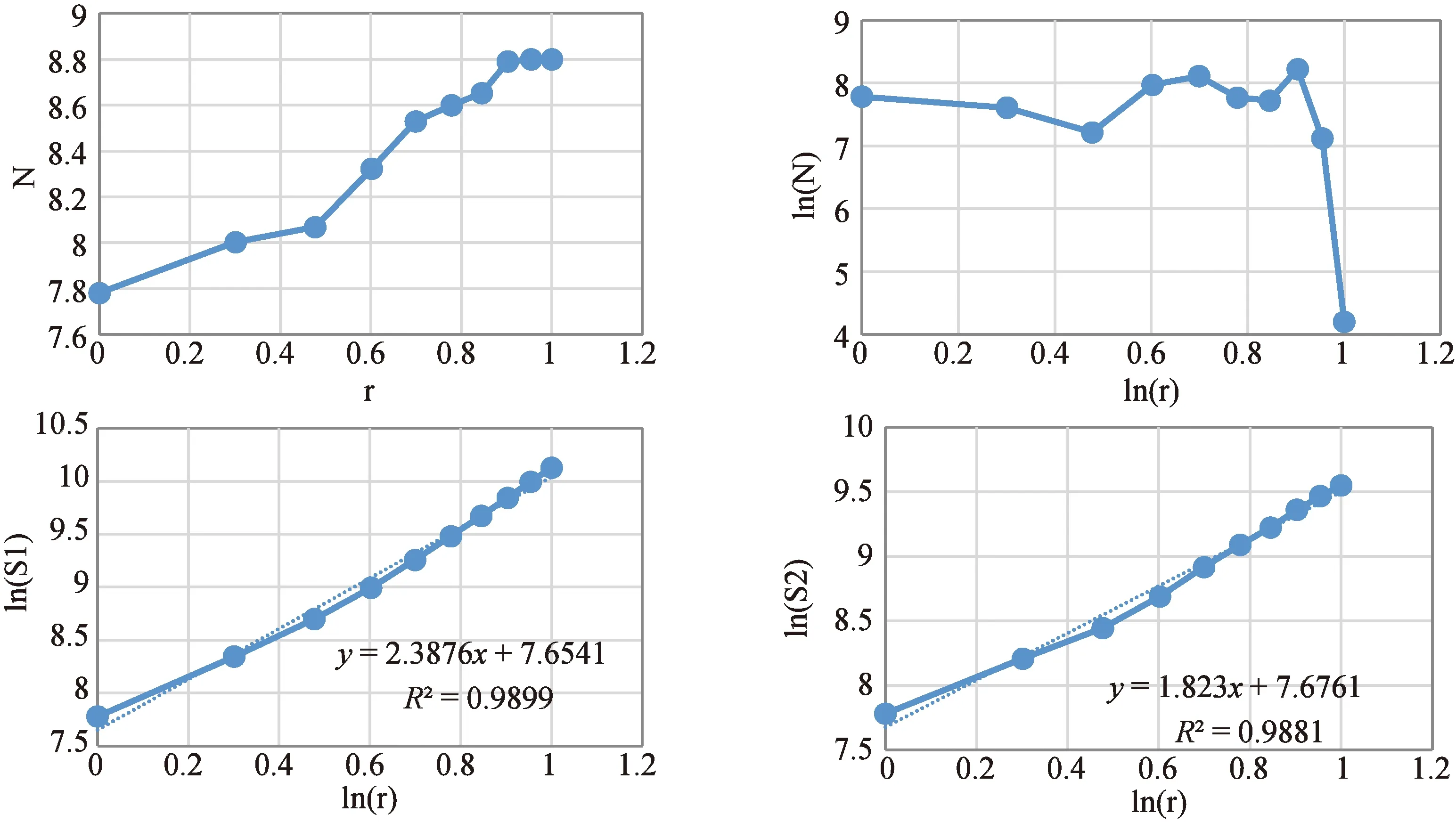
图5 滑坡面积与岩性分维数分形特征Fig.5 Landslide area and lithology grade fractal dimension characteristic curve

4 结果分析

以上研究结果表明，云南省滑坡地质灾害在空间上具有明显的分形特征。云南省滑坡地质灾害的面积空间分布与坡度、高程、断裂缓冲区和岩性等环境因子呈现不同阶的变维分形特征：与断裂缓冲区和岩性呈现2阶累计和变维分形，与高程呈现3阶累计和变维分形，与坡度呈4阶累计和变维分形。分维值分别为坡度D4=2.1384，高程D3=3.5059，断裂缓冲区D2=1.6005，岩性D2=2.3876。

为了研究滑坡灾害的分布与各环境因子之间的变维分形的关系，分别采用了逻辑回归模型[15-17]、证据权模型[18-19]、证据可信度函数模型[20-21]和信息量模型[22]对研究区的滑坡灾害与影响因素的关系进行了统计分析，分别得到了回归系数、C值、Bel值和信息量值。这些量值分别代表了这4种评价模型所构建的影响因素在滑坡灾害事故发生中的权重，其量值的大小即为影响因素权重值的大小。对比发现分形维数与以上四种方法得到的权重值在评价滑坡灾害分布上表现出共同的相关性，即分维值越大环境因子对滑坡地质灾害的影响越大，见表5。因此推断分维数可以用于表征滑坡地质灾害与环境因子之间在分形上的相关程度，分维数越大，则环境因子对滑坡地质灾害的影响越大，其敏感度排序为：高程>地层岩性>坡度>断裂缓冲区。

表5 不同评价模型的影响因素敏感性分级Table 5 Different factors evaluation model sensitivity rating

可见分形理论得出的滑坡灾害对不同影响因素的敏感性与逻辑回归模型、证据权模型、证据可信度函数模型、信息量模型所得到的结论具有很高的一致性，可以依此建立基于分形理论的滑坡灾害易发性评价模型。但是，由于分维模型的建立及分维数的求取与影响因子分类分级数目、分级方式和提取单元有很大的关系。不同精度的数据、不同的分级方法求取的计算结果可能会有较大差异，不同的区域由于环境特点不同，其结果也可能有很大差别。因此在建立分形评价模型时要严谨考虑这些问题。

5 结论

(1)云南省滑坡地质灾害的面积空间分布与坡度、高程、断裂缓冲区和岩性等环境因子呈现不同阶的变维分形特征，与断裂缓冲区和岩性呈2阶累计和变维分形，与高程呈3阶累计和变维分形，与坡度呈4阶累计和变维分形。

(2)分维数可以反映滑坡地质灾害与环境因子之间在分形上的复杂程度，其特征是分维数越大，则环境因子对滑坡地质灾害的影响越大。滑坡的影响因子敏感度的排序结果为：高程>地层岩性>坡度>断裂缓冲区。

(3)分形理论得出的滑坡灾害对不同影响因素的敏感性与逻辑回归模型、证据权模型、证据可信度函数模型和信息量模型所得到的结论具有很高的一致性，可以依此建立基于分形理论的滑坡灾害易发性评价模型。