实时演化地震定位方法及其不确定性分析

卢建旗，李山有，谢志南，马 强

(中国地震局工程力学研究所 中国地震局地震工程与工程振动重点实验室，黑龙江 哈尔滨 150080)

地震预警作为一种有效的减灾手段，已经在重大工程地震预警(如高速铁路、燃气管网、核电)以及城市地震灾害预警中得到了广泛应用[1,15-16]。地震预警的有效性在于其能够在地震发生后最短的时间内为预警用户提供反映地震破坏强弱或地震动大小的预警信息，使用户根据该信息采取相应的紧急处置策略。为了给预警用户提供尽可能多的预警时间，研究者希望地震预警系统能够在地震发生后最短的时间内(也就意味着利用尽可能少的信息)对该次地震的最终规模(震级及断层破裂尺度等)及其影响范围(地震动场或烈度场)做出准确估计。然而，利用少量信息获得的地震最终规模及其影响范围往往带有很大的不确定性[15]，例如：预警信息提供的估计工程场址的烈度为Ⅵ度，而真实场址的烈度可能为Ⅳ度，也可能为Ⅷ度。这种不确定性来源于场点烈度估计的每一个环节，如P波捡拾的误差造成震级估算的误差以及地震定位的误差，震级估算结果的不确定性，地壳速度结构的不确定性造成的定位方结果的不确定性，场点地震动参数估计的不确定性等等。这使得重大工程难以根据预警信息采取合理的紧急处置策略，极大地降低了地震预警的适用性。

与传统的地震定位方法不同，地震预警为了提高时效性的要求，定位方法主要依靠台站的P波走时信息进行定位。例如主站法[10], 该方法不需要地震发生的绝对时间，只要知道两个台站的P波到时就可以将震源限定在一个空间的双曲面内，随着触发台站的增多，形成了多个双曲面相交的情况，将震源位置限定在多个双曲面的交线或交点上，从而完成了地震定位。除此之外，还有双差定位法[6,17,18,21]，基于P波走时差分的最大似然估计定位方法[4,5]等。

利用已触发台站的走时信息进行定位只利用到了已触发台站的P波走时信息，而没有用到未触发台站的位置信息。而未触发台站可以将震中限定在一个更合理的范围内，不但可以提高定位的精度，还可以提高定位的效率。Horiuchi等[7,9,11,19-20]将未触发台站的信息成功运用到地震预警实时定位中，形成了“着未着”地震预警定位方法，从而很好地将未触发台站的信息运用到地震预警定位中。Rosenberger等[2]提出了基于高阶图以及P波到时顺序的定位方法(AOL)。金星等[12]在现有定位方法的基础上，提出了一种基于地震台网资料的网格化地震定位方法以及从单台触发到四台触发过渡的一套完整的地震预警连续定位方法[13-14,22]。Satriano等[3]在主站法及“着未着”方法的基础上，提出了一种等时差面与未触发台站信息相结合的概率定位方法。该方法很好地将两种方法进行了结合，并且，通过该方法能够提高定位概率。

目前，对于定位方法的不确定性概率模型还缺乏研究，在地震预警信息的不确定性分析中，缺乏关于地震定位的不确定性概率模型。

1 基于等时差面及未触发台站信息的实时演化定位方法

假设一次地震发生时，各个台站接收到P波到时均不存在误差，当有2个台站被地震触发后，利用2个台站的理论到时差与实际到时差可以将震源位置限定在空间的一个双曲面内，该双曲面即为等时差面(EDT)。当第3个台站触发后，利用3个台站两两到时差与理论到时差就可以将震源位置限定在3个双曲面的交线或交点上。当有更多台站P波到时信息后，震源位置就可以限定在空间一点(如图1(a))。这种定位方法称为等时差面法[10]。等时差面法的优点在于其不依赖于地震发生的绝对时刻，仅仅利用P波到时就可以进行地震定位。因此，在地震预警定位中得到了广泛应用。然而，各个台站的P波到时由于地壳速度结构的不确定性和P波到时识别结果的不确定性，会造成等时差面不相交的情况。为了增加更多的限定信息，人们想到了利用未触发台站的信息。假设某一局部平面内有如图1b所示的台站分布，该平面由均匀、各向同性介质构成，连接每两个台站构成线段的垂直平分线便可形成维诺图，维诺图将每一个台站划分在一个封闭的多边形区域内。在该平面内发生一次地震，如果有一个台站首先触发，则震源位于包含该台站的维诺图多边形内；如果两个台站同时触发，则震源位于包含两个台站的多边形公共边上，如果有三个台站同时触发则震源位于三个多边形的公共顶点上。Horiuchi将未触发台站的信息成功运用到地震预警实时定位中，形成了“着未着”地震预警定位方法，从而很好地将未触发台站的信息运用到地震预警定位中[7,9,11,19,20]

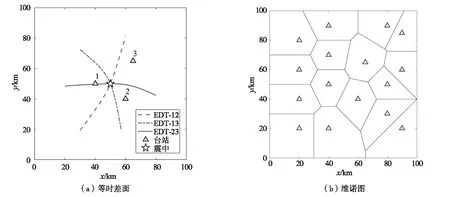
图1 等时差面与台站维诺图示意图Fig.1 Sketch map for EDT surface and Voronoi cells of seismic stations

基于等时差面及未触发台站信息的实时演化定位方法则是综合利用了已触发台站的到时信息和未触发台站的到时信息，建立了一种概率定位方法。

1.1 等时差面的概率表述

在不考虑走时误差和P波捡拾误差的条件下，当有两个台站被触发，则震源到两个台站的理论走时差与实际到时差应该相等(公式1)，则满足公式(1)的空间点组成了一个空间双曲面。每两个已触发台站的到时差都可以确定一个双曲面，随着触发台站的增多，震源位置被限定在多个双曲面形成的交线或交点上。

(ttm-ttn)i,j,k=tm-tn.

(1)

其中：m和n表示两个已触发台站的编号；tm和tn分别为台站m和台站n的P波实际到时；ttm和ttn分别表示震源位于空间网格点(i,j,k)处时，根据地壳速度结构计算得到台站m和台站n的P波理论到时。

然而，地壳速度结构具有不确定性，我们根据地壳速度结构计算的P波首波理论到时与实际观测到的P波首波实际到时差呈以均值为0，标准差为σ1的正态分布。因此，公式(1)可以写为：

(ttm-tm)±σ1-(ttn-tn)∓σ1=0.

(2)

同时，由于台站的实际到时是通过P波初至自动捡拾方法得到，P波真实到时与自动捡拾到时的残差呈均值为0，标准差为σ2的正态分布。因此，公式(2)可以进一步改写为：

(ttm-tm)±σ1±σ2-(ttn-tn)∓σ1∓σ2=0.

(3)

则根据独立同分布的规律，等时差面上的理论到时与实际到时差也满足正态分布：

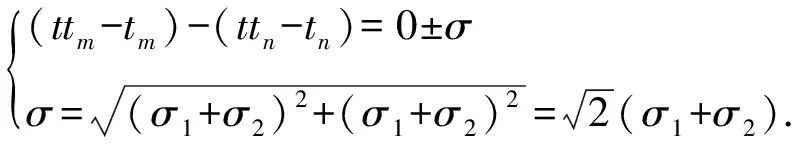
(4)

其概率密度函数的形式为：

(5)

(6)

由公式(6)可知，当实际到时差与理论到时差相差为0时，定位概率最大，随着差值变大，概率变小。对所有已触发台站进行两两组合，并在每个格点对所有台站对计算的概率求和可得等时差面总概率：

(7)

从概率理论的角度分析，在多个台站触发条件下，每个等时差面的概率密度函数在相互独立的条件下应为求积的关系而不是求和的关系。但在定位过程中，如果存在被噪声触发的台站，采用求积的形式会导致真实等时差面的概率被误触发台站在该处的低概率值所稀释，从而丢失真实震源位置，而采用求和的形式则不会出现这一现象。因此，这里每个空间网格点的总概率只表示了该点为震源位置的相对可能性大小，而不是绝对意义上的概率。

假设一共有N个台站参与定位，有nT个台站已触发，N-nT个台站未触发。则空间网格点处的等时差面概率最大值为：

Qmax=nT(nT-1)/2.

(8)

即，当只有一个台站触发时，没有等时差面，当有2个台站触发时有1个等时差面，以此类推。当每个触发台站的理论到时与实际到时差在等时差面上正好为0且多个等时差面能够恰好交于同一网格点，则该网格点的概率值恰好为等时差面概率的最大值Qmax。因此，等时差面概率值的大小能够体现定位过程中等时差面相交情况。

1.2 未触发台站控制范围的概率表述

如果利用台站分布建立的维诺图以及首个触发台站位置进行震源位置的空间限定，则存在维诺图边界的实时识别、误触发台站的处理等一系列技术问题。Horiuchi首次将未触发台站的限制思想引入到地震定位方法中，建立了“着未着”定位方法[7]。在“着未着”算法中，将未触发台站的走时与当前绝对时间之间建立不等式关系：

(ttl-ttn)i,j,k≥tnow-tn.

(9)

其中：l表示未触发台站的编号；n表示已触发台站的编号；tnow表示定位过程中的当前绝对时间；ttl和ttn分别表示震中位于空间网格点(i,j,k)处时计算得到未触发台站l和已触发台站n的理论到时；tn为已触发台站的实际到时。

未触发台站的约束不等式定义为概率的形式有：

(10)

即，当震源位于空间格点(i,j,k)处时，如果一个已触发台站n和一个未触发台站l的理论到时满足不等式(10)，则该格点为可能的震源位置，其概率值设定为1，否则设定为0。如图2(a)，图中有1个已触发台站(图中红色三角)，6个未触发台站(图中蓝色三角)，其余台站暂不考虑(灰色三角)。在首台触发时刻，利用1个已触发台站与6个未触发台站计算的可能为震源的区域是6条边界线(概率0、1边界)合围的区域，每个未触发台站与已触发台站计算的概率边界线正好在维诺图的边界上。随着时间的推移，边界线合围区域也在逐渐缩小(如图2(b))，即可能的震源区域在逐渐缩小。

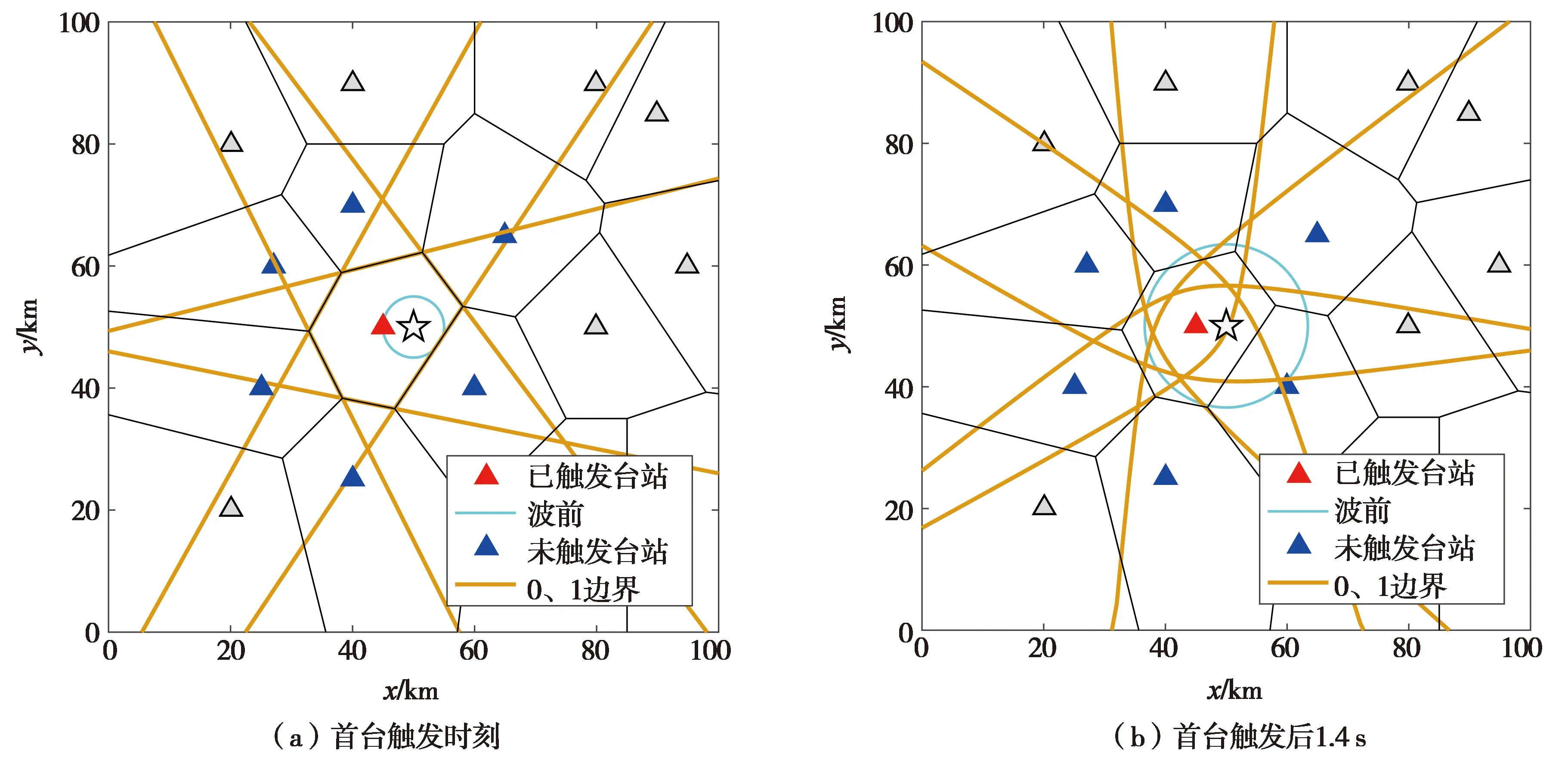
图2 随时间演化的维诺图示意图Fig.2 Sketch map for the evolutionary Voronoi cells

同样，为了避免误触发台站造成真实震源位置被误触发台站排除在外的可能，当有多个未触发台站和多个已触发台站时，利用每一对已触发台站和未触发台站计算每个空间网格点的概率Pl,n(i,j,k)，然后采用概率求和的形式计算该点的维诺图总概率PVoro(i,j,k)：

(11)

假设一共有N个台站参与定位，有nT个台站已触发，剩余N-nT个台站未触发，在无误触发台站的条件下，位于震源附近格点处维诺图总概率的最大值应为：

Pmax=(N-nT)nT.

(12)

即，在无误触发台站的条件下，由维诺图限定的震源可能区域内网格点处的维诺图概率最大值应为Pmax，其余区域格点上的维诺图概率均小于该值。

1.3 联合定位概率表述

为了让未触发台站形成的实时维诺图和已触发台站形成的实时等时差面在定位过程中同时起到限定震源位置的作用，将等时差面概率与维诺图概率在对应格点处相加得到每一个格点的联合定位概率R，并进行归一化：

(13)

通过搜索联合定位概率中的最大值即可找到震源所在的位置。归一化后的联合定位概率限定其值介于0到1之间，联合定位概率的大小反映了所有P波到时信息的吻合程度，概率值越大说明吻合程度越高，概率值越小说明吻合程度越低。在利用该值确定的震源点处，联合定位概率值为1，说明：(1)该点位于满足所有未触发台站限定的可能震源位置区域内；(2)该点位于所有已触发台站形成的等时差面相交的公共面、公共线或公共点上。联合定位概率值小于1说明：(1)该点可能位于未触发台站限定的具有相矛盾的区域，即部分未触发台站将该点确定为不可能震源位置点，而大部分未触发台站则将该点限定为可能的震源位置点；(2)所有已触发台站形成的等时差面可能并未完全相交于同一条线或者同一点。因此，联合定位概率值的大小客观反映了P波到时数据的不确定性大小，从而在一定程度上也反映了定位精度。但是，该概率值并非真正意义上的概率，而是一种表示震源位置可能性的相对值。

1.4 快速搜索方法

为了提高定位算法的效率，减少一次计算中网格格点的数量，本文采用了固定网格点数的网格间距缩小搜索方法，网格搜索的步骤如下：

(1)在定位算法中事先设定网格点数，当首台触发后，将网格中心点置于首台位置，网格大小可以设置到能够包含可能的震源区域，计算震源位于每个格点时的联合定位概率；

(2)搜索网格中最大概率值对应的网格格点，按照固定缩小倍数缩小网格间距，网格点数不变，然后将缩小后的网格中心置于概率值最大的网格点上，再次计算每个网格格点的概率；

(3)重复最大值搜索与网格间距缩小过程，直到网格间距缩小到可接受的程度。

以网格格点数5×5×5为例(如图3)，网格间距缩小倍数设为0.5。为了便于显示，本文仅展示了平面内网格搜索过程：

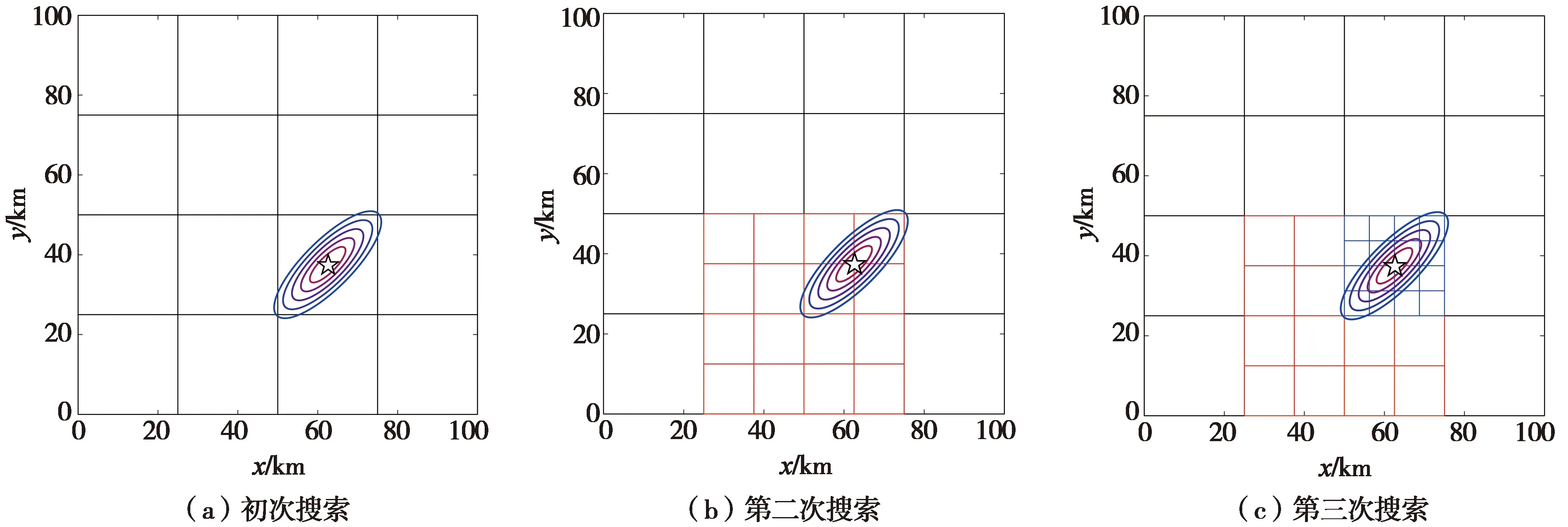
图3 网格搜索方法示意图Fig.3 Sketch map for grid searching

1)初次搜索时，将网格中心点置于第一个触发台站的位置，计算每个格点的概率。根据图3(a)中的概率等值线分布情况，最大概率可能位于空间坐标(50,25)处，也可能位于(75,50)处，假设自动搜索的最大值在(50,25)处；

2)将网格间距缩小到原来的一半，且将中心点置于(50,25)处(如图3(b))，再次计算缩小后网格点处的概率(即，红色网格格点处的概率)。根据图3b可知，本次搜索的最大概率位于网格点(62.5,32.5)处；

3)再次缩小网格间距，并将网格中心置于(62.5,32.5)处(如图3c)，计算缩小后网格点处的概率(即，蓝色网格格点处的概率)。依次循环，直到网格间距达到预先设定的最小值，定位结束。

这种搜索方法的优点在于其数组开销量小，不会在计算机内存中频繁改变内存地址，只需改变地址中的值，有助于提高效率。在实际定位过程中，如果网格缩小倍数太小，也会导致陷入局部极值的可能。因此，在实际计算过程中，可以适当增大网格间距缩小的倍数，使得定位结果更加可靠。本文采用了9×9×9的网格数，初始网格间距40 km，网格间距缩减倍数为0.8。

2 数据

为了让本研究中的定位不确定性能够更真实地反映实际台网分布以及实际地壳速度模型不确定造成定位结果的不确定性，本文选取了真实地震记录进行重新定位。由于中国强震观测台网数据目前没有绝对到时，为了满足这一要求，本文从日本K-NET强震观测台网中选取了能够涵盖2-9级的地震数据样本。其中网内地震204次，网外地震22次，震中分布见图4。由于定位的可靠性与台网的分布以及台网密度密切相关，本文计算了日本K-NET台网间距等值线图(如图5 所示)。结果显示，本文选取的日本K-NET台站的平均间距约25 km，最小台站间距可达2 km。该台站平均间距并不代表日本预警系统的台站间距，仅代表本文定位分析所用到的台站的平均间距。在本次定位不确定性分析中，没有考虑P波捡拾方法造成的P波到时拾取的不确定性，也没有考虑地震预警系统延时。定位过程中的P波到时使用了各个台站P波的实际到时，该实际到时通过人工判别方法进行拾取。P波的理论到时采用Crust1.0公布的速度结构进行首波到时计算。

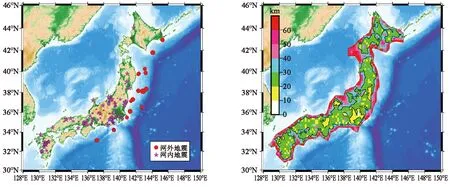
图4 震中分布图 图5 选取的日本K-NET台站间距等值线图

3 算例及结果

为了展示地震定位过程中等时差面概率以及未触发台站约束概率在定位过程中的变化情况，以及网内地震及网外地震定位概率的变化情况，本文选择了一次网内地震和一次网外地震。分别利用3台定位、4台、5台至8台对这次地震进行了定位计算。

选择的网内地震为2014年6月11日19时52分发生在日本东京附近的一次4.0级地震，震中位于135.685°E,35.085°N，震源深度10 km，共触发台站73个。定位过程中的定位概率分布图如图6所示。由图6可以看出，网内地震由于台站处于震中的四周，每两个已触发台站生成的等时差面与其余等时差面的相交角度较大，定位精度也高。同时，由于未触发台站也分布在震中的四周，能够有效将震源位置限定在一个很小的区域内，并且随着首播触发后时间的增加，未触发台站限定的震中位置也在不断缩小。在台站到时无误的情况下，3台就可以获得很高精度的定位结果。

图6 网内地震定位概率分布图Fig.6 Location probability distribution map for an inner-net event

选择的网外地震为2011年3月11日15时15分发生在日本东部海域的一次7.7级地震，震中位于141.265°E,36.108°N，震源深度43 km，共触发台站412个。定位过程中的定位概率分布图如图7所示。和网内地震相比，网外地震由于台站位于震中的一侧，而震中的另一侧无台站约束，形成的等时差面的交角也比较小，形成的相交区域大，定位精度低。同时，由于所有台站都分布在震中一侧，未触发台站不能将震中约束在一个封闭的区域内，而是只能约束在一个半封闭的区域内。因此，未触发台站的约束对定位所起到的效果有限。

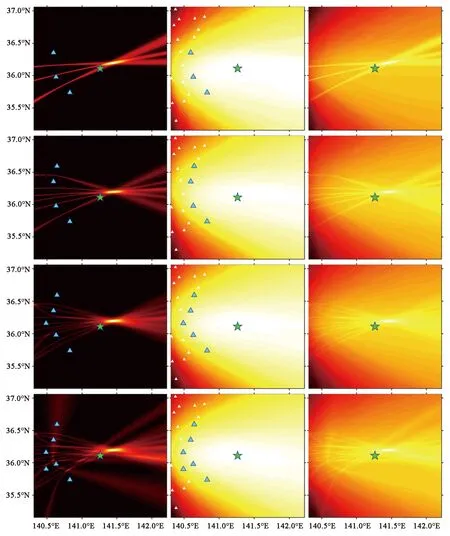
注：图中绿色五角星表示实际震中；蓝色三角形表示已触发台站；白色三角形表示未触发台站；第一列表示等时差面概率，第二列表示未触发台站约束概率，第三列表示联合概率。

利用该方法对本文搜集到的所有地震进行了重新定位，从定位残差与震级、网内地震、网外地震之间的分布情况(如图8)可以看出，定位残差的分布与震级的相关性较小，而与网内地震或网外地震的相关性较大。

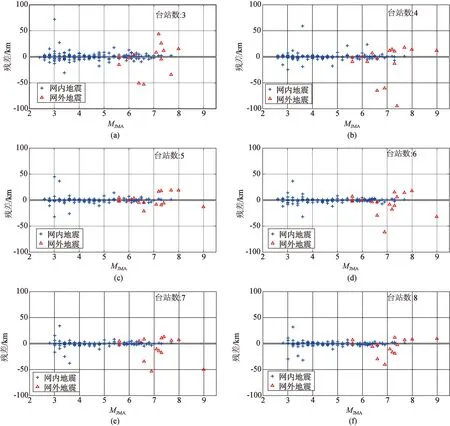
图8 定位残差随震级分布图Fig.8 Residual versus magnitude distribution map

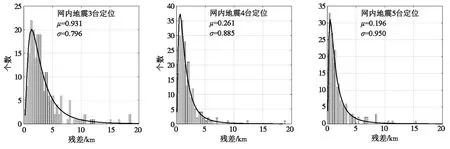
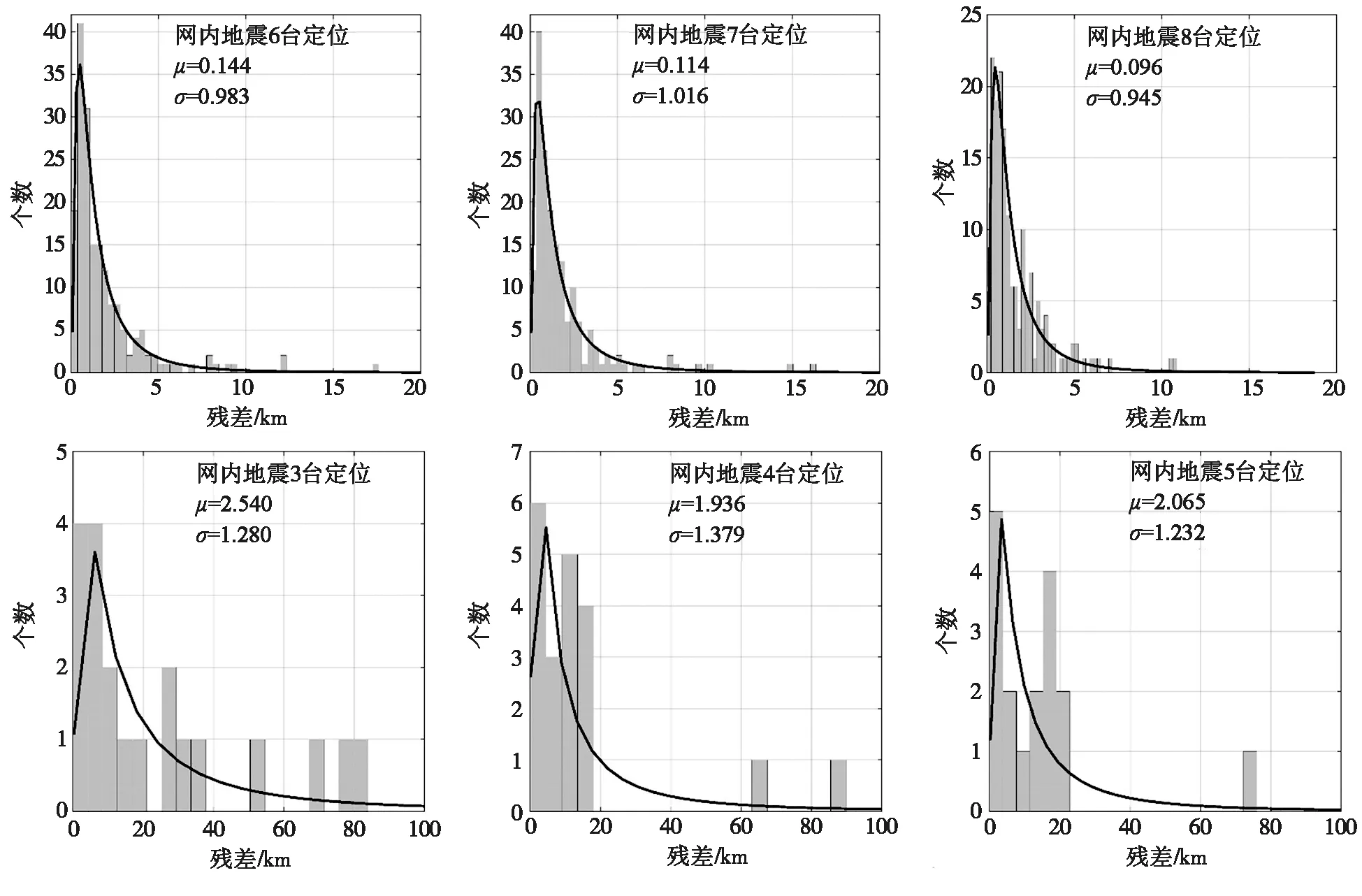
本文对定位残差的统计分成了网内地震和网外地震两组，定位残差如图9所示。每次地震分别采用了3台、4台、5台及8台定位。由图9可知，网内地震的定位残差普遍较小，网外地震的定位残差普遍较大，定位残差符合对数正态分布：

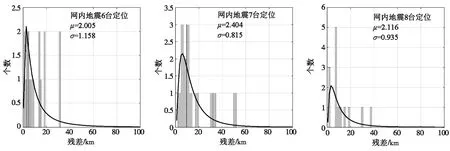
图9 定位残差分布图Fig.9 Distribution map of locating residuals

(14)

其中：x表示定位残差，取正值；μ和σ分别表示lnx的均值和标准差；f(x)表示对数正态分布的概率密度函数。

4 结论

地震预警定位结果的不确定性是地震预警信息不确定性的主要来源之一。为了分析地震预警定位的不确定性，本文选取日本K-NET台网记录到的204次网内地震及22次网外地震，利用地震预警系统中常用的地震定位方法——“实时演化地震定位方法”对这些地震进行了重新定位。结果表明，利用该定位方法获得的定位残差符合对数正态分布。网内地震的定位残差普遍较小，残差的均值在1～4 km之间；而网外地震由于台站分布在震中的单侧，造成等时差面相交角度较小，未触发台站不能将震中约束在一个封闭的区域内，从而导致定位残差普遍较大。由此可知，网外地震定位精度低也是预警参数不确定性分析中的一个不可忽视的因素。如果将网外地震的震中可能位置放在一个非常大的区域内进行考虑，则会因为震源位置变化太大而导致预警信息的不确定性增加，造成地震预警系统的实用性降低。我国东南沿海也存在大面积网外地震的发震构造。因此，如何提高网外地震的定位精度是地震预警应该考虑的问题。同时，如果地震预警系统能够识别网外地震，在此基础上，利用网外地震的定位方法[8]可能是解决这一问题的另一个途径。

本文选取日本K-NET台站的台站平均间距约25 km，与我国地震预警台网的密度较为接近。因此，该不确定性分析结果对我国地震预警系统定位不确定性有参考价值。

致谢：感谢日本K-NET强震观测台网为本文提供数据支持。