斜交简支梁桥地震位移响应特征与落座分析

杜 桁，徐略勤,2，邓海容，夏 雪，孙榕徽

(1.重庆交通大学 土木工程学院，重庆 400074； 2.重庆交通大学，省部共建山区桥梁及隧道工程国家重点实验室，重庆 400074)

近年来，我国桥梁建设事业飞速发展，桥梁数量日益增多。这其中，斜交梁桥因能更好地适应地形环境的差异性、改善道路的线形而得到广泛采用，尤其在地表崎岖的西部山区。然而，西部山区恰好与我国地震最活跃的断裂带相毗连，斜交梁桥由于其不规则的结构布置，地震响应远比正交桥复杂，损坏程度也更为严重。可见，高烈度地震给西部山区的斜交梁桥带来巨大的安全隐患。2008年汶川地震中的震害统计结果表明，斜交桥破坏比正交桥更为严重，有3/4的斜交桥都出现了中等以上震害[1]。斜交简支梁桥是汶川震区最为常见的斜交桥型，其典型震害特征表现为梁体水平移位和平面转动，部分桥梁甚至发生落座和落梁，伴随着主梁位移震害的还包括：板式橡胶支座滑移、撕裂、脱空、卷边；限位挡块挤裂、剪断、飞出以及伸缩缝错位、挤压变形、破坏等现象；而桥墩等下部结构出现结构性损伤的比例很低[2-3]。按照我国桥梁抗震设计规范[4]，斜交简支梁桥属于非规则桥梁，其抗震设计方法和抗震措施仍有待进一步完善。因此，研究这类桥梁在地震中的位移响应特征并进行落座分析具有重要的理论和工程参考意义。

近年来，国内外学者对斜交梁桥的地震响应和抗震性能已开展了不少研究，如Kun、Chen、陶源等[5-7]对斜交梁桥在伸缩缝和限位挡块处的碰撞效应或双向碰撞效应开展了数值模拟和试验研究；Kwon、闫聚考、陈彦江等[8-10]对简支斜交梁桥及正交桥主梁在地震作用下的平面旋转机理及碰撞效应进行了探讨；Noori、Jeon等[11-12]研究了地震输入方向和角度对斜交梁桥地震响应和抗震性能的影响，得到了很多富有启发的结论和成果。这些研究有力推动了斜交梁桥抗震理论和技术的进步，但不论是研究对象还是研究目的都各有侧重，在针对斜交简支梁桥地震位移响应特征与落座方面仍十分欠缺，尤其是对斜交桥主梁落座特点的研究亟待开展。震害调查经验表明，落座是桥梁最严重的震害表现之一，会中断桥梁上、下部结构的传力途径，使得桥梁在地震中成为不稳定的机构，防止桥梁落座是抗震措施设计的重要方面，我国桥梁抗震规范[4]对这方面的条文规定仍非常薄弱。有鉴于此，本文以我国公路桥梁中最为常见的30m跨斜交简支梁桥为研究对象，考虑桥梁结构中各种材料和接触非线性因素，基于参数分析探讨这类桥梁的地震位移响应特征，并结合斜交简支梁桥的结构特点，研究其主梁落座的特点和机理问题，以期为这类桥梁的抗震设计和加固提供参考。

1 典型桥例与分析模型

1.1 桥例概况

结合汶川震害资料[1]，以我国高速公路上最为常见的30 m斜交简支T梁桥作为研究对象。如图1(a)所示，为了考虑边界跨的影响，分析桥例的跨径布置为5×30 m，主梁由5片C50预应力混凝土T梁组成，桥宽12.5 m，基本工况下主梁斜交角为30°。每片T梁的两端各设置1个GYZ D300×96板式橡胶支座。双柱圆墩高15 m，直径为1.8 m，墩柱顶设盖梁，盖梁两端设钢筋混凝土限位挡块，墩柱和盖梁均采用C35混凝土，墩柱纵筋为30根HRB40028热轧钢筋，箍筋采用HRB40010光圆钢筋。桥墩基础采用桩柱式基础，桩径为2.0m，桥例平面和断面布置详见图1(b)和(c)。

图1 桥例布置(单位：cm)Fig.1 Bridge layout(Unit：cm)

1.2 分析模型

采用SAP2000程序建立有限元模型，斜交主梁按照梁格法模拟，其中，T梁采用线弹性梁单元模拟，T梁间的横向联系采用虚拟梁单元模拟，纵梁与虚拟横梁形成斜交网格，如图2(a)所示。盖梁采用线弹性梁单元模拟，与墩柱间采用刚接。桥墩为延性构件，可能进入塑性状态，对于框架墩来说墩顶和墩底均为潜在塑性铰区，因此采用PMM纤维铰来定义塑性铰的特性，并按照现行规范[4]确定塑性铰长度及其位置，如图2(b)所示。本文研究对象为西部山区斜交简支梁桥，所处地质条件一般较好，而且根据规范，中小跨径梁桥的桩-土相互作用可忽略。因此，为了不给分析工作引入过多的不确定性，本文不考虑桩柱基础的非线性行为，直接将墩底固结。

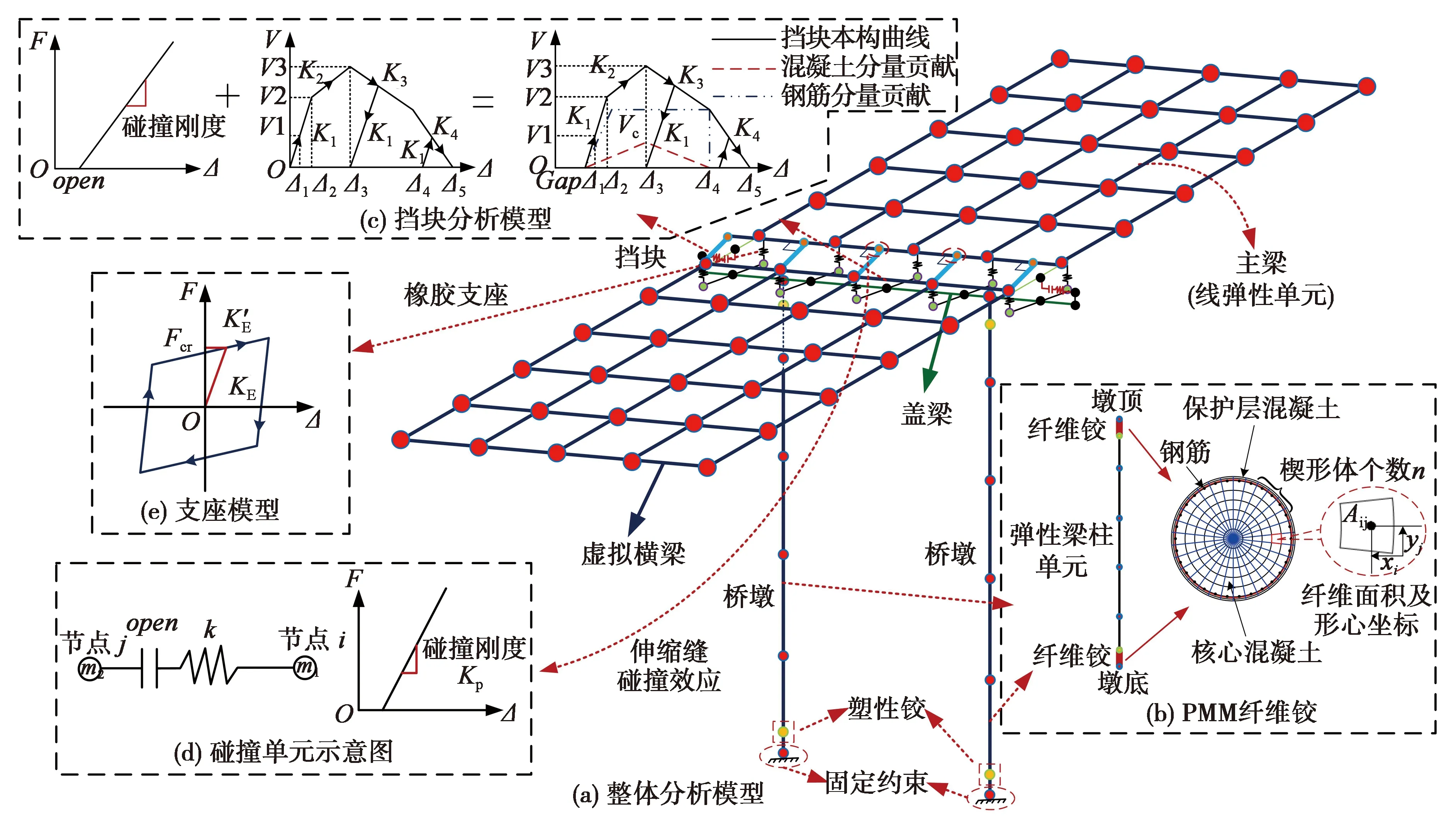
图2 分析模型Fig.2 Analytical model

汶川震害显示，限位挡块对主梁地震位移响应的影响很大，因此模型中必须加以考虑。根据文献[13]的研究，采用Multi-linear Plastic单元模拟其简化滞回模型，并与Gap单元串联来模拟挡块与主梁间的碰撞现象，初始间隙为0.02m，如图2(c)所示。

为了考虑梁体可能的平面旋转，在梁端伸缩缝处设置5个碰撞单元，碰撞单元采用Gap单元的合并/张开来激活/钝化邻梁之间的碰撞作用，如图2(d)所示。碰撞刚度参考Muthukumar等[14]的研究取主梁的轴向刚度，本文桥例为Kp=1.074×106kN/m，伸缩缝的初始间隙为0.1 m。

水平向刚度：

Kh=nGbAr/∑t

(1)

竖向刚度：

Kv=nEbAr/∑t

(2)

转动刚度：

Kr=0.5nEbIb/∑t

(3)

式中：n为支座个数；Gb为支座剪切模量，根据规范[4]取1 200 kN/m2；Ar为支座橡胶板面积；∑t为橡胶层总厚度；Eb为支座竖向抗压模量；Ib为支座沿弯曲方向的惯性矩。

1.3 分析工况

根据汶川震害调查统计情况[1]，选择斜交简支梁桥上部结构地震位移响应的关键影响因素：斜交角、挡块强度和伸缩缝大小作为研究参数。其中，斜交角是主梁平面旋转的重要影响因素[8-9]；挡块强度是挡块约束板式橡胶支座滑动行为的关键因素[13]；而伸缩缝大小则影响着相邻梁体碰撞效应的程度[6-7]。表1列举了本文参数分析的工况设置情况，其中，基准模型的斜交角为30°、挡块强度取各墩恒载支反力的10%、支座摩擦系数取0.15、伸缩缝大小取0.1 m，其余各工况均在此基础上改变其中一个参数的取值。

表1 分析工况设置Table 1 Details of analytical cases

1.4 地震动输入

选取7组实际近场地震波，每组地震波包含2条水平向和1条竖向地震加速度记录，如表2所示。为了方便对数据进行对比分析，将7组地震波中水平向最大峰值加速度PGA统一调整至0.4 g，其余2个方向的地震波按照相同的调幅系数进行调整。在进行非线性时程分析时，地震加速度时程波沿着桥梁的纵+横+竖三向输入，其中沿桥梁纵向输入每组地震波中水平向PGA较大一条的加速度时程。

表2 地震波基本信息Table 2 Basic information of seismic records

2 地震位移响应特征分析

2.1 考虑斜交角的位移响应分析

图3以No.2地震波为例给出了3#桥墩上右跨中支座纵、横向力-位移响应曲线随斜交角的变化情况。由图3(a)～(b)可知，支座沿着纵、横向都发生明显的滑动行为，这种行为可以限制主梁地震惯性力向下部墩柱的传递，从而保护墩柱免遭结构性破坏，但同时也会导致主梁位移显著增大；在纵桥向，当斜交角为30°时，支座滑动位移最大，而在横桥向，当斜交角为60°时，支座滑动位移最大。由图3(c)可见，以7条波的平均值来看，随着斜交角的增大，支座纵向最大滑动位移先增后减，在斜交角为30°时出现最大值20.5 cm，在斜交角为60°时出现最小值5.8 cm，两者相差71.7%；支座横向最大滑动位移则先减后增，在斜交角为30°时出现最小值5.1 cm，在斜交角为60°时出现最大值24.4 cm，两者相差79.1%；两个方向的位移响应表现出明显的耦合特征。

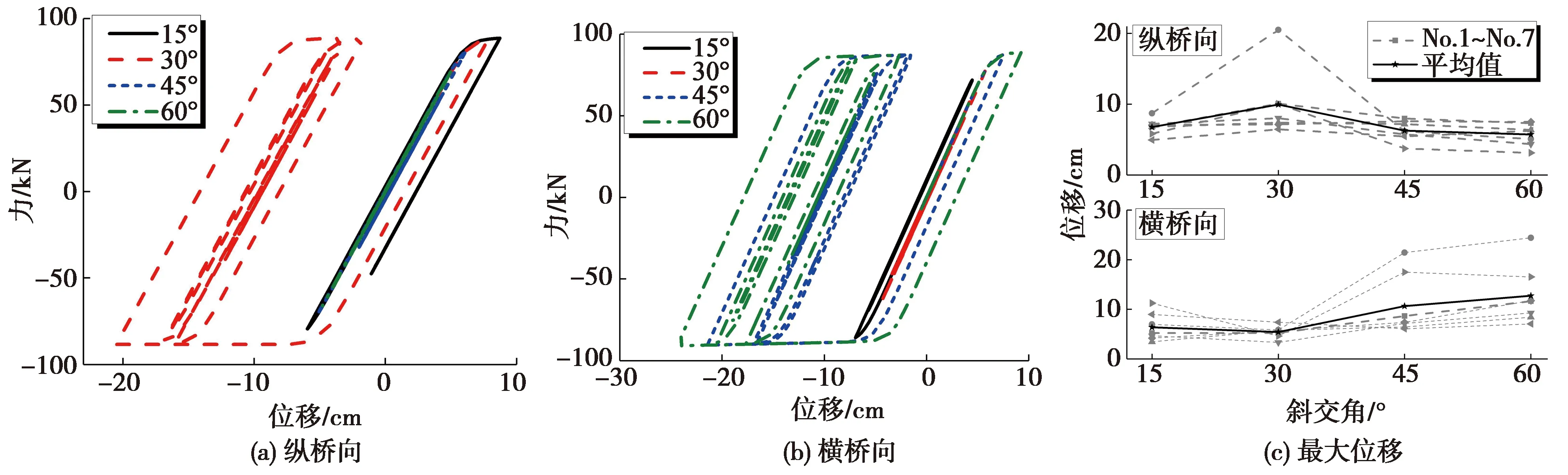
图3 斜交角对支座位移的影响Fig.3 Effects of skew angles on bearing displacement

图4以No.3地震波为例给出了第3跨(如图1所示)左侧梁端纵、横向位移响应时程随斜交角的变化情况。由图可知，斜交角对梁端最大位移和残余位移影响很大，随着斜交角的增大，梁端最大纵向位移出现波动变化，当斜交角由15°增至30°时，梁端最大纵向位移由19.3 cm减为6.9 cm，减幅达到12.4 cm；梁端最大横向位移则先增后减，当斜交角由15°增至30°时，梁端最大横向位移由3.6 cm增至19.7 cm，增大了16.1 cm，之后再减小；可以看到梁端纵向位移的减少量与横向位移的增加量较为接近。梁端最大纵向残余位移先增后减，最大横向残余位移则先减后增。与支座位移响应相对应，主梁梁端位移在纵、横向也表现出明显的耦合特征。

图4 斜交角对梁端位移的影响Fig.4 Effects of skew angles on girder end displacement

图5为第3跨主梁平面转角包络值随斜交角的变化情况。可以看到，主梁平面转角在不同地震波作用下的变化规律有所不同。但以平均值来看，随着斜交角的增大，主梁平面转角先增后减，在斜交角为30°时达到最大值。在斜交角为15°～60°范围内，主梁平面转角平均值的变化范围为1.318×10-4rad～31.6×10-4rad，最大值是最小值的23.9倍。

图5 斜交角对主梁平面转角的影响Fig.5 Effects of skew angles on girder rotations

综合图3～图5的规律可以发现，斜交角大小是桥梁上部结构位移响应特征的重要影响因素。当斜交角小于30°时，支座纵向力-位移曲线出现了明显的滞回环，滞回曲线相较于斜交角为45°和60°时更饱满，且此时主梁梁端纵向残余位移也明显大于45°和60°时的残余位移，表明在斜交角为30°时支座的纵桥向滑动行为最显著，即：当斜交角小于30°时，上部结构的位移响应主要以纵桥向为主，且在30°时位移达到最大值。当斜交角大于30°后，支座纵向力-位移曲线几乎呈线性，但在横向却发生了明显的滑动行为，且梁端残余位移在横向上明显更大，由此说明当斜交角大于30°后，上部结构的位移响应主要以横桥向为主，且在60°时达到最大值。这一特征可为斜交简支梁桥地震位移控制措施提供方向。

2.2 考虑挡块强度的位移响应分析

图6以No.2地震波为例给出了3#桥墩上右跨中支座纵、横向力-位移响应曲线随挡块强度的变化情况。由图6(a)～(b)可见，支座在纵向仍然发生了滑动行为，但随着挡块强度的增大，其滑动位移逐渐减小；而支座在横向则几乎没有产生滑动行为，表明合理设计挡块的强度具有良好的位移控制效果。而且与正交桥不同的是，在斜交简支桥中，挡块的限位效果不仅对支座的横向位移响应有限制作用，对支座纵向响应也有较好的约束效果，其原因在于前文提及的斜交桥纵、横向地震位移的耦合效应，以及挡块对主梁平面转动的约束作用，这点后文会有进一步分析。由图6(c)可见，以7条波的平均值来看，随着挡块强度的增大，支座纵、横向位移均逐渐减小，其中纵向位移的最大降幅为15.53%，横向为9.33%，且横向位移平均值显著小于纵向。值得一提的是，当挡块强度达30%恒载支反力时，支座纵、横向位移曲线趋于平缓，表明当挡块强度达到某一数值时，其对支座滑移位移的约束作用已趋于最大效果，此时不宜使用强度更大的挡块，而应结合下部墩柱的损伤程度来确定挡块合理的强度，因为挡块也会将主梁的部分惯性力传递给下部墩柱。

图6 挡块强度对支座位移的影响Fig.6 Effects of retainer capacities on bearing displacement

图7以No.2地震波为例给出了第3跨左侧梁端纵、横向位移响应随挡块强度的变化情况。由图可知，梁端最大位移随挡块强度的增大略有下降，但总体上降幅较小，其原因在于梁端位移由支座位移和墩顶位移组成，挡块可以降低支座的位移，但同时因向墩柱传递主梁惯性力而导致墩顶位移有所增大，两者相互抵消，使得挡块的限位效果在梁端位移响应上无法体现。梁端纵向残余位移随挡块强度的增大而减小，横向残余位移随强度增大而先增后略减，但总体上呈减小的规律。

图7 挡块强度对梁端位移的影响Fig.7 Effects of retainer capacities on girder end displacement

图8为第3跨主梁平面转角包络值随挡块强度的变化情况。以平均值来看，挡块强度的增大可以有效地降低主梁的平面转动，如当挡块强度为10%恒载支反力时，主梁平面转角平均值为23.27rad，当挡块强度为50%恒载支反力时，主梁平面转角平均值为16.73rad，下降28.12%。同样可以看到，在本文桥例中，当挡块强度达到30%时，主梁平面转角的下降趋势已明显减缓，即挡块的限制作用已经达到最高效果，表明挡块强度并非越大越好。

图8 挡块强度对主梁平面转角的影响Fig.8 Effects of retainer capacities on girder rotations

2.3 考虑伸缩缝大小的位移响应分析

图9以No.2地震波为例给出了3#桥墩上右跨中支座纵、横向力-位移响应曲线随伸缩缝大小的变化情况。相比斜交角和挡块强度，伸缩缝大小对支座地震响应的影响要小得多，其原因可能与碰撞效应有关。伸缩缝大小会影响邻梁碰撞程度，但由于主梁会同时受到左右两侧相邻主梁的碰撞，在两侧碰撞效应接近的情况下，碰撞程度(伸缩缝大小)对支座地震响应的影响可能会被抵消。由图9(a)～(b)可知，支座在纵桥向虽也发生了明显的滑动行为，但随伸缩缝大小的增大，其滑动位移几乎没有变化；而支座在横桥向没有产生滑动行为，位移响应略有下降。由图9(c)可见，以平均值来看，随着伸缩缝大小的增大，支座纵、横向最大滑动位移略有减小，纵向最大位移由7.72cm降至7.40cm，横向最大位移由8.55cm降为6.20cm。支座位移随着伸缩缝增大反而下降的趋势可能与所选支座位置和碰撞效应有关。由于同一桥墩处横向各支座的位移响应有明显区别，限于篇幅且便于后文落座分析，本文选取了横桥向的中间支座(即主梁重心线处的支座)来说明各研究参数对支座地震响应的影响。为了进一步探讨伸缩缝大小的影响，后文将专门分析碰撞效应的变化情况。

图9 伸缩缝大小对支座位移的影响Fig.9 Effects of expansion joint size on bearing displacement

图10以No.2地震波为例给出了第3跨左侧梁端纵、横向位移响应随伸缩缝大小的变化情况。由图可知，随着伸缩缝间距的增大，梁端纵、横向最大位移均增大，其中横向最大位移先减而后增，但总体呈增大趋势；梁端纵、横向残余位移也随伸缩缝大小的增大而增大。这是由于伸缩缝大小的增大在纵桥向上为主梁提供了更大的位移空间，而斜交主梁的位移耦合效应使得梁端横向位移也同时有所增大。

图10 伸缩缝大小对梁端位移的影响Fig.10 Effects of expansion joint size on girder end displacement

在7组地震波下，各伸缩缝处的碰撞效应呈相似的变化规律，为便于讨论，以No.1地震波的分析结果为例进行讨论。图11为4#墩上伸缩缝处的碰撞力分布的变化情况，由图11(a)可见，同一伸缩缝处的碰撞力在横桥向分布是不均匀的，越靠近桥面中心线越小，甚至为零，伸缩缝横向两侧角点处的碰撞力则明显更大，其原因在于斜交主梁在地震中产生了平面转动，两个角点处最容易与邻梁发生接触，因此最容易产生碰撞力，且两个角点处的碰撞力本身也不相同。图11(b)、(c)分别给出了1#和5#碰撞单元的碰撞力时程，可以看到，1#单元的最大碰撞力为1 668.86kN，而5#单元的最大碰撞力达4 457.74kN，是1#单元的2.67倍，且两者出现的时间不同步。由于碰撞力是与位移正相关的，因此斜交主梁在地震中更容易沿着自身锐角端向桥面内发生转动，而这种转动又反过来增大了伸缩缝处不均匀的碰撞力分布，使主梁在伸缩缝处表现出“碰撞→增大转动→不均匀碰撞力增大→转动加剧”的循环过程。从伸缩缝大小的影响来看，同一伸缩缝处的碰撞单元表现出不同的规律，1#单元碰撞力随着伸缩缝的增大而逐渐增大，增幅为39.7%；5#单元碰撞力随着伸缩缝的增大而先减后增，最大值和最小值相差20.3%。从各单元碰撞力峰值来看，由于斜交桥存在不均匀碰撞现象，在本文的研究范围内，伸缩缝为8cm时，碰撞力峰值是最小的。

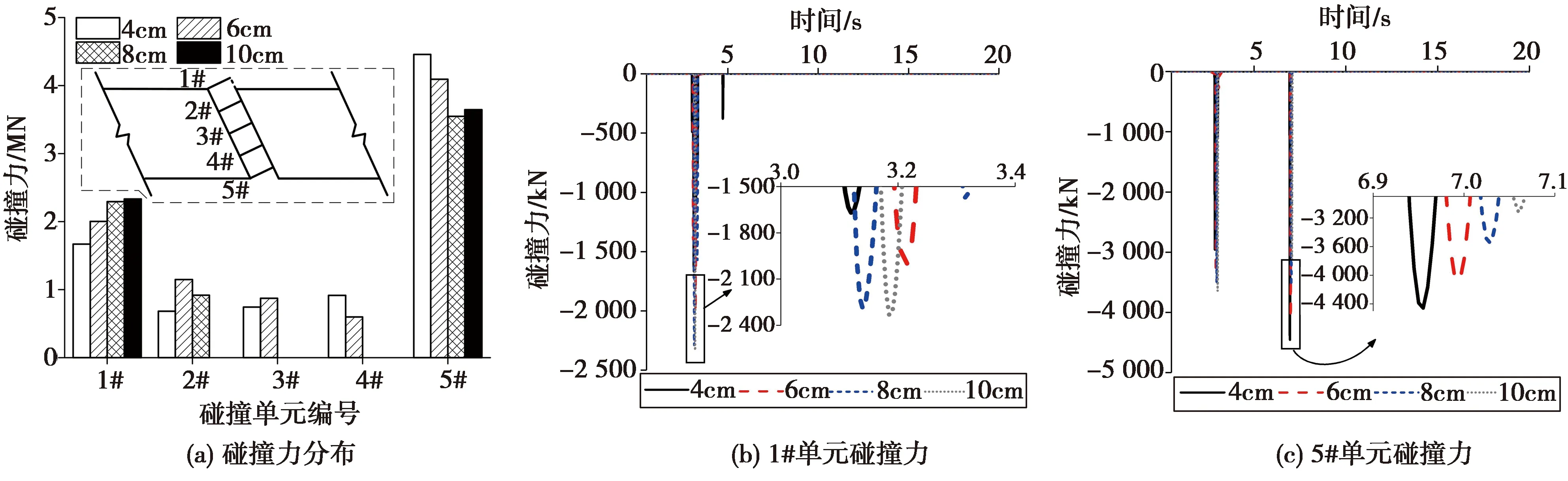
图11 伸缩缝大小对碰撞力的影响Fig.11 Effects of expansion joint size on pounding forces

3 落座分析

前文分析表明，支座在地震中会发生滑动行为，若滑动位移过大则会导致主梁落座。实际工程中若主梁发生落座，则支座的传力途径将会被中断，支座的滑动摩擦本构模型不再成立，但这个过程在数值模拟中很难精确实现。在主梁落座之前，一般可认为支座的本构模型是合理的[15]，因此从数值模拟的角度分析落座是可能的，但分析落梁则存在一定的困难，因为落梁往往发生在落座之后。图12和表3给出了支座滑动状态的判断依据[16]，其中，D为支座与上部结构之间的相对位移；D0为支座的滑动临界位移，D0=μ·N/Kh，符号意义同前文；D1为初始时刻梁底钢板内边缘至支座内边缘的距离；D2为梁底钢板内边缘至支座中心线的距离；D3为梁底钢板内边缘至支座外边缘的距离。

图12 支座滑动状态示意图Fig.12 Diagram of the slide states of bearing

根据表3的指标，对前文各工况下的支座纵、横向位移状态进行分析，表4列举了在No.2、No.5和No.7三组典型地震波作用下，3#墩上右跨中支座的滑动状态，表中仅列出滑动更严重的那个方向的结果，并将“纵向轻微滑动”简称为 “轻滑-纵”，其他表述类似。

表3 支座滑动状态指标Table 3 Indexes of the slide states of bearing

表4 支座滑动状态结果Table 4 Results of the slide states of bearing

由表可知，当斜交角为15°～30°时，支座在纵向上产生更明显的滑动行为；当斜交角为45°～60°时，支座的滑动方向逐渐转为横向。这与前文所述规律相符，即：当斜交角小于30°时，上部结构位移响应以纵向为主，当斜交角大于30°时则相反。地震作用下，斜交主梁的一端会与邻跨抵紧，另一端则更易摆动，结构地震响应类似于循环荷载作用下的“棘轮效应”[17]，斜交角的增大加剧了摆动程度，使得支座在斜交角大于30°时横向滑动更明显。当挡块强度由10%恒载支反力升至50%时，大多数地震波下的支座滑移程度由严重/中等降低为轻微滑动；且在挡块强度大于30%之后滑动程度不再改变。几乎所有地震波作用下的支座都发生纵向滑动，横向几乎不发生滑动或滑动程度很低，表明了挡块的限位作用十分显著，适当增大挡块的强度可有效减轻支座的滑动状态。伸缩缝大小对支座滑动状态的影响并不显著，在大多数地震波作用下伸缩缝大小并没有改变支座的滑动状态，但在个别地震波(如No.7)下，增大伸缩缝大小可在一定程度上减轻支座的滑移程度。值得一提的是，在本文的研究范围内，中间支座并没有出现落座情况(由于中支座位于主梁重心线上，主梁因此一般也不会出现落梁情况)。

图13选取3个典型工况分析了斜交简支梁桥第3跨主梁的位移响应特点，图中支座的颜色与表4表示相同的滑动状态。由图可知，由于主梁发生平面转动，各支座的滑动状态有所不同，且在不同的斜交角和挡块强度下，支座纵、横向滑动的严重程度会发生转换，但基本都存在如下趋势：即斜交主梁在地震中更容易沿着自身锐角端向桥面内发生转动，按照图中的示意方向即逆时针转动。因此，在实际工程中可以适当加强锐角端的挡块强度，减轻主梁的平面转动幅度，降低落座风险。

图13 斜交简支梁位移响应特征Fig.13 Displacement features of simply-supported skewed girder

4 结论

本文主要结论如下：

(1)斜交简支梁桥的地震位移响应具有明显的纵、横向耦合特征，当斜交角小于30°时，位移响应以纵向为主，且在30°时达到最大值；当斜交角大于30°后，位移响应以横向为主，且在60°时达到最大值。主梁平面转角随着斜交角的增大而先增后减，在斜交角为30°时达到最大值。

(2)挡块不仅可有效制约支座的横向位移，对支座纵向位移也有较好的约束效果，随着挡块强度的增大，支座纵、横向位移以及主梁平面转角均逐渐减小，但当挡块强度达到某一数值时，其限位效果会逐渐趋于平缓，因此挡块强度并非越大越好。本文桥例中，当挡块强度达到30%恒载支反力时，其限位效果可达最优。

(3)斜交简支梁桥在伸缩缝处存在不均匀碰撞现象，两侧角点处的碰撞力明显更大，靠近桥面中心线处碰撞力最小甚至为0，不均匀碰撞使得斜交主梁容易沿着自身锐角端向桥面内发生转动。

(4)本文桥例未出现落座情况，但出现大量严重滑动(即主梁与支座半脱空状态)的工况，且随着斜交角的增大，支座的滑动方向逐渐由纵向转为横向。伸缩缝大小对支座滑动影响很小，但适当增大挡块的强度(尤其是适当加强斜交主梁锐角端的挡块强度)可有效减轻支座的滑动状态。