基于切比雪夫不等式地震人员伤亡评估

王 野，于建杰，余世舟

(中国地震局工程力学研究所，中国地震局地震工程与工程振动重点实验室，黑龙江 哈尔滨 150080 )

我国是一个破坏性地震频发的国家，近几十年来随着经济的高速发展，财富集中、人口密集，地震风险增加，为减少地震造成的损失，开展震害预测工作对地震预防和震后应急尤为重要。其中，地震人员伤亡评估结果是震前预防和震后应急工作的重要参考依据[1-7]。

对比国内外已有研究成果，地震人员伤亡的评估方法，按照结果表达方式来分，则主要分为两类，其一是给出地震造成人员伤亡的期望值，如国外的Samardjieva等学者[8]根据1990年以来的全球范围内的地震震害人员伤亡统计数据，回归分析得到的基于全球尺度下的人员伤亡和震级之间的公式，给出在不同震级下人员伤亡的期望值；国内的肖光先[9]以房屋破坏间数作为主要参数，并同时考虑相对人口密度的影响，总结得出近似的人员伤亡期望值经验计算公式；刘吉夫等[10]收集了大量国内破坏性地震的数据，并考虑了死亡率为0时的特殊情况，拟合给出新的地震人员伤亡期望值评估模型；郑山锁、张睿明等[11]在考虑了不同时段人员在室率、人员密度以及不同结构类型破坏下人员伤亡率的情况下，给出了地震伤亡评估模型，并通过算例验算，验证其评估模型的合理性和正确性。其二是给出地震造成人员伤亡数在某一范围内的概率，如李帆等[12]考虑了人员密度、在室率和结构不同破坏状态下人员死亡率，通过运用中心极限定理，给出了在不同给定预测概率下的死亡人数上限；USGS于2007年发布的全球地震快速评估系统PAGER[13],在人员损失评估方面，给出基于历史震害数据回归分析得到的经验评估模型，从而得到人员伤亡数落在某两个阈值间的概率。

总结人员伤亡评估方法现状可发现，有些评估方法虽然考虑到了建筑结构易损性对伤亡的影响，但其往往只能给出人员伤亡的期望值，由于实际房屋建筑的震害表现具有很强的不确定性，单一的期望值估算不能充分评估描述震害损失的不确定性。还有些评估方法虽然能给出某一人员伤亡范围的概率，但多是基于历史伤亡数据的统计分析结果给出的，未考虑区域建筑结构易损性差异。

因此，本文基于建筑结构易损性，采用切比雪夫不等式分析结构震害的不确定性变化范围，给出地震人员伤亡评估结果的变化函数。并结合算例对比分析评估方法的适用性。

1 震害分布趋势

建筑结构易损性结果通常以易损性曲线或震害矩阵的形式给出。将建筑结构不同的破坏等级按照震害指数进行划分，将各破坏等级对应的震害指数范围中值作为横坐标，各破坏等级的概率为纵坐标，则可得到在不同烈度下各破坏等级比例的散点图，并将散点用平滑的曲线进行连接，令其与正态函数曲线对比可发现，其分布趋势近似服从截断正态分布。现以某地的单层房屋震害矩阵为例做对比图，如图1及表1所示。

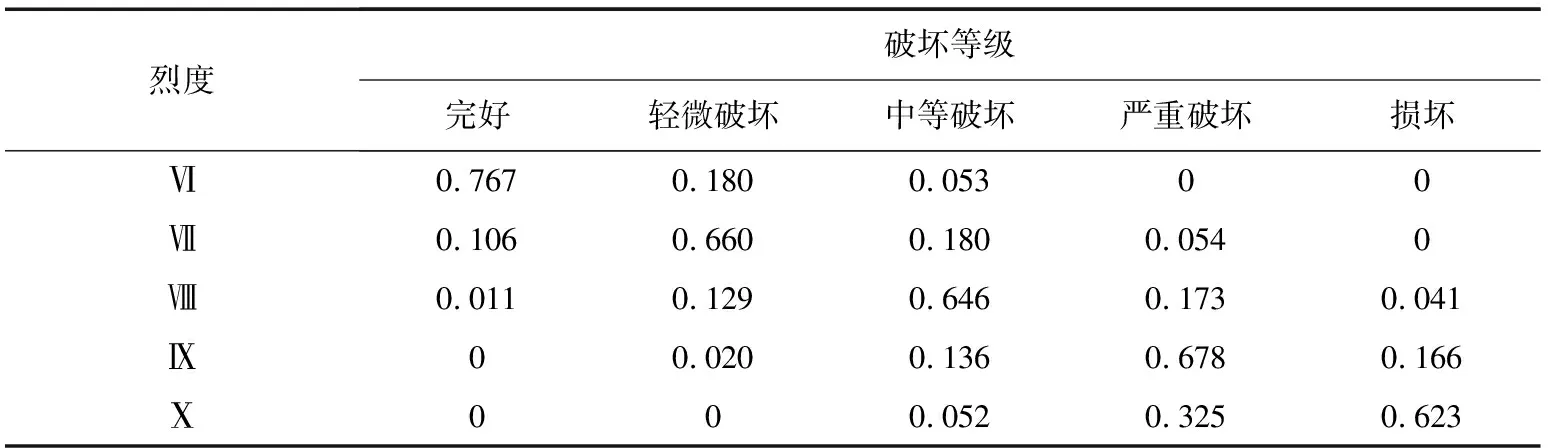
表1 某地单层房屋震害矩阵Table 1 Earthquake damage matrix of a single-story building in a certain area

图1 各烈度下震害指数-概率散点图与正态函数曲线趋势图对比图Fig.1 Comparison of seismic damage index-probability scatter plot and normal function curve trend graph under different intensity

2 基于切比雪夫不等式的范围限定

基于震害分布趋势及切比雪夫不等式对分布函数曲线各区间的概率估计方法，可给出各破坏等级可能的比率限定范围。

首先根据1中震害分布趋势所述可知某一烈度下各破坏等级比例曲线分布趋势近似服从截断正态分布，则可根据易损性曲线或震害矩阵，以不同破坏等级对应的震害指数为横坐标，各破坏等级的概率为纵坐标，进行正态分布拟合，给出正态分布函数N(μ,δ2)。则震害分布为N(μ,δ2)/P{0≤X≤1}在[0～1]间的截断部分。

其次基于切比雪夫不等式可计算出各破坏等级的比例上限，计算见下式(1)。

(1)

式中：P{0≤X≤1}为正态函数N(μ,δ2)在[0～1]间的概率；K为破坏等级比例约束上限；ζ1、ζ2分别为破坏等级对应的震害指数范围的两个边界值到均值μ的距离，如K为建筑物基本完好比例约束上限，则ζ1、ζ2为基本完好对应的震害指数范围的两个边界值到均值μ的距离。

3 不确定性的评估方法

基于建筑结构易损性，考虑人员在室率、各破坏等级对应的经验伤亡率，即可估算因建筑破坏而导致的人员伤亡。

根据前文切比雪夫不等式约束后的各破坏等级比例变化范围，即可给出地震造成人员伤亡最值。其中伤亡人数最小值Dmin计算方式为：令约束后的各破坏等级比例变化范围按照完好、轻微破坏、中等破坏、严重破坏、损坏的顺序依次在变化范围内取上限值，至比例累计到1时停止后续破坏等级的取值(即计算最小值时在各破坏等级比例和为1的前提下，令建筑结构尽可能处在破坏程度轻的等级)，同时考虑人员在室率、各破坏等级对应的经验伤亡率，即可估算因建筑破坏而导致的人员伤亡最小值Dmin。同理对于最大值Dmax的计算方式为：令约束后的各破坏等级比例变化范围按照损坏、严重破坏、中等破坏、轻微破坏、完好的顺序依次在变化范围内取上限值，至比例累计到1时停止后续破坏等级的取值(即计算最大值时在各破坏等级比例和为1的前提下，令建筑结构尽可能处在破坏程度严重的等级)，同时考虑人员在室率、各破坏等级对应的经验伤亡率，即可估算因建筑破坏而导致的人员伤亡最大值Dmax。

ATC-13方法中假定专家意见的结果按照对数正态分布，并按照专家给出的最大和最小值构成90%的置信区间，给出各烈度地震破坏损失率的对数正态分布[14]。本文借鉴ATC-13方法给出损失率分布函数的研究思路，以正态分布函数距均值处3倍标准差距内构成约99.7%为置信区间，给出人员伤亡分布函数曲线。其中以伤亡人数最大值Dmax最小值Dmin对数均值近似作为函数均值μD，计算见式(2)，按照满足置信区间约为99.7%的要求，以6倍标准差距离为限值求出函数标准差δD，如式(3)所示，进而给出变化函数及趋势图。

μD=(lg(Dmax)+lg(Dmin))/2.

(2)

δD=(lg(Dmax)-lg(Dmin))/6.

(3)

4 算例分析

基于某城市震害预测的基础信息，以多层砌体房屋为例，对上述方法进行算例分析。该城市多层砌体房屋震害矩阵如下表2所示，给出该城市多层砌体房屋各烈度下的对数死亡人数函数曲线的过程为以下几步：

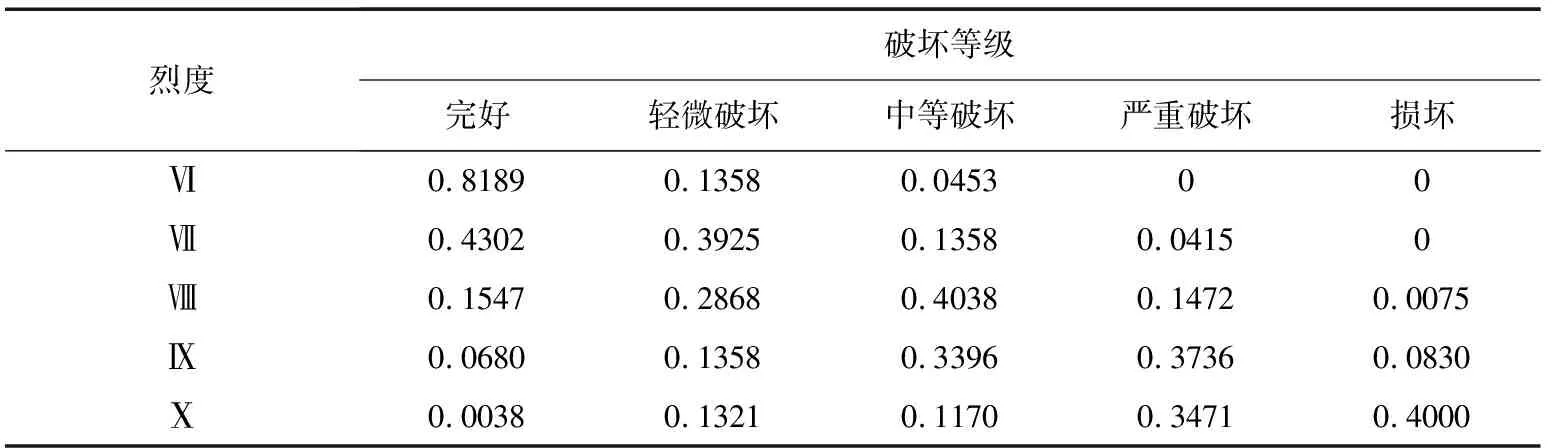
表2 某城市多层砌体房屋震害矩阵Table 2 Earthquake damage matrix of a multistory masonry building in a city

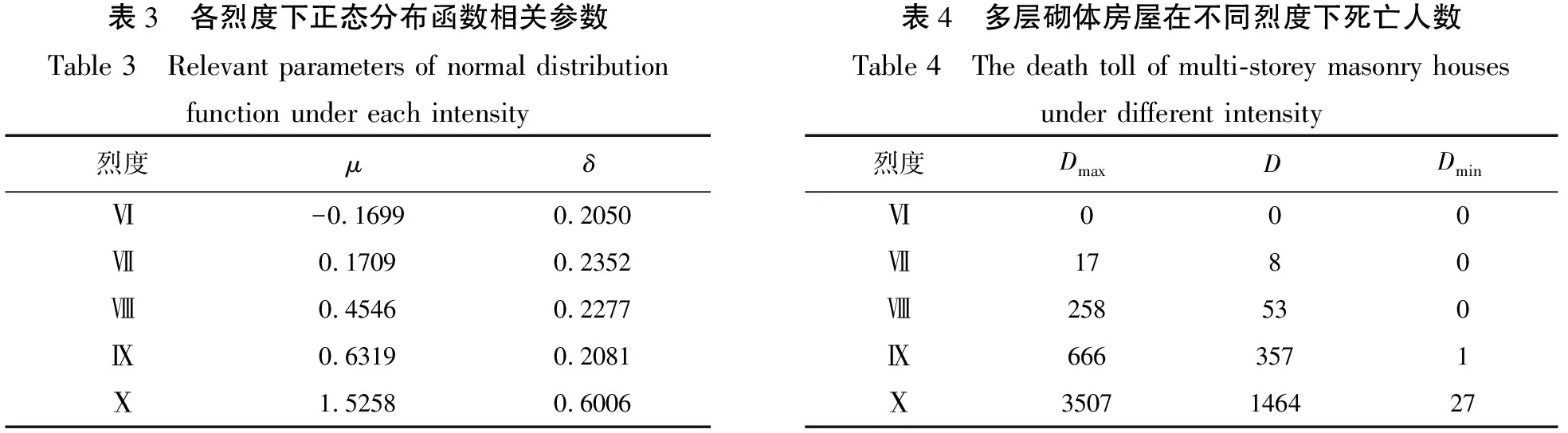
表3 各烈度下正态分布函数相关参数 Table 3 Relevant parameters of normal distribution function under each intensity烈度μδⅥ-0.16990.2050Ⅶ0.17090.2352Ⅷ0.45460.2277Ⅸ0.63190.2081Ⅹ1.52580.6006表4 多层砌体房屋在不同烈度下死亡人数Table 4 The death toll of multi-storey masonry houses under different intensity烈度DmaxDDminⅥ000Ⅶ1780Ⅷ258530Ⅸ6663571Ⅹ3507146427

1)将建筑物破坏等级按照震害指数进行数值化，以破坏等级对应的震害指数为横坐标，对应的概率为纵坐标，进行正态分布拟合，给出在各烈度下的正态分布函数N(μ,δ2)，具体参数见表3。

2)按照式(1)，可计算得到各烈度下各破坏等级比例约束上限。并根据各破坏等级比例约束上限，按照前文所述伤亡人数最值各破坏等级比例取值方法及伤亡人数计算方式，即可计算出各烈度下人员伤亡数最大值Dmax和最小值Dmin。同时为便于对比分析，采用传统基于建筑结构易损性的伤亡人数评估方法计算出基于建筑物易损性的死亡人数期望值D。见表4。

3)依据公式(2)、(3)计算出该城市多层砌体房屋在不同烈度下的对数死亡人数变化函数，如下表5及图2所示，其中表5中“-”表示在该烈度下无人员死亡，故无对数死亡人数函数曲线；图2中圆点的标注信息为采用传统评估方法得到的死亡人数期望值D在该函数曲线上的对数值及超越概率。

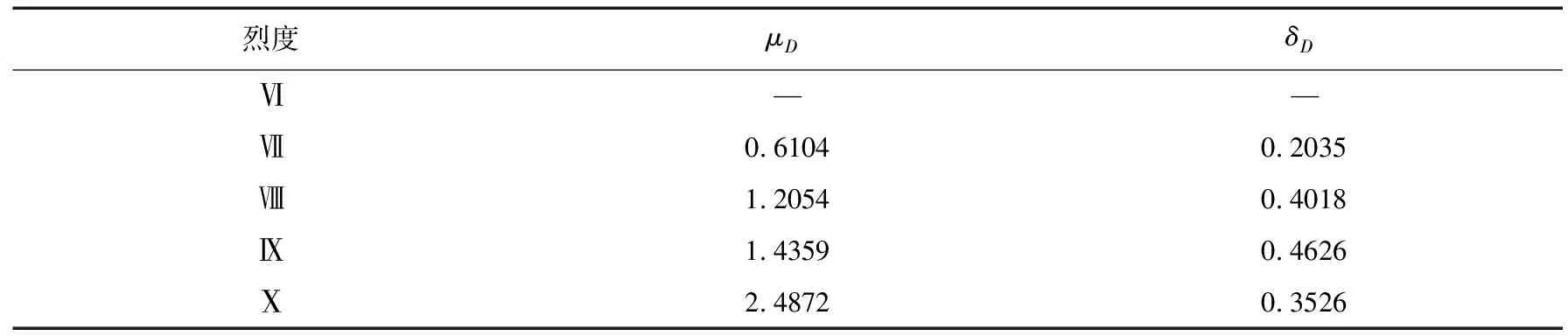
表5 多层砌体房屋在不同烈度下对数死亡人数函数相关参数Table 5 Relevant parameters of logarithmic death toll function for multi-storey masonry buildings under different intensities

地震造成的人员伤亡具有很大的不确定性，传统的期望值评估结果并不能反映预测结果的不确定性，无法给出某个数量级、某个范围内或超过某个关心阈值的可能性有多大。而不确定性分布函数曲线评估结果则可以根据曲线在某个范围的积分给出相应的概率数值表达。

分析算例评估结果：

(1)可以给出地震造成死亡人数基于超越概率的表达。某一死亡人数的超越概率即为超过此死亡人数的部分函数曲线与横坐标轴x=0所包围的面积。如图2(c)中多层砌体房屋在Ⅸ度下死亡人数达到357人的超越概率为0.0079。

(2)可以给出所关注的阈值区间的概率，即为两个死亡人数阈值区间的部分函数曲线与横坐标轴x=0所包围的面积。如图2(d)中多层砌体房屋在Ⅹ度下死亡人数在100人和1000人之间的概率为0.8436。

(3)人员伤亡是结构易损性的体现。本文方法是基于结构易损性结果给出的，能很好的反映地震作用强度及结构易损性的变化对评估结果的影响。

(4)传统的期望值评估结果，也不一定落在发生概率较高的范围内，而是随地震作用强度、易损性结果变化而变化的。初步分析是由于伤亡是易损性结果与不同烈度对应的死亡率相乘导致函数曲线的变化及对数转换所造成的。

(5)与现有的基于建筑结构易损性人员伤亡期望值评估方法对比可发现，本文方法能给出更多基于概率、超越概率的表达。由于实际房屋建筑的震害表现具有很强的不确定性，本文方法更能满足对震害损失的不确定性的描述评估。可进一步描述低数量级发生概率高与高数量级发生概率低的风险对比问题。

对拥有多种建筑结构类型的情况，可基于卷积公式，给出同一烈度下的联合人员伤亡概率密度函数。为便于实际应用，再选取多个人员伤亡阈值处的概率密度函数值，拟合给出对数正态分布函数。同理，给出具有不同烈度的整个评估区人员伤亡对数正态分布函数。

5 总结与展望

本文提出了基于切比雪夫不等式的人员伤亡评估模型，给出人员伤亡函数曲线，得到基于概率、超越概率表达的人员伤亡评估结果，反映了建筑物易损性对伤亡评估结果的影响。相对于基于建筑物易损性的期望值评估方法则更能充分描述评估结果的不确定性。并以算例分析验证了评估方法的适用性。

然而本文方法仍有不足之处，如函数均值和方差是基于经验方法给出的，有一定的主观性，对数正态分布虽是常用的损失表达方式，但忽略了易损性从截断正态分布到伤亡的对数正态分布的转变所造成的误差。为进一步提高人员伤亡评估模型的精确性，在今后的研究中将会用蒙特·卡洛方法对比验证经验方法，进而分析给出均值和方差的修正系数。