一种远距离局部极坐标约束在滚动轴承有限元求解上的应用研究
郭磊磊 奚卉 洪有财 陈小星 王凤才
(1.第七一五研究所,杭州,310023;2.青岛理工大学,青岛,266033)(3.西安交通大学,西安,710049)
长期以来国内的高精尖轴承的使用很大程度上都依赖从国外进口[1],关于滚动轴承的研究与西方发达国家相比仍处于相对落后状态,特别是轴承制造装配过程中的一些参数(轴与轴承内圈的过盈量、轴承内部游隙、轴承外圈与箱体的间隙等)一直沿用国外的标准,但对这些参数的机理并不清楚。
近年来发展的有限元在复杂结构求解方面具有很大的优势,但涉及轴承内部游隙以及间隙的问题,却鲜有文章利用有限元工具分析,其中一个重要的原因是在引入游隙和间隙后,在滚动体无附加约束时,容易产生刚体位移。文献[2]提出对滚动体施加切向约束的边界条件以消除刚体位移。该方法被很多学者借鉴学习并采用,但这却牺牲了求解的精度甚至正确性。文献[3]为消除刚体位移,对滚动体用弹簧单元约束,某种程度上消除了刚体位移,用接地软弹簧来约束滚动体,与系统刚度相比弹簧刚度应该小到可以被忽略,以确保对求解不会产生影响。但弹簧刚度取值大小需反复的实验,对于复杂问题求解仍然有很大的困难。另外还有一些学者提出动力学求解[4-5],惯性作用可以阻止刚体运动,即克服刚体运动的一种选择是动态求解。这需要加上质量和阻尼使求解从静态转化为动态,但要缓冲掉不想要的动态影响很不容易,另外这种方法求解效率也比较低。还有一些学者提出在恰好碰上的位置上建立几何模型[6-7],但对于位置不确定或表面是曲面及不规则的面,这样求解仍然很难进行下去;另外,由于有限元网格修整,仍不可避免存在间隙和小侵入,求解同样难以进行下去[8]。
本文基于有限元方法,利用远距离局部坐标对目标物体进行约束,通过增加远距离局部坐标与目标物体的距离,提高求解精度。
1 远距离极坐标约束方法
如图1 所示,R为球体或圆柱体半径,λ为球体或圆柱体与接触平台的间隙,D为球心O1距局部坐标系原点O的距离,α为N1O连线与极坐标轴X的夹角,β为N2的连线与极坐标轴X的夹角,F为施加到球体上的外力。边界条件:(1)将整个球体(或球体上任意两点)周向约束于局部极坐标系,则α和β值将保持不变(即切向约束);(2)将平台两端施加全约束;(3)球体上施加如图1 所示的力F。

图1 极坐标约束示意图
通过改变距离D(可以通过改变局部坐标系的位置),则接触平台的法向接触的合力F1将逐渐变大,最终与F趋于相同,而球体和平面的接触力也逐渐与理论解相同。当λ发生变化时,极坐标约束球体(被约束目标物体)上的角度坐标保持不变。根据几何关系,内部节点之间的相对距离必然发生变化,从而在内部刚度矩阵K的作用下,产生一定的内应力,从而反抗λ的变化,实现在静态计算中被约束目标软着陆,达到求解的目的。内应力不是物理真实存在的,而是由于该计算方法所带来的附加影响,但通过增大极坐标与目标物体之间的距离D,能够降低内应力的影响,最终将求解精度控制在一定的误差范围内。根据圣维南原理,极坐标在接触平台两端产生的内应力对接触区域的影响将会很小,这样可提高求解精度。
2 轴承滚动体的约束
如图2 所示,轴承滚动体约束分为滚动体无约束和有约束两种情况。前者分为轴承内部有游隙和无游隙两种情况。滚动体有约束(全局坐标周向约束),无论有游隙还是无游隙,均容易产生刚性位移,一般求解均不能收敛。因此按照周向约束(切向约束)以及远距离局部极坐标约束来分类。本文讨论全局坐标周向约束和远距离局部坐标两种方法。

图2 轴承滚动体约束分类
2.1 全局坐标周向约束
全局坐标周向约束为利用圆柱极坐标将轴承内部滚动体约束至轴承的几何中心上(即圆柱坐标下,约束滚动体节点的极角,在圆柱坐标下可设为UY,下同),只允许滚动体在径向发生弹性变形,以防止滚动体在静力学分析中产生刚体位移。但这种约束方法本身存在一定的缺陷,因为外力作用于外圈时,外圈将力传递到滚动体上。而滚动体在力的作用下,其内部节点将沿全局坐标系原点和它们原位置的连线运动,这样各节点上的力很大程度上因UY的约束而消耗掉,这与滚动体真实的结果会有很大不同。根据图3 可知,由于轴承的变形前后的长度OO′远小于轴承的几何尺寸,因此sinθ较小,故滚动体与内圈接触力在法向的分力应接近于滚动体与外圈接触力,即Qeq=Qiq,见图4。但经有限元计算发现,滚动体与内圈接触力小于外圈与滚动体约束力,如图5 所示。这与实际情况明显不符。

图3 单个轴承受力分析图
图4 轴承单个滚动体受力示意图
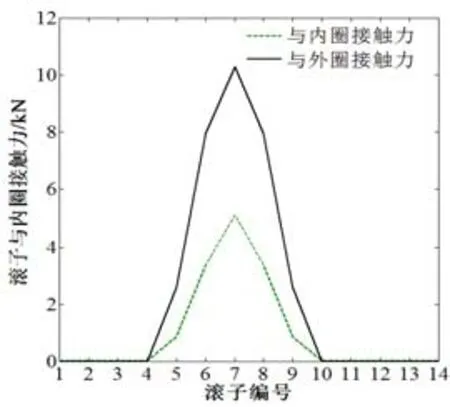
图5 单个轴承外圈及内圈与滚动体接触力对比
2.2 远距离极坐标约束
在图6 中,NJP3226 轴承的每个滚动体都建立了一个局部极坐标系,坐标系位置为沿滚动体中心到坐标原点的射线上,其中各个滚动体与其对应的局部极坐标系的距离为L。局部极坐标为圆柱坐标系,共有X、Y、Z 三个坐标。其中X坐标表示径向距离ρ,Y坐标表示方位角θ,Z与直角坐标系等值。NJP3226 轴承共14 个滚动体,因此建立14 个局部极坐标系,并将滚动体上节点的方位角θ约束在对应的极坐标系上。其他的边界条件参考第3 节有限元分析。

图6 局部坐标系建立示意图
3 有限元分析
3.1 滚动轴承有限元模型
以NJP3226 轴承为求解对象[9],该圆柱滚动体轴承的结构参数见表1。

表1 NJP3226 轴承尺寸参数
图7 为有限元模型,各实体均采用solid185 单元,轴承材料采用GCr15,额定工作载荷为30 kN,弹性模量为200 GPa,泊松比为0.3。边界条件:

图7 轴承有限元网格划分模型
(1)内圈内表面全约束;
(2)将滚动体分别采用不同的约束方法分析;
(3)将额定载荷等效为Fr=24 kN 分布于外圈外表面的余弦载荷(分布范围为:-82.8°≤θ≤ 82.8°)。载荷分布见图8。
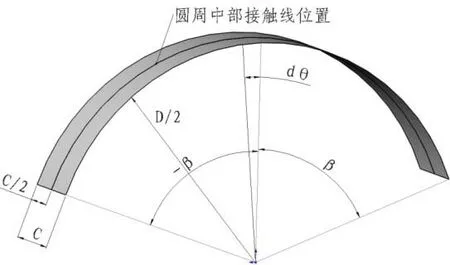
图8 载荷分布所在曲面视图
设余弦分布载荷为

其中,D=250 mm,C=80 mm,β=82.8°。代入方程解得A=1.68。则施加的余弦分布载荷为

3.2 结果分析
多体部件发生面对面接触时,以滚动体为接触面,内外圈滚道表面为目标面。各接触对中,设置摩擦因数为0.2,法向接触刚度因子为0.7,接触公式使用罚函数。计算结果如图9 所示。由图可知,当局部坐标系原点在滚动体中心时,内圈没有接触力作用;而当局部坐标原点距离逐渐远离整体坐标系中心时,内圈所受接触力逐渐增大,最后该应力趋近于确定值。同时外圈与滚动体的接触力不随局部坐标系距离的远近而变化。这是由于外力直接作用于外圈,而外圈并没有受到约束干扰,因此其受到的接触力不会因为局部坐标距几何中心距离的变化而变化。因此合理调节局部坐标距滚动体中心的距离能够提高求解精度,并能够保证求解的收敛性。
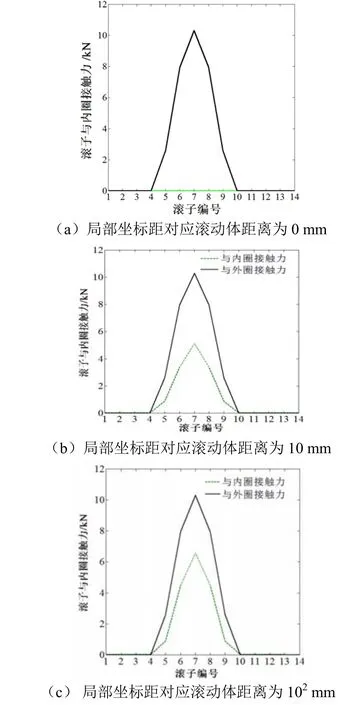
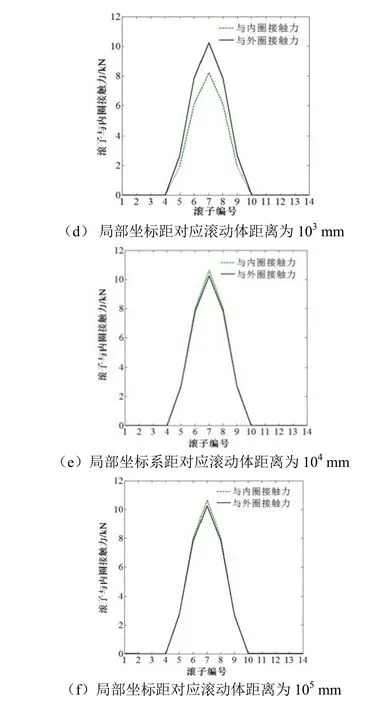
图9 滚动体与内外圈接触力随距离的变化
4 理论验证



图10 滚动体与内圈接触力的有限元解和理论解对比
5 结论
(1)对NJP3226 轴承内部滚动体进行切向约束时,只允许其在径向发生弹性变形,可以防止滚动体在静力分析中产生刚性位移。但经有限元计算发现,滚动体与内圈接触力<外圈与滚动体约束力,这与实际情况明显不符。
(2)采用远距离极坐标求解,随着局部坐标系距对应滚动体距离的增大,内圈与滚动体接触力逐渐趋近外圈与滚动体接触力。当局部坐标系与对应滚动体距离增大到一定程度后,内圈与滚动体接触力逐渐逼近外圈与滚动体的约束。
(3)采用远距离极坐标约束经计算后与理论结果较好的保持了一致,同时该方法不但能够满足求解精度,也提高了求解效率。
本文方法解决了轴承内部滚动体不受约束难以收敛的问题,同时也保证了求解精度,在工程应用上具有一定的推广意义。远距离局部坐标约束方法具有一定的普适性,其中蕴含的机理需要相关学者进一步研究。

