一种适用于φ-OTDR 系统的光纤振动信号快速模式识别算法
严爱博 宛立君 吴梦实
(第七一五研究所,杭州,310023)
近年来,φ-OTDR 已在长距离的周界安防[1,2]、管道预警[3,4]、船舶管道泄漏[5]、铁路安全监测[6]等领域中得到了高度的重视和广泛的应用。光纤振动信号是一种典型的非线性非平稳信号,加之光纤布局复杂,室外风雨等自然环境干扰,这些都导致了光纤信号特征提取和识别的精准度、稳定性难度增加[7-9]。
目前光纤振动信号识别可分为基于统计学的光纤振动信号识别算法和基于机器学习/深度学习的光纤振动信号识别算法。前者提取光纤信号在时域、频域及时频域中的某一个或某几个特征参数(如短时平均能量等),结合统计学方法进行入侵信号的检测和识别。S Mahmoud[10]、H Zhu[11]、卢娜[12]等先后提出基于时域包络特征、过阈值率、短时能量和短时过阈值的光纤信号识别算法,实现初步的干扰和入侵行为分类。此类算法的实现依赖于手动的特征提取,步骤较为复杂,且易受外界环境干扰,不适用于复杂环境下的光纤信号识别。
基于机器学习/深度学习的光纤振动信号识别算法首先利用一定的样本训练来学习入侵信号与入侵行为间的特征关系,找到最优的分类器或网络结构;再用训练好的识别模型对新的入侵信号进行识别。C Xu 等提出了基于谱减法-支持向量机( Support Vector Machines, SVM )[13]、基于卷积神经网络[14]的入侵信号检测,实现了93.8%的识别率。2019 年,Y Wang 等结合小波能量谱分析和相关矢量机,对三个干扰事件进行检测,识别率超过88.6%,但对其中的撞击和行人干扰难以区分,准确率略低于85%[15]。同年,H Jia 等提出了基于近类别支持向量机的事件识别算法,利用k 近邻算法将现有的二分类SVM 扩展到多分类问题中,在5 种扰动事件的识别分类中实现了94%的准确率[16-17]。相较于基于统计学的算法研究,此类算法在大样本训练的情况下受环境干扰小,在一定程度上降低了误报、漏报的可能性。
光纤振动信号识别的核心问题之一在于如何在复杂监测环境中实现小样本下对入侵信号的快速响应。本文提出LMD 和ELM 的光纤传感周界安防信号识别算法(LMD-ELM),实现了对入侵行为的报警和非入侵行为的识别,模型架构如图1 所示。
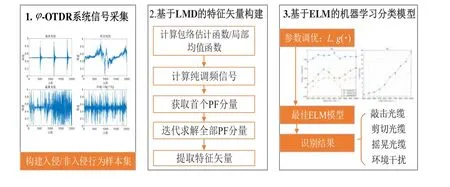
图1 基于LMD-ELM 的模型架构
1 相位敏感光时域反射系统
φ-OTDR 系统是一种典型的分布式光纤传感系统,其基于瑞利散射原理,并结合光时域反射技术,可实现振动位置的准确定位。本文采用基于相干探测的φ-OTDR 系统结构,如图2 所示。系统采用相干探测结构将返回的后向瑞利散射光与光源激光器发出的本振光在2×2 光纤耦合器中进行干涉,之后利用光平衡探测器完成光电探测,去直流并保留振动信号的交流分量。最后,经过振动信号解调算法,实现弱信号的远距离测量,获取振动发生的位置信息以及振动信号的相位、频率、幅度等特征信息。在某一时刻,光电探测器接收到的电信号为:
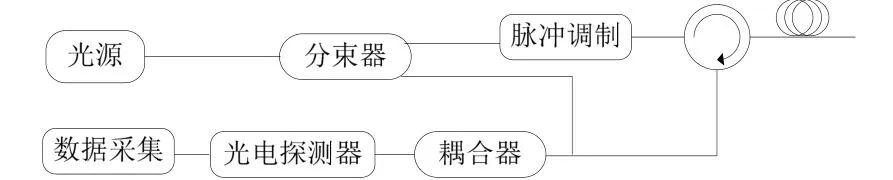
图2 相位敏感光时域反射系统结构图

式中,A是反射强度系数,w是声光调制器引入的信号载波频率,y(t)是解调之后传感光纤特定位置某时刻的相位信息,即后文用于入侵事件识别的输入信号。
2 方法
2.1 基于LMD 的特征矢量构建
LMD 自适应地将一个复杂的非平稳的多分量信号分解为若干个瞬时频率具有物理意义的乘积函数(Product Function,PF)之和,其中每一个PF分量由一个包络信号和一个纯调频信号直接求出。将计算得到的PF 分量作为ELM 的输入矩阵,为光纤振动信号的识别提供充分的特征信息。对于任意的光纤振动信号y(t),其完整的输入矩阵构建如图1中的第2 部分所示。针对传统经验模态分解在信号分解中存在的端点效应和模态混叠现象,本文提出利用LMD 进行信号分解,步骤见下文。
2.1.1 计算包络估计函数A和局部均值函数B

2.1.2 计算纯调频信号S1
首先依据式(4)计算s11;其次若满足式(5),则s11为纯调频信号,若s11不是纯调频信号,则将其作为原始光纤振动信号重复式(2)~(4)的计算, 直到s1m为纯调频信号, 从而得到

2.1.3 获取首个PF 分量
依据式(7)求解得到第一个PF 分量,同时根据式(8)计算余量U1。
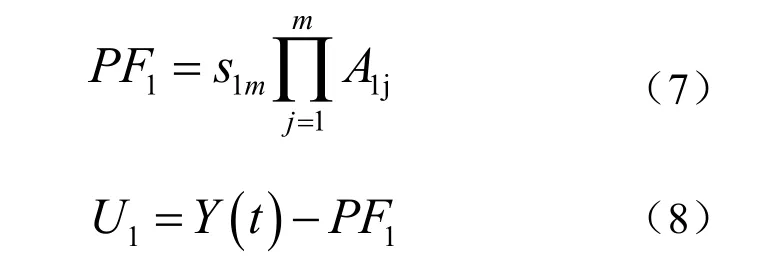
2.1.4 迭代求解全部PF 分量
将余量U1作为原始光纤振动信号循环(2.1.1)~(2.1.3)的步骤,得到PF2,…,PFk,直到余量Uk为单调函数。


图3 敲击光缆振动信号LMD 分解示意
2.1.5 提取特征矢量

2.2 基于ELM 的机器学习分类模型
作为一种特殊的前馈神经网络( single hidden layer feed forward network, SLFN),ELM 通过随机选取输入层权重和隐藏层偏置获取相应的输出权重,相较于传统的SLFN 实现了更快的模型训练,且具有模型参数少、泛化性能强等优势,已成功应用于计算机视觉、图像处理、时间序列分析等领域[17]。ELM 网络采用最小二乘法进行优化,无迭代过程。
ELM 的基本结构如图4 所示,概括其神经网络的训练步骤可分为随机特征映射和线性参数求解两个阶段。详细的算法求解如表1 所示。

图4 ELM 模型的基本结构
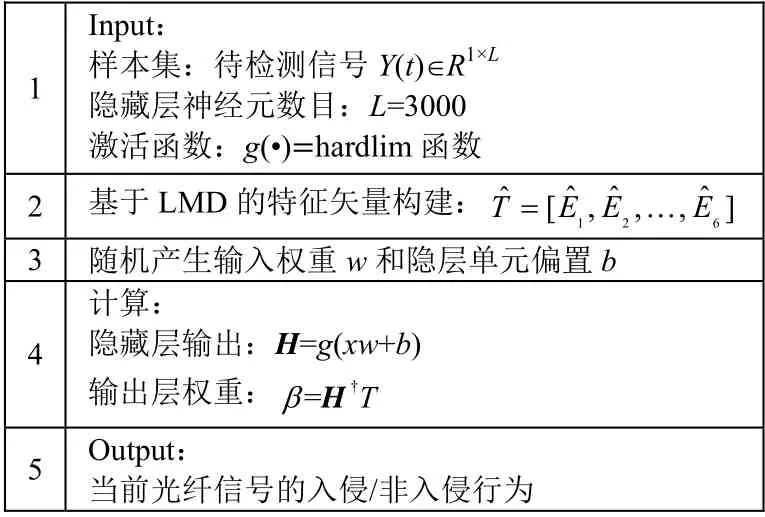
表1 基于ELM 的分类模型算法
对其中的重要参数做如下说明:g(•)是隐层节点的激活函数,与隐藏层神经元共同决定ELM 模型的非线性逼近能力,直接影响模型的算法性能。此外,输入权重w以及隐层单元偏置b在训练过程中随机初始化;输出权重β的计算公式中,H†为隐藏层输出矩阵H的Moore–Penrose 广义逆矩阵,T为期望输出。
3 实验结果与分析
3.1 实验数据
为验证算法的有效性,本文采用如图2 所示的φ-OTDR 系统,并且以挂网方式将光纤传感光缆布设于围栏上进行现场数据采集,其中采样频率为100 kHz。对φ-OTDR 系统的传感光缆施加入侵行为,包括敲击光缆、剪切光缆、摇晃光缆,以及环境干扰事件(大雨天气中采集),同时从数据采集中心获取入侵及干扰时的光纤振动信号。本文采集了4 种入侵/干扰行为的光纤信号各100 组,每个信号长度为2000(便于数据处理及运算,将采样率从100 kHz 降采样至2 kHz),典型的4 种入侵/非入侵原始光纤信号如图5 所示。
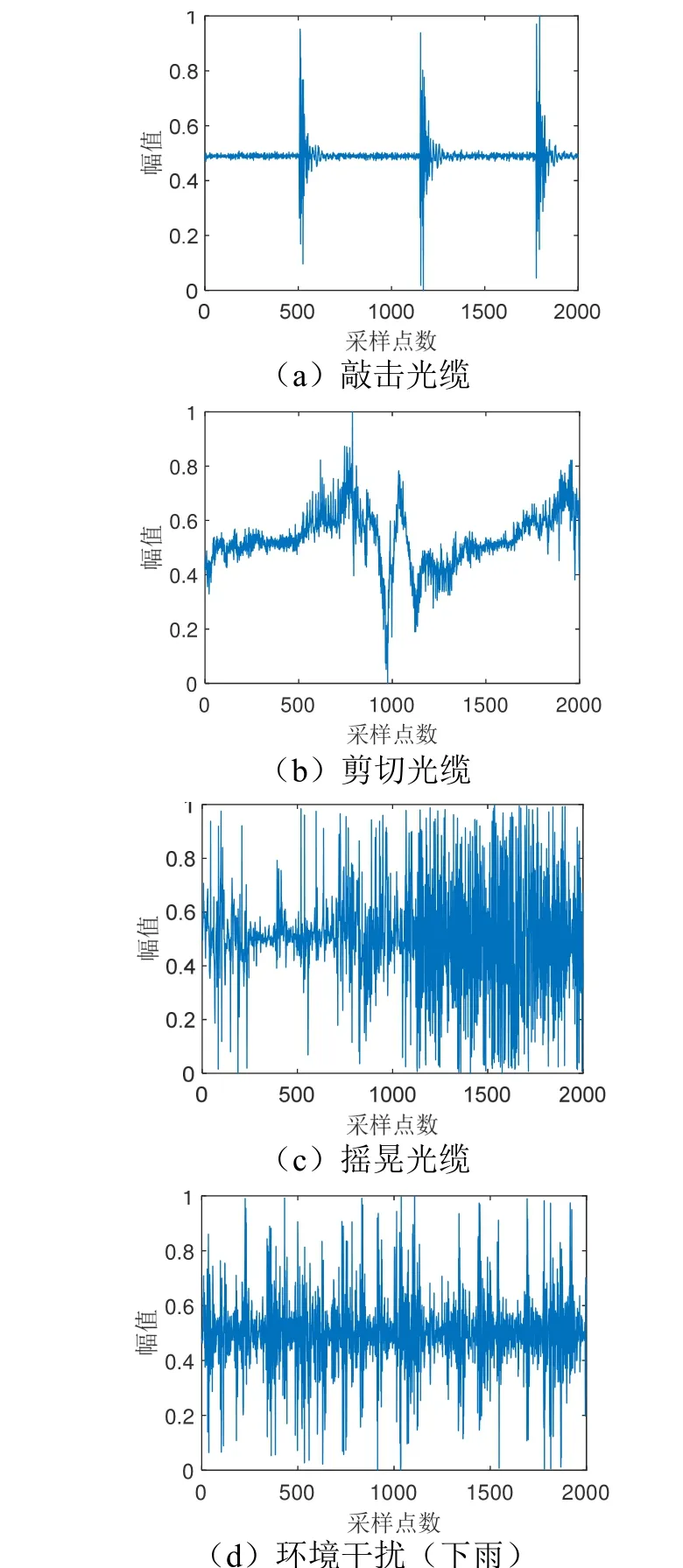
图5 φ-OTDR 系统现场采集的原始信号
3.2 模型参数优化
考虑到隐藏层神经元数目L和激活函数g(•)直接关系到ELM 分类模型的性能,本文以4 个经典的分类指标来进行模型参数的优化和确定,分别为准确率(accuracy, Acc)、灵敏度(Sensitivity, Se)、特异性(Specificity, Sp)、识别时间(Test time, T)。在实验中,设定隐藏层神经元数目L∊[1000,10 000],其中以步长1000 逐步增加,综合比较了hardlim 函数、sigmoid 函数及sinusoid 函数这3 个常用的激活函数的识别性能,如图6 所示。
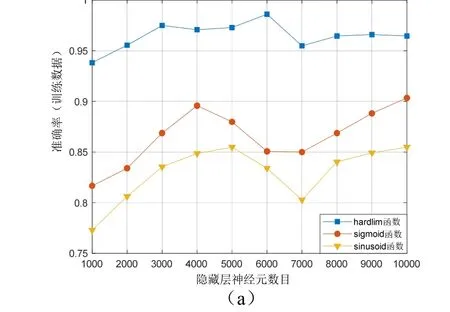
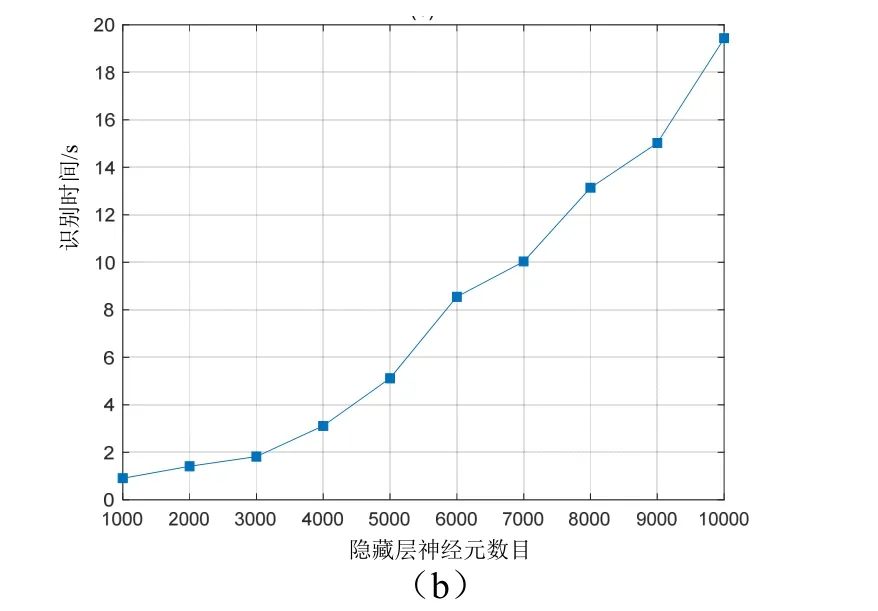
图6 不同激活函数/隐藏层神经元数目下的性能
分析图6(a),其中hardlim 函数的识别率明显优于其他两个激活函数,且受隐藏层神经元数目的影响较小。图6(b)给出了hardlim 函数在不同隐藏层神经元数目下的识别时间。权衡考虑识别精度和测试时间,本文选取L=3000,此时的LMD-ELM 模型可在满足97.50%的较高识别性能下实现快速的警报响应。
3.3 结果与讨论
我们实验比较了3 种不同的方案在3 个分类指标上的性能,数据见表2。方案2 虽然实现了较好的精度,但其每一入侵/非入侵行为的响应时间(即识别时间)相对于方案1 和方案3 表现较差。究其原因,一定程度上源于ELM 避免了梯度式的学习和迭代过程。相较于方案2 和3,本文方法不仅在准确率、特异性等指标上取得了理想的识别结果,而且在一定程度上缩减了模型的训练和分类时间,总体性能较好。

表2 不同方案的训练和测试效果
4 结论
为缩短现有的光纤传感周界安防信号识别算法在φ-OTDR 系统应用中的响应时间,实现对入侵行为的精准响应,本文提出了基于局部特征分解和极限学习机的识别算法。采集现场的4 种入侵/干扰光纤振动信号,结合4 个经典的性能指标综合分析方法的分类性能。实验数据表明,本文算法能有效区分敲击、摇晃、攀爬等3 种入侵行为和风雨环境这一干扰行为,实现了总训练识别性能97.50%、总测试识别性能95.00%、平均响应时间2 s 的稳定有效识别。此外,ELM 算法在训练过程中的计算复杂度也得到了有效控制,有利于φ-OTDR 系统在不同应用环境下的实时性要求。

