地震作用下起重机对高桩码头的动力响应影响
张安琪,苏 雷,凌贤长,,唐 亮,解立波,周林禄
(1. 青岛理工大学土木工程学院,山东,青岛 266033;2. 哈尔滨工业大学土木工程学院,黑龙江,哈尔滨 150090)
随着全球对进出口贸易的需求越来越大,港口建设的发展随之加快。为保证供需平衡,港口吞吐量日益增加,对集装箱起重机性能的要求也越来越高。我国沿海港口群处于活跃的环太平洋地震带,特别是环渤海地区和东南沿海地区港口群受郯庐断裂地震带、华北地震带和东南沿海地震带影响非常显著。起重机−码头结构体系势必会受地震带活动的影响,因此需要对其抗震性能进行重点考虑。特别是近年来地震活动进入新的活跃期,使起重机-码头结构体系抗震设防成为当前港工防震减灾的关键。如1995年阪神地震中,港口码头设施遭到严重损害,部分起重设备几乎瘫痪,不仅在经济上造成很大的损失,也为震后救灾物资的输送带来不利影响。自此人们开始认识到,港口对一个国家而言不仅仅是经济枢纽,还能在重大灾害发生时提供物资和救援上的保障。高桩码头作为港口最常用的结构形式,其动力特性一直是国内外学者关注的焦点。国内外学者对于高桩码头的特性分析进行了大量研究。如Zhang等[1]通过数值分析,比较分析了全直桩高桩码头与传统高桩码头动力响应的差异性。Chiaramonte等[2]通过有限元法和理论分析相结合的方法,分析了全直桩高桩码头的动力响应和失效模式。王元战等[3]依据结构安全分级标准规范,建立了高桩码头的安全度定量分级方法。陶桂兰等[4]考虑桩顶纵向变位对高桩码头的影响,并假定上部结构为刚体,推导出全直桩码头的水平荷载分配公式。王浩天等[5]基于p-y曲线法,对全结构段和单排架的梁板式高桩码头模型进行了对比,着重分析其桩基内力响应。江义等[6]总结了高桩码头在强震作用下的失效破坏模式,并结合工程实例,认为规范FEMA-440推荐的系数调整法可用于高桩码头的地震位移评估。廖雄华等[7]针对高桩码头-岸坡土体相互作用体系,建立了平面应变模型,进行了数值分析。陈光明等[8]利用ANSYS,基于不同规范的反应谱分析方法,对高桩码头各构件内力进行了分析与比较。虞鑫等[9]针对高桩结构的不同桩基布置形式,利用有限元法对其进行了动力响应分析。
近年来,关于高桩码头的研究很多,但大多数把起重机简化为集中质量直接施加在码头结构上或者忽略起重机的存在,这样得出的结果与实际情况存在一定偏差[10−12]。Shafieezadeh等[13]研究认为:地震中码头结构上部起重机发挥与阻尼器类似的减震作用。因而在数值模型中,往往只包含小部分质量而忽略起重机−码头结构相互作用(Crane-Wharf Interaction)。然而,精细数值模拟发现,起重机不仅不能减轻码头结构的反应,反而对其进行了放大。因此,在高桩码头地震反应评估中,需考虑起重机-码头结构相互作用。Long Beach港口码头设计规范指出[14]:当起重机移动方向周期小于2倍码头结构周期时,需考虑起重机-码头结构相互作用。为此,有学者针对起重机-码头结构相互作用进行了研究,旨在更加合理的确定高桩码头的动力响应。如Jaradat等[15]对起重机−码头整体结构进行了非线性时程分析,给出了起重机-码头结构相互作用的分析方法和模拟技术,并对起重机结构设计进行了修正,减小了码头的横向位移与轨道抗剪需求。Li等[16]建立三维有限元模型,研究了码头结构固有振动特性与起重机-码头结构固有振动特性的差异,并分析了不同地震动作用下码头结构的动力响应特性。Kourkoulis等[17]针对码头-土体-面板-起重机相互作用体系,进行了系统的非线性有限元数值模拟并实施了参数优化分析。结果表明:在水平地震动作用下,根据地面运动的特点,起重机可能会由于其海侧腿部的内力重分布而对面板产生额外的荷载,破坏面板稳定性,进而产生更大的破坏。宋波等[18]建立了起重机-码头结构的三维有限元数值模型,对地震作用下整个结构的反应特性进行研究,发现起重机明显地影响了高桩码头地震反应。可见,对高桩码头进行地震反应特性分析时,需考虑起重机−码头结构相互作用效应。
综上所述,目前对于高桩码头的特性研究大多数未考虑上部起重机结构的惯性作用,或将起重机结构简化为集中质量。考虑到起重机-码头结构相互作用的研究相对较少,对于起重机如何影响码头结构动力响应方面的工作还不够细致。鉴于此,本文针对典型起重机-码头结构相互作用体系,基于开源有限元数值计算平台OpenSees,建立三维起重机-码头结构相互作用数值模型。结合起重机模态分析结果,考虑上部起重机结构的惯性作用,重点关注地震作用下起重机对码头结构响应的影响。需要注意的是,本文所研究的高桩码头基于实际典型码头结构——加州洛杉矶港集装箱码头建立,地层情况基于该集装箱码头的实际土层勘察报告[19]。研究结果可为类似地层情况下码头结构体系的抗震设计与震害防控提供参考与借鉴。
1 起 重 机-码 头 结 构 相 互 作 用 三 维有限元模拟
1.1 起重机三维有限元模拟
本文所采用的大型起重机为近岸高桩码头常用的起重机,起重机总长133.5 m,前大梁长72.5 m,后大梁长30.5 m,总高度为67.3 m,结构总重1200 t,前大梁所处位置为海侧,后大梁所处位置为陆侧,如图1所示。起重机结构全部由Q235钢杆件组成,弹性模量为206 GPa,泊松比为0.3,材料密度为7830 kg/m3。在数值模拟中,起重机杆件采用弹性梁−柱单元模拟,杆件之间的连接假定为刚性连接,起重机的重量和质量通过单元节点施加,其建模方向规定为:起重机垂直于车轮轨道方向为x向,沿车轮轨道行走的方向为y向。需要说明的是,在本文中所涉及的数值模拟全部基于开源有限元数值计算平台OpenSees(http://open sees.berkeley.edu)[20]完成。
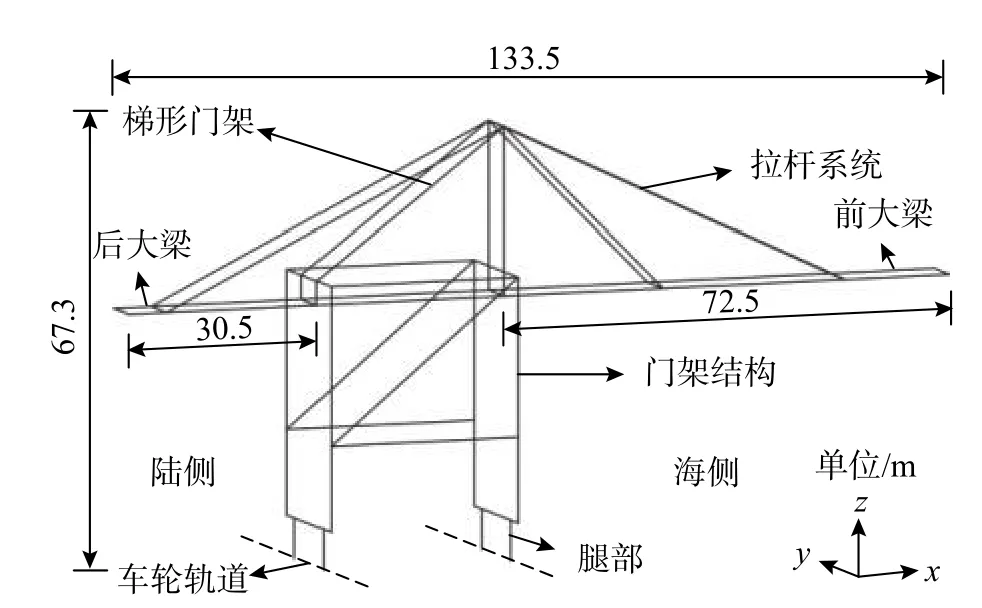
图 1 集装箱起重机结构Fig.1 Container crane structure
1.2 高桩码头体系数值模拟
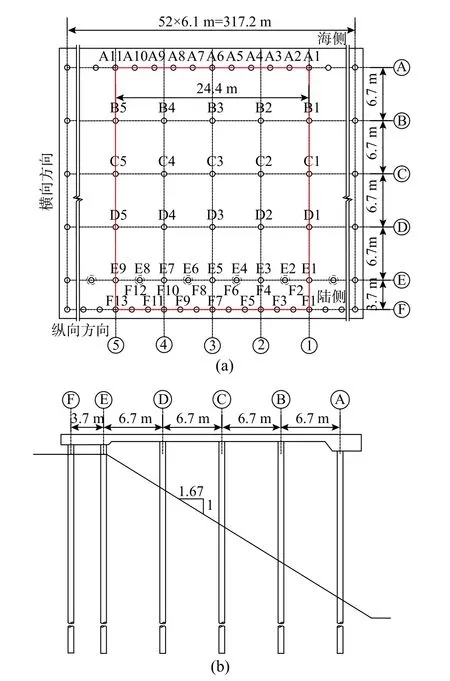
图 2 高桩码头结构体系布置Fig.2 Configuration of pile-supported wharf structure system
高桩码头结构体系布置见图2[21]。沿纵向,结构可视为由厚度6.1 m的相同条状组成,共52条,即沿纵向码头结构总长度为317.2 m。上部结构由6排预应力混凝土桩进行支撑,除F排与E排桩间距为3.7 m外,其余各排桩间距均为6.7 m。E排有短桩,桩长为17.8 m(图2中已圈出,即E2、E4、E6和E8),其余桩长均为42.0 m。考虑到所建起重机尺寸,下部码头结构选取四榀共48根桩(桩号已标出)进行模拟。如此,横向总长度为30.5 m,纵向总长度为24.4 m,如图2实线框所示。高桩码头结构体系所在土层分布见图3。土层的体积模量基于推荐的泊松比和剪切模量计算得到,其余参数基于实际码头结构所在地层的勘察报告获得,各土层的力学特性见表1[21]。在数值模拟中,高桩码头采用非线性Winkler地基梁模型(Beam on Nonlinear Winkler Foundation model)。在该模型中,预应力混凝土桩采用基于位移的非线性纤维梁-柱单元模拟,码头面板采用弹性梁-柱单元模拟,桩与面板的重量和质量通过单元节点施加,桩-土相互作用采用非线性弹簧单元模拟。
1.2.1 桩-土相互作用
在地震作用下,桩-土界面响应是一个非常复杂的动力相互作用问题[22−24]。在数值模拟中,为了更好的模拟桩-土动力相互作用,采用三类零长度弹簧单元,即p-y弹簧、t-z弹簧和Q-z弹簧,如图4所示。通过不同土层的特性参数(见表1),根据相关公式定义了不同的弹簧参数[25]。在数值模拟中,桩-土相互作用的具体模拟方法为:在土层中的每一桩节点处相同位置增设额外的两个节点,即节点1和节点2。桩节点与新增节点1之间使用equalDOF命令[26],保证桩节点与新增节点1之间拥有相同的平动位移。新增节点1和节点2采用代表桩-土相互作用的非线性零长度弹簧单元连接。其中,p-y与t-z弹簧分别模拟桩-土相互作用的水平向响应和侧向响应,Q-z弹簧模拟桩端处竖向桩-土相互作用。新增节点2采用完全固定约束。采用这三类弹簧单元可以模拟桩-土界面在地震作用下出现的摩擦、滑移和分离等情况。这三类弹簧所代表的曲线随着地震荷载的施加而动态变化,能够有效地模拟地震过程中桩-土动力相互作用[27],在桩基简化分析中得到广泛的应用[28−31]。以F排桩为代表,图5为F排桩在典型深度下p-y弹簧、t-z弹簧与Q-z弹簧受循环荷载下(如图5(a)所示)的力-位移响应示意图。三类非线性弹簧的力-位移响应随埋深和土层的不同而发生变化,在此不一一列出。
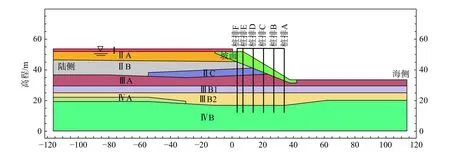
图 3 土层剖面分布(不同的颜色代表不同土层)Fig.3 Profile of soil layers (different colors represent different soil layers)
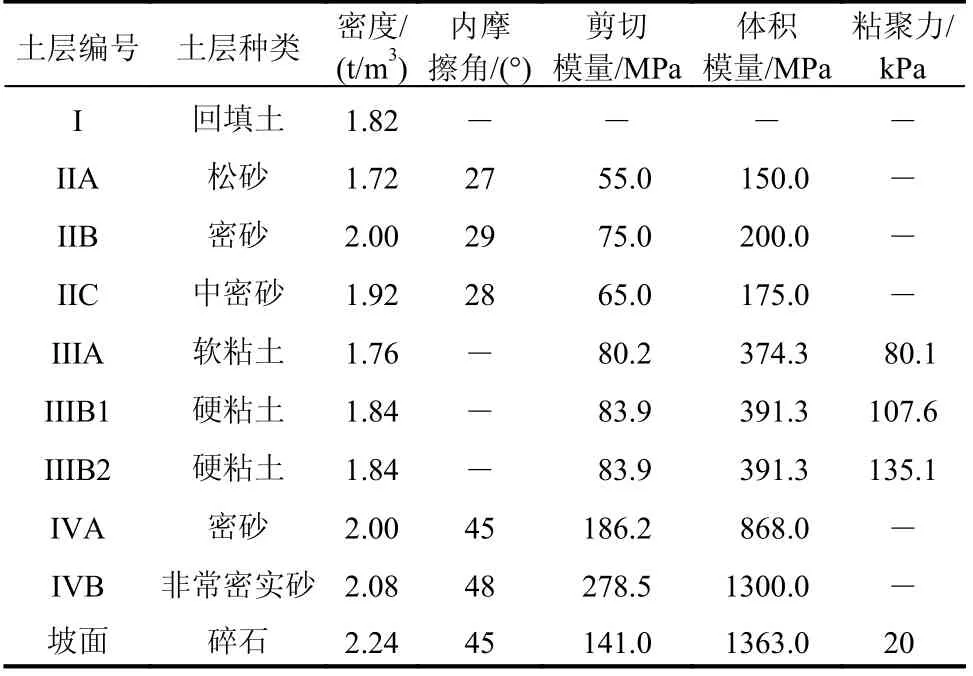
表 1 土层物理和力学特性Table 1 Physical and mechanical properties of soil layers
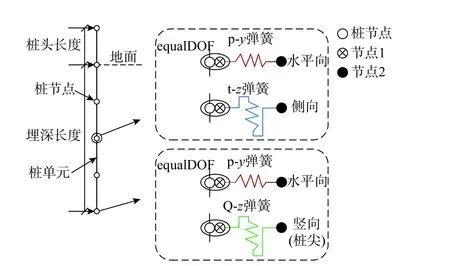
图 4 桩-土相互作用模拟Fig.4 Modeling of soil-pile interaction
1.2.2 预应力钢筋混凝土桩的模拟
桩身横截面是规则的正八边形,边长为253 mm,见图6(a)。将其离散成纤维截面,见图6(b),纤维截面钢筋采用Steel02材料进行模拟,约束和非约束混凝土采用Concrete01材料进行模拟[26],钢筋和混凝土材料参数见表2和表3。约束和非约束混凝土及钢筋材料在循环荷载(见图5(a))下的应力-应变响应特性见图6(c)~图6(e)。通过定义截面中钢筋、约束混凝土和非约束混凝土的材料性能,得到不同轴向荷载下桩截面的弯矩-曲率关系,见图6(f)。关于预应力钢筋混凝土桩的模拟详细细节见文献[32 − 33]。
1.3 起重机-码头结构数值模型
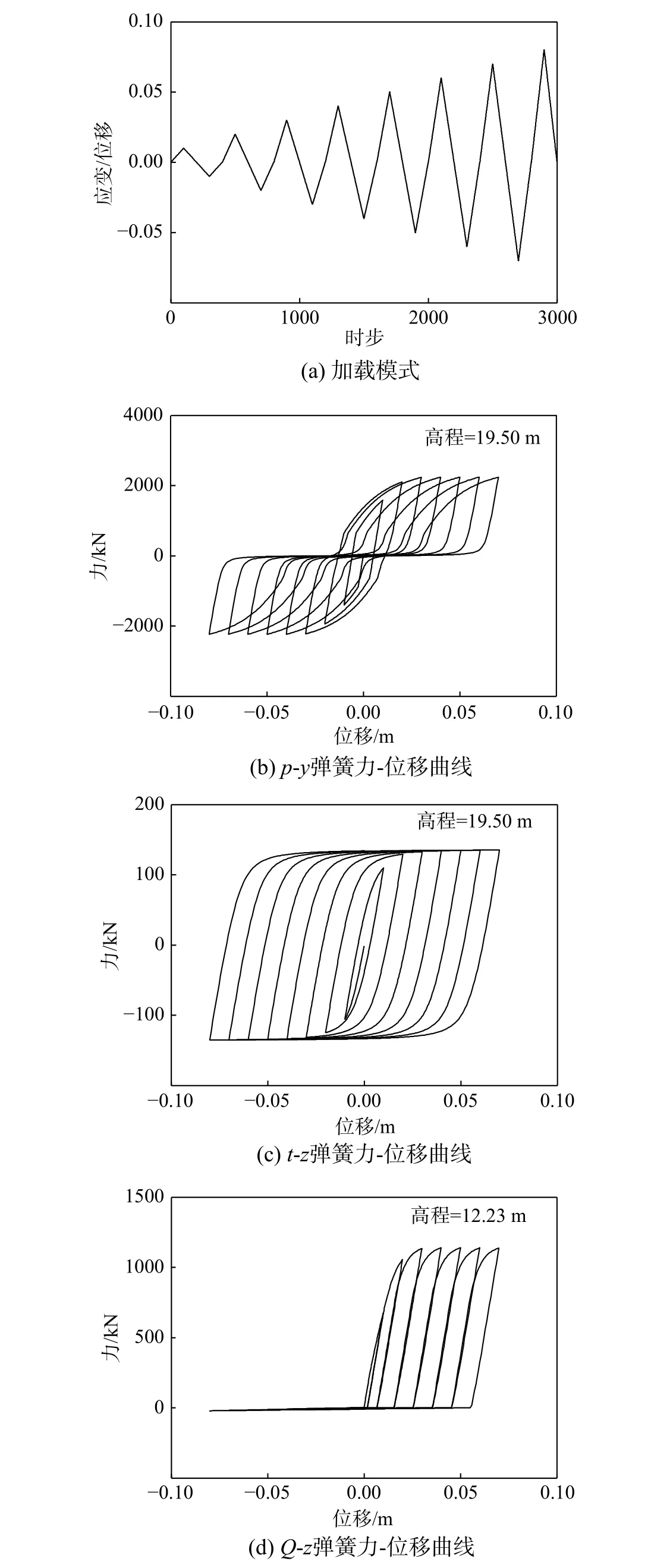
图 5 F排桩弹簧力−位移曲线Fig.5 Spring force-displacement response of pile row F
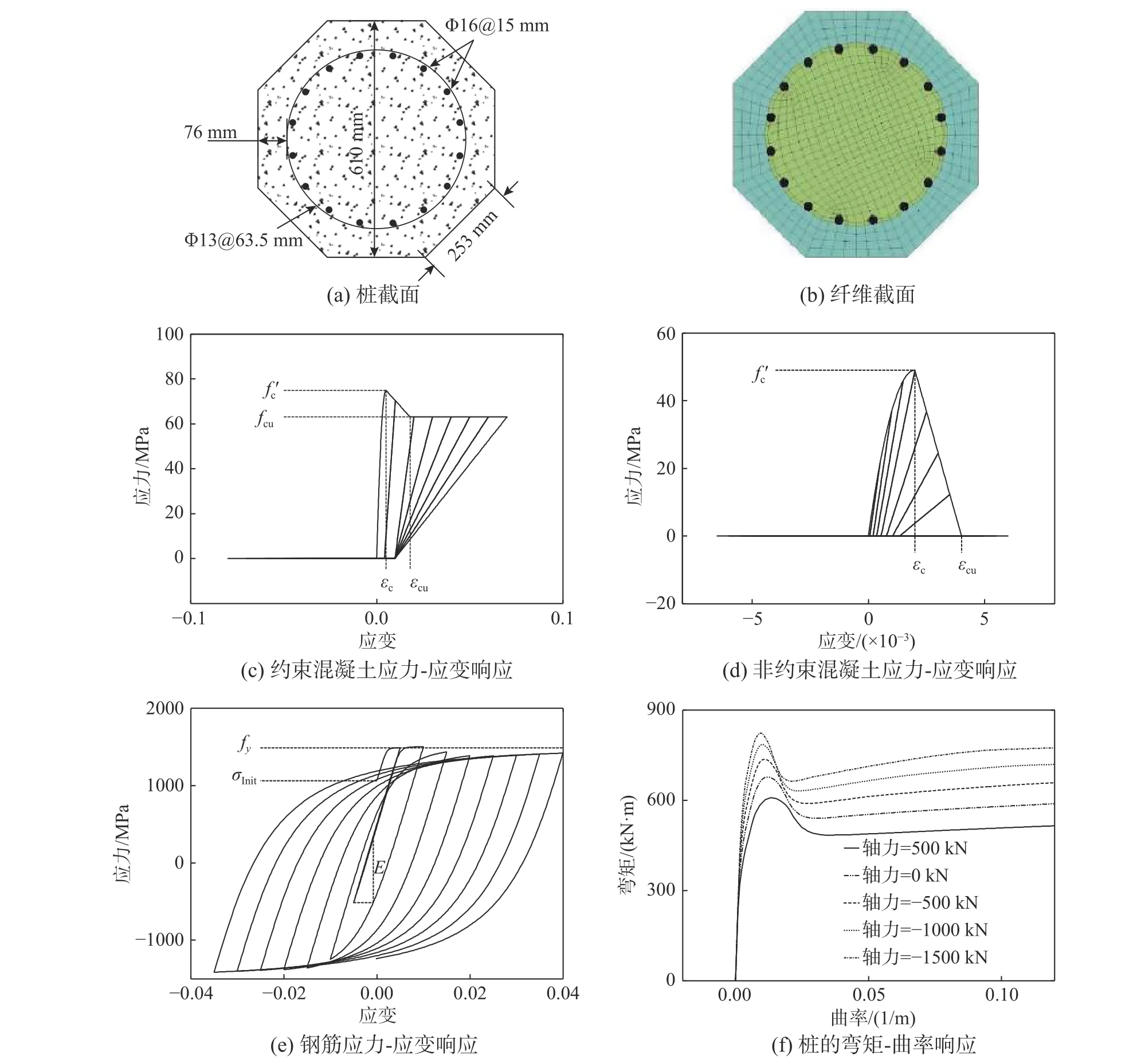
图 6 预应力钢筋混凝土桩的模拟Fig.6 Modeling of prestressed reinforced concrete pile
码头起重机的质量主要集中在前、后大梁上,集装箱起重机前大梁的状态,随实际工作状态的不同而改变。当前大梁处于伸直状态时,由于大梁长度与高度的影响,结构的振动幅度达到最大,对下部码头结构的影响最为明显。鉴于此,在分析起重机-码头结构相互作用时,设定起重机前大梁处于伸直状态,所建起重机-码头结构数值模型见图7。本文暂不考虑起重机整体脱轨对码头结构的影响,故起重机与码头下部结构的边界条件假定为刚性连接,用equalDOF命令,使其接触点拥有相同的平动位移和转动位移。当考虑起重机结构后,其重量通过其腿部与码头面板的接触节点传递到下部码头结构,此时各桩节点与面板节点所受荷载除自重外,还要承受起重机传递的荷载。起重机为非对称结构,因而传递到各接触节点的力各不相同。由于下部码头结构各桩的桩距、埋深不一样,导致其荷载的传递更加复杂。
1.4 地震波输入
为使模型在其地震作用下呈现明显的变形特性和非线性特性,模型基底地震动采用相对较高的峰值加速度[34]。考虑到该码头所处场地类型为D类场地,选取美国洛杉矶Northridge地震中Rinaldi Receiving台站记录的S48W分量地震动作为基底输入,该台站所处场地类型为D类场地。考虑到土层传播对地震动的影响,将记录的加速度幅值缩小一半作为输入地震动[21]。起重机结构的超长悬臂结构特性决定了在沿大梁方向(x方向)的地震动作用下,其对码头结构的动力响应影响最明显,将处理后的地震动(见图8)沿模型基底x方向输入[18,35]。
2 起重机对码头结构动力响应影响
2.1 起重机模态分析
为了更好的研究大型集装箱起重机对下部码头结构的影响,需先了解起重机自身的动力特性。对三维起重机模型进行自振特性分析,得到起重机不同阶模态响应如图9所示。一阶模态周期为2.51 s,振型主要特征为前大梁发生绕z轴的转动;二阶模态周期为1.90 s,振型主要特征为腿部与门架结构向海侧倾斜,前后大梁同时发生绕z轴的转动;三阶模态周期为1.18 s,振型主要特征为腿部与门架结构向陆侧倾斜,前后大梁绕z轴转动;四阶模态周期为0.93 s,振型主要特征为梯形门架和拉杆绕y轴发生侧移;五阶模态周期为0.80 s,振型主要特征为前后大梁大幅度上下摆动;六阶模态周期为0.55 s,振型主要特征为前、后大梁与梯形门架绕z轴前后摆动。以上起重机自振模态特性表明:在地震作用下,腿部与门架结构的左右摇摆及前后大梁的上下摆动都会对码头下部结构的内力造成一定程度的影响。
2.2 起重机对码头桩基地震响应的影响

表 2 钢筋材料参数Table 2 Material parameters for steel
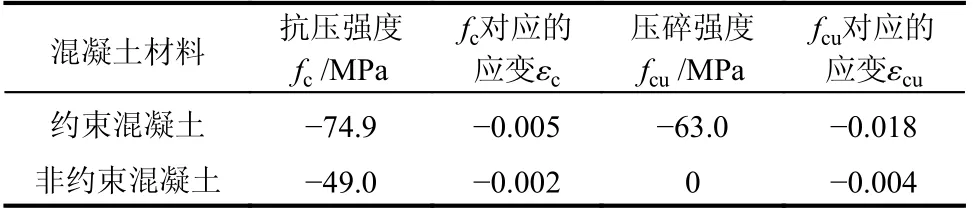
表 3 混凝土材料参数Table 3 Material parameters for concrete
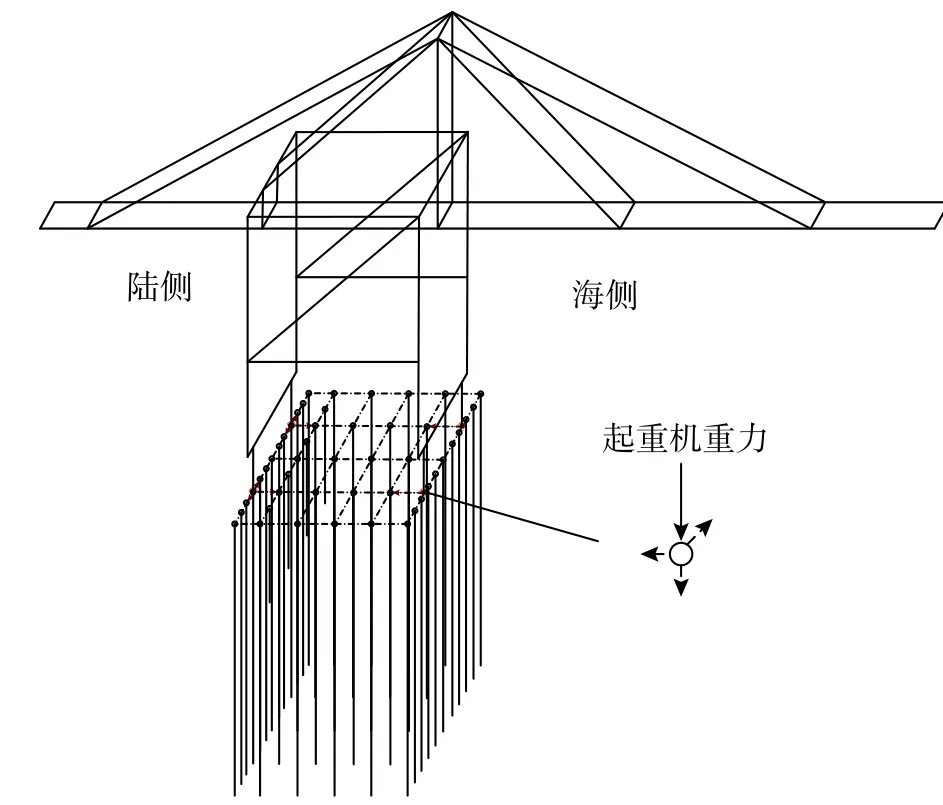
图 7 起重机-码头结构数值模型Fig.7 Numerical model of crane-wharf structure
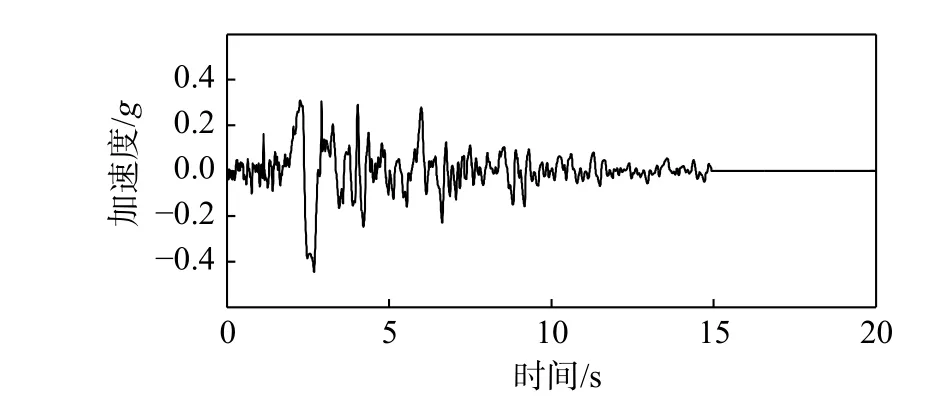
图 8 基底输入加速度时程Fig.8 Base input acceleration time history
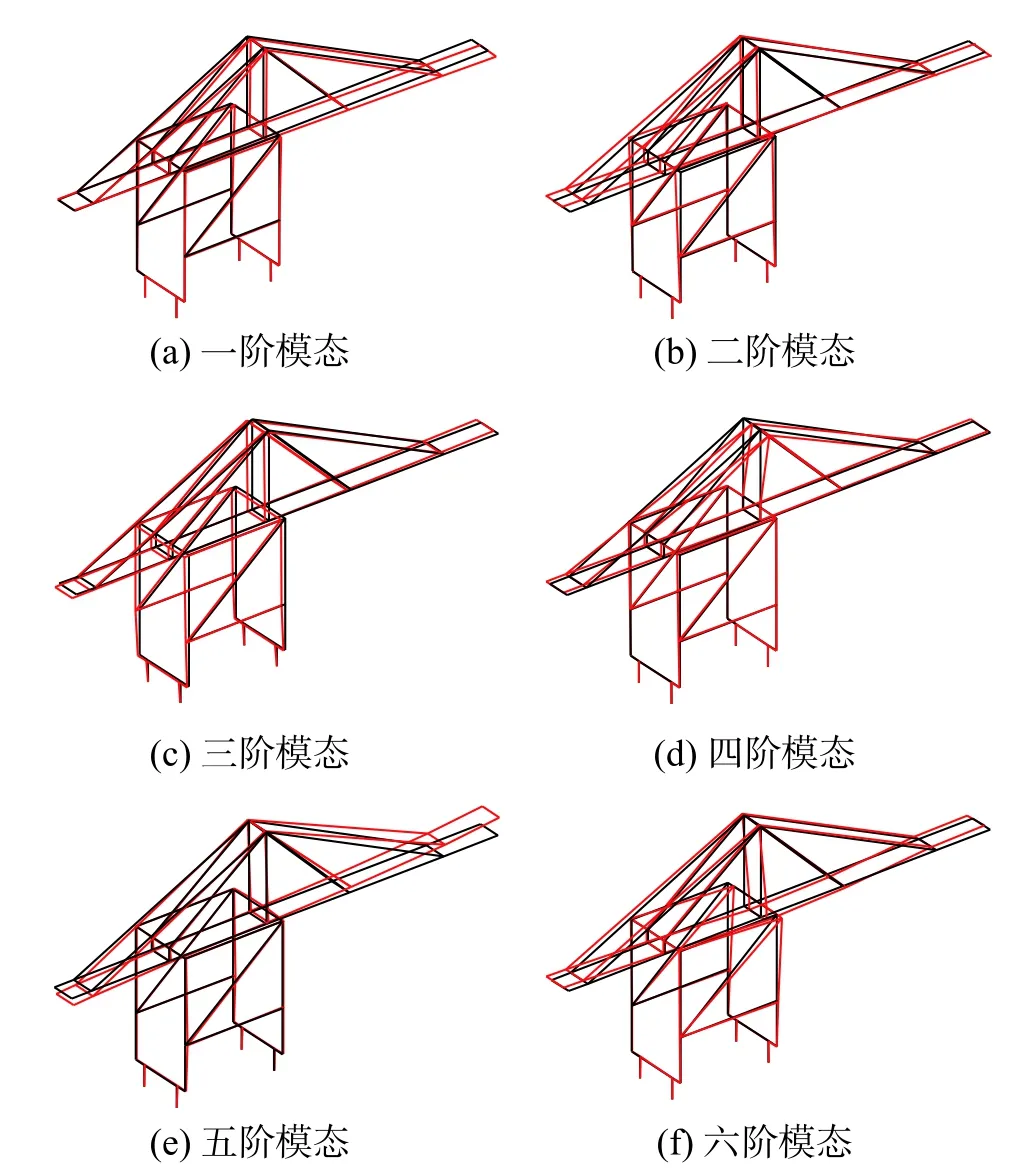
图 9 起重机不同阶模态响应Fig.9 Different modal responses of crane
图10为施加地震荷载之前有/无起重机时桩排1中不同桩(分别对应图2中的桩A1~F1)的轴力剖面对比图。从图中可以看出,没有起重机时,地震前桩排1全部受压(注:桩的轴力以拉为正,以压为负)。桩身未嵌入土层部分,即自由段部分,受桩自重的影响,轴力自桩顶随高程的减小呈现均匀增大的趋势。桩顶位置处桩的轴力并不为零,主要受上部结构的自重的影响。事实上,全部桩在桩顶位置所受轴力之和为上部码头面板的自重。嵌入土层的桩,因不同埋深处土质不同,桩侧摩阻力随之发生变化,受桩侧摩阻力和桩自重的影响,轴力随高程的减小呈现先增大后减小的趋势,且各桩在同一土层中轴力的变化趋势相同。考虑起重机后,起重机重量沿腿部接触点传递至面板,再由面板传递至各桩。桩A1~E1的轴力均增大,而桩F1的轴力减小,此时桩F1受拉,其余各桩受压。A排桩的埋深最小(即自由长度最长),虽然桩的数量较B~D排多,但土弹簧分布数量(即桩-土接触总面积)远远小于E和F排。如此,在自重下,结构整体朝海侧倾斜,F排相对向上移动,轴力减小。

图 10 地震前桩的轴力剖面Fig.10 Axial force profile on pile before shaking
考虑到码头面板足够刚,所以水平地震荷载作用下面板各点呈现相同的水平位移。图11为地震作用下有/无起重机,面板地震位移响应时程。在地震刚开始阶段(0 s~2 s时间段内),输入加速度相对较低,面板位移较小。随着加速度的增加,面板位移逐渐增大。当输入加速度达到峰值并逐渐衰退,面板位移达到峰值逐渐降低。15 s后输入加速度几乎为0,此时面板呈现自由振动,由于体系阻尼的存在,面板呈现出近似稳态的振动衰减。由图11可知,当没有起重机时,地震中面板最大位移为0.33 m,出现在3 s左右。考虑起重机后,面板最大位移为0.37 m,出现在7 s左右。由此可见,考虑起重机作用后,增大了地震中面板的最大位移,且最大位移出现时刻较无起重机情况有所推后。类似地,地震结束时刻,无起重机时,面板最大位移为0.05 m;有起重机时,面板最大位移为0.14 m。总体来说,在地震作用下,起重机的存在明显增大了面板的位移。图12为面板位移最大和地震结束两个典型时刻的下部码头结构变形情况。从图中可以看出,在两个典型时刻下,起重机的存在增大了码头结构的变形,变形增大程度随高程的增加而增大。下面将针对面板位移最大和地震结束两个典型时刻的计算结果进行分析。
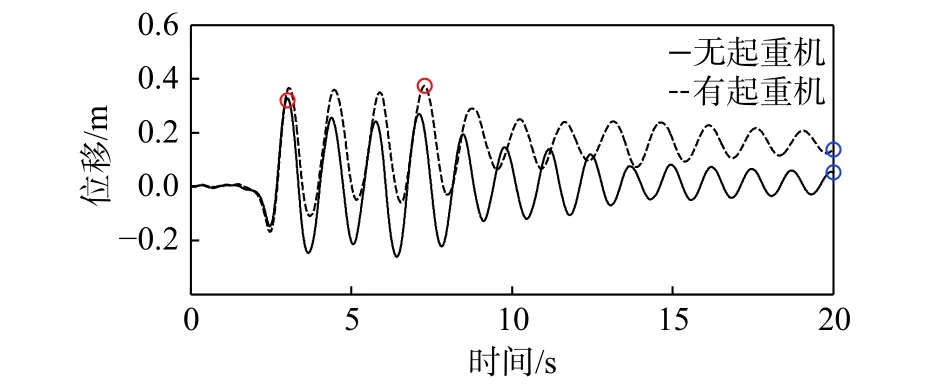
图 11 面板位移响应时程Fig.11 Displacement time history response of deck
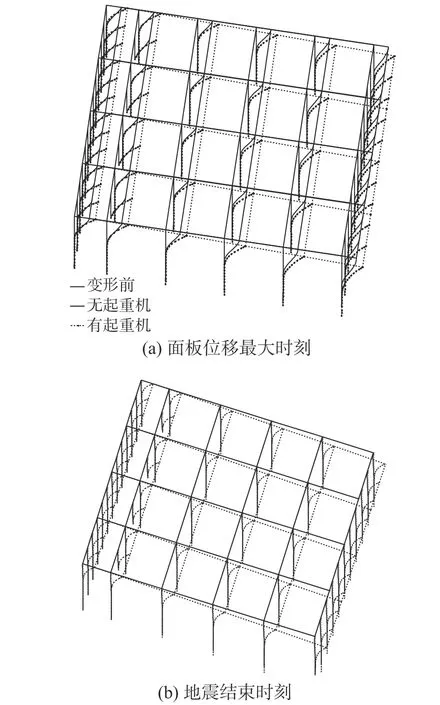
图 12 地震中典型时刻码头结构变形(放大系数:5)Fig.12 Wharf structure deformation at typical time instant during shaking (factor of 5)
图13为施加地震后两个典型时刻有/无起重机时桩身位移剖面。从图中可以看出,在两个典型时刻,有/无起重机码头桩基的位移均在软粘土层(IIIA层)及以上产生更明显的变化趋势。在面板位移最大时刻,考虑起重机的存在,明显增大了桩顶的位移。在地震结束时刻,起重机的存在,对软粘土层以下的影响较小,对软粘土层及以上的影响较大,且影响程度随桩身高程的增加而增大。
图14为施加地震后两个典型时刻有/无起重机时桩身轴力剖面。从图中可以看出,在水平地震作用下,桩轴力变化趋势及大小与地震前大致相同。在两个典型时刻,由于起重机的存在,除桩F1外,其余桩的轴力明显大于无起重机时的轴力。桩D1~F1的轴力最大值出现在软粘土层附近,而桩A1~C1的轴力最大值出现在坡面的碎石层附近,产生这种差别的原因可能是由于起重机的腿部在地震过程中发生左右摆动导致桩面板发生了内力重分布,进而影响了桩的轴力分布。
进一步,考虑到结构的对称性,在此取两榀即前27根桩(见图2(a))进行轴力分析。图15为施加地震后两个典型时刻有/无起重机时桩身最大轴力对比。由图可知,除F排桩与E排短桩的轴力最大值为正值(即受拉状态)外,其余桩的轴力最大值均为负值(即受压状态),且短桩在有/无起重机情况下的轴力最大值相差不大。除F排桩外,其余桩的轴力最大值均因起重机的存在而变大。
图16为施加地震后两个典型时刻有/无起重机时桩身剪力剖面。从图中可以看出,两个典型时刻,有/无起重机,桩在软粘土层以下的剪力变化不明显,其剪力变化位置主要在软粘土层及以上。不考虑起重机时,在面板位移达到最大时刻,桩F1和E1的剪力最大值出现在地表附近,桩A1~D1的剪力最大值出现在软粘土层处;在地震结束时刻,剪力的变化趋势与面板位移最大时刻相反,桩A1~F1的剪力最大值衰减率达80%~85%。考虑起重机作用后,在面板位移达到最大时刻,剪力最大值出现的位置大致没变,但变化幅度整体变小;在地震结束时刻,剪力的变化趋势与面板位移最大时刻相似,桩A1~F1的剪力最大值衰减率达60%~80%。
图17为施加地震后两个典型时刻有/无起重机时桩身最大剪力对比。由图可知,在面板位移最大时刻,起重机的存在使其剪力最大值变小;在地震结束时刻,起重机的存在使其剪力最大值变大,这可能与地震结束后引起的桩上较大位移有关。
图18为施加地震后两个典型时刻有/无起重机时桩身弯矩剖面。从图中可以看出,在面板位移达到最大时刻,未考虑起重机时,软粘土层以下的弯矩变化较小,软粘土层及以上的弯矩变化显著,这与上面的剪力图是相对应的。弯矩极值位置出现在软粘土层与硬粘土层界面处和桩与面板连接处;考虑起重机后,桩A1~D1的桩顶呈现正向的最大弯矩,桩F1和E1的桩顶呈现负向的最大弯矩,除桩F1外,其余桩弯矩最大值点位置均发生变化,桩A1和B1的弯矩最大值点位置由原来的软粘土层变为桩顶。在地震结束时刻,未考虑起重机时,在软粘土层与硬粘土层界面处和桩与面板连接处存在较大的残余弯矩;考虑起重机后,越靠近海侧,其桩顶残余弯矩越大。
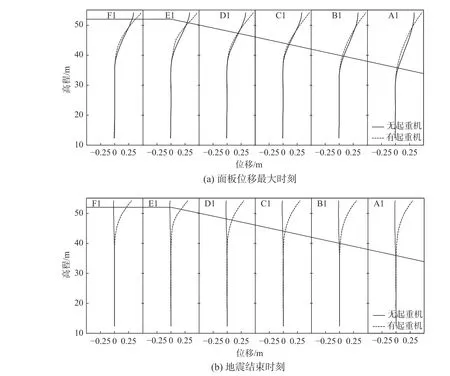
图 13 地震中典型时刻桩的位移剖面Fig.13 Pile displacement profile at typical time instant during shaking
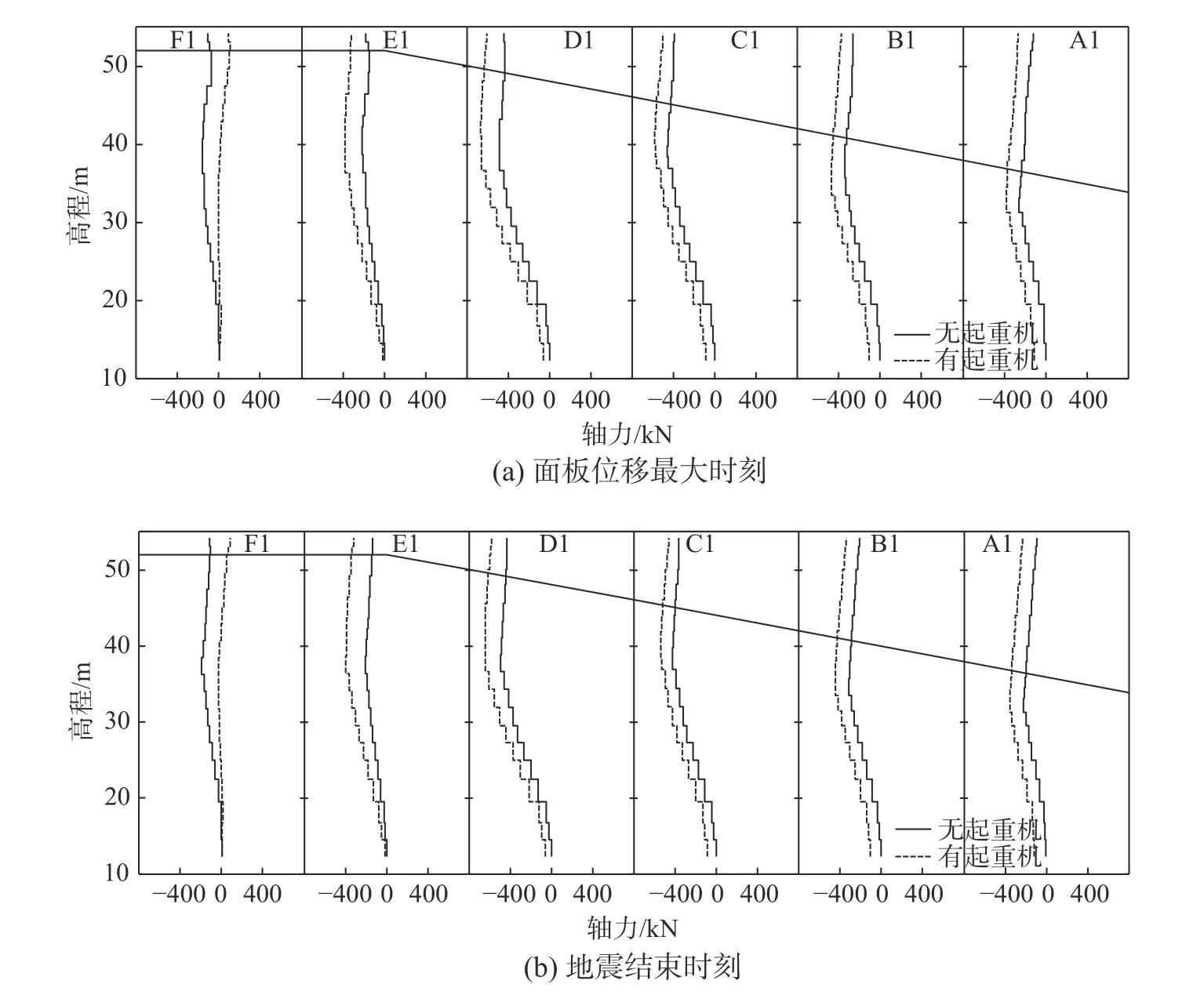
图 14 地震中典型时刻桩的轴力剖面Fig.14 Axial force profile on pile at typical time instant during shaking
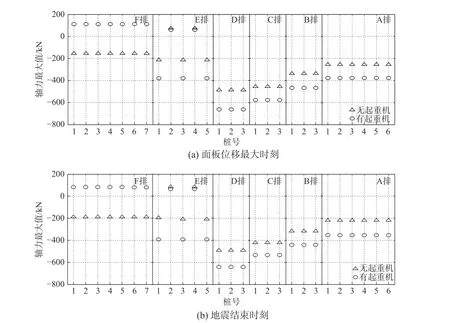
图 15 地震中典型时刻桩的轴力最大值Fig.15 Maximum of axial force on pile at typical time instant during shaking

图 16 地震中典型时刻桩的剪力剖面Fig.16 Shear force profile on pile at typical time instant during shaking
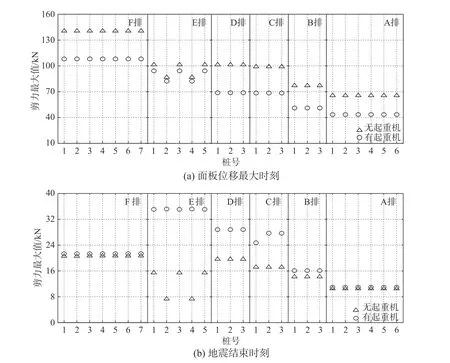
图 17 地震中典型时刻桩的剪力最大值Fig.17 Maximum of shear force on pile at typical time instant during shaking
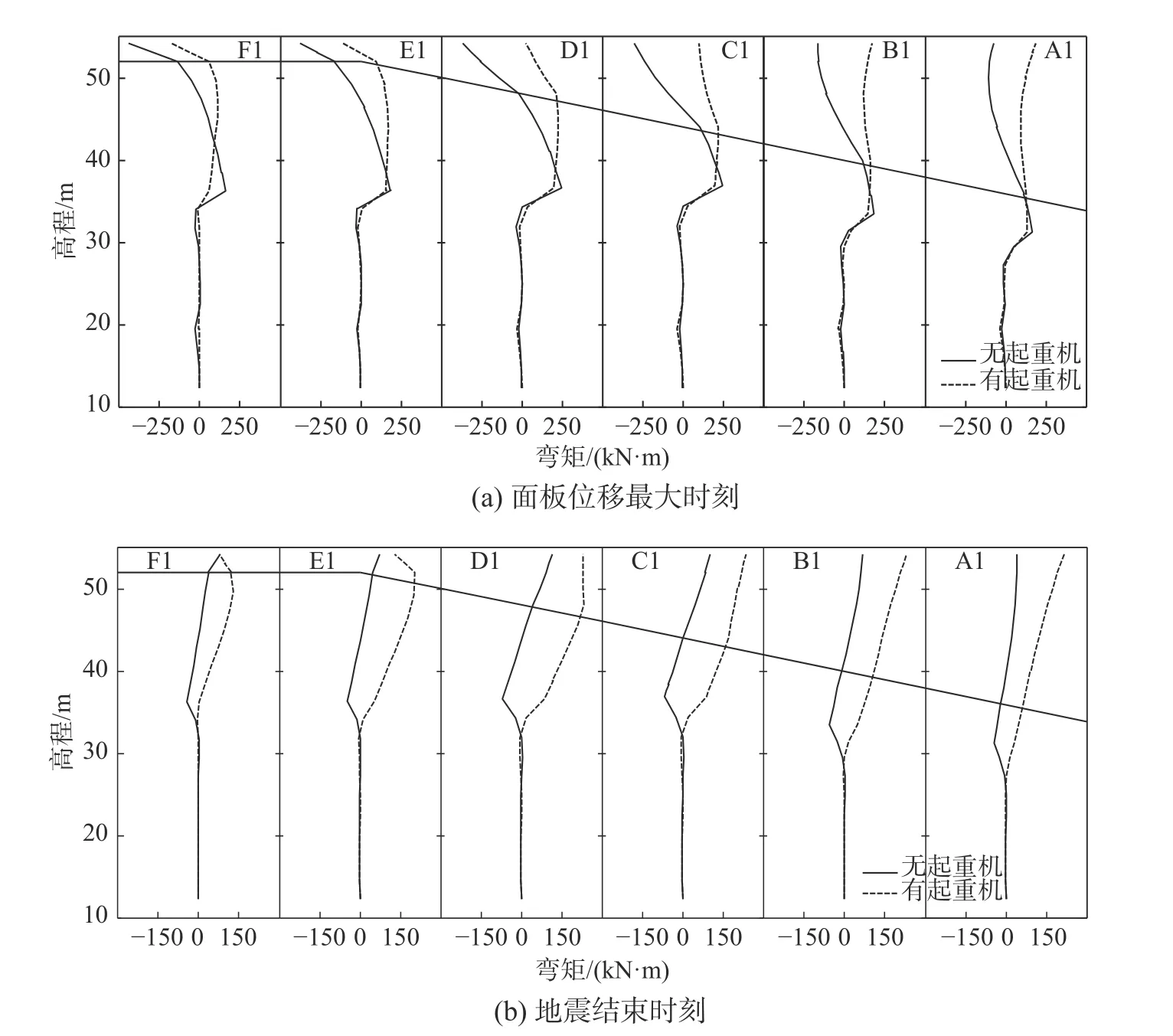
图 18 地震中典型时刻桩的弯矩剖面Fig.18 Bending moment profile on pile at typical time instant during shaking
图19为施加地震后两个典型时刻有/无起重机时桩身最大弯矩对比。值得说明的是,这里仅关注弯矩大小,并未关注弯矩方向。由图可知,在两个典型时刻,桩的弯矩最大值变化规律与剪力最大值的变化规律相似,在此不再赘述。
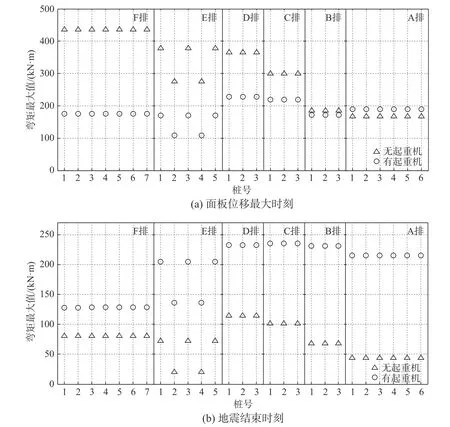
图 19 地震中典型时刻桩的弯矩最大值Fig.19 Maximum of bending moment on pile at typical time instant during shaking
3 结论
本文通过建立起重机及起重机-码头结构相互作用三维有限元模型,研究了起重机对码头结构的动力响应影响,针对起重机对下部码头桩基位移、轴力、剪力、弯矩响应的影响,得到以下结论:
(1) 起重机的存在,改变了下部码头桩基的内力分布和增加了面板的位移。起重机的重心偏向前大梁(即海侧),导致各排桩之间所受起重机传递的重力不同。由于土弹簧分布和特性与桩的埋深和土层分布有关,每排桩的侧摩阻力与土的侧向抗力不同,使得桩-土相互作用更加复杂,最终导致每排桩的轴力变化幅度不一致。根据各桩的受力情况,特别是地震中桩基出现受拉情况,设计时应格外注意陆侧桩及短桩的设计。
(2) 由于软粘土层的存在,桩在土层软硬交界面处剪力与弯矩出现较大变化。考虑起重机后,对剪力最大值出现的位置影响不大,但对弯矩最大值的位置影响较大,进而会影响码头结构的破坏机制。起重机的存在使得面板位移最大时刻的剪力与弯矩最大值减小,并增加了地震结束后的残余剪力与弯矩。总体来说,在地震作用下起重机的动力行为,尤其是起重机腿部朝海陆两侧的左右摇摆,对下部码头结构的动力响应影响较大,该影响在较弱土层(软粘土层)以上表现的更为明显。

