解析型几何非线性圆拱单元

丁 敏，石家华，王斌泰，王宏志，邓 婷,2，罗 双,3，蒋秀根

(1. 中国农业大学水利与土木工程学院，北京 100083；2. 唐山市路北区凤凰新城管委会，河北，唐山 064400；3. 中国农业科学院基本建设局，北京 100081)

圆拱作为一种压弯结构，由于轴线曲率的影响，使得轴力与弯矩相互耦合，其截面内力以轴力为主、同时存在弯矩及剪力。一方面在实际工程中，由于拱结构的长细比较大[1]，截面刚度较小，为保证拱结构内力和位移计算结果的精确性，研究中考虑杆件几何非线性影响是十分必要的；另一方面由于拱截面内力以轴压力为主，弯矩及剪力为辅，拱发生失稳破坏是一种常见的破坏形式，而拱结构失稳破坏是典型的非线性问题。

拱的失稳破坏具有突然性，如极值点失稳、分岔失稳，拱结构稳定性是影响其安全性的重要因素之一[2−10]。圆拱由于受面内荷载易发生平面内失稳，当拱在平面内荷载作用下，所承受的荷载达到一定的临界值时，拱的平衡状态会发生突然性的改变，拱轴线离开原来的变形状态，向平面挠曲状态转化，从而丧失稳定性[11−13]。平面内失稳可分为平面内分岔失稳与平面内极值点失稳，而结构只有在径向均布荷载作用下且忽略轴向变形时，才会发生分岔失稳[14]。因此在分析圆拱结构几何非线性问题时应考虑是否忽略轴向变形：忽略轴向变形的无压缩模型可进行分岔失稳分析，考虑轴向变形的可压缩模型可进行极值点失稳分析。

对于圆拱的几何非线性问题，国内外学者采用静力法、能量法和有限元法等建立了各类几何非线性圆拱模型，求解相应问题。Timoshenko[15]考虑几何非线性对结构的影响，建立了受压圆环和曲杆的屈曲分析模型，从物理方程出发得到了二阶弯曲挠度位移微分方程，结合圆拱边界条件求出了精确的圆拱分岔失稳特征方程及临界荷载。Dinnik[16]在均布静水压力作用下的圆拱研究中，运用力法先求出内力的表达式，再根据物理方程、几何方程求出位移表达式，进而根据边界条件得到了不同支座情况下的失稳临界荷载。项海帆[14]分析了圆拱的平面内屈曲问题，详细列出了无铰拱、两铰拱以及三铰拱在不同弧心角时的临界荷载系数。邓婷[11]基于静力法基本方程求得了考虑轴力产生的二阶效应的几何非线性圆拱位移及内力解析表达式，以矩阵形式的直接刚度法构造了有限单元，并用静力法进行了分岔失稳分析。申波等[17]利用小变形理论及ANSYS 研究了均匀径向压力作用下深圆拱的平面内稳定性，从微段平衡方程入手，计算得到了轴向位移通解。程鹏、童根树[18]依据平截面假定，采用有限变形理论中的应变位移关系，完整地考虑了横向应力和剪应力的二阶效应，用虚功原理推导了拱平面内非线性分析的平衡方程，给出了圆弧拱平面内弯曲失稳一般理论。可见，研究主要集中在特定工况下圆拱结构稳定问题的解析解方面，对于任意工况下圆拱结构的内力、位移和稳定分析尚缺乏统一模型。本课题组提出了解析形函数法[19−22]，该方法综合了静力法、能量法及有限元法的优点，是一种高精度高效率的研究方法，可用较少的单元精确分析复杂结构复杂荷载的问题。

本文以圆拱为研究对象，采用解析形函数法，基于小变形、大挠度假定，考虑轴力引起杆件二阶弯矩的几何非线性影响，在静力法位移方程的基础上，构造了圆拱解析形函数，结合能量法及势能变分原理，构造解析型几何非线性圆拱单元，采用本单元模型对圆拱的平面内分岔失稳和极值点失稳进行对比分析，验证本构造单元的精确性、可行性和适用性。

1 模型及假定

1.1 模型参数

建立随动极坐标系，圆拱坐标系及内力方向如图1所示。按右手螺旋法则定义坐标系，坐标原点位于拱左端，轴向坐标x为圆拱轴线方向，向右为正，z轴为圆拱径向方向，位于圆拱轴线平面内，垂直于轴线，指向圆心为正。

圆拱参数：轴线为平面圆弧，其半径为r，弧长为l，圆心角为θ ，且l=rθ。

圆拱荷载：轴向均布荷载qx、径向均布荷载qz、均布力矩my，xi处轴向集中力Pxi、径向集中力Pzi及集中力矩Myi，与坐标轴方向一致为正。

圆拱位移：轴向位移u、径向位移w和转角β，与坐标轴方向一致为正。

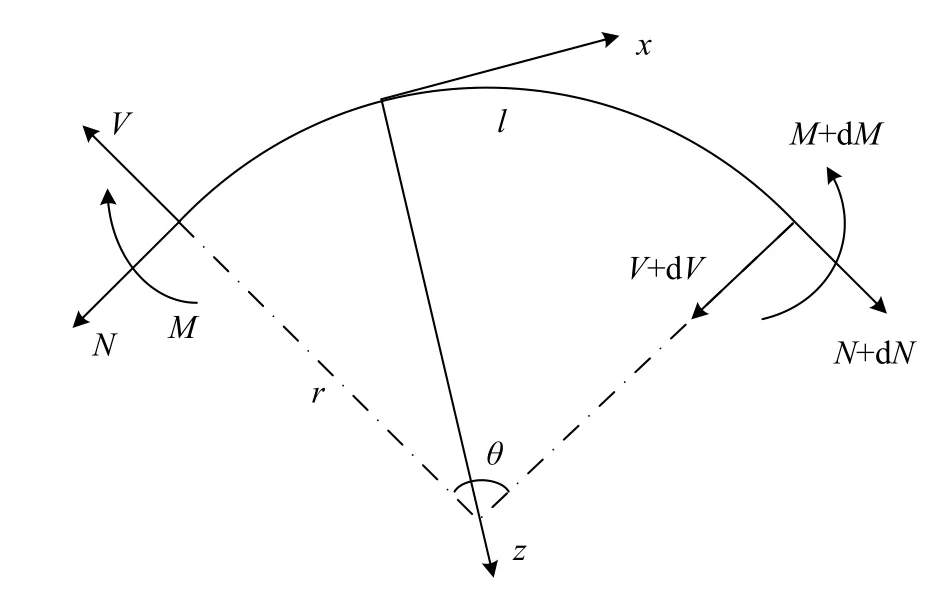
图 1 圆拱坐标系及内力Fig.1 Coordinate system and internal force of circular arch

圆拱内力：轴力N、剪力V和弯矩M，当截面外法线方向与坐标轴方向一致时，定义为与坐标轴方向一致为正；当截面外法线方向与坐标轴正向相反时，内力定义为与坐标轴方向相反为负。

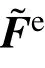
δe={u1w1β1u2w2β2}T;

Fe={N1V1M1N2V2M2}T。

1.2 基本假定

本文推导过程基于以下假定：

1)圆拱轴线为等曲率平曲圆弧；

2)将圆拱视为细长杆，忽略剪切变形，可采用Euler-Bernoulli弯曲理论计算截面的弯曲应力及弯曲变形；

3)圆拱截面按等截面考虑，对于变截面圆拱，可将其划分或简化为若干个等截面圆拱段；

4)圆拱为线弹性变形，圆拱的抗压刚度EA及抗弯刚度EI均为常数，圆拱截面内力与变形成正比；

5)符合大挠度假定，考虑轴力产生的二阶效应，即P-Δ效应。

2 单元位移形函数

2.1 位移控制方程

综合圆拱平衡方程、几何方程及物理方程[11]，可得位移控制方程：

1)轴向位移控制方程

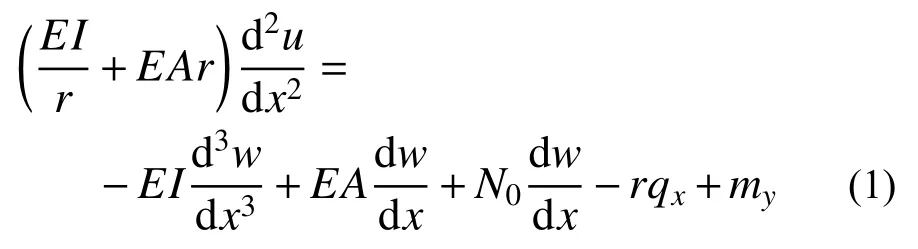
式中：E为材料弹性模量；A为截面面积；I为截面惯性矩。

2)径向位移控制方程

2.2 位移方程

对位移控制方程式(1)～式(3)求解关于径向位移w和轴向位移u的齐次微分方程，可得[11]：

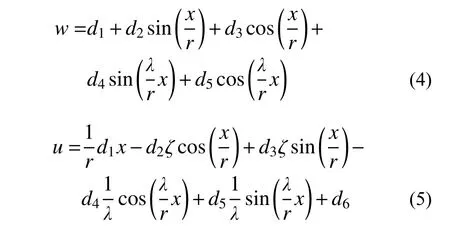
2.3 位移基函数向量及导函数转换矩阵

1)位移基函数向量

将式(4)和式(5)写成关于位移系数的向量表达，可得位移向量表达式：

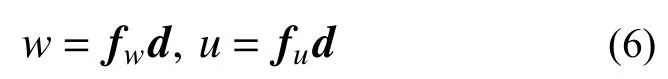
式中：d为位移系数向量，且d={d1d2d3d4d5d6}T；fw、fu分别为径向和轴向位移基函数向量，且：

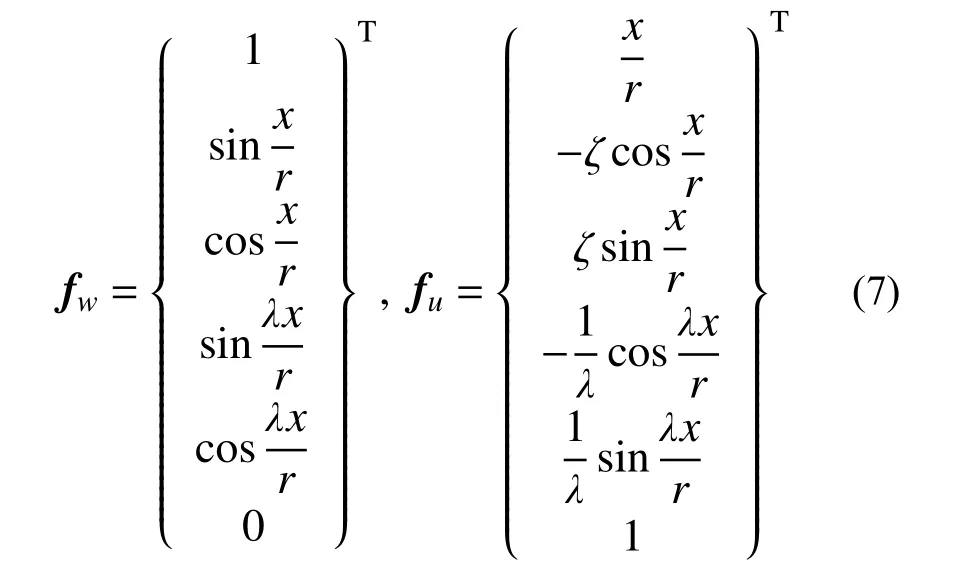
2)导函数转换矩阵

使用导函数转换矩阵Z来表述基函数导数f′与基函数f的关系，有：

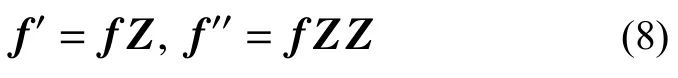
结合式(7)可得，径向与轴向位移基函数向量的导数转换矩阵一致，且为：

2.4 单元位移形函数

根据两端节点几何边界条件，可得：

δe={u(0)w(0)β(0)u(l)w(l)β(l)}T

写成：

式中，A为节点位移矩阵，且：

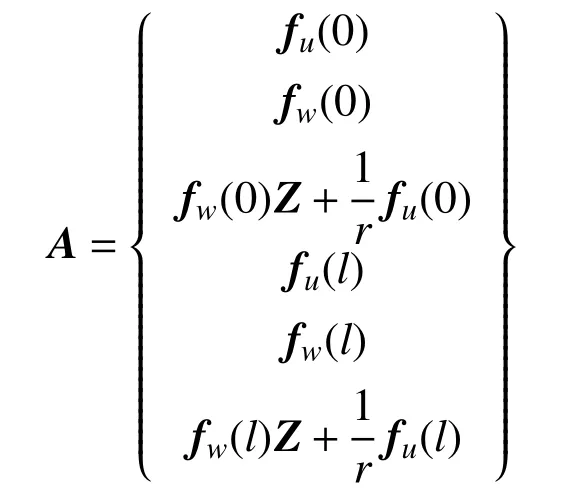
根据式(10)，其位移方程式(6)可改写为：

定义w=Nwδe，u=Nuδe，可得：

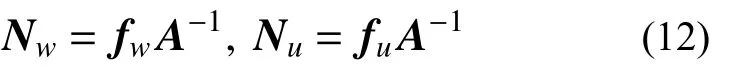
式中，Nw、Nu分别为径向和轴向位移形函数。

同时根据几何方程[11]，代入位移形函数式(12)，可得轴向应变ε、弯曲转角 β和弯曲曲率κ表达如下：

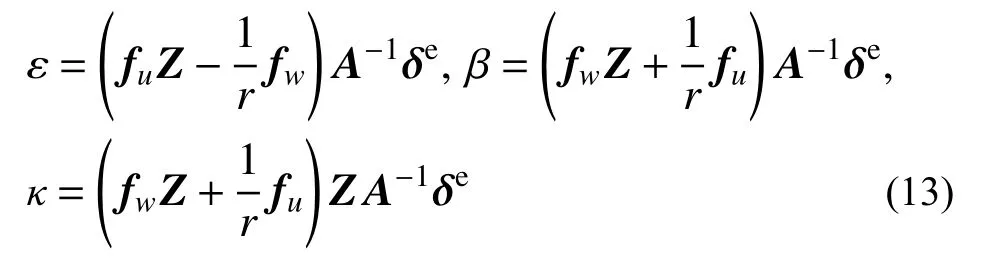
3 可压缩圆拱势能及单元

3.1 单元势能一般式

平面圆拱结构承受荷载时，单元总势能包括变形能和荷载势能。变形能包括压缩变形能和弯曲变形能；当考虑轴力产生的二阶效应时，荷载势能包括外荷载势能和杆端轴力势能。单元总势能可写成下列形式[23]：

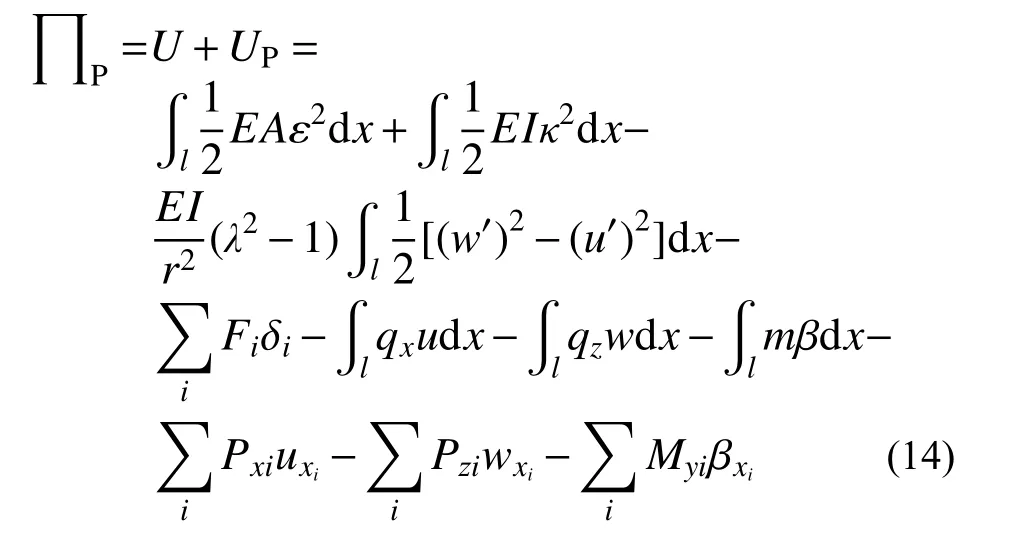
式中：U为单元的变形能；Up为荷载势能。

3.2 单元势能变分

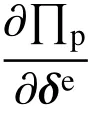
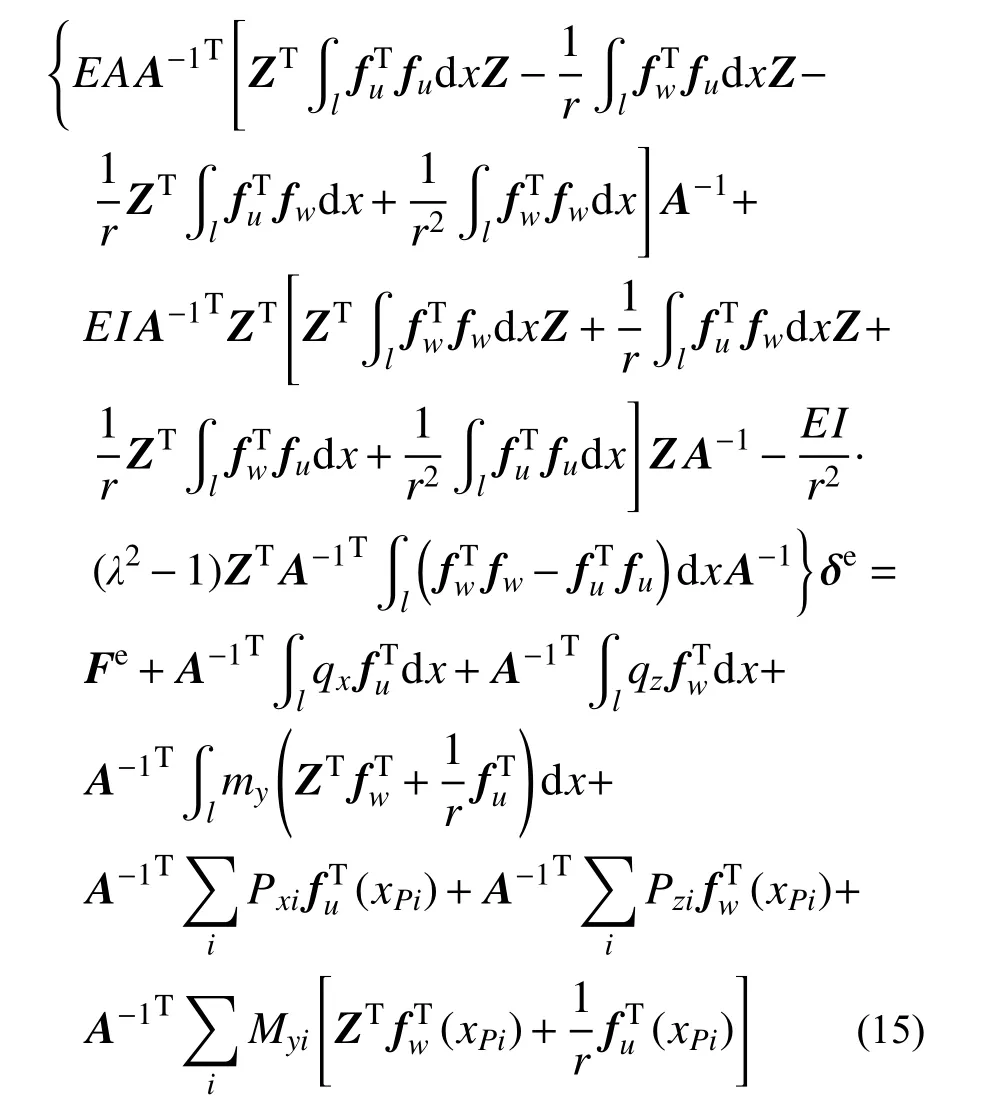
3.3 单元列式

1)等效平衡方程

将式(15)改写，即可得以单元节点位移表达的圆拱等效平衡方程：

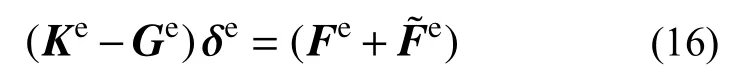
2)单元刚度矩阵

根据等效平衡方程式(15)与式(16)对应，可得单元刚度矩阵具体表达列式：

式中：KN为抗压刚度矩阵；KM为抗弯刚度矩阵。且：

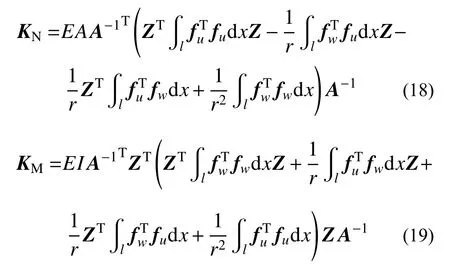
3)几何刚度矩阵

几何刚度矩阵可表达为：

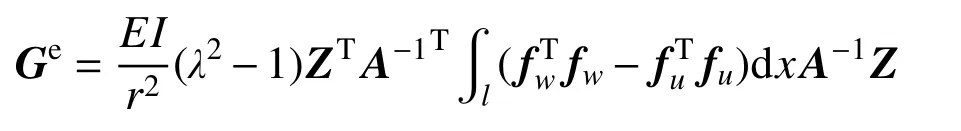
4)等效节点力向量

等效节点向量可表达为：

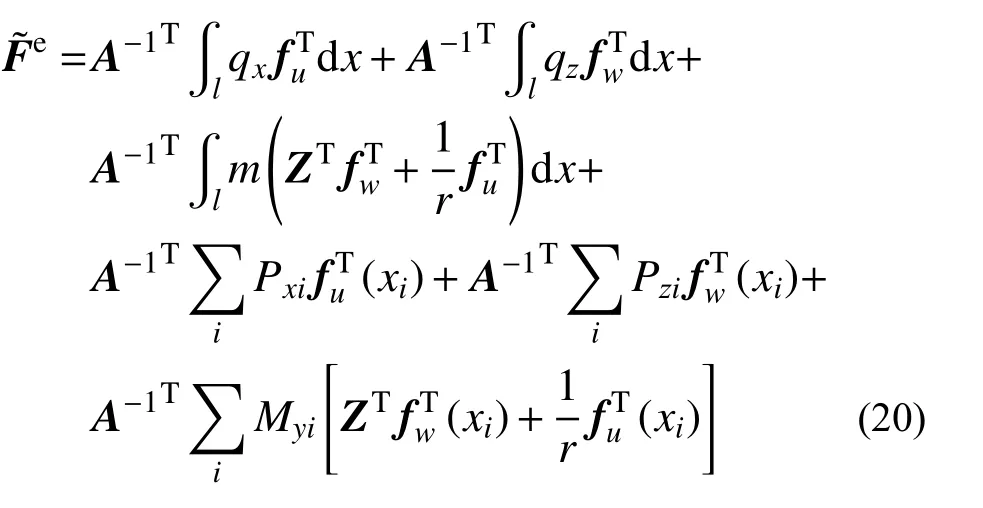
4 无压缩圆拱单元

在圆拱结构实际工程中，由于轴向压力的存在，需考虑其稳定问题，不考虑轴向变形的无压缩圆拱模型可用于分析圆拱结构的分岔失稳问题，因此本文在以上模型的基础上，继续构建无压缩圆拱单元，为后续圆拱结构稳定问题的研究做准备。

一般来说，构建无压缩圆拱单元，可采用直接模型和退化模型两种途径。直接模型可基于本文模型的构建过程由 ε=0重新推导而得；退化模型可基于本文模型单元列式由EA=∞退化而得。如下是采用退化模型得到的无压缩圆拱单元。

4.1 位移基函数及导数

1)位移参数

取EA=∞，代入位移参数

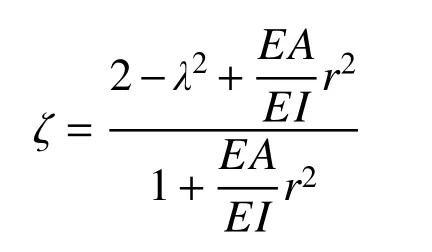
有：

2)位移基函数

取EA=∞，结合式(7)与式(21)，可得无压缩圆拱的位移基函数为：

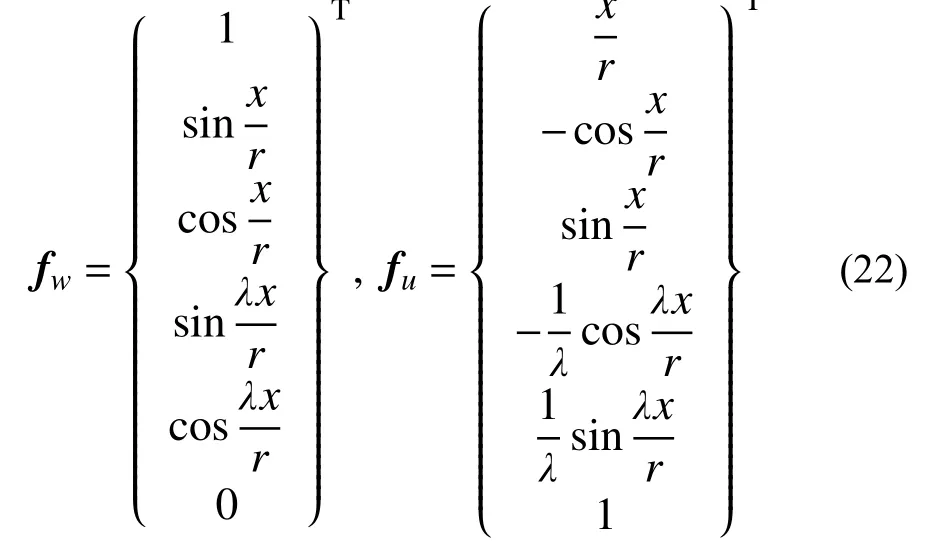
3)导数转换矩阵

取EA=∞代入式(9)，可得无压缩圆拱基函数的导数转换矩阵为：

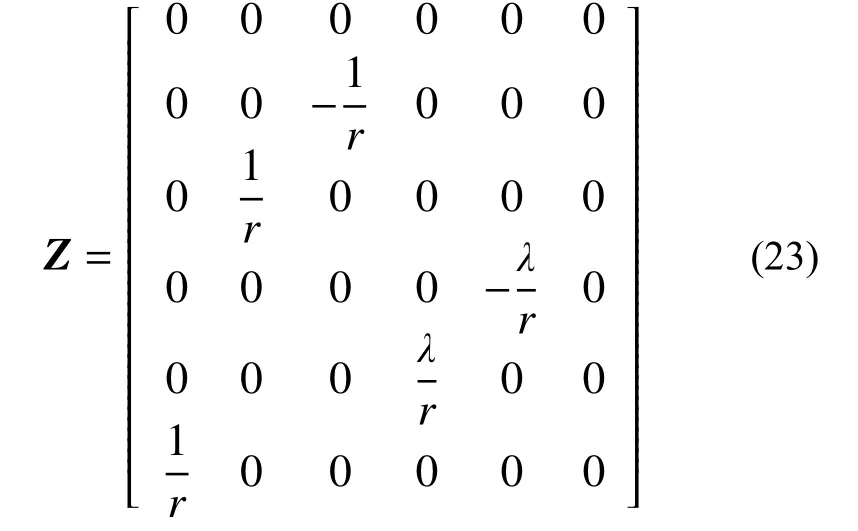
4.2 抗压刚度矩阵

将式(18)抗压刚度矩阵作如下改写：

代入式(7)和式(9)计算，可得：

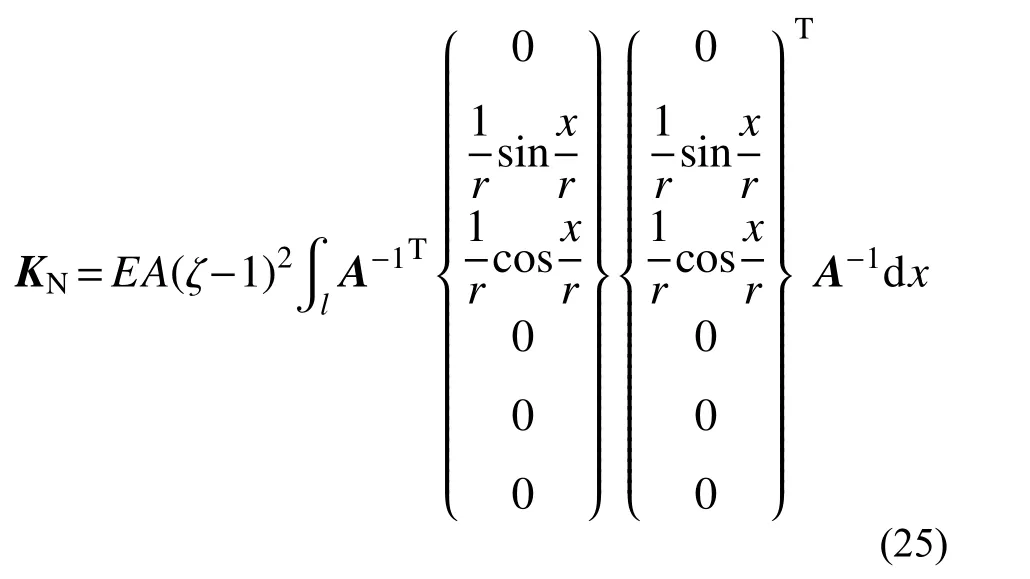
取EA=∞代入式(25)，可得到无压缩圆拱抗压刚度矩阵为：

4.3 单元列式

1)等效平衡方程

由式(16)，可得无压缩圆拱等效平衡方程：

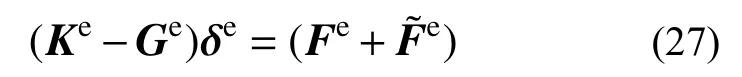
2)单元刚度矩阵

无压缩模型单元刚度矩阵一般式形式上同式(17)，同时理论上取EA=∞，可得简化式。

将式(22)、式(23)和式(26)代入式(17)和式(19)，可得无压缩圆拱的单元刚度矩阵：

式中，KM表达式同式(19)。

3)等效节点力向量

将式(22)和式(23)代入式(20)，可得无压缩圆拱等效节点力向量，其表达式同式(20)。

4.4 模型对比分析

经按本文构建过程重新推导得到直接模型，通过对比可知，由本文模型理论退化得到的无压缩圆拱单元模型与直接模型是一致的。在理论上，当EA=∞时，用本文模型计算无压缩圆拱具有可行性和正确性。

退化模型与直接模型的结果一致，说明本文模型单元的准确性与适用性。

5 算例及对比

5.1 圆拱平面内分岔失稳分析

5.1.1 分岔失稳分析方法

结构只有在径向均布荷载qz作用下且忽略轴向变形时，才会发生分岔失稳[14]。对于分岔失稳，等效平衡方程式(27)有不确定解，其位移系数行列式为0，即：

根据式(29)可求得圆拱在各种约束作用下的平面内分岔失稳的最小特征值λcr。

5.1.2 分岔失稳临界荷载

由特征值λcr求解可得临界轴力Ncr。对于圆拱分岔失稳临界状态，有：Ncr=rqcr[11]，则分岔失稳临界荷载为：

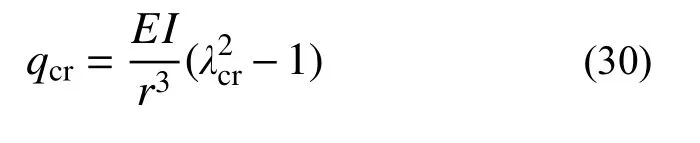
定义临界荷载系数k：

有临界荷载：

5.1.3 不同结构形式的分岔失稳分析

采用本单元模型分别对无铰拱、单铰拱、两铰拱、三铰拱及左固右铰拱五种结构形式的圆拱进行分岔失稳分析，求得不同圆心角角度下的分岔失稳最小特征值λcr和临界荷载系数k，计算结果见表1。

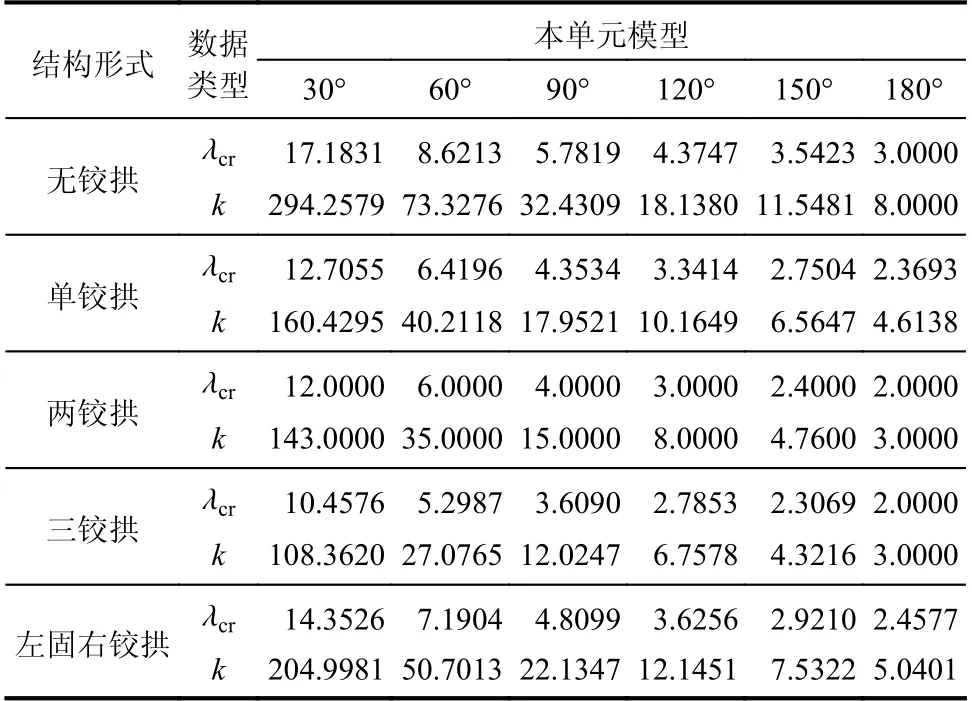
表 1 圆拱分岔失稳特征值及临界荷载系数Table 1 Bifurcation instability eigenvalues and critical load coefficients of circular arches

5.1.4 对比与分析

为验证构造单元的精确性，将本单元分岔失稳分析结果与经典模型(Timoshenko模型[15]、Dinnik模型[16])、静力法模型[11]进行对比，给出与经典模型临界荷载系数的相对误差，其中左固右铰拱没有经典模型结果，给出与静力法模型结果对比，对比结果见表2。

由表2看出，本文构造的非线性圆拱单元进行分岔失稳分析得到的失稳临界荷载系数与经典模型、静力法模型计算结果一致，相对误差为0%，这说明了本单元模型的精确性及运用本单元模型进行分岔失稳分析的可行性。可见，采用静力法获得解析解的经典模型，仅适用于特定工况下圆拱结构的平面内分岔稳定分析，而采用能量法建立的本文单元则适用于任意工况下圆拱结构的平面内分岔稳定分析。

同时可以看出各结构形式随着圆心角角度增大，其失稳临界荷载系数变小；对于同一圆心角角度，上述五种结构形式，无铰拱的失稳临界荷载系数最大，稳定性最好，符合工程实际。

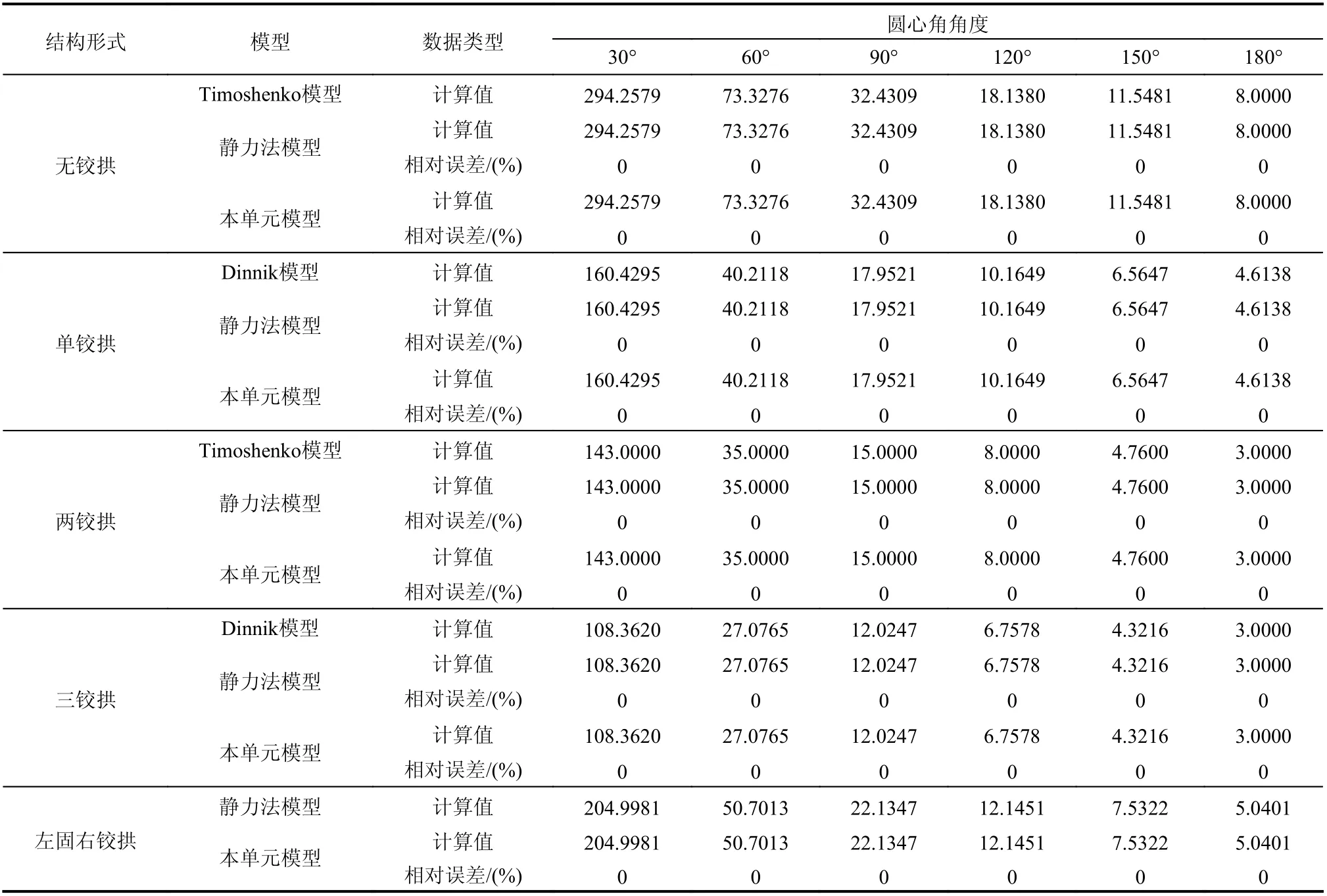
表 2 不同模型圆拱的分岔失稳临界荷载系数对比Table 2 Comparison of critical load coefficients for bifurcation instability of circular arches with different models

5.2 圆拱平面外极值点失稳分析

对径向均布荷载作用下的无铰拱进行平面内极值点失稳分析。假定无铰拱圆心角为120°，半径为5 m，截面尺寸为400 mm×400 mm，弹性模量为206 GPa，受径向均布荷载qz=10 kN/m。通过改变轴力特征值大小，求出跨中挠度，得到圆拱轴力特征值与跨中挠度变化曲线如图2所示。

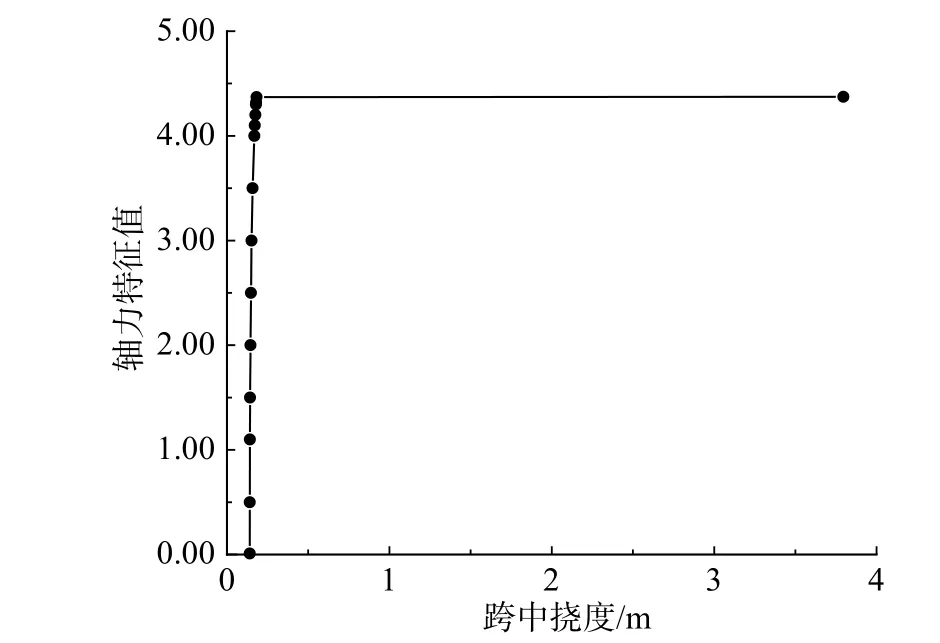
图 2 轴力特征值-跨中挠度曲线Fig.2 Axial force eigenvalue vs. mid-span deflection curve

由图2可见，当荷载达到临界荷载时，圆拱出现极值点失稳现象，且圆拱极值点失稳临界荷载与圆拱平面内分岔失稳临界荷载值相同。

上述所有算例表明：本文构造单元既可用于圆拱几何非线性的位移和内力分析，也可用于圆拱的平面内各类稳定分析。

6 结论

本文采用解析法构造了几何非线性圆拱单元，研究了圆拱结构几何非线性内力和位移计算以及平面内稳定分析问题，主要结论如下：

(1)基于圆拱几何非线性静力分析模型，构造了圆拱单元解析位移形函数。

(2)利用能量法，建立圆拱单元的势能，采用势能变分原理，得出等效平衡方程，给出单元刚度矩阵、几何刚度矩阵及等效节点力向量表达，构造了解析型几何非线性圆拱单元。

(3)通过理论上取EA=∞对本模型进行退化，得到不考虑轴向变形的无压缩圆拱模型，进而得到了解析型无压缩几何非线性圆拱单元，可应用于平面内分岔失稳分析。

(4)本文构造的解析型非线性圆拱单元可用于圆拱的平面内分岔失稳和极值点失稳分析。算例表明：本研究单元模型进行分岔失稳分析得到的失稳临界荷载系数与经典模型(Timoshenko模型、Dinnik模型)、静力法模型计算结果一致，误差为0%，这说明了本单元模型的精确性及运用本单元模型进行分岔失稳分析的可行性；平面内分岔失稳的临界荷载与平面内极值点失稳的临界荷载一致；本研究模型能够完整的呈现圆拱平面内由位移非线性发展到极值点失稳的过程。