半主动控制三维缩尺隔振楼板系统振动台试验研究

石运东，杜 洋，韩庆华，韦 鑫，吴 昊,3，刘铭劼，唐贞云

(1. 天津大学建筑工程学院，天津 300350；2. 滨海土木工程结构与安全教育部重点实验室(天津大学)，天津 300350；3. 中国地震局地震工程综合模拟与城乡抗震韧性重点实验室(天津大学)，天津 300350；4. 北京工业大学城市与工程安全减灾教育部重点实验室，北京 100124)

振动台已经成为地震工程领域应用最为广泛的试验工具之一[1]。近年来，中国、日本、美国等国家建成了大量振动台设备，为工程结构防灾减灾技术与理论的发展发挥了重要作用。地震工程领域的振动台一般使用出力能力较大的液压作动器。通过使用现代控制技术控制作动器出力，从而在振动台台体获得目标地震动。目前，振动台试验载重能力超过1000 t，作动器单方向总反力可达6000 t以上[1]。作动器的反力激发振动台基础的振动，并通过地基的传播引起振动台实验室以及周边建筑的振动。

随着大型工程结构振动台试验需求的增加以及液压技术与控制技术的发展，振动台的建设规模与数量逐步扩大，其振动问题也逐步受到研究人员的重视。国内刘必灯等[2−3]、Ren等[4]、肖汉[5]、张世忠[6]和李朝静[7]分别对防灾减灾学院3 m×3 m振动台，西南交大8 m×10 m振动台，同济大学四台阵系统，苏州科技大学6 m×8 m振动台等开展了现场实测与数值模拟计算。国外Luco等[8]对加州大学圣地亚哥分校的7.6 m×12.2 m户外振动台进行了振动测试。这些研究指出，振动台的振动虽然不会对结构安全造成影响，但可能影响实验室以及周边建筑结构内的机床以及精密仪器等的正常使用，也会降低建筑内人员的舒适度。为了降低振动台的振动影响，振动台建设需要考虑减振措施。具体可以在振源、振动传播过程以及目标建筑处进行控制。如通过增加振动台基础质量，可以从振源降低振动的影响。现有实践做法一般要求振动台的基础重量满足作动器最大激振力的50倍以降低振动影响。部分振动台通过建设隔振基础降低振动(如日本鹿岛技术研究所5 m×7 m振动台)。也可通过建设隔振沟等方式，在振动的传播过程中进行减振[3,9]。

另外，可以对周边建筑结构使用减隔振措施进行振动控制。目前，关于振动台试验引起的实验室与周边建筑结构振动的控制研究较少，相关技术多见于对工业设备振动、交通振动以及人行激励振动的减振控制[9−15]。然而，振动台引起的振动不同于一般的环境振动，传统减振措施用于振动台减振时存在一定局限性。振动台运动一般为三向运动，其引起的振动经过传播后也具有三维运动特性。再者，振动台工作频带范围较宽。目前建设的振动台，其频率一般可覆盖0.1 Hz～50 Hz，甚至达到100 Hz。研究人员进行科学研究时可能选择正弦波、实际记录地震动或者人工合成地震动等开展试验。由于试验目的以及试验模型等的不同，进行试验时地震动加载频率具有不确定性。作动器反力经过振动台基础、周围土体的传播至周边建筑结构基础，再传至结构上部时其振动特征复杂。

天津大学目前正在牵头建设“十三五”国家重大科技基础设施建设项目—“大型地震工程模拟研究设施”，振动台建设规模与功能都将对现有振动台有较大幅度的提升，振动台振动的影响成为重点研究的问题之一。大型振动台液压设备、管线等工艺布局将影响振动台基础的质量与刚度分布，造成振动台振动在基础内的传播规律复杂化。为降低振动台振动的影响，本文考虑振动台振动的频率不确定性以及三维振动的特点，提出了一种频率相关的变阻尼半主动控制方法，并基于此建立了半主动控制三维隔振楼板系统。本文通过振动台试验对该半主动控制系统进行研究。

1 半主动控制三维隔振楼板系统组成与设计

图1给出了半主动控制三维隔振楼板系统示意图。半主动控制三维隔振楼板系统由三维隔振子系统、半主动控制子系统以及浮置楼板子系统组成。

三维隔振子系统由竖向安装的螺旋弹簧实现三维隔振功能。半主动控制子系统由磁流变阻尼器、加速度计以及控制器组成。浮置楼板系统由钢龙骨与地板(静电地板或其它类型地板)组成。磁流变阻尼器连接结构楼板层与钢龙骨层输出半主动控制力。结构楼板层上安装三向加速度传感器进行振动信号采集，用于对控制算法所需要的频率信号进行检测。钢龙骨层、浮置楼板与周围的墙体、柱之间预留空隙，防止相互发生运动碰撞。

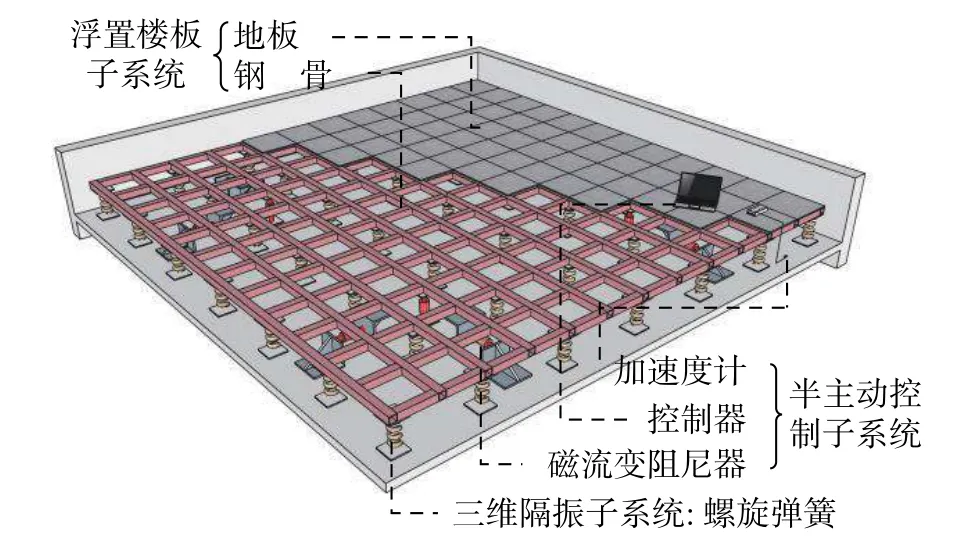
图 1 半主动控制三维隔振楼板系统示意图Fig.1 Semi-active controlled 3D floor isolation system

1.1 三维隔振子系统设计

三维隔振子系统通过竖向布置的螺旋弹簧实现。其水平向与竖向运动均按照单自由度体系设计。三维隔振子系统竖向刚度Kv与水平刚度Kh与弹簧数量、弹簧剪切模量、弹簧丝直径、弹簧直径、弹簧有效圈数、弹簧自由高度以及弹簧竖向压缩量有关[16]。由于环境振动引起的动位移较小，弹簧竖向压缩量δv按照静载作用下压缩计算：

式中：g为重力加速度；Tv为竖向运动周期。通过调整弹簧参数可实现需求设计周期[16]。为保证弹簧隔振支座的稳定性，需进行稳定性验算[16]。

1.2 半主动控制子系统设计

单质点体系受迫振动时，单一方向从输入绝对加速度到响应绝对加速度的传递率TR可表示为：

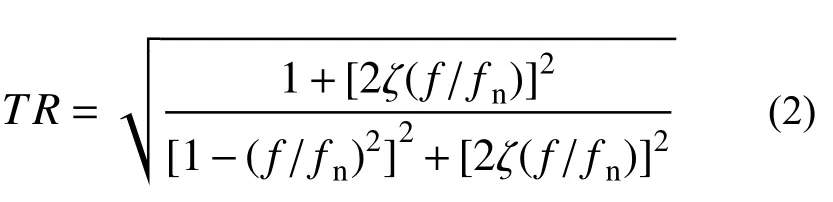
式中：f为激励频率；fn为体系固有频率；ζ为阻尼器所提供的阻尼比。图2为不同阻尼比(ζ)下频率比(f/fn)与传递率(TR)之间的关系。由图2可知，当f/fn>1.414时，降低阻尼比可以降低传递率；而当f/fn<1.414时，增加阻尼比可以降低传递率。

为实现振动台宽频振动时的最优控制，提出一种基于频率在线检测的on-off半主动控制方法，并通过磁流变阻尼器进行出力控制。on-off控制分为高阻尼力模式与低阻尼力模式，如式(3)所示：

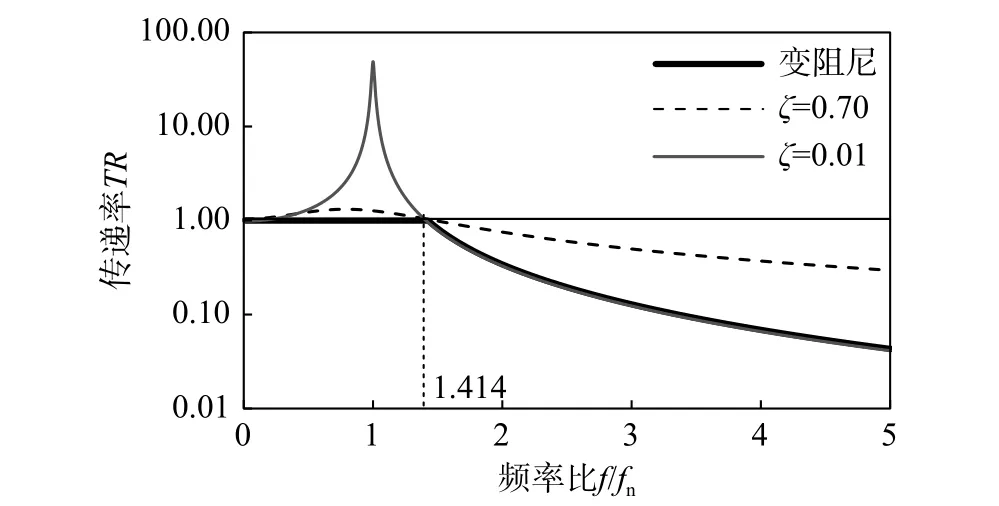
图 2 不同阻尼比时单质点体系加速度传递率Fig.2 Acceleration transmissibility for SDOF system with different damping ratio

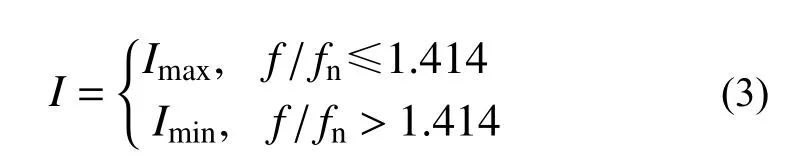
式中：I为控制电流；Imin与Imax分别为最小与最大控制电流。当激励频率满足f/fn≤1.414时，使用高阻尼力模式，通过控制磁流变阻尼器施加最大控制电流使其产生高阻尼力锁定浮置楼板。当激励频率满足f/fn>1.414时，使用低阻尼力模式，通过控制磁流变阻尼器施加最小控制电流使其产生低阻尼力释放浮置楼板。图2中的黑色粗实线给出了理想情况下加速度传递率与频率比关系。在三维隔振系统的三个方向上分别使用此方法进行控制。实际中，由于阻尼器控制信号在最大值与最小值之间变动，容易导致加速度出现较大变化。因此，计算所得阻尼器控制电流可通过低通滤波器过滤掉信号突变带来的高频控制信号。

设置半主动控制系统在检测到高于要求起控加速度u¨min的振动时才开始控制。未进行试验时，则对阻尼器输入最大控制电流Imax，保持隔振系统处于锁定状态。为确保所提出的on-off半主动控制效果，应确保阻尼器低出力模式时，浮置楼板惯性力可以克服阻尼器的最小出力；而高出力模式时，阻尼器最大出力应大于浮置楼板惯性力以锁定楼板。阻尼器在相对速度为零时出力参数应满足：

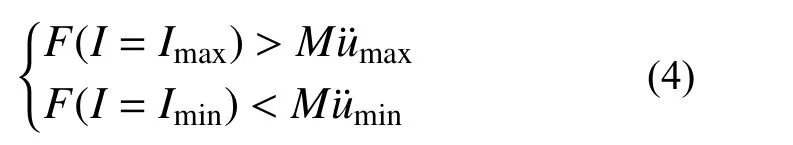
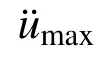
1.3 振动输入频率在线检测方法

本文所提出的on-off半主动控制方法实现的关键在于对输入频率的快速检测。然而，频率特征反映的是一段时间的数据特征，无法实时分析。本节提出一种设置时间窗口进行快速傅里叶变换(FFT)分析从而在线检测输入主频率(FFT强度最大值所对应频率)的方法，如图3所示。

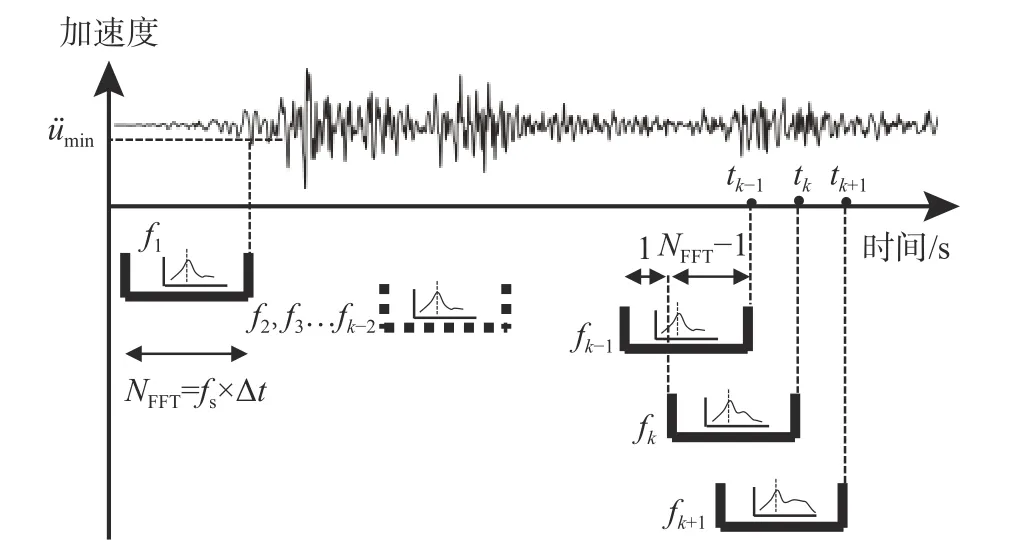
图 3 频率在线检测Fig.3 Online frequency detection

一个时间窗口Δt时间内采集数据点数NFFT为：

式中，fs为采样频率。频率检测分辨率为：

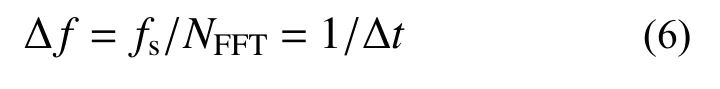
由式(6)可知，分辨率与时间窗口长度成反比。因此，时间窗口长度Δt不宜过短。例如，Δt=0.5 s，则频率分辨率Δf只有2 Hz。此时计算主频与真实主频误差可能较大，难以检测长周期输入振动的主频率。另一方面，由窗口检测所得的频率并非实时频率，而是使用了检测时间点之前Δt时间内的数据所获得的频率。因此，测得的频率反馈了历史输入的频率信息。当为提高频率检测分辨率而增加Δt时，可能导致结果与当前频率出现较大误差。因此，为了兼顾频率信息的实时性，Δt不能过长。

2 半主动控制三维隔振楼板系统试验研究

试验在天津大学滨海土木工程结构与安全教育部重点实验室进行。

2.1 磁流变阻尼器力学性能

采用LORD公司RD8041-1型磁流变阻尼器进行半主动控制。振动台试验之前使用MTS试验机进行测试。图4给出了阻尼器在2 Hz，0.015 m正弦波振动以及不同输入电流情况下的性能曲线。阻尼器出力F(N)使用Bingham模型描述如下：

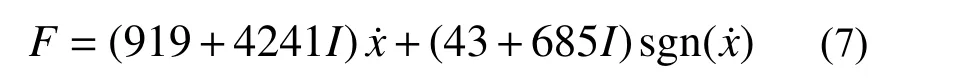
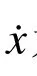
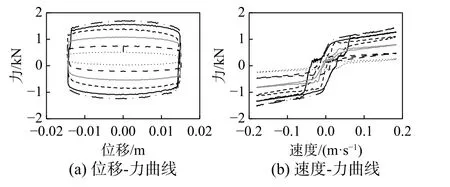
图 4 磁流变阻尼器性能曲线Fig.4 Performance curve of magnetorheological damper

2.2 振动台试验模型设计

半主动控制隔振楼板系统原型楼板尺寸为6 m×4 m，总质量约为5.3 t，使用双层型钢作为楼板龙骨，四角点支撑时一阶竖向振动频率为23.7 Hz。实际中，楼板受到的振动强度一般较小，通常加速度幅值范围为0.01 m/s2～0.5 m/s2。楼板每个方向配置4只磁流变阻尼器，可以确保结构在承受0.5 m/s2加速度时磁流变阻尼器出力可以锁定楼板。磁流变阻尼器出力可以锁定楼板。

试验时，由于振动台尺寸小于实际楼板尺寸，无法开展原型试验。而为了维持系统稳定，试验中竖向阻尼器数量至少需要4只，即与原型数量相同。由于原型结构中配置的阻尼器出力较小，较难严格按照缩尺比例配置阻尼器。另外，液压振动台运行时存在较大的背景噪音振动，一般情况下可达0.1 m/s2。因此，较难使用振动台直接准确模拟0.01 m/s2～0.5 m/s2范围的振动输入。为了验证所提出控制方法的有效性，振动台试验时兼顾振动台性能及试验目的，保证半主动控制三维隔振楼板系统的基本动力特性以及相匹配的半主动控制能力。试验中半主动控制隔振楼板系统试验模型主要由钢筋混凝土板、钢支座、钢弹簧与磁流变阻尼器组成。设计隔振系统周期与阻尼器配置与原型结构相同，在此基础上选择振动台加载幅值，确保试验时阻尼器位移不超过限值，钢弹簧、混凝土板以及钢支座等保持弹性。根据选定的加载幅值，确定楼板重量，以确保阻尼器的出力与楼板惯性力的比例与实际情况相近。

混凝土与钢材强度等级分别为C40与Q355。磁流变阻尼器与钢弹簧动力性能分别见2.1节与2.4节。表1给出了试验模型参数总结，图5给出了振动台试验现场布置图，图6给出了阻尼器与弹簧分布位置。钢筋混凝土板尺寸为1.77 m×1.0 m×0.2 m。楼板尺寸非从原型严格缩尺。根据前述方法，楼板模型的主要控制指标为重量，以确保阻尼器的出力与楼板惯性力的比例与实际情况相近。试验模型竖向尺寸为0.83 m (包括支座)。钢弹簧与阻尼器一端与锚固在振动台上的钢支座连接，另一端与钢筋混凝土板连接。钢弹簧数量共10个，均竖向放置，两端采用端板连接。磁流变阻尼器在Y(水平)向与Z(竖直)向分别布置4个，两端使用单向铰连接，试验在Y方向与Z方向进行。阻尼器采用自制压控恒流源模块供电，如图5(c)所示。采用dSPACE公司DS1104型控制器建立半主动控制系统。

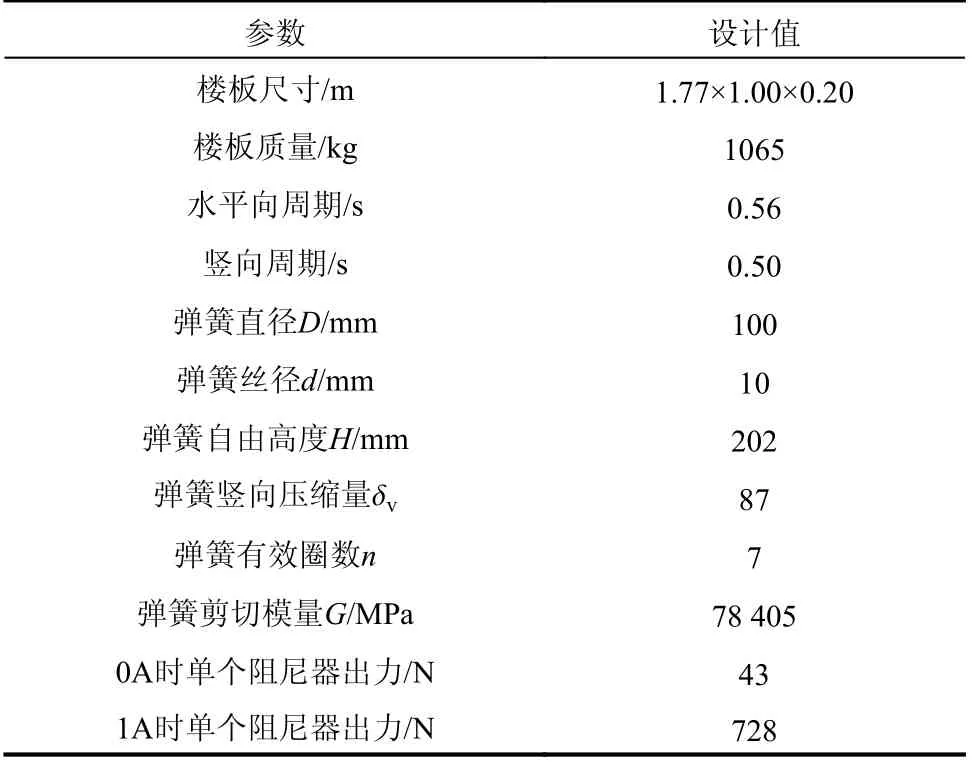
表 1 试验设计模型参数总结Table 1 Summary of the designed test model parameters

图6同时给出了测量试验模型响应所使用的加速度计(2只)与激光位移计(4只)的布置。用于半主动控制用加速度计(2只)则直接布置于振动台台面。传感器均布置于Y向与Z向。

由于阻尼器与楼板的设计未严格按照比例缩尺[17]，其误差对试验结果的影响包括：

1)与原型相比，试验中阻尼器配置相同而楼板重量降低，使得楼板在运动时等效阻尼比提高。其对于共振区(高阻尼出力模式，原型与试验均处于锁定状态)的控制效果理论上并无区别；共振区外(低阻尼出力模式)，试验中较大的阻尼理论上降低了隔振效果，试验结果偏保守。

图 5 振动台试验现场布置图Fig.5 Shaking table test setup

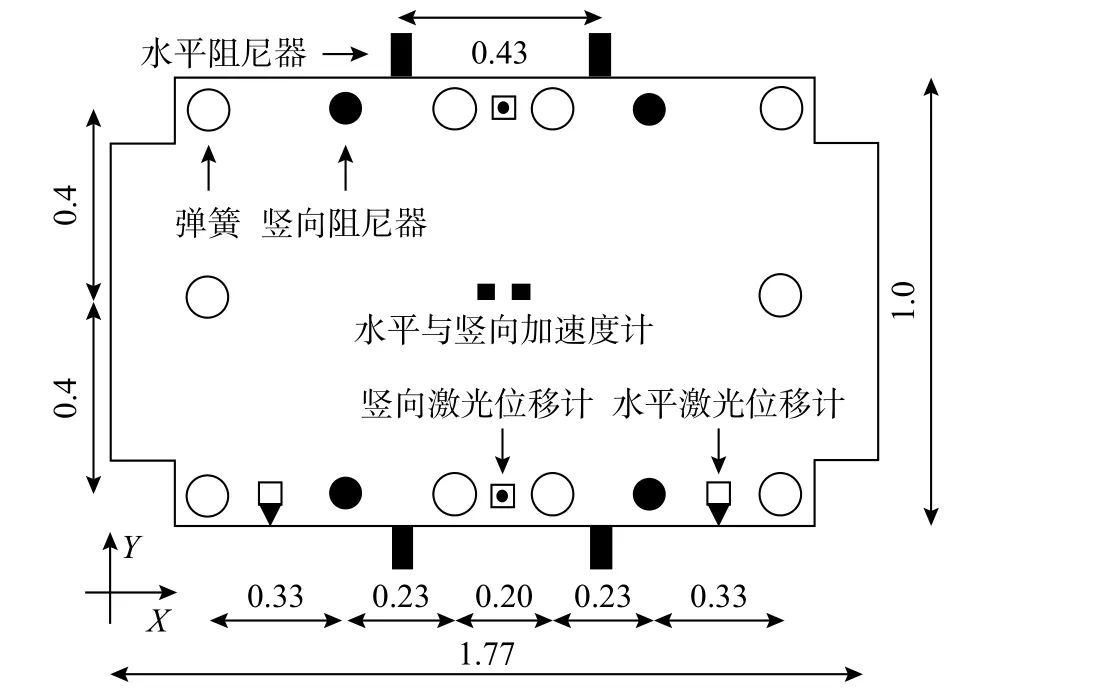
图 6 三维隔振组件与测试传感器布置 /m Fig.6 Location of 3D isolation components and sensors

2)试验中由于楼板厚度与水平尺寸的比例相对较大，使得其自身竖向振动频率高于原型楼板的第一阶频率(23.7 Hz)。考虑到本试验研究中振动频率范围主要处于20 Hz范围以内，楼板自身的模态振动模拟误差带来影响较小。

2.3 振动台试验工况与输入

振动台输入包括正弦波时程以及地震动所引起的振动时程。正弦波加载时，加载频率0.3 Hz～10 Hz。由于楼板惯性力需要克服磁流变阻尼器速度为零时的最小出力，且不可以突破阻尼器速度为零时的最大出力，根据式(4)确定加载幅值范围为0.16 m/s2～2.7 m/s2。为避免隔振层位移过大破坏阻尼器，正弦波加载时加载幅值取1 m/s2。试验加载方向分别为Y向、Z向、YZ向加载三种情况。在控制程序中设置采样频率为128 Hz，采样点数NFFT分别取256个(2 s)、512个(4 s)、1024个(8 s)。

地震动所引起的振动加载试验所需输入来自于天津大学大型地震模拟研究设施的振动台基础振动初步模拟结果。模拟分别采用ChiChi、Taft、Tianjin以及El Centro四条地震动进行加载，获得了振动台基础周围土体的振动时程曲线。同时，利用所获得的振动时程，开展了振动台外100 m左右处一座5层钢筋混凝土框架结构的数值模拟，获得了各层楼板的振动时程。振动台试验时，使用了框架结构处地面、3层楼板与5层楼板振动作为振动台输入。这些输入下文统称为振动波。试验在YZ向同时加载，共开展了6种工况的试验。工况1：输入加速度幅值1 m/s2，NFFT取512个；工况2：输入加速度幅值2 m/s2，NFFT取512个；工况3：输入加速度幅值1 m/s2，NFFT取256个；工况4：输入加速度幅值2 m/s2，NFFT取256个；工况5：输入加速度幅值1 m/s2，NFFT取1024个；工况6：输入加速度幅值2 m/s2，NFFT取1024个。图7与图8分别给出了振动台Y向与Z向输入的地面与5层振动波加速度傅里叶变换数据，输入加速度幅值2 m/s2。图7与图8中竖向虚线处频率为传递函数为1时所对应的频率，虚线左侧为共振区域。根据式(3)，当输入频率位于此区域时使用高阻尼力模式，当输入频率位于虚线右侧时使用低阻尼力模式。

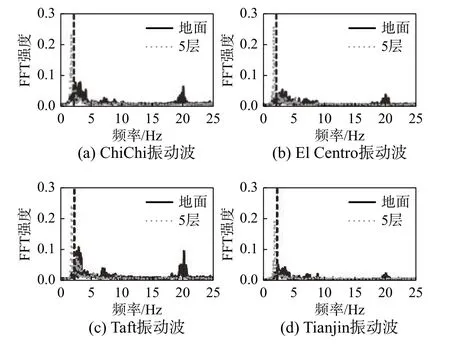
图 7 振动台试验Y向加载振动波傅里叶谱Fig.7 FFT spectra of the Y direction vibration in the shaking table test

2.4 振动台试验结果分析

2.4.1 试验现象描述

由于振动试验输入幅值较低，所用材料均保持弹性，试验中未发生混凝土板与钢支座塑性破坏等现象。在低阻尼出力模式时，楼板在Y向与Z向均表现为单自由度体系振动，未发生转动与摇摆现象。高阻尼出力模式时，楼板被锁定并与振动台同步运动。弹簧保持弹性变形，无失稳等现象。图9(a)与图9(b)分别给出了在ChiChi地面振动波加载时两竖向激光位移计的位移时程(Z1、Z2)以及ChiChi5层振动波加载时两水平向激光位移计的位移时程(Z3、Z4)。ChiChi地面振动波加载时竖向主要采用低阻尼出力模式，楼板被隔振产生隔振层位移。ChiChi5层振动波加载时水平向主要采用高阻尼出力模式，隔板被锁定，位移接近于0。同时，由图9(a)与图9(b)可以看出，加载完成后楼板位置恢复到原位，弹簧恢复原高度。另外，试验采用磁流变阻尼器位移限值为±37 mm，加载时位移均未达到此限值。

2.4.2 半主动控制频率控制区间参数确定

试验中设计了截止频率为10 Hz的2阶低通滤波器，以过滤控制电流信号突变带来的高频信号。

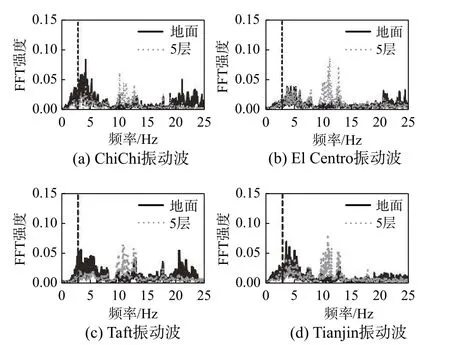
图 8 振动台试验Z向加载振动波傅里叶谱Fig.8 FFT spectra of the Z direction vibration in the shaking table test

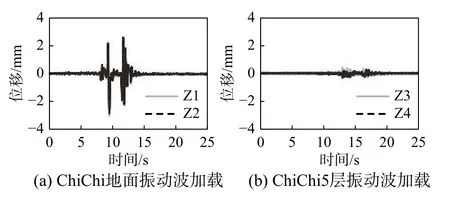
图 9 隔振层位移Fig.9 Isolation layer displacement

对Y、Z两个方向分别进行正弦波加载以确定结构的共振区间，阻尼器电流输入为0 A。通过获取振动台与楼板的振动幅值，可以计算楼板隔振的传递函数。图10给出了水平向与竖向的传递函数曲线。根据计算结果， 水平向与竖向的最大传递率分别为1.6和2.0。Z向的最大传递率高于Y向最大传递率，这主要是由于Z向的频率较高，其阻尼比较低导致。

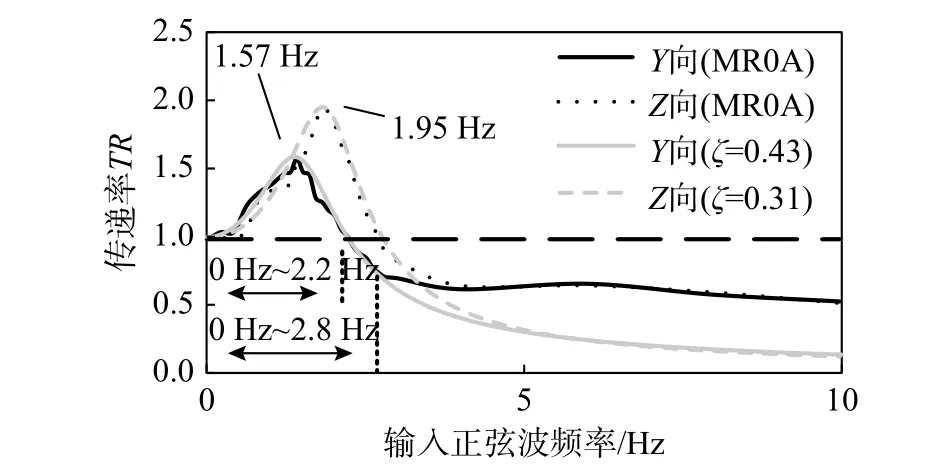
图 10 阻尼器0A电流输入时隔振系统加速度传递率Fig.10 Acceleration transmissibility for the isolation system with 0 A input for MR damper

由式(2)求导可求得传递函数TR最大值为：

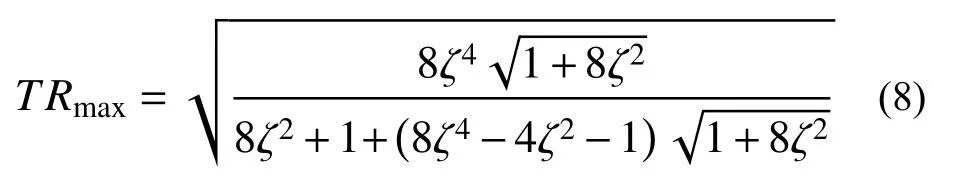
根据式(8)可以估算水平向与竖向的等效粘滞阻尼比分别为0.43、0.31。图10同时给出了使用计算所得等效粘滞阻尼比的单自由度隔振系统传递函数。由图10可知，传递率大于1的部分(共振区)，使用估算粘滞阻尼计算传递率与使用MR阻尼器传递率接近。传递率小于1部分，MR阻尼器实际等效阻尼比高于前述估算值。实际应用时，阻尼器数量减小或楼板重量增加，阻尼比降低。在不控制情况下，共振区的传递函数值将大于试验所测得结果；在共振区外，传递函数值将小于所测得结果。理论上，实际使用时半主动效果将比试验时高。

根据计算结果，水平向与竖向传递率最大值所对应的频率分别为1.57 Hz与1.95 Hz，比设计值1.79 Hz与2 Hz (见表1)分别低13%与3%。由此可得单个弹簧的水平与竖向刚度分别为10.36 kN/m与15.99 kN/m。根据式(3)，确定阻尼器在水平向与竖向的高阻尼力模式控制范围分别为(0 Hz～2.2 Hz)与(0 Hz～2.8 Hz)。理想情况下，通过高阻尼力模式可将共振区在水平向与竖向的传递率从1.6与2.0降至1.0。

2.4.3 频率在线检测结果分析

图11(a)与图11(b)分别给出了0.8 Hz与2.2 Hz两种频率Y向正弦波加载时的频率检测结果。当采集数据点数NFFT为256、512与1024时，对于0.8 Hz加载的测试结果分别为1.0 Hz，0.75 Hz与0.75 Hz；对于2.2 Hz加载的测试结果分别为2.0 Hz，2.25 Hz与2.25 Hz。三种不同的设置均可以有效检测输入振动的频率。相对来说，采集数据点数NFFT为512与1024时频率检测精度高于NFFT为256时，误差均小于10%；但采集数据点数NFFT为1024时，FFT数据窗口长度达到8 s。在频率特性复杂时，可能由于过长的窗口长度所记录的历史数据影响实时频率的准确判断。

图11(c)与图11(d)分别给出了ChiChi 5层振动波YZ向输入时Y向与Z向的频率检测结果，输入加速度幅值2 m/s2。由图11(c)与图11(d)可以看出，当采样点数越少时，所测得的频率变化相对频繁。在Y向，NFFT为512与1024时，检测频率稳定于1.75 Hz；而NFFT为256时，所测得的频率在1.5与2.0 Hz两值之间波动。在Z向，频率相对较高且在1.75 Hz～10.75 Hz随时间变动。相对来说，采集数据点数NFFT为512与1024时Y向与Z向所测得主频率信息更加符合图7与图8的线下时程分析结果。

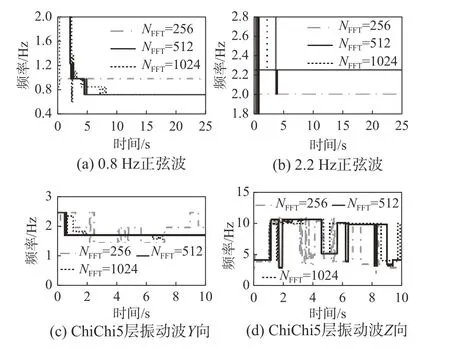
图 11 频率在线检测结果Fig.11 Results of online frequency detection

2.4.4 振动控制结果分析

图12给出了正弦波YZ向共同加载时的加速度传递率曲线。单方向加载时结果与YZ向同时加载结果接近。正弦波加载幅值为1 m/s2，加载时两个方向频率相同。on-off半主动控制在线频率检测的采集数据点数NFFT为512。结合图11可知，在共振区时，根据频率检测结果可以输出最大电流锁定楼板，使得楼板的响应接近于振动台的输入。水平Y向传递率1.08～1.11，竖直Z向传递率0.98～1.10。在共振区外，半主动控制根据检测获得频率输出最小控制电流。水平Y向最小传递率0.62，竖直Z向最小传递率0.54。

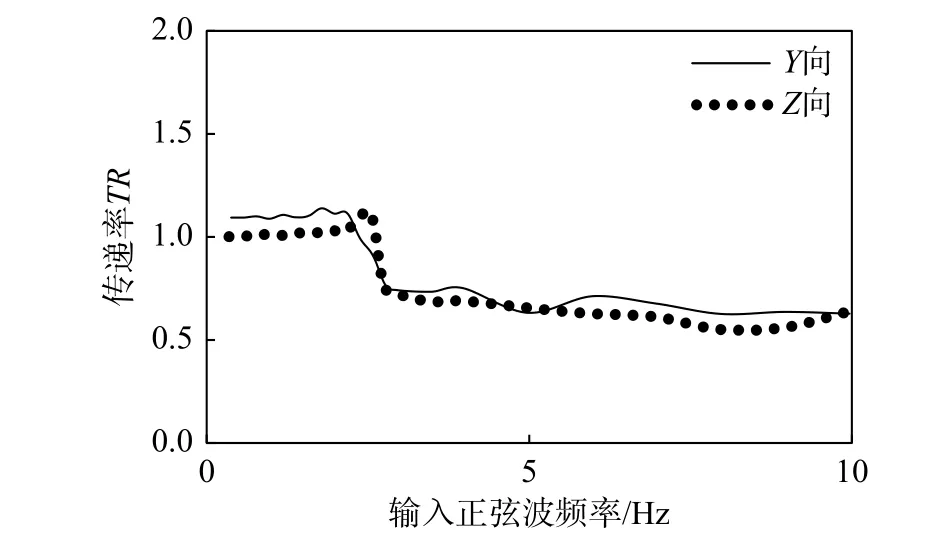
图 12 正弦输入时隔振系统加速度传递率Fig.12 Acceleration transmissibility for the isolation system under sinusoidal motion vibration

图13与图14给出了YZ向同时加载振动波时的加速度传递率统计图。从不同的采样点数对比(工况1～工况2：512；工况3～工况4：256；工况5～工况6：1024)可以看出，采样点数NFFT为512时，加速度传递率相对较小。如图14(b)所示，采样时间过长可能使得on-off控制的输出与最优控制有较大差别。因此，结合前述的频率在线检测结果，推荐使用4 s的窗口时间进行频率检测。以下主要结合采样点数NFFT为512，即FFT窗口长度为4 s的结果进行分析。

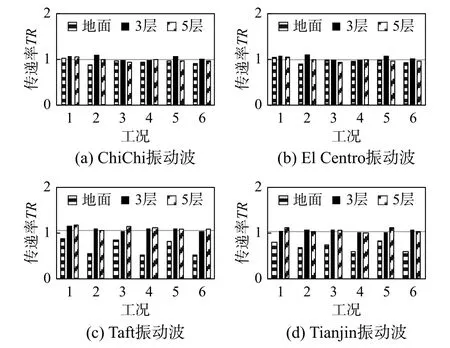
图 13 Y向加载楼板隔振加速度传递率Fig.13 Acceleration transmissibility in Y direction for the floor isolation

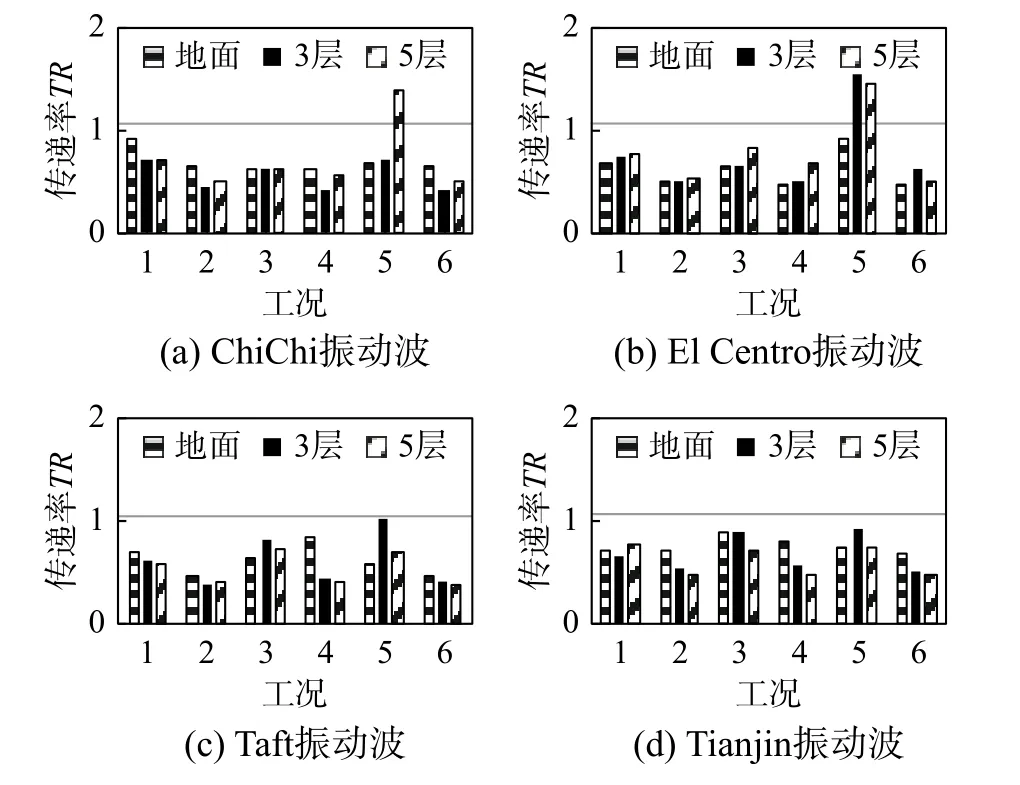
图 14 Z向加载楼板隔振加速度传递率Fig.14 Acceleration transmissibility in Z direction for the floor isolation

on-off控制结果按照阻尼器高阻尼力输出或低阻尼力输出可分为两类。当阻尼器主要以高阻尼力输出时，如Y方向输入3层与5层振动波时，楼板可以被有效锁定，加速度传递率范围为0.96～1.10。当阻尼器主要以小阻尼力输出时，on-off控制可有效降低输入幅值。Y方向加速度传递率为0.51～0.88，平均值为0.71；Z方向加速度传递率为0.38～0.86，平均值为0.58。由图8可知，Z向高频成分更为丰富，因此，其隔振控制效果更为突出。

不同的振动台输入幅值时(工况1：1 m/s2；工况2：2 m/s2)加速度传递率不同。如在ChiChi地面振动波情况下，1 m/s2加载幅值时传递率0.97，结构几乎锁定；而在2 m/s2加载幅值时传递率0.62。在传递率低于1的情况中(说明此时输入频率较高，使用了低阻尼出力模式进行控制)，不同振动波时工况1的传递率均值为0.73，工况2的传递率均值为0.53，工况2时传递率相比工况1时降低28%。这是由于工况1时，输入加速度较小，在部分时间内阻尼器仍然处于锁定状态，降低了减振效果。因此，为了提高控制效果，实际应用中应尽量降低阻尼器的低阻尼模式的阻尼。

随着层高的变化，在相同出力模式时加速度传递率并无明显变化规律，所提出的on-off控制均可以有效识别振动输入频率进行有效控制。在Y方向，地面振动波的加速度传递率低于3层与5层振动波加速度传递率，这是由于地面振动波输入时采用了高阻尼力出力模式，而3层与5层振动波输入时采用了低阻尼力出力模式。

综合不同正弦波以及振动波的控制效果可知，本文所提出的基于在线频率检测的半主动控制三维隔振楼板系统可有效检测输入振动频率特征，在不同频率特征的输入时，有效控制楼板振动。在高频振动时发挥隔振作用，而在低频振动时防止共振效应，适用于大型振动台所引起的具有不同频率特征的振动的控制。

图15给出了on-off半主动控制与阻尼器0 A电流的被动控制对比。结果表明：on-off控制与被动控制结果类似。然而，需要指明的是，振动台不同频率特征的地震动以及正弦波加载时其频率特征并不确定，被动控制难以有效控制不同频率振动。

图 15 半主动与被动控制楼板Z向加速度传递率Fig.15 Acceleration transmissibility in Z direction for the floor isolation with semi-active control and passive control

3 结论

为降低振动台的振动对实验室以及周边建筑物的影响，建立了一种半主动控制三维隔振楼板系统，提出了半主动控制方法以及振动主频识别方法，开展了振动台试验。得到以下结论：

(1) 所提出的频率在线检测方法可有效检测输入振动波频率。FFT时间窗口的长度不同，频率检测精度不同，并不同程度地受已经过部分振动输入的影响。试验结果表明：采用4 s的窗口长度，可较准确检测本研究中所采用的正弦波与地震波所引起振动的频率。

(2) 所提出的on-off控制，当检测主频处于系统共振区时，采用高阻尼出力模式，避免系统共振；当检测主频处于系统共振区外时，采用低阻尼出力模式，降低振动响应。振动台试验结果表明：本研究中地震波试验引起的振动加载时，高阻尼出力模式下加速度传递率范围为0.96～1.11；低阻尼出力模式下加速度传递率平均值在Y方向为0.71，在Z方向为0.58。

(3) 阻尼器由于存在摩擦力，振动幅值较小时可能产生锁死现象。试验中2 m/s2幅值振动加载时比1 m/s2幅值时传递率提高28%。为提高控制效果，实际应用时应降低阻尼器低阻尼力模式时的阻尼。