岩体质量可变模糊集评价模型研究及其应用

吴 峰

（广东省冶金建筑设计研究院有限公司）

对地下矿山来说，岩体质量评估是一项系统且基础性的工作。岩体质量分级影响因素较多，且因素之间关系复杂，目前岩体质量评估主要采用传统的RMR分类法［1］、Q分类法［2］、BQ分类法［3］或者基于数学理论构建评价模型，如神经网络［4］、云模型［5］等，但上述每种方法都有各自的适应条件和局限性。由于岩体质量评估具有随机性和模糊性特点，常规的数学模型评估结果可能存在与实际情况不符。可变模糊集理论是在工程模糊集理论的基础上提出的用于处理具有模糊性问题的理论模型，为不确定问题的处理提供了理论遵循，作为一种多指标综合评价模型，在岩爆、溃坝、突水等风险识别方面能取得较为满意的评估结果［6］，而在岩体质量评估方面应用较少。鉴于此，本研究采用改进层次分析法计算指标权重，构建基于改进层次分析法—可变模糊集的岩体质量综合评估模型，以提高岩体质量评估精度。

1 改进层次分析法—可变模糊集综合评价模型

为提高随机性和模糊性问题评估的精度，将改进层次分析法和可变模糊集理论耦合构建综合评价指标模型，具体实现过程：①构建综合评价指标体系，基于改进层次分析法确定指标权重；②通过可变模糊集理论确定待评对象相对隶属度，将相对隶属度与指标权重相乘，得到综合隶属度；③根据综合隶属度计算结果，基于判定准则，确定评估等级。

1.1 改进层次分析法指标权重确定

权重直接决定了评估结果的合理性。层次分析法是以九标度理论为基础构建指标比较矩阵，需要多次调整判断矩阵以满足一致性要求，计算相对复杂。基于三标度理论的改进层次分析法确定指标权重，只需要进行指标两两之间重要性比较，对评估者主观认知要求较低，权重计算更具客观性，评估结果更可靠［7］。

1.1.1 比较矩阵建立

基于三标度理论建立指标比较矩阵A：

其中，aij取值如下。

1.1.2 最优传递矩阵建立

最优传递矩阵R为

式中，din=exp(rin)。

1.1.3 主观权值计算

采用乘积方根法来确定主观权值，具体计算过程如下。

1.2 可变模糊集

1.2.1 可变模糊集理论

陈守煜以工程模糊集理论创建了可变模糊集理论，通过计算相对隶属度和综合隶属度，基于判定准则，确定最终评估结果，为解决模糊性问题提供了思路，可变模糊集理论原理及具体计算步骤见文献［8］。

如图1所示，根据可变模糊理论的定义，X=［a，b］为实轴上可变模糊集合V的吸引域，X1=［c，d］为包含X的可变集合范围域，其中［c，a］和［b，d］为排斥域，M为中值点。假设x为X中任意区间内的量值，根据其在实轴上相对于M的位置关系确定相对差异函数，其中，相对差异函数计算公式如下。

当x位于M左侧区间时，

当x位于M右侧区间时，

式中，a，b，c，d分别表示某指标等级吸引域和排斥域取值，M为中值，一般地，对于边界等级取边界限值（如本研究将岩体质量划分为5级，Ⅰ级和Ⅴ级为边界分级，此时M取边界限值），非边界等级取等级划分区间中值。

1.2.2 计算过程

（1）根据指标分级情况，构建标准区间矩阵Iab：

式中，a、b分别为指标等级划分标准的上限和下限。如岩体质量评价中指标RQD，其分级标准中Ⅰ级取值为［90~100］，则a，b分别等于100、90。

（2）构建变动区间矩阵Icd，表示为

式中，h代表等级划分个数，c、d分别代表变动区间上下限值，即排斥域取值。

（3）计算单指标隶属度函数，单指标隶属度函数表示为

式中，e，f为模型优化参数，一般取e=1，2；f=1，2。

（4）根据单指标隶属度度，可以确定综合隶属度，计算公式为

风险等级划分标准见表1。

?

2 模型应用

2.1 构建综合评价指标体系

建立科学的综合评价指标体系是开展质量评估的前提与基础。在参考文献和考虑了现场实际情况下，决定选取RQD（X1）、岩石单轴饱和抗压强度（X2）、岩石完整性系数Kv（X3）、结构面强度系数Jf（X4）、地下水渗水量w（X5）等5个指标构建地下矿山岩体质量综合评价指标体系。将岩体质量划分5个等级，即Ⅰ~Ⅴ级，其中Ⅰ级和Ⅴ级分别代表岩体质量最好和最差。具体指标等级划分标准见表2。

以三山岛金矿新立矿区-200 m中段岩体为研究对象进行岩体质量评估。该矿区属破碎带蚀变岩型特大型金矿床，地质条件复杂，围岩质量变化较大。矿石回采过程中，在爆破振动、地质构造、地下水等综合作用下，常伴有浮石掉落、冒顶和塌方等灾害，严重威胁着工人作业安全性。基于现场实测和翻阅地质资料［9］，汇总各指标参数取值见表2。

2.2 指标权重计算

根据文献［6］，构建比较矩阵为

指标权重计算结果

2.3 可变模糊集计算过程

（1）根据表1和式（8），得到标准区间矩阵Iab：

（2）根据式（9），构建变动区间矩阵Icd：

（3）构建中值点矩阵M：

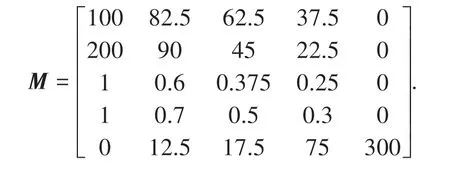
（4）根据式（10），建立相对隶属度函数为

（5）根据式（11）~式（12），可以获得相对隶属度和综合隶属度，为进一步验证本文所建立的基于改进层次分析法—可变模糊集的适用性，将云模型和未确知测度结果相对比，评估结果见表3。

根据表3可知，三山岛金矿新立矿区-200 m中段岩体质量综合隶属度为3.406，根据表1风险等级划分标准可知，该岩体质量等级为Ⅲ级。经过现场调研发现，该中段岩体呈块体化或者散体结构破碎，岩体极易沿结构面滑落，岩体稳定性属于中等—不稳定，锚网喷联合支护后，岩体破坏得以控制，冒落等灾害现象减少，作业安全性进一步提高，本研究所建立的评价模型评估结果与现场实际情况相符合。通过与云模型和未确知测度两种计算模型评估结果对比发现，3种评价模型评估结果一致，表明基于改进层次分析法—可变模糊集的综合评估模型在岩体质量评估方面具有适用性，可以为地下工程岩体质量评估工作提供理论依据。

3 结论

（1）为提高指标权重计算合理性，基于三标度理论对传统层次分析法进行改进，指标权重计算结果更具客观性，能提高评估结果的可靠性和准确性。

（2）考虑地下工程岩体质量评估具有随机性和模糊性特点，引入可变模糊集理论构建岩体质量评价模型，对三山岛金矿新立矿区岩体质量进行评价，研究结果表明，该模型评估结果与实际情况相符，与其他模型计算结果一致，可以为岩体质量评估工作提供理论依据。

（3）由于岩体质量评估影响因素较多，且因素之间关系复杂，接下来还需进一步完善评价指标体系，以提高模型的适用性和应用价值。