二次函数的应用

冯利卿

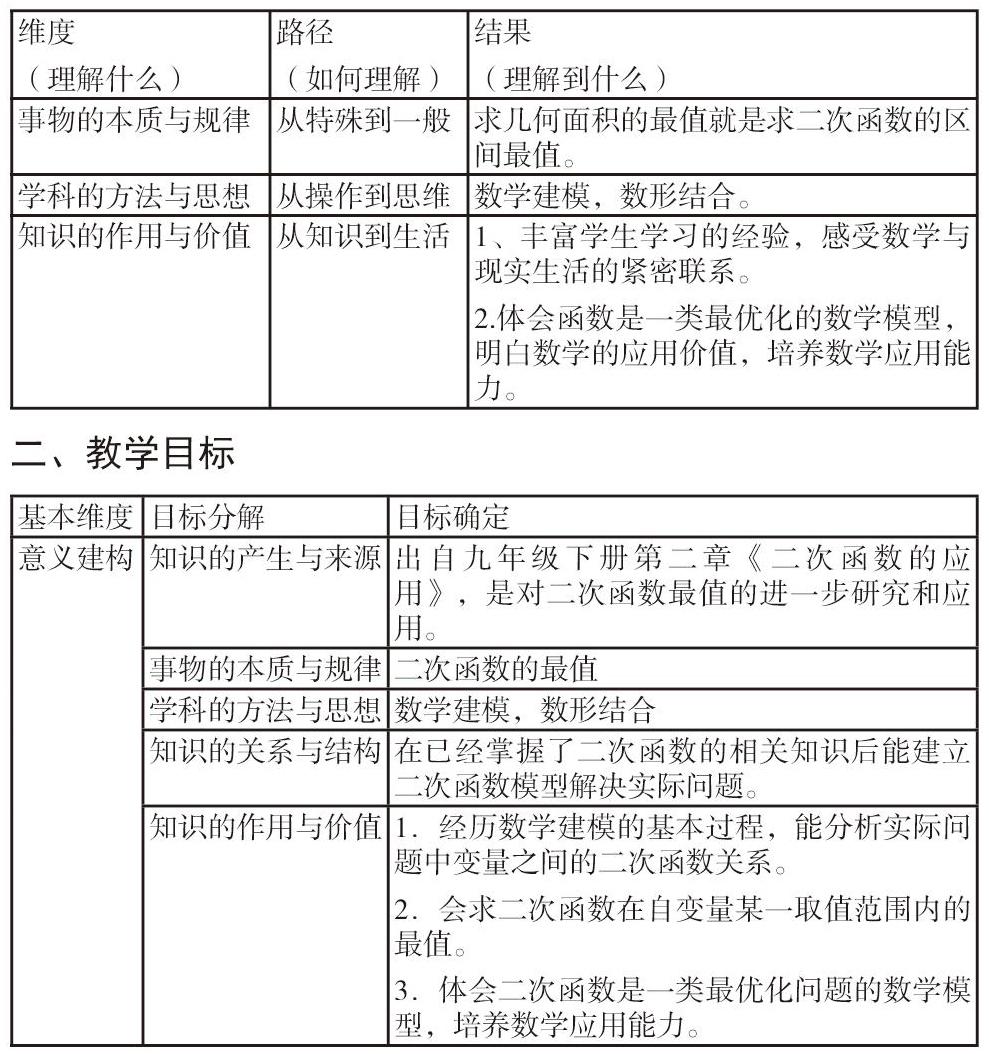
一、教材及学情分析

1.学情分析

学生已经掌握了二次函数的概念，图像以及性质等，并能熟练的将二次函数的一般式转化为顶点式。并且学生对如何求解二次函数的最值有了一定的思考方向，能画出二次函数的简图。并具有一定的运用函数模型解决实际问题的经验。

共鸣处：在生活实践中，人们常常遇到带有“最”字的问题，如在一定的方案中，消耗最低，利润最大等。这些最值问题常常可以用函数模型来刻画，转化成求二次函数的最值。

困难处：如何将实际问题转化成函数模型？如何确定实际背景下的自變量的取值范围？如何在自变量的取值范围下求出最值？

2.教材分析

二、教学目标

三、教学重难点

重点：能够表示不同背景下变量之间的二次函数关系，掌握求解几何面积最值的基本步骤。

难点：1、能够表示不同背景下实际问题中变量之间的二次函数关系;

2、对函数图象的顶点，端点与最值关系的理解与应用。

四、教学设计