一种改进的FEEMD-FOA-LSSVM短期风速预测方案
李敏洁,高桂革,曾宪文
(1. 上海电机学院电气学院,上海 201306;2. 上海电机学院电电子信息学院,上海 201306)
0 引言
风力发电作为一种发展迅速的可再生能源发电,近些年在全球范围内装机量越来越多,风力发电在电网系统中所占的比例也越来越高,然而风速的非平稳性对电力系统的稳定和经济运行造成了很大的障碍[1]。提高风电场的风速预测精度,进而可以降低风力发电对电力系统的影响。
国内外学者在对风速预测方法的研究中发现,风速序列的非平稳性会对模型的预测结果产生严重影响,对于该问题的解决方法主要有:小波变换[2],经验模态分解[3]等,经验模态分解算法(EMD)是在时频域对信号进行处理的方法,该方法不需要对信号进行提前的分析,可以直接对未知的信号进行分解,自适应能高,但使用该分解方法时存在频率混叠问题,并且在进行包络线的求解时出现端点效应。而基于噪声辅助分析的集合经验模态分解算[4](EEMD)虽然可以处理分解过程中的频率混叠问题,改善经验模态分解的不足,但是需要耗费较长时间计算,并且存在端点效应。快速集合经验模态分解(Fast ensemble empirical mode decomposition,FEEMD)是 EEMD的快速实现方式,其原理与EEMD基本相同,因此在对风速序列分解过程中计算极值点的包络线时,端点效应问题也不可忽视。文献[5]通过加余弦函数来改进 FEEMD减少端点效应的影响。通过文献[6][7]中观察使用FEEMD分解后产生的各模态分量,发现存在端点效应问题。
统计方法是风速预测中比较成熟且广泛应用的方法[8],适用于短期或超短期预测,统计方法中基于人工智能的学习方法主要有神经网络[9]、支持向量机[10]等,相较与支持向量机的优缺点,最小二乘支持向量机[11]对其缺点进行了改进,在将模型的计算复杂度大幅降低,减少模型的训练时间的同时还保留了其泛化能力强等优点。然而最小二乘支持向量机的预测效果与模型参数的选取有关,文献研究表明,对最小二乘支持向量机参数使用寻优算法进行优化,可以有效地提高模型的预测精度。
因此,文中通过改进的 FEEMD算法分解风速序列,降低风速的不稳定性,改善端点效应,利用样本熵重组分解后的序列,得到新的子序列,同时为提高 LSSVM模型预测效果对模型参数使用改进FOA算法进行优化,最后对各个新序列使用优化的 LSSVM模型进行预测,合并各预测值实现预测。
1 研究理论
1.1 快速集合经验模态分解
快速集合经验模态分解是对EEMD的改进,可以有效的降低风速序列的非平稳性,减少频率混叠的影响。通过优化停止筛分准则,减少分解的计算时间。文献[12]证明,FEEMD是EEMD的快速实现方式。步骤概括为:
Step.1将原始的风速时间序列x(t)加入白噪声nm(t)得到新的时间序列xm(t):

Step.2对新的时间序列xm(t)使用EMD分解,得到j个IMF以及一个余项。

m分解运行的次数。
Step.3重复Step.1和Step.2,至m=M。
Step.4由式(3)(4)做集成平均得到最终的本征模态函数IMFj(t)以及余项r(t)。

1.2 果蝇优化算法
果蝇优化算法(fruit fly optimization algorithm,FOA)作为一种群智能优化搜索算法[13],通过模拟果蝇觅食的行为,寻找最优解。该算法步骤总结为:
Step.1初始化种群的规模N,种群的迭代次数tmax,种群的搜索半径r及果蝇的二维坐标位置xi,yi。
Step.2果蝇个体在半径为r的范围内通过味觉搜索食物,并且通过式(5)更新果蝇的位置。
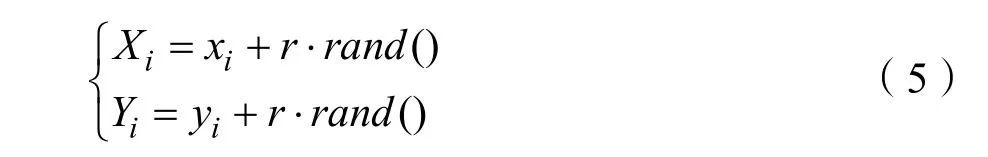
Step.3通过式(6)计算果蝇与原点的距离D,并将D的倒数S作为味道浓度的判断值。

Step.4将 S带入适应度函数,计算种群个体的味道浓度Sm:

Step.5记录种群中味道浓度值最佳的个体的位置和其浓度值(以最小值为例):
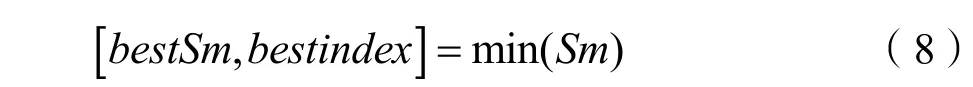
Step.6记录所得最优浓度值以及位置坐标,种群内其他果蝇通过视觉向最优位置飞去。
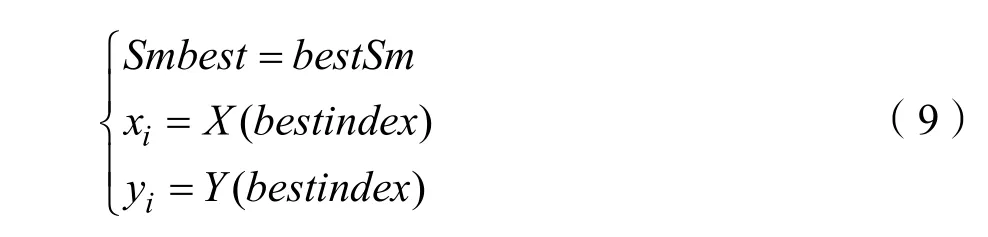
Step.7迭代寻优,至达到最大迭代次数,输出最优结果。
1.3 最小二乘支持向量机
最小二乘支持向量机(Least Squares Support Vector Machine, LSSVM)作为一种核函数学习机,在处理预测问题时,不但改善了 SVM 二次规划求解过程中收敛精度低、速度慢的问题,也保留了SVM的诸多优点,通过文献[11]可得算法最后的回归函如式(10):
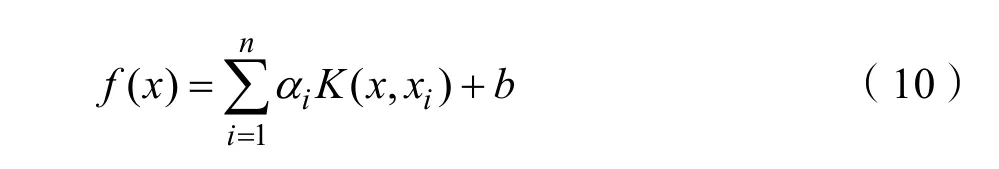
文中所提出的改进的 FEEMD-FOA-LSSVM模型所选用的核函数K(x,xi)为径向基核函数。
2 改进的 FEEMD-FOA-LSSVM模型
2.1 改进的FEEMD算法
FEEMD算法在分解过程中需要根据信号的局部极值点通过三次样条插值求解上下包络线,但是在拟合包络线时由于信号序列两侧端点处同时为极大(小)值的概率并不大,所求得的包络线时确定和不确定的结合,所以在信号序列的边界端点处会出现大幅发散问题,这种发散会随着分解次数的叠加逐渐影响信号序列内部,这种现象为端点效应[14]。
针对该问题,文中采用方法如下:
在信号规律性较强时,以信号左端点M为例,第一个极大(小)值为T,第一个极小(大)值为N,从N为起点在信号内部寻找与波形M-T-N最为相似的子波M′-T′-N′,以子波的左端开始对原信号进行延拓,延拓的部分包含原信号的一个极大值点和极小值点。右端点处同理。
在信号规律性较弱时,设风速信号的两侧端点的值分别为Xm、Xn,选取与端点Xm接近的 3个极大值点(极小值点),将Xm附近的3个极大值(极小值)的时间间隔的均值作为插入极值点的位置,计算三个点的平均值Xt,将Xt作为要插入的极值点,因此,在端点Xm处增加了一个极大值和极小值。端点Xn处同理,得到的新极值点序列为X(t)。
使用三次样条插值求取X(t)包络线。
2.2 改进果蝇算法
2.2.1 自适应搜索半径策略
标准的 FOA算法的搜索步长是由搜索半径决定的,在搜索前期需要较大的搜索范围,此时全局搜索能力强,在搜索后期,需要较小的搜索范围,此时局部搜索能力强,但标准的FOA算法在味觉搜索过程中搜索半径随机更新,随机性使得算法的收敛效果并不理想,基于此提出一种新的自适应的搜索半径的策略:
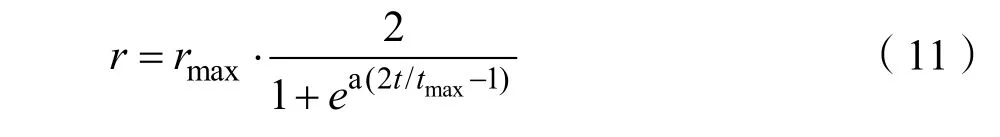
其中rmax为最大搜索半径,t为算法迭代次数,tmax为最大迭代次数,a=9。设最大半径为 100,最大运行次数为100,半径变化趋势如图1所示。
从图1可以看出,在算法迭代前期,r的取值较大,且衰减速度较慢,有利于提高全局搜索能力,避免陷入局部极值,在算法后期,r值逐渐变小,提高局部搜索,使算法更快的靠近局部最优解。因此新的搜索半径策略能更好地平衡全局搜索与局部搜索之间的关系。

图1 新的搜索半径变化图Fig.1 New search radius change graph
2.2.2 个体交叉学习策略
若在味觉搜索过程中得到的最优个体不是全局最优,算法可能会陷入局部最优,因此提出对其他差于最优解的个体采用交叉学习的策略,如式(12)
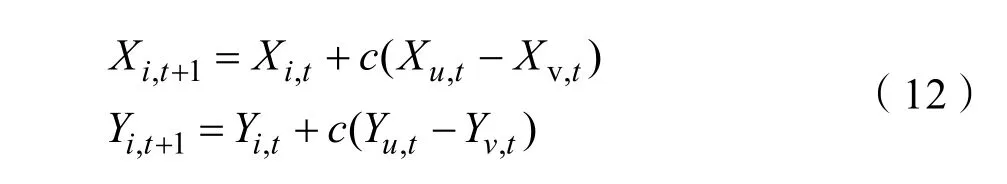
其中c∈(0,1),Xu,t,Yu,t为当前第t代中不同于i的其他个体的位置坐标。加强不同果蝇个体的相互协同,引导剩余果蝇向最优位置飞行,改变标准FOA算法的单一搜索模式,有利于算法的全局寻优。
3 模型建立
3.1 改进的FOA-LSSVM模型
LSSVM 模型的训练及预测能力的好坏主要是由核参数σ和惩罚因子γ决定的,依靠人工经验选取的方法并不完全可靠,导致预测结果并不理想,因此,文中选用改进的 FOA算法实现对LSSVM模型参数的优化,提高模型准确性。
3.2 样本熵
针对原始的风速序列使用改进的 FEEMD算法进行分解后产生的子序列较多,导致预测时间增加的问题,文中引入样本熵[15]重组概念,将分解后的子序列进行样本熵计算,将熵值接近的子序列进行合并,完成模态分量的重组进而提高预测效率。
3.3 预测过程
文中的预测过程如图 2所示。使用改进的FEEMD算法对原始风速序列进行分解后,使用样本熵对分解的子序列进行重组,得到三个高中低不同频率的子序列,对新的子序列建立FOA-LSSVM预测模型,将预测结果叠加完成预测。
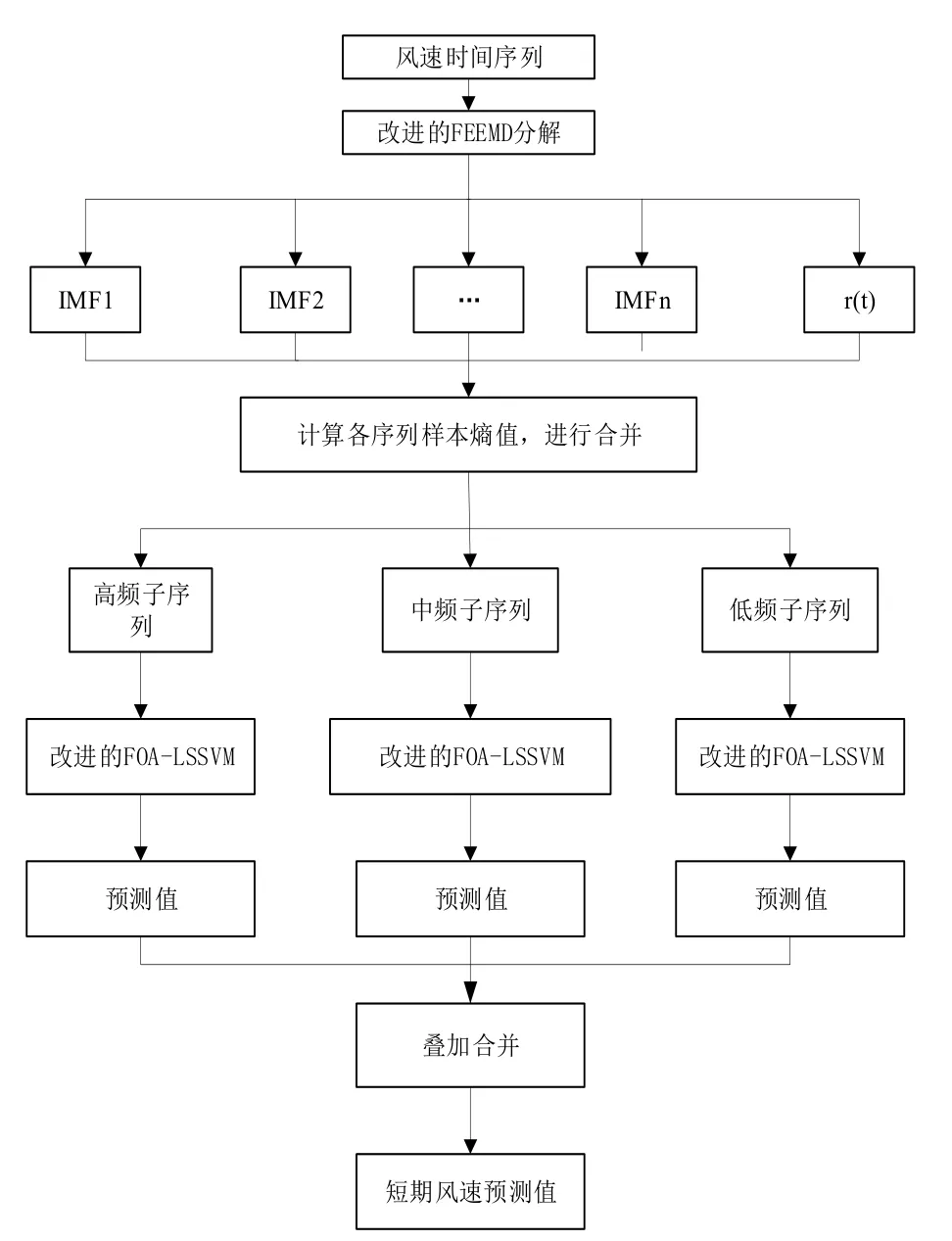
图2 预测流程图Fig.2 For ecast flow chart
4 仿真实验
4.1 改进的FEEMD算法
采用西北某风电场 15天的实际风速数据建立本文的预测模型进行仿真实验,验证本文所改进算法以及预测模型的合理性,如图3所示为实际风速序列图。
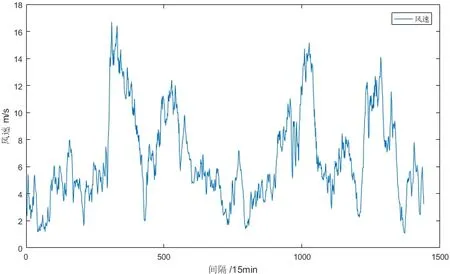
图3 风速序列图Fig.3 W ind speed sequence
由图3可以看出,采样点原始的风速的随机的,并不稳定,这种随机性、不稳定性使得直接对风速进行预测时,预测结果并不理想,因此需要对原始的风速信号进行处理以降低这种不稳定性。
图4为使用标准的FEEMD算法进行分解后的各子序列图,图5为使用改进的FEEMD算法进行分解后得到的IMF以及余项。
从图4和图5可以看出,在使用不同的分解算法后都产生了一系列相对稳定的子序列,但是在图4中,标准的FEEMD算法分解后,在IMF2、IMF3、IMF4、IMF5、IMF7的起点以及各序列的终点处,都存在端点发散的现象,即端点效应。使用改进的FEEMD算法进行分解并对比图4可以看出,分解后得到的各子序列在两侧端点没有大幅摆动现象,端点问题明显得到了改善。
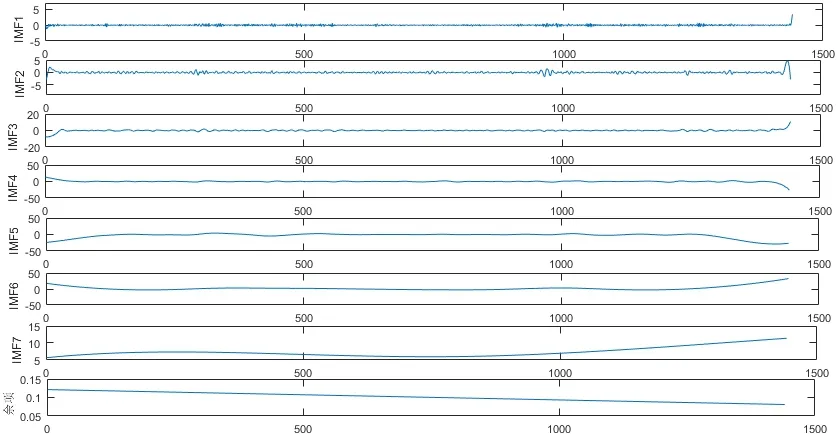
图4 标准FEEMD算法分解图Fig.4 Standard FEEMD algorithm decomposition
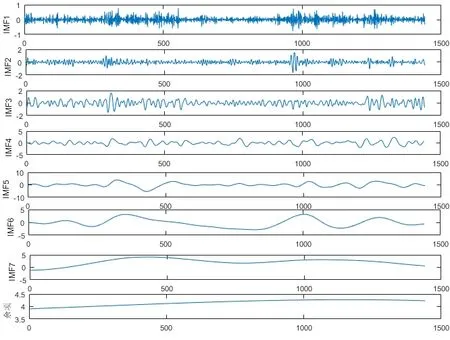
图5 改进FEEMD算法分解图Fig.5 Improved FEMED algorithm decomposition
4.2 改进的FOA优化算法
文中通过改进的FOA算法对LSSVM模型的参数进行优化。为证明所改进的FOA算法的优越性,选用基本测试函数中的单峰测试函数Sphere函数和多峰测试函数 Schaffer函数进行仿真测试,两种函数的最小值均为 0,函数表达式如式(13)(14):
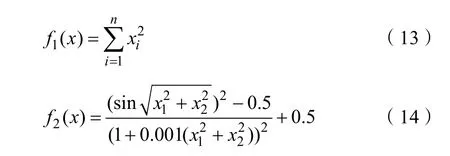
分别使用标准的FOA算法,改进的FOA算法以及标准的粒子群算法分别对上述测试函数进行最小值寻优,算法各迭代150次,将测试结果平均值以及标准偏差进行对比分析,结果如图 6及表1所示。
从图6中可以看出,改进的FOA算法相比于标准的FOA算法以及PSO算法具有更快的收敛速度,而表1中数据显示,改进的FOA算法的均值和标准差小于其他两种算法,说明改进的FOA算法的稳定性以及求解精度更高。因此,文中所改进的 FOA算法在寻找函数的最优解时具有优越性。
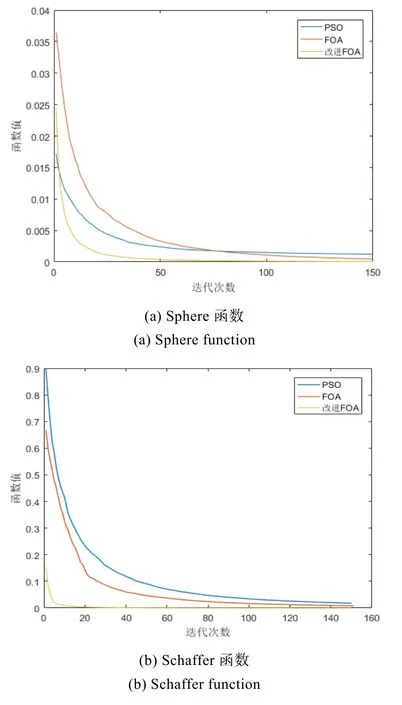
图6 不同测试函数的收敛曲线Fig.6 Convergence curves of different test functions
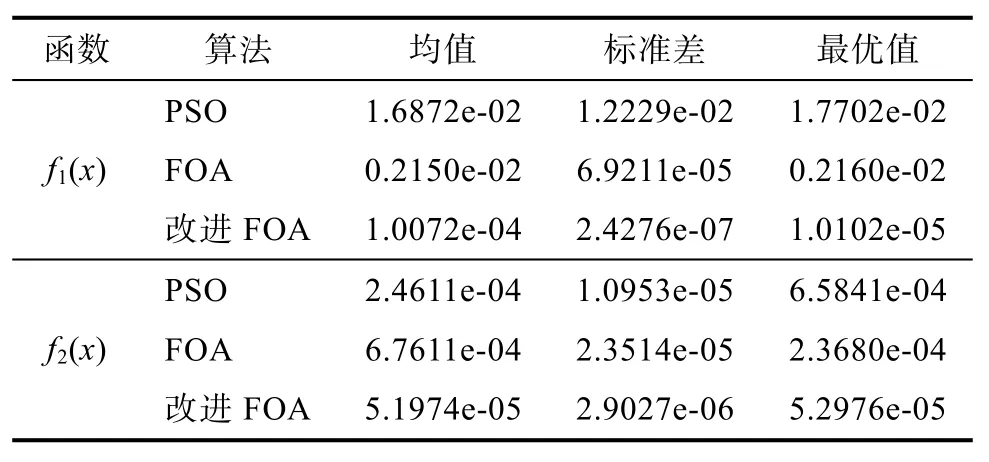
表1 三种算法性能对比Tab.1 Performan ce comparison of three algorithms
4.3 案例仿真
对在4.1中IMF1~IMF7以及余项进行样本熵计算,得到各个模态分量的熵值。

表2 各序列熵值Tab.2 Entropy of each sequence
根据得到的计算结果进行样本熵重组,将IMF1~IMF3进行合并,IMF4、IMF5进行合并,剩余项进行合并。图7为进行样本熵重组后得到三个不同频率的新子序列,对高中低新子序列分别搭建改进的FOA-LSSVM预测模型,将预测结果叠加得到预测值。
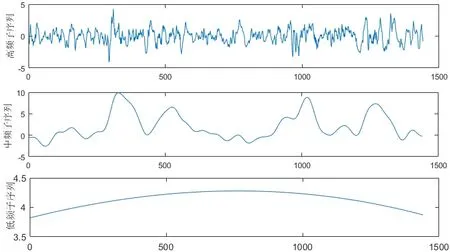
图7 根据样本熵合并后的子序列Fig.7 Subse quences combined according to sample entropy
为验证所提改进的 FEEMD-FOA-LSSVM 模型的优越性,选择标准的LSSVM模型,FEEMDLSSVM模型以及FEEMD-FOA-LSSVM模型分别预测未来一天的风速,所得预测曲线如图8所示。
为了对预测结果进行进一步评价,采用平均绝对百分比误差(MAPE),平均绝对误差(MAE),均方根误差(RMSE)三个评价指标对预测结果分析。数学表达式如式(15)~(17):
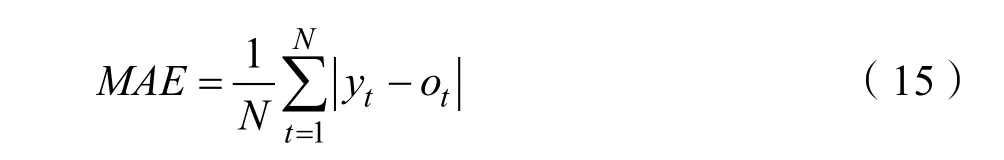

式中,yt为实际风速,ot为预测风速,N为样本预测个数。
从表3以及图8可以看出,未对原始数据进行分解直接进行预测的 LSSVM模型的预测效果并不理想,并且预测误差相对较高。分别使用改进的FEEMD算法以及改进的FOA算法进行优化后,预测结果曲线与原始风速曲线相对更为接近,预测误差有所降低,说明使用改进的 FEEMD算法对原始风速数据进行改进以后能降低风速序列不稳定性带来的影响。改进的FOA-LSSVM模型预测精度的提高说明使用优化算法能有效的改善模型的预测精度。因此,通过对比分析文中所提的改进的 FEEMD-FOA-LSSVM 模型预测结果与原始风速曲线最为接近且预测误差最低,说明该模型具有可行性。
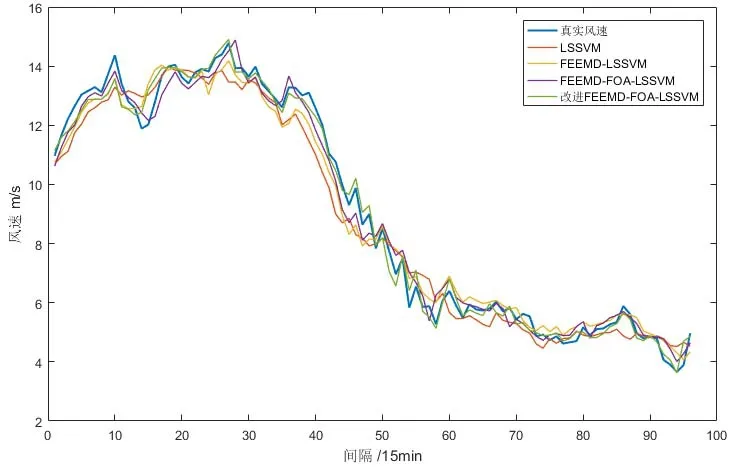
图8 模型各预测结果Fig.8 Model prediction results
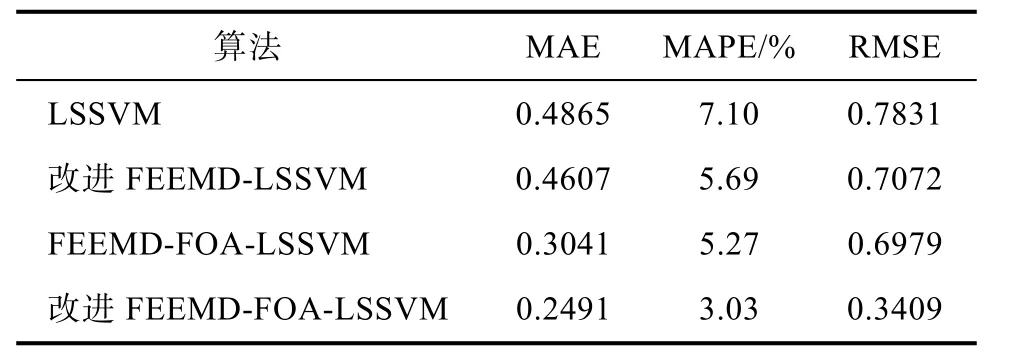
表3 预测模型误差对比Tab.3 Comparison of prediction model errors
5 结论
文中对某风电场的原始风速序列使用改进的FEEMD-FOA-LSSVM模型进行分解后重组预测,并对未来一天风速进行预测分析,得到结论如下:
(1)相比于传统的 EEMD算法,改进的FEEMD算法在保持快速分解的同时降低了端点效应带来的影响,改善了风速序列的不稳定性。
(2)对于FOA算法局部搜索能力强而全局搜索能力差的缺点,自适应搜索半径策略能很好地协调全局搜索与局部搜索关系,个体交叉学习的策略增加最优解的搜索模式,避免搜索陷入局部最优。使用改进的FOA算法对LSSVM模型参数进行优化寻优,相比于标准的FOA算法,预测精度得到提高。
通过仿真实验与其他模型对比分析,文中所提改进 FEEMD-FOA-LSSVM模型能实现更好的预测效果。

