基于时变时滞的电力系统稳定性分析
沈 力,张云佐
(1. 江苏省城市规划设计研究院,江苏 南京 210036;2. 石家庄铁道大学 信息科学与技术学院,河北 石家庄 050043)
0 引言
随着电网智能化地发展,现代电力系统越来越趋向于多互联,大规模方向发展,所以仅仅依靠传统的区域信号控制方法可能满足不了系统对性能的要求。近30年来,随着现代电力通信中向量测量单元技术的广泛应用,使得将本地电力系统信息同步采样并传送至远程控制中心成为可能。各种广域控制信道在电力信息的传输过程中难免会存在时滞且随时间变化的,这类时滞的存在将会直接破坏电力系统的稳定性。因此,研究分析含时变时滞电力系统稳定性问题具有实际意义。
近些年,对于含有时滞的电力系统,国内外学者的研究方法大都是基于 Lyapunov直接法的时域法[1-6]。通过构建Lyapunov-Krasovskii泛函,借助Lyapunov稳定理论分析系统的稳定性,给出稳定判据,最后利用线性矩阵不等式工具箱求解得到时滞电力系统的稳定裕度。文献[7]提出并将自由权矩阵的分析方法引入时滞系统鲁棒控制的研究中,在一定程度上克服了先前分析方法的局限性。文献[8]将Wirtinger不等式作为一种特例,提出一种新的积分不等式处理泛函导数中的积分项,给出了时滞离散系统的稳定判据。文献[9]利用系统状态中的二重积分项,给出一种将Wirtinger不等式包含在内的的新的积分不等式。文献[10]在Jensen不等式的基础上,提出一种含Jensen不等式的新的积分不等式,具有更小的保守性。文献[11]避开讨论Wirtinger不等式,进一步讨论了无穷形式的积分不等式,同时给出了时滞二次型的处理方法,有助于处理文章泛函导数中时滞二次项。文献[12]考虑系统时滞变化率,介绍了一种逆凸不等式,提出了一种新的增广形式的Lyapunov-Krasovskii泛函,虽然很大程度上降低了时滞系统现有结果的保守性,但是,在实际电力系统中时滞变化率是很难测量的,文章通过构建一种新的增广Lyapunov-Krasovskii泛函,合理地避开了时滞变化率的讨论。文献[13]将文献[8]的方法应用到单机无穷大电力系统中。文献[14]应用基于牛顿-莱布尼茨的自由权矩阵方法处理泛函导数中的积分项,给出的时滞电力系统的稳定性判据具有较大的保守性。文献[15]舍弃Jensen不等式,利用Wirtinger不等式对泛函导数中积分项进行处理,所得的时滞电力系统的稳定性判据也具有一定的局限性。
文章提出一种新的增广型Lyapunov-Krasovskii泛函作为系统的能量函数,应用逆凸不等式[12]对能量函数求导后得到的积分项进行有效地放缩,然后分析系统的Lyapunov稳定性,根据给出的稳定判据求解时滞稳定裕度。与现有文献的结果相比较,文章方法得到的稳定裕度更大一些。
文章采用如下标号:Rn和Rn×m分别表示实数域上的n维向量空间和n×m维矩阵空间;Rn×n表示n阶正对称矩阵集合;RT和R–1表示矩阵的转置和逆;I和0分别表示单位矩阵和零矩阵;P>0

1 系统模型
通常,含时变时滞系统的数学模型可化简为:
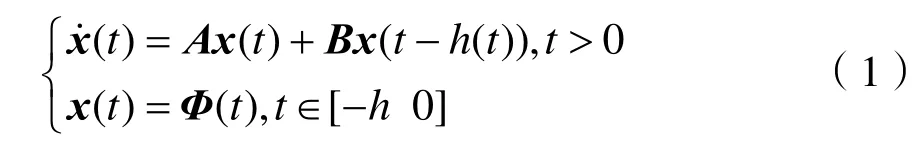
式(1)中:x(t)∈Rn,是状态向量;A、B为系统矩阵;0 为了得到系统稳定判据[10-13],给出了3个引理。 引理 1:定义可导函数ω于区间[a,b]→Rn,对于实对称矩阵Z(∈ Rn×n) > 0,则下述不等式(2)应成立: 引理2:有f(s) =a2s2+a1s+a0二次函数,如果以下3个不等式成立,则f(s)<0,s∈ [ 0,h] 。 (i)f(0)<0;(ii)f(h)<0;(iii)-h2a2+f( 0) < 0。 引理3:定义ϖ1、ϖ2是Rn上的可导函数,标量α∈ ( 0,1),对于实对称矩阵ℜ1、ℜ2(∈ Rn×n) > 0,任意矩阵Y1,Y2∈Rn×n有积分不等式(8)成立: 首先,定义向量、矩阵如下: 对于系统(1),有如下稳定性判据: 定理 1:存在实对称矩阵P(∈ R5n×5n)>0,R(∈ Rn×n) > 0,任 意 矩 阵Y1、Y2∈R3n×3n, 对 于条件,如果下列不等式组(18)~(20)成立,则系统(1)稳定。 式中: 证明:根据Lyapunov稳定分析需求,构建新的增广型Lyapunov-Krasovskii泛函如下: 当P>0,R>0时,则函数正定,即V(xt)>0。对V(xt)求导可得: 由引理1得: 由引理3得: 结合式(40)~(43),得: 本节以典型二阶时滞系统、四机11节点时滞电力系统为例,验证文章所提方法的优越性。 (1)考虑如下典型系统1: (2)考虑如下典型系统2: 利用文献[13-15]的方法及定理 1计算,仿真得到系统的稳定裕度,结果见表1、表2。 表1 典型系统1的稳定裕度hTab.1 S tability margin h of typical system 1 表2 典型系统2的稳定裕度hTab.2 S tability margin h of typical system 2 从上表1、2中可明显看出,较文献[13-15],定理1得到的稳定裕度更大一些,由此表明文章所提方法的优越性。 了进一步验证文章方法的实用性和有效性,考虑如图1所示四机11节点电力系统[16]。 图1 四机11节点系统Fig.1 Four-machine 11-bus power system 状态矩阵如下: 利用文献[13-15]的方法及定理 1计算,仿真得到四机 11节点电力系统的稳定裕度,结果见表3。 表3 四机11节点系统的稳定裕度hTab.3 Stability margin h of four-machine 11-bus system 从表3可以明显看出,较文献[13-15],定理1得到的稳定裕度更大一些,由此表明文章所提方法具有更小的保守性。 文章为了得到更大的时滞稳定裕度,以及满足Lyapunov稳定分析的需求,提出一种新的增广型Lyapunov-Krasovskii泛函,合理地利用一种逆凸不等式处理泛函求导后的积分项。通过分析推导,给出了含时变时滞的电力系统稳定判据,大大降低了现有结果的保守性。最后,以典型二阶时滞系统、四机11节点系统为实例,通过仿真分析得到系统的时滞稳定裕度,与现有文献相比,表明了文章方法的优越性。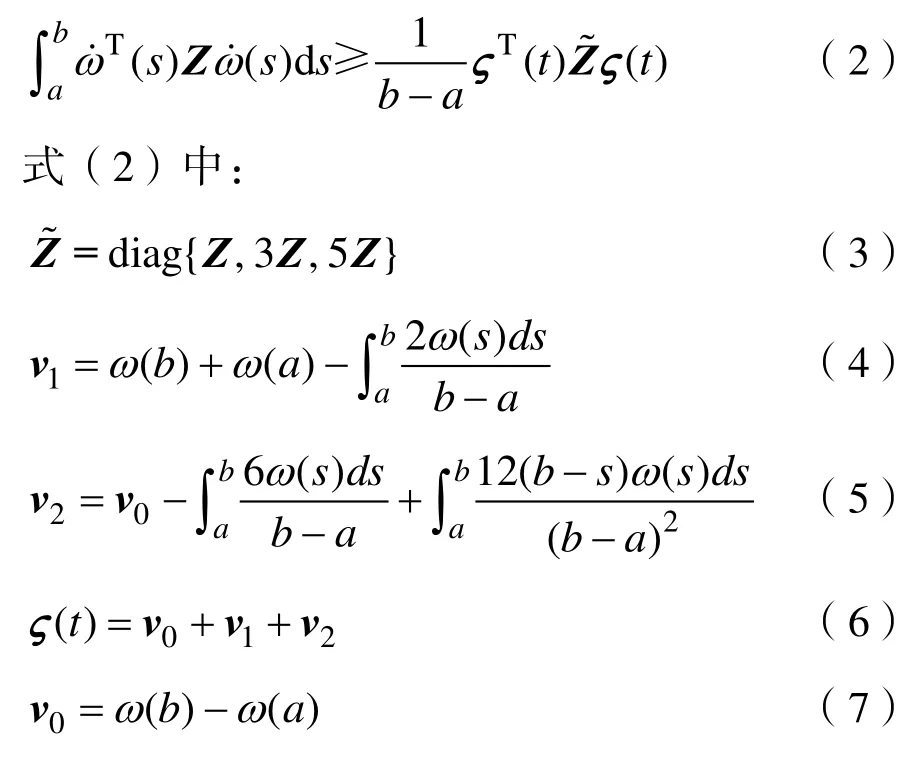
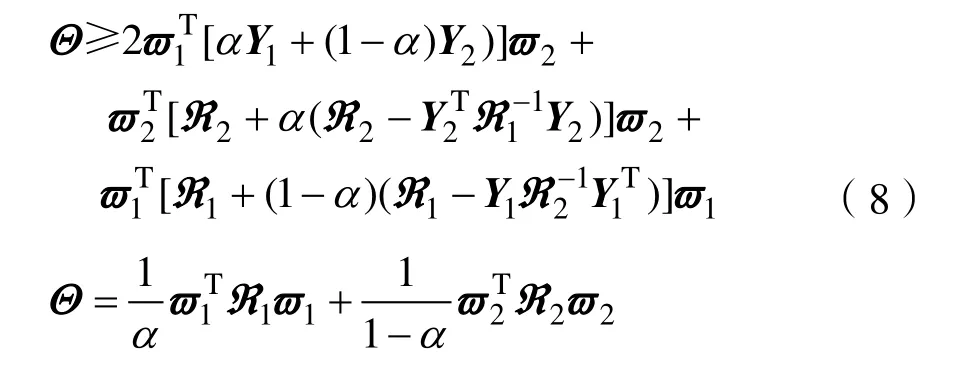
2 稳定判据

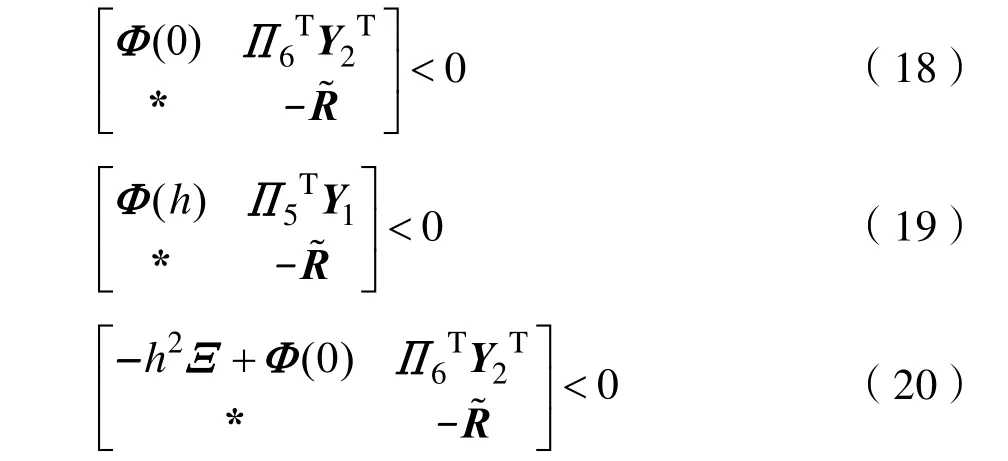
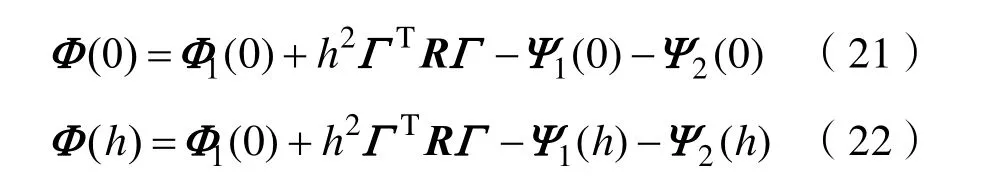
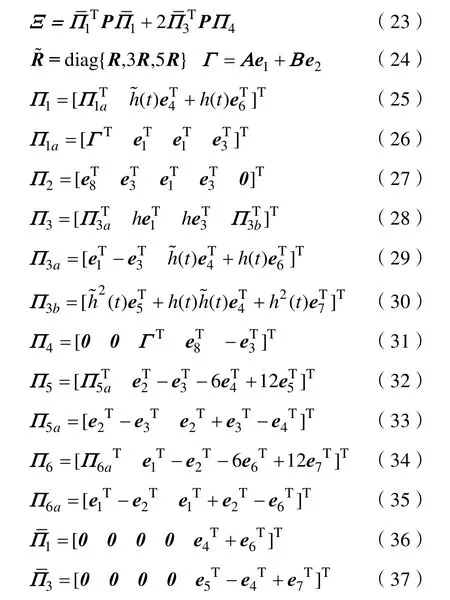
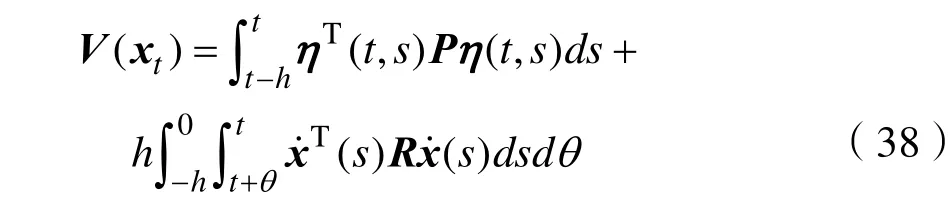
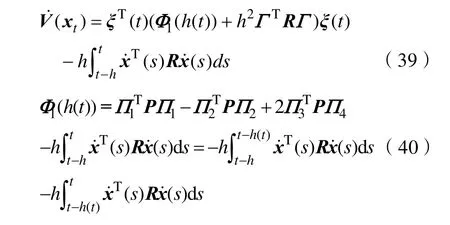
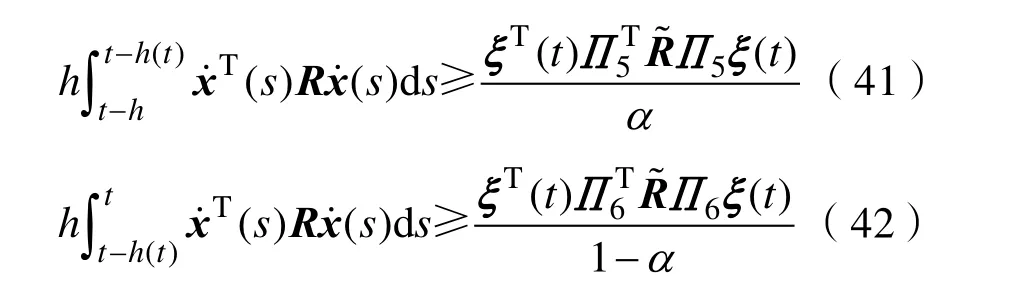

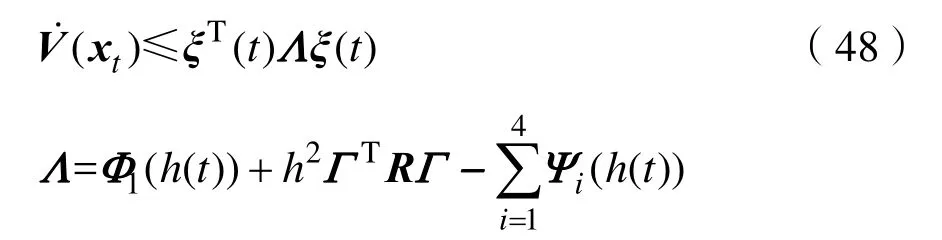
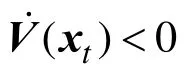
3 案例分析
3.1 典型二阶时滞系统




3.2 四机11节点系统
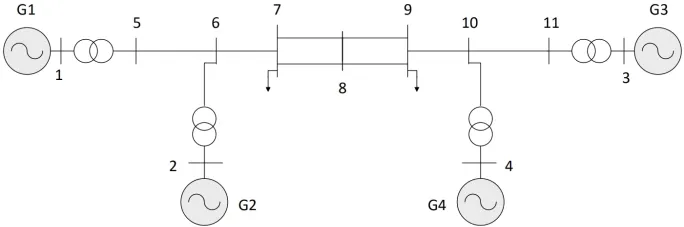


4 结论

