基于CEEMDAN和SCA-MRVM的滚动轴承故障诊断

陈世鹏，杨奕飞，张林，张洪武

(1．江苏科技大学 电子信息学院，江苏 镇江 212003；2．陆军装备部驻沈阳军代局驻哈尔滨地区军代室，哈尔滨 150000；3．镇江船舶电器有限责任公司，江苏 镇江 212002)

滚动轴承是船舶推进系统、甲板机械设备中广泛应用的基础部件，其作用是将运转的轴与轴座之间的滑动摩擦变为滚动摩擦，从而减少摩擦损失。滚动轴承运行状态的稳定性对机械设备有重要影响，对其故障进行准确诊断能保障机械系统平稳高效运行。

振动检测法是滚动轴承最常用的诊断方法，轴承的振动信号具有非线性、非平稳的特点，传统的时域、频域分析方法不能有效提取故障特征；短时傅里叶只适用于缓慢变化的信号[1]；小波变换对信号的处理缺乏自适应性[2]。经验模态分解(EMD)[3]采用自适应基的时频局部化分析，克服了基函数无自适应性的问题，但存在端点效应和模态混叠的问题。自适应噪声完备集合经验模态分解(Complete Ensemble Empirical Mode Decomposition with Adaptive Noise, CEEMDAN)能有效解决EMD的模态混叠问题，减小重构误差并提高分解效率，在轴承特征提取方面有良好表现[4-5]。

在工程实际中，监测所得通常是大量正常数据和样本量较小的故障数据，支持向量机(SVM)适合处理小样本问题，但存在核函数必须满足Mercer条件、模型稀疏性不强等不足[6-7]。相关向量机(Relevance Vector Machine,RVM)[8]具有核函数无需满足Mercer条件，稀疏性更强，所需参数少，输出概率式分布结果等优点，在小样本、非线性回归和分类问题上也有很好的应用[9-10]。RVM中核函数和核参数对预测结果影响很大，多核学习通过组合基础核函数获得多种核函数的优点[11-12]，可用于构建多核相关向量机(Multi-kernel Relevance Vector Machine,MRVM)，从而获得学习能力和泛化能力。滚动轴承的故障诊断为多分类问题，应用最广泛的一对一算法会产生无效投票和分类不确定性问题[13]，可通过智能优化算法进行模型参数的优选，常见算法如粒子群优化(PSO)算法易陷入局部最优，后期迭代收敛慢，寻优精度较低[14]；遗传算法(GA)的编码解码过程复杂，算子选择依赖经验，收敛速度慢[15]；正余弦算法(Sine Cosine Algorithm,SCA)[16]参数少，结构简单，收敛速度快，全局寻优能力强。

鉴于上述算法的特点，提出了一种基于CEEMDAN和SCA-MRVM的滚动轴承故障诊断方法，以实现滚动轴承运行状态识别并提高分类精度。

1 基于CEEMDAN的特征提取

自适应噪声完备集合经验模态分解在经验模态分解的每个阶段加入有限次的自适应白噪声，从而抑制模态混叠问题，其重构误差几乎为零，同时解决了集合经验模态分解的不完备性和计算效率低的问题，该算法的主要步骤为：

1)对给定信号X(t)，在分解中采用Volterra模型进行端点数据预测延拓，从而抑制包络线在端点处的发散，分解得到本征模态分量(Intrinsic Mode Functions,IMF)。对加入高斯分布白噪声Di(i=1,2,…,I)的信号Xi进行分解获得第1个模态分量c1，即

(1)

2)计算第1个余量

r1(t)=X(t)-c1。

(2)

3)对信号r1(t)+εE1(Di(t))进行分解，得到第2个模态分量c2,即

(3)

式中：ε为自适应系数。

4)对于j=2,3,…,n，先求出第j个余量rj(t)，再计算第j+1个模态分量,即

rj(t)=rj-1(t)-cj，

(4)

(5)

式中：Ej为经验模态分解得到的第j个分量。

5)重复执行以上步骤，直到余量不能被分解时结束，最终余量为rn(t)，原信号可以表示为

(6)

振动信号经过CEEMDAN处理后，被分解为一系列瞬时频率由高到低的IMF分量，能量主要集中在前几个分量，具体特征提取步骤如下：

1)计算各IMF分量的能量ej

(7)

式中：cjk为第j个IMF分量离散点的幅值；n为分量个数；N为采样点数。

(8)

(9)

式中：ai为瞬时振幅。

3)计算能量熵H

(10)

4)构造特征向量X

(11)

2 多核相关向量机

2.1 相关向量机

(12)

式中：wi为模型权重；K(x,xi)为核函数。

将logistic sigmoid连接函数σ(y)=1/(1+e-y)应用于y(x)，则p(t|x)服从伯努利分布。假设样本集独立同分布，则整个样本集的似然函数为

(13)

t=(t1,t2,…,tN)T,

w=(w0,w1,…,wN)T。

在贝叶斯框架下，通过最大化似然函数估计参数w，为避免过学习，相关向量机为每个权重定义了高斯先验概率分布来约束参数，即

(14)

式中：αi为N+1维超参数。为每个权重引入超参数是相关向量机的重要特征，这最终导致了算法求解的稀疏性。

由贝叶斯定理可得

(15)

因为p(w|t,α)∞p(t|w)p(w|α)，所以将w的最大后验估计等价为最大化，即

logp(w|t,α)=log{p(t|w)p(w|α)}=

(16)

A=diag(α0,α1,…,αN),yn=σ{y(xn;w)}。

由于p(α|t)∞p(t|α)p(α)，对p(α|t) 的求解可转化为p(t|α)关于α最大化的问题，只需对p(t|α)最大化，即

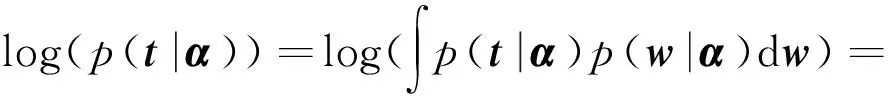
(17)

通过拉普拉斯方法求解(16)式和(17)式，不断迭代以优化参数w和超参数α，最终只有少量的wi趋于稳定的有限值，其他大部分wi将趋于0，非零的wi对应的xi即为相关向量。相关向量机的分类策略为：当σ(yi)=1/(1+e-yi)<0.5 时，标签值ti=0；反之，ti=1。这样相关向量机的二分类模型就获得了样本的类别信息和后验概率，此概率表示分类结果的不确定性。

2.2 改进的一对一多分类

滚动轴承故障诊断属于多分类问题，需要采用合适的方法将基础的二分类器扩展为多分类器。在一个二分类器中，如果输入样本的类别不属于这2类，就会产生无效投票，基础一对一算法便会产生大量无效投票；一对一多分类模型中若不止一类获得最多票，就会产生分类的不确定性。为有效提高相关向量机多分类模型的分类精度和可信度，本文使用一种改进的一对一多分类算法：

1)在训练阶段，按基础一对一分类方法，假设样本共有k类，则任意i,j(i=1,2,…,k;j=1,2,…,k;i≠j)2类可以建立一个RVM二分类器Ri,j，此时共k(k-1)/2个二分类器；再建立i类与除去i,j类的其他类rest构成的二分类器Ri,rest，j类与除去i,j类的其他类rest构成的二分类器Rj,rest；则对所有样本共建立了3k(k-1)/2个二分类器。

2)在测试阶段，测试样本通过改进的相关向量机多分类模型，若Ri,j，Ri,rest，Rj,rest这3个分类器中i类或j类获得2票，则i类或j类加1票；若其他类rest获得2票，则不计入票数；若i,j,rest类各1票，则计算各自的分类决策函数值,概率值最大者为样本对应类别，类别若属于i或j类，则计入对应类别票数，若为rest类则不计入。这样可有效减少无效投票。针对分类的不确定性问题，即最高票数类不止1个时，通过累加对应分类器的决策函数值，概率之和最大者对应的标签即为样本所属类别。

2.3 多核相关向量机

核函数在相关向量机分类模型中起着关键作用，是决定模型诊断准确率的重要因素。核函数分为全局核函数和局部核函数，全局核函数有较强的泛化能力，局部核函数有较强的非线性逼近能力。单核相关向量机简单易实现，但在模型训练中不能完全挖掘数据的有用信息，模型泛化能力不强。

为使相关向量机具有更好的学习能力和泛化能力，引入权重参数将全局核函数和局部核函数结合起来构造多核相关向量机，其中全局核选择多项式核函数Kpoly(x,xi)，局部核选择高斯核函数KRBF(x,xi)，其表达式分别为

Kpoly(x,xi)=(xxi+1)d，

(18)

(19)

则构造的混合核函数为

K=αKpoly(x,xi)+(1-α)KRBF(x,xi)，

(20)

式中：d为多项式核函数的阶数；σ为高斯核函数的宽度；α为权重参数，0≤α≤1。

3 基于SCA-MRVM的识别模型

3.1 正余弦算法

正余弦算法是基于种群的随机优化算法，其利用正余弦函数的性质使解向量振荡性地趋于全局最优，算法中自适应参数和随机性参数较好地平衡了算法的探索和开发能力。

在正余弦算法中，先进行个体位置初始化，再采用正余弦函数在后续迭代中更新个体位置，具体更新公式为

(21)

(22)

组合(21)和(22)式后的位置更新公式为

(23)

式中：r4为[0,1]内的随机数。

在上述3个公式中，r1,r2,r3,r4是正余弦算法的主要参数：最关键的是自适应参数r1，其决定了下一次迭代的位置，该位置是候选解与目标解之间的任一空间或之外的空间，r1值较大时算法偏向于全局搜索，r1值较小时算法倾向于局部开发；r2为[0,2π]内的随机数，定义了解的更新在移动方向(朝向或远离目标解)上的步长；r3为[0,2]内的随机数，给目标解随机赋予一个权值，作用是表明当前最优解对候选解的影响程度；r4表示如何在(23)式中的正弦或余弦分量之间切换，当r4<0.5时，按正弦公式迭代，当r4>0.5时，按余弦公式迭代。

为保证正余弦算法最终能收敛到全局最优解，需实现正弦和余弦函数的自适应调节以平衡全局搜索和局部开发，自适应调节公式为

(24)

式中：T为最大迭代次数；t为当前迭代次数；a为常数。

3.2 多核相关向量机的参数优化

为进一步提高分类精度和可信度，采用正余弦算法对多核相关向量机的权重参数α、多项式核参数d和高斯核参数σ进行寻优，即通过正余弦算法搜寻一组向量[α,d,σ],使多核相关向量机模型的识别率最高。选择分类准确率作为多核相关向量机的适应度函数。

优化的具体步骤如下：

1)初始化正余弦算法和多核相关向量机的参数，如种群规模N、最大迭代次数T、常数a。设定权重参数α、核参数d与σ的搜索范围，设置算法终止条件并初始化候选解空间位置X=[X1,X2,…,XN]，其中Xi=[α,d,σ]。

2)计算种群候选解的第1次迭代适应度值，并保存当前种群中的最佳候选解。

3)通过(24)式计算参数r1，利用(23)式更新候选解位置。

4)计算新候选解的适应度值并与之前最佳候选解的适应度值对比，若当前候选解优于之前最佳候选解，就保存当前候选解为最佳候选解，反之保留之前最佳候选解。

5)判断算法是否满足终止条件，若不满足，则迭代次数加1，即t=t+1，并返回步骤3，若满足则转到下一步。

6)停止迭代，输出最优候选解适应度值和所处空间位置，即[α,d,σ]值。

4 基于CEEMDAN和SCA-MRVM的滚动轴承故障诊断

4.1 故障诊断流程

基于CEEMDAN和SCA-MRVM的故障诊断流程如图1所示，主要步骤如下：

图1 基于SCA-MRVM的故障诊断流程

1)采集滚动轴承振动信号，并划分为训练集和测试集。

2)采用自适应噪声完备集合经验模态分解处理信号并提取特征。

3)通过训练集训练多核相关向量机模型，同时采用正余弦算法进行参数优化。

4)将测试集输入到优化后的多核相关向量机模型，输出诊断结果。

4.2 试验一

4.2.1 试验数据集

采用Case Western Reserve University滚动轴承振动数据进行试验分析，驱动端轴承为SKF6205，利用加速度振动传感器采集数据，电动机转速为1 750 r/min，采样频率为12 kHz，具体故障类型分布和样本划分见表1。

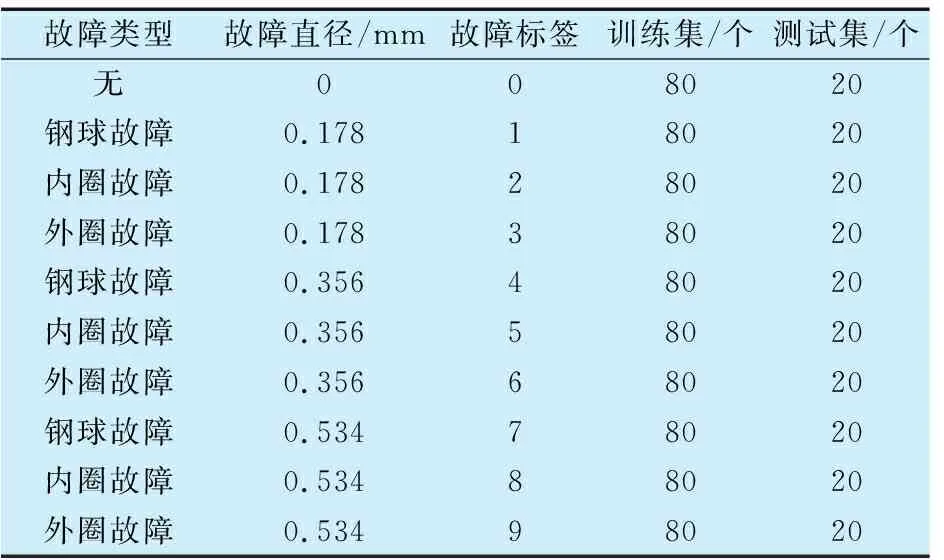
表1 试验轴承故障类型和样本划分

4.2.2 模型参数优化

采用正余弦算法对多核相关向量机模型的3个参数进行寻优，并与PSO和GA算法寻优结果进行性能对比。具体仿真参数为：MRVM的权重参数α∈[0,1]，多项式核参数d∈[0,100]，高斯核参数σ∈[0.01,1 000]；SCA，PSO和GA的迭代次数T为300，种群大小N为20；SCA中常数a为2；PSO中学习因子c1和c2分别为1.5和1.7；GA中交叉概率为0.7，变异概率为0.01。通过仿真得到的各算法的适应度曲线如图2所示。

由图2可知：SCA在迭代40次左右完成收敛，且达到3种算法中最好的寻优结果；PSO在迭代120次左右收敛到最优结果，收敛速度慢于SCA，寻优结果比SCA和GA都差；GA在迭代150次左右收敛到最优结果，收敛速度慢于SCA与PSO，寻优结果弱于SCA。综上所述，SCA收敛速度快且能达到更好的寻优结果，更适合MRVM的参数优化。

图2 SCA，PSO和GA对MRVM参数的寻优过程

4.2.3 诊断结果分析

采用SCA-MRVM模型、PSO-MRVM模型和GA-MRVM模型分别对滚动轴承的故障数据进行分类并计算其诊断准确率。用200个数据作为测试样本输入到3种模型中进行识别，测试集分类结果如图3所示，不同算法模型的诊断准确率见表2。由图3及表2可知：SCA-MRVM模型能将滚动轴承的10类故障数据完全区分，不会出现混叠现象，诊断准确率达到100%；PSO-MRVM模型和GA-MRVM模型能基本识别出故障，但在外圈重度故障、内圈中度故障和钢球轻度故障识别中有一定的混叠现象，诊断准确率分别为95%，96%，区分度低于SCA-MRVM模型。

图3 不同算法模型对测试集的分类结果

表2 不同算法模型的诊断准确率

4.3 试验二

为进一步验证SCA-MRVM模型的有效性，应用风机滚动轴承故障试验数据进行分析。试验所用加速度传感器为PCBMA352A60，测点在垂直轴承座方向，转速分为600，800，1 000 r/min，采样频率50 kHz，轴承的各项参数见表3。轴承的故障是人为通过切割技术分别在轴承滚子、内圈和外圈加工出微小线状伤痕(图4)。

表3 轴承相关参数

图4 轴承故障类型

在不同工况下采集了3组数据，每组数据均包含正常、滚子故障、内圈故障和外圈故障4种状态，每种工作状态的采样时间均为55 s。

表4 试验数据的相关参数

基于上述数据，采用自适应噪声完备集合经验模态分解分解信号，并通过(7)—(11)式进行特征提取，然后将训练集特征向量分别输入到SCA-MRVM，PSO-MRVM和GA-MRVM模型进行参数优化和模型训练，最后用训练好的模型在测试集上进行状态识别与诊断。各模型对测试集样本的诊断准确率见表5：SCA-MRVM模型的平均诊断准确率为97.5%，高于PSO-MRVM模型的93.5%和GA-MRVM模型的94.3%；SCA-MRVM模型在不同尺寸故障和不同类型故障中都能做到较高的区分度，混叠现象明显少于PSO-MRVM模型和GA-MRVM模型，表明SCA-MRVM模型适应性更好，能达到更高的故障诊断精度。

表5 不同算法的诊断准确率

5 结束语

提出了一种基于CEEMDAN和SCA-MRVM模型的轴承故障诊断方法，对样本少、非线性、非平稳的滚动轴承振动信号进行故障模式识别研究。试验结果表明SCA-MRVM模型的参数设置简单，在小样本训练下具有很高的诊断精度，全局寻优能力和分类准确率均优于PSO和GA优化的模型，具有较好的实用性。

但本研究尚未考虑样本数据的不平衡(如类间不平衡)，正余弦算法还有改进空间，如改进转换参数 ，结合使用凹函数和凸函数来平衡算法的全局搜索和局部开发能力等，这些将是下一步的研究方向。