基于热-应力耦合的高速圆柱滚子轴承凸度值分析

倪艳光，刘晗,邓四二,时大方,刘彬

(1.河南科技大学 机电工程学院，河南 洛阳 471003;2.浙江天马轴承股份有限公司 博士后工作站，杭州 310015;3.浙江天马轴承股份有限公司，杭州 310015)

圆柱滚子轴承在高速运转时，由于滚子与套圈之间存在应力集中现象，套圈易受到不同程度的损伤，从而降低轴承疲劳寿命，故有必要对圆柱滚子轴承滚子凸度进行合理设计并分析凸度值对轴承力学特性的影响。

近年来，国内外对圆柱滚子轴承滚子凸度做了大量研究。文献[1-2]建立了圆柱滚子轴承有限元模型，分析了不同素线修形滚子对轴承力学性能的影响，对数素线修形能够极大地改善滚子端部的应力集中现象；文献[3-4]基于弹性半空间理论，基于有限元法分析了素线修形滚子在倾斜状态下与滚道的接触应力分布情况及轴承疲劳寿命；文献[5-7]基于有限元软件，对修形后的圆柱滚子轴承进行力学性能分析，分析了不同凸度值下滚子的接触应力分布情况，结果表明在不同工况下滚子最佳凸度值应相对应的改变以保证滚子受力最小；文献[8]基于有限元法对修形滚子的凸度偏移量进行分析，结果表明凸度偏移量对接触应力影响较大，偏移量会造成接触应力分布不均匀；文献[9]通过试验验证了滚子凸度值对轴承疲劳寿命的影响，试验结果表明在特定工况下最优凸度值可以提高轴承疲劳寿命。

上述研究仅考虑了滚子凸度对轴承力学性能的影响，缺乏考虑圆柱滚子轴承尤其是高速圆柱滚子轴承使用过程中的热-应力耦合因素对滚子接触应力分布的影响。鉴于此，以圆柱滚子轴承为研究对象，在轴承动力学和有限元热分析理论的基础上，对轴承各零件之间的摩擦功耗和温度场进行计算，建立高速圆柱滚子轴承热-应力耦合分析模型，分析凸度值对轴承接触应力、温升及热应力的影响，得到滚子最优凸度值。

1 圆柱滚子轴承热分析

引起圆柱滚子轴承温度变化的原因主要有：1)轴承各零件摩擦引起的功率损失；2)轴承与外部环境通过传导、对流等方式进行的热交换。故圆柱滚子轴承热分析模型应能够准确进行摩擦功耗计算和温度场分析。

1.1 摩擦功耗计算模型

基于滚动轴承动力学、接触力学以及弹流润滑理论建立圆柱滚子轴承动力学方程，求解后得到一定工况下轴承各零件间相互作用力和运动参数，从而确定轴承运动状态。在此基础上建立圆柱滚子轴承摩擦功耗求解模型，圆柱滚子轴承各零件之间的摩擦功耗包括[10]：1)滚子与滚道之间由材料的弹性滞后引起的摩擦功耗；2)滚子与滚道之间由滑动引起的摩擦功耗；3)滚子与保持架之间的摩擦功耗；4)保持架与套圈挡边之间由滑动引起的摩擦功耗；5)滚子受润滑剂的黏性摩擦引起的摩擦功耗。

滚子与滚道之间由材料的弹性滞后引起的摩擦功耗为

(1)

式中：Z为滚子数量；Dpw为滚子组节圆直径；ah为弹性滞后损失系数；Qj为第j个滚子与套圈的接触载荷；bj为第j个滚子与套圈的接触椭圆短半轴；R为当量半径；ωbj为第j个滚子的自转角速度；下标i，e分别代表内圈和外圈。

滚子与滚道之间由滑动引起的摩擦功耗为

(2)

式中：Tj为第j个滚子与套圈滚道的摩擦力；Vj为第j个滚子与套圈的相对滑动速度。

滚子与保持架之间的摩擦功耗为

(3)

FTBR=μFB，

FTFR=μFF，

式中：vr为滚子与保持架的相对滑动速度；FB为保持架对滚子的作用力；FF为滚子对保持架的作用力；μ为摩擦因数；η0为润滑剂动力黏度；u为滚子自转线速度；L为滚子有效接触长度；F为滚子与保持架的法向作用力。

保持架与套圈挡边之间由滑动引起的摩擦功耗为

ML=ωcMcx，

(4)

式中：ωc为保持架角速度；Mcx为油膜对保持架的摩擦力矩。

滚子受润滑剂的黏性摩擦引起的摩擦功耗为

(5)

式中：Fv为滚子所受的黏性阻力[11]。

圆柱滚子轴承在高速转动时由于摩擦而产生的摩擦功耗为

MR=ME+Mh+Mc+ML+Moil。

(6)

1.2 热传递计算模型

轴承在运转过程中，各零件产生的摩擦功耗不同，生成的热量也不同，这些热量将通过热传导、热对流及热辐射的方式进行热交换。在此仅对单套轴承进行热分析，考虑到轴承零件由热辐射传递的热量较小，可以忽略不计。建模时忽略轴承座和轴，在轴承外圈外表面和内圈内表面与空气接触部位设置为热对流，滚子与内、外圈接触部位设置为热传导。

1.2.1 热传导

热传导[12]遵循傅里叶定律，即

(7)

1.2.2 热对流

温度场分析中的热对流设置为面载荷的形式[12]，热对流产生的热量为

q*=hf(TS-TB)，

(8)

式中：hf为热对流热量传递系数；TS为固体表面温度；TB为流体温度。

2 圆柱滚子轴承温度场模型

以某圆柱滚子轴承为例分析，其主要结构参数见表1。轴承零件材料均为GCr15，材料参数为：泊松比0.3，密度7 850 kg/m3，弹性模量207 GPa，热膨胀系数1.04×10-5。转速为9 000 r/min，径向载荷为26 kN，结果通过计算可得圆柱滚子轴承各零件的摩擦功耗,结果见表2。

表1 圆柱滚子轴承主要结构参数Tab.1 Main structural parameters of cylindrical roller bearing

表2 圆柱滚子轴承各零件的摩擦功耗Tab.2 Friction power consumption of various parts of cylindrical roller bearing

滚子素线采用对数修形设计方法[13]，对数修形的素线方程为

(9)

式中：ν为材料泊松比；E为材料弹性模量；Q为滚子所受载荷；Lwe为滚子有效长度。

修形后的滚子凸度值δ可按照(10)—(12)式计算，即

(10)

(11)

(12)

式中：K0=2.81×10-6mm2/N；Dwe为滚子有效直径。

经计算可得滚子理论凸度值δ为16.59 μm。

2.1 有限元分析模型

为提高有限元计算效率，取单个滚子的1/2建立轴承分析模型，在滚子与内、外圈滚道的接触部位建立接触对，内、外圈滚道采用TARGET170单元作为目标面，滚子采用CONTACT174单元作为接触面，用SOLID90六面体实体单元对圆柱滚子轴承进行网格划分，接触部位网格细化，如图1所示。将环境温度22 ℃设置为热分析时的初始温度，设置轴承表面的对流系数和接触部位的生热率。将表2中所求得的摩擦功耗平均分配到圆柱滚子轴承的接触区域，作为轴承热分析的边界条件。

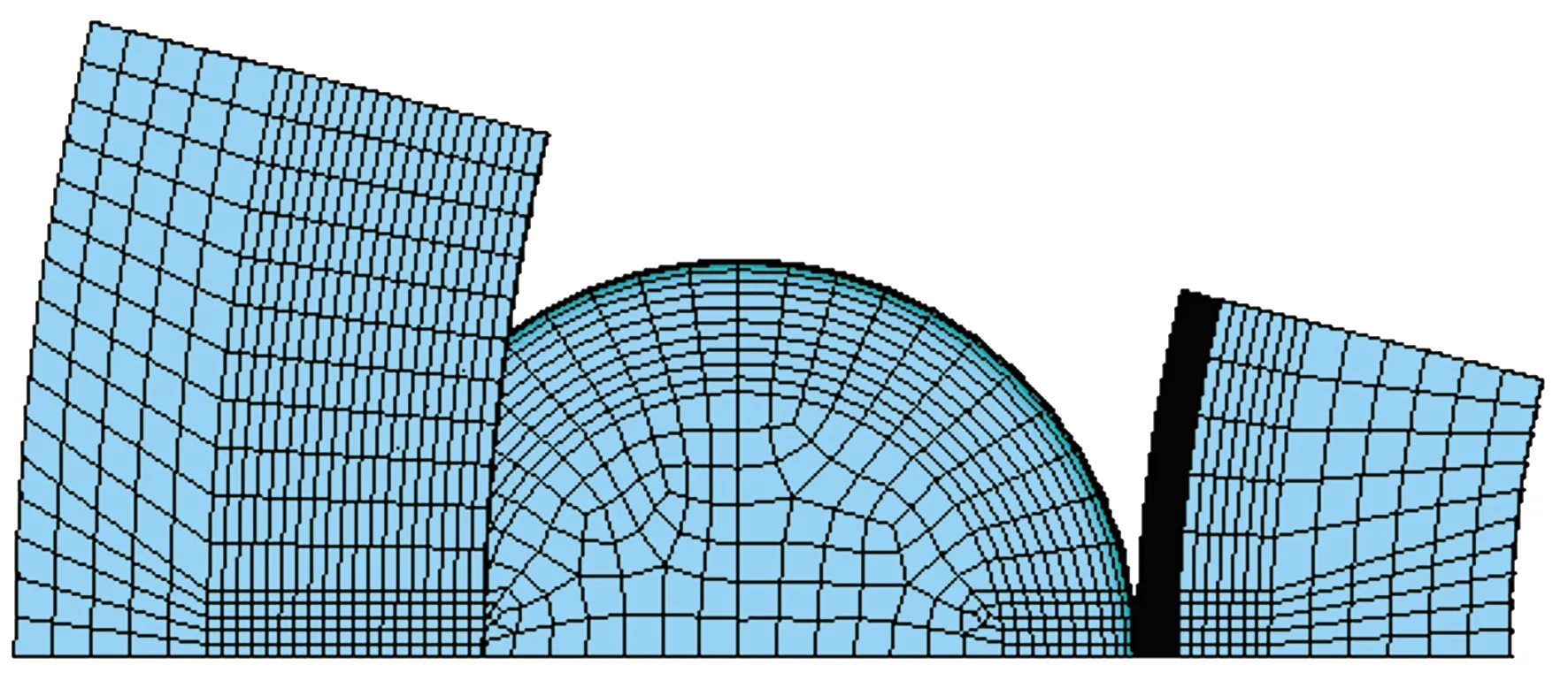
图1 圆柱滚子轴承有限元分析模型Fig.1 Finite element analysis model of cylindrical roller bearing

2.2 温度场分析

对修形后的圆柱滚子轴承进行稳态温度场分析，结果如图2、图3所示，由图可知：最高温度在滚子与内圈接触处，这是由于轴承转动时滚子与内圈接触处产生的摩擦功耗最多；最低温度在外圈上，这是由于外圈摩擦功耗小且与外界接触面积大、散热快。

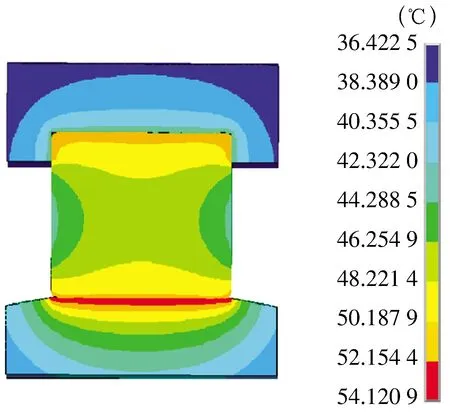
图2 圆柱滚子轴承温度场云图Fig.2 Temperature field nephogram of cylindrical roller bearing

图3 滚子温度场云图Fig.3 Temperature field nephogram of roller

计算修形后滚子最高温度随滚子凸度值的变化如图4所示，由图可知：随滚子凸度值增大，滚子最高温度也随之增大。这是因为滚子凸度值越大，滚子与滚道的接触面积越小，滚子生热后通过热传导传递给套圈的热量减小，滚子最高温度会随凸度增大而增大。

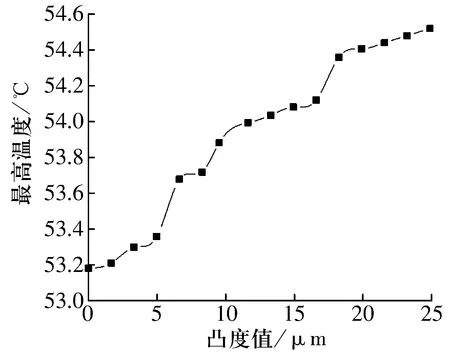
图4 滚子最高温度随凸度值的变化曲线Fig.4 Variation curve of maximum temperature of roller with crowning value

3 圆柱滚子轴承热-应力分析

由于轴承温升对应力分布有很大影响，采用间接耦合法对轴承的热-应力进行分析。通过ETCHG命令将温度场单元转换成SOLID186实体单元，以保证耦合场中的网格单元节点数与之前温度场网格单元节点数对应。把热分析结果作为耦合场热-应力分析的边界条件，对圆柱滚子轴承施加约束和载荷。

考虑热-应力耦合后滚子与内圈滚道接触处的接触应力分布如图5所示(横坐标原点位置对应滚子轴线的中点)，由图可以看出：1)接触应力沿滚子轴线方向呈对称分布；2)当凸度值较小时，滚子两端为主要承载区，端部边缘处出现应力集中现象；3)随凸度值增加，滚子中部位置为主要承载区，接触应力值从滚子中部到两端逐渐下降，应力集中得到改善，当凸度值增加到21.57 μm(1.3δ)时，最大接触应力为1 876.99 MPa，此后滚子最大接触应力随凸度值增大而增大。故在该工况下滚子最优凸度值为21.57 μm。

图5 接触应力沿滚子轴向分布曲线图Fig.5 Distribution curve of contact stress along axial direction of roller

未考虑和考虑热-应力耦合2种情况下，滚子与套圈的最大接触应力随滚子凸度值的变化如图6所示，由图可知：1)考虑热-应力耦合时滚子与内、外圈的最大接触应力高于未考虑耦合时的最大接触应力，这是由于当考虑轴承的摩擦功耗和温度场变化时，轴承各零件发生热膨胀；2)2种情况下最大接触应力随滚子凸度值的增大均呈先减小后增大的趋势，但2条曲线拐点(最大接触应力值最小)对应的凸度值不同，未考虑热-应力耦合的最优凸度值为18.25 μm(1.1δ)，而考虑热-应力耦合的最优凸度值为21.57 μm(1.3δ)。

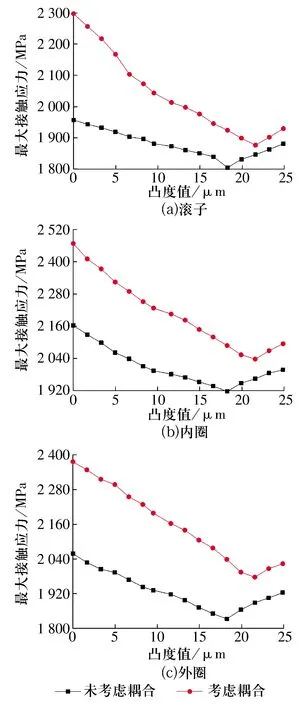
图6 各零件最大接触应力随凸度值的变化曲线Fig.6 Variation curve of maximum contact stress of each part with crowning value

4 最优凸度值分析

4.1 径向载荷对最优凸度值的影响

轴承转速为9 000 r/min，径向载荷取14～26 kN，不同径向载荷下滚子最优凸度值如图7所示。由图7可以看出：随径向载荷增大，滚子最优凸度值增大，且在热-应力耦合作用下最优凸度值更大。这是因为在热-应力耦合作用下，轴承温度上升致使各零件发生热膨胀，滚子与内、外圈接触处产生更大的边缘应力集中，因此需要更大的凸度值来消除应力集中现象。

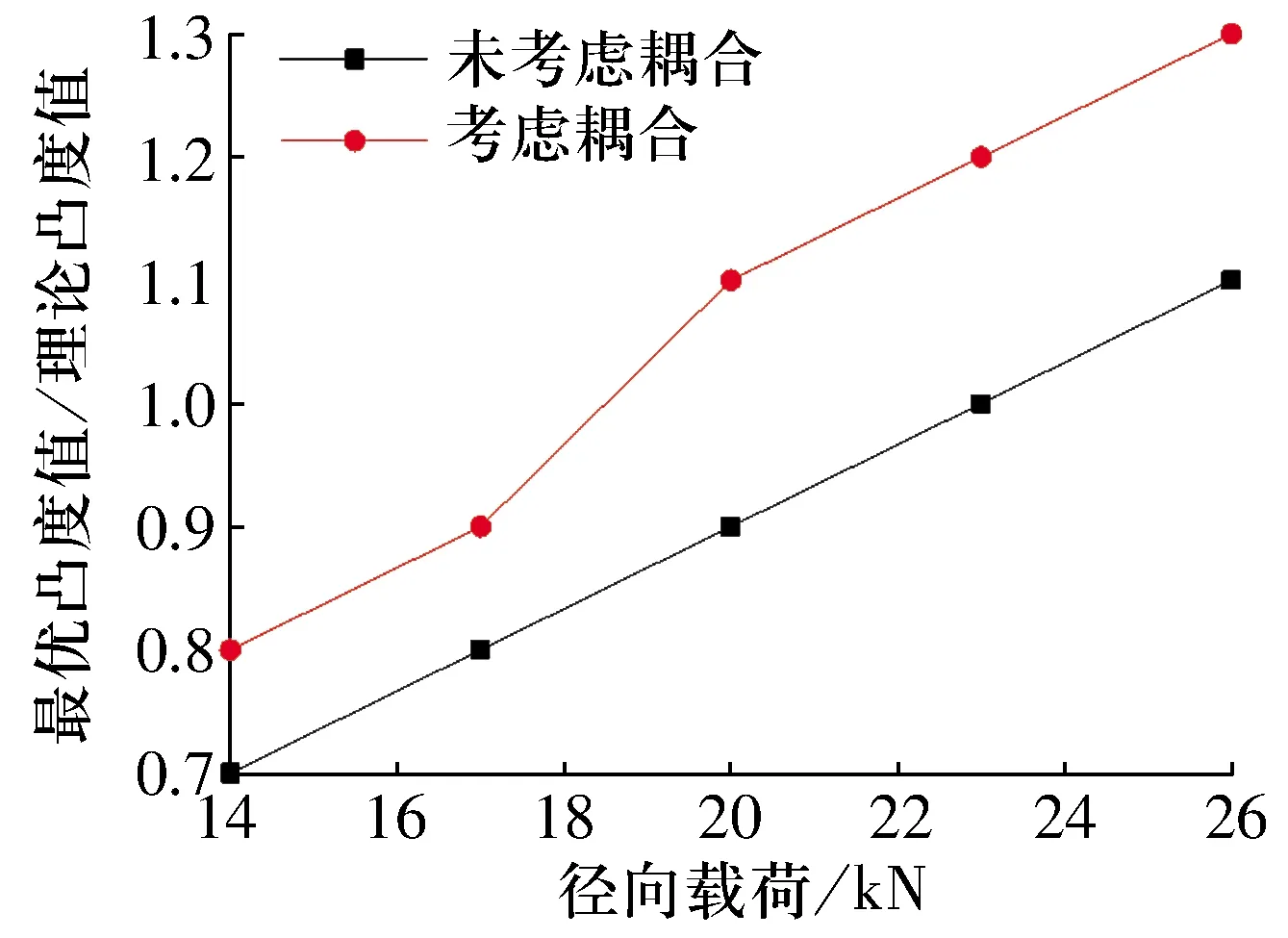
图7 滚子最优凸度值随径向载荷的变化曲线Fig.7 Variation curve of optimal crowning value of roller with radial load

4.2 转速对最优凸度值的影响

轴承径向载荷为20 kN，内圈转速取5 000～9 000 r/min，不同转速下滚子的最优凸度值如图8所示。由图8可以看出：考虑热-应力耦合作用时，随转速增大，滚子最优凸度值也随之增大,这是因为内圈转速增加导致轴承摩擦功耗随之增加，致使轴承温度上升，使得轴承各零件热膨胀，在滚子与内、外圈接触处产生更大的应力集中现象，而要消除这些应力集中需要相应的增加滚子凸度值;而未考虑热-应力耦合作用时，分析模型没有涉及温度变化对应力的影响，同时忽略了离心力，因此在转速变化时得到的接触应力没有变化，最优凸度值保持不变。

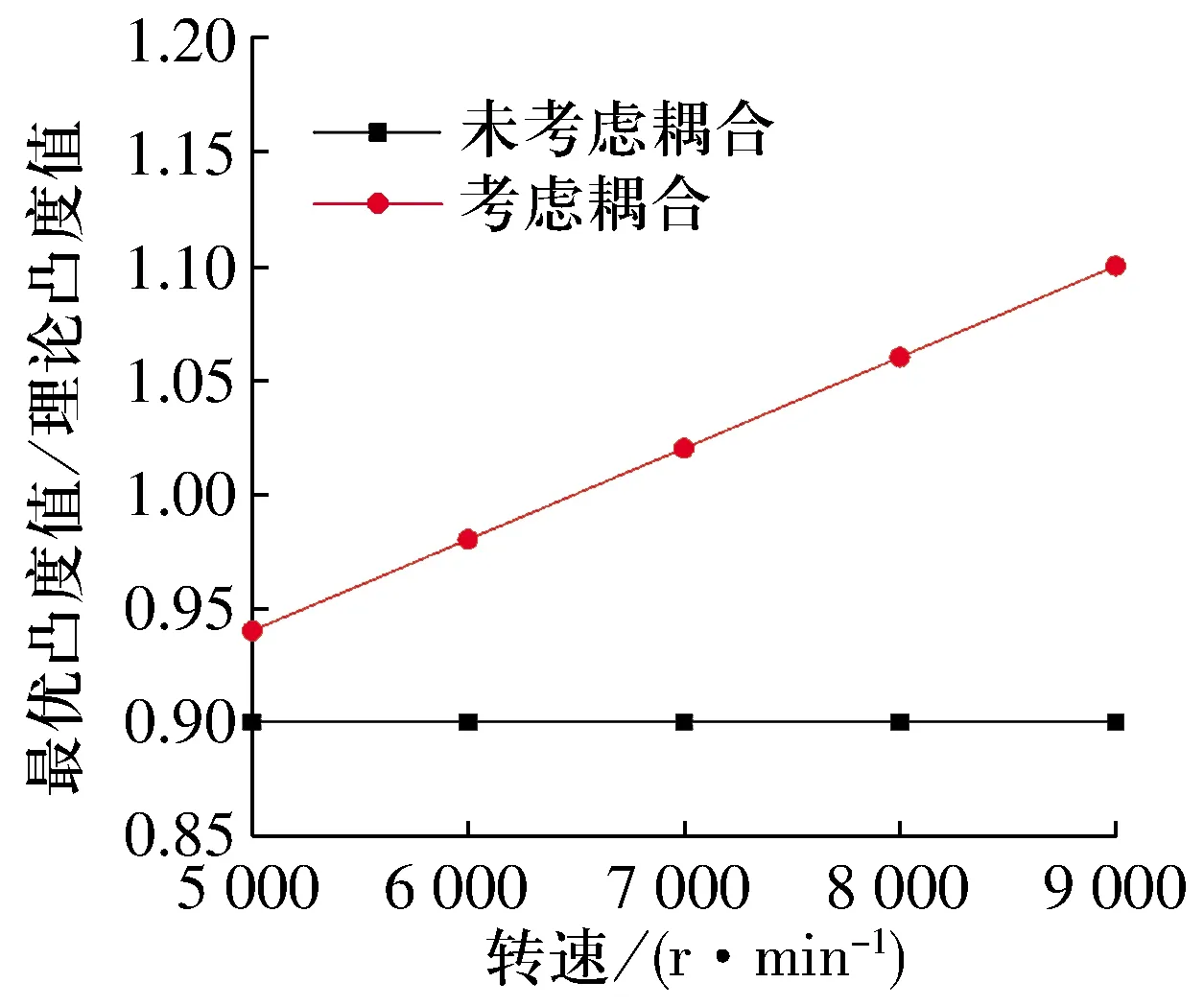
图8 滚子最优凸度值随转速的变化曲线Fig.8 Variation curve of optimal crowning value of roller with rotational speed

5 结论

考虑轴承热-应力之间的相互耦合作用，以轴承摩擦功耗计算和温度场分析为基础，建立了对数素线修形圆柱滚子轴承热-应力耦合分析模型并求解，得出以下结论：

1)在考虑热-应力耦合作用下，对数修形滚子存在一个最优凸度值，能有效地降低滚子最大接触应力。

2)由于考虑轴承温升引起的热膨胀，滚子与内、外圈之间的最大接触应力比未考虑耦合的最大接触应力要大，得出的滚子素线修形最优凸度值也有所不同。

3)不同工况对最优凸度值的选取均有影响，在圆柱滚子轴承设计中可针对具体的工况对滚子凸度进行优化设计。