基于改进最大相关峭度解卷积的滚动轴承复合故障诊断

朱丹宸，许骥，晋家兵，杜广森

(海军士官学校，安徽 蚌埠 233012)

滚动轴承是旋转机械的重要部件，其运行状态严重影响着整个设备的安全稳定性，因此开展滚动轴承的状态检测和故障诊断尤为重要。然而，由于设备结构较为复杂，轴承故障信号在传递过程中往往需要经过复杂的传递路径，导致轴承故障产生的周期性冲击成分容易淹没在背景噪声中。尤其在多故障并存的复合故障情况下，多故障特征的相互干扰会进一步加大复合故障特征分离和提取的难度。

近些年来，针对滚动轴承复合故障诊断开展了很多研究，如盲分离技术[1]、谱峭度方法[2]、变分模态分解(VMD)[3-4]、经验模式分解(EMD)[5]、辛几何模态分解(SGMD)[6]以及改进的时频谱分析方法[7]等，均取得了一定的效果。然而，上述方法大都将原始信号分解为不同频段的子信号，从不同子信号中提取出不同类型的故障特征，不仅算法本身的参数选取需深入研究，而且常需与其他方法相结合以避免噪声干扰并提高故障识别率。

考虑到复杂传递路径的影响，盲卷积方法也在复合故障诊断中得到了应用。如文献[8]提出了改进的最优最小熵反卷积方法，实现了齿轮箱复合故障特征的准确提取；文献[9]将最大相关峭度解卷积(MCKD)与谱峭度相结合，通过MCKD实现信号中故障成分的分离；考虑到MCKD输入参数选取的重要性，文献[10]提出了自适应MCKD方法，利用布谷鸟搜索算法自适应选取最优参数，通过对比证明了该方法的有效性；为进一步提高去噪能力，文献[11]在自适应MCKD的基础上引入定制的多小波变换，提高了复合故障特征提取的准确性，文献[12]利用排列熵和包络稀疏度对MCKD的参数进行选取，并结合总体局部均值分解方法实现了轴承的复合故障诊断。总体来看，MCKD的输入参数较多且有着严格要求，只有当所有参数都得到合理选取，MCKD才能发挥其在提取周期性故障冲击上的优越性[13]。

鉴于上述情况，考虑到滚动轴承复合故障的特点，以及强背景噪声干扰导致故障特征难以准确提取的问题，提出一种自适应MCKD方法，并将其与互相关谱相结合进行滚动轴承复合故障诊断。

1 自适应最大相关峭度解卷积

1.1 MCKD算法的基本原理

MCKD以相关峭度为指标，通过选取合适的滤波器进行解卷积，突出信号中被噪声掩盖的周期性脉冲成分，从而达到提高信噪比的效果。

周期信号y的相关峭度可以表示为[13]

(1)

式中：M为移位数，一般取1～7；T为迭代周期对应采样点的个数。

对于输入为xn，输出为yn的信号，其反向滤波过程可以表示为

(2)

式中：F为滤波器系数；L为滤波器长度；n为信号的采样点数。

MCKD的最终目标函数可以表示为

(3)

求解(3)式可得

(4)

r=mT,m=1,2,…,M，

则MCKD的迭代求解过程可以表示为：

1)选择周期T，滤波器上的L和移位数M；

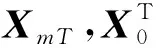
3)计算滤波得到的信号yn以及αm，β；

4)更新滤波器系数F；

5)如果滤波前后信号的ΔCKM(T)小于给定的阈值或者迭代次数达到设定的最大值，则停止迭代，否则返回步骤3。

1.2 改进的粒子群算法

(6)

经典粒子群优化算法的寻优过程缺乏多样性，搜索结果易出现局部最优解并提前收敛。为解决这些问题，采用基于正余弦加速系数的混合粒子群算法[14]，具体描述如下。

1)采用正、余弦表示学习因子c1和c2，即

(7)

(8)

式中：Mj为第j次迭代；Mmax为最大迭代数。

2)利用正弦函数对惯性权重ω的值进行更新，即

(9)

式中：ωk∈(0,1)；c为0～4之间的随机数；k为当前的迭代数，取值范围为1～Mmax。

3)采用反向学习(Opposition-Based Learning)代替随机取值的方法对种群进行初始化，提高PSO达到全局最优的几率。首先采用随机取值对种群中的粒子进行初始化，令p(M=0)={xij}，i和j的取值范围分别为1～N和1～D；然后对种群进行反向初始化，p′(M=0)={x′ij}，x′ij可以表示为

x′ij=xmaxj+xminj-xij，

(10)

式中：xmaxj，xminj分别为粒子在第j个维度位置的最大值，最小值；最后选取xij和x′ij中相应位置的最小值作为种群的初始位置。

4)对(6)式中的粒子位置更新方式进行优化，令

(11)

(12)

w′ij=1-wij，

(13)

由于本文以准确提取轴承故障特征为目的，因此利用前3阶故障特征频率占比p作为适应度值选取最优参数，设f1，f2，f3分别为轴承故障的特征频率及其2，3倍频，可将p定义为

(14)

式中：S为输出信号yn的包络谱。

2 互相关谱

由于强背景噪声的存在，通过MCKD得到的解卷积信号中仍然包含较强的噪声干扰，影响故障特征的准确提取和识别，因此，基于互相关分析能够突出不同信号中的相关频率成分且抑制不相关成分的特点，并利用teager能量算子突出信号中瞬态成分的优势，将解卷积信号的teager能量算子和包络进行互相关计算。由于这2类信号中均包含轴承故障产生的特征频率成分，通过互相关计算能够增强故障特征频率成分，抑制随机噪声和不相关的频率成分。

解卷积信号yn的包络可以通过希尔伯特变换获得，即

(15)

式中：Ev(yn)为包络信号；H{·}为希尔伯特变换。

零均值的包络信号可以通过去除均值获得，即

Evzm(yn)=Ev(yn)-mean[Ev(yn)]。

(16)

对于离散信号yn，其teager能量算子可以表示为[15]

φ(yn)=(yn)2-yn+1yn-1，

(17)

类似的，零均值teager能量算子可以表示为

φzm(yn)=φ(yn)-mean[φ(yn)]。

(18)

将包络与teager能量算子这2类信号进行互相关计算并标准化可得

R(m)=

(19)

随后，对互相关分析结果进行快速傅里叶变换，即可得到互相关谱，通过寻找谱图中与滚动轴承理论故障特征频率值相近似的谱线，即可判断滚动轴承的故障类型。

3 故障特征提取流程

提出了一种改进的最大相关峭度解卷积方法，将自适应MCKD与互相关谱相结合以实现滚动轴承复合故障特征的准确分离和提取，算法的流程如图1所示，具体步骤如下：

图1 滚动轴承复合故障特征提取流程Fig.1 Flowchart for compound fault feature extraction of rolling bearing

1)利用传感器采集滚动轴承故障信号，通过滚动轴承的几何参数计算各零件的故障特征频率。计算时MCKD的周期T=fs/f(fs为信号的采样频率，f为故障特征频率，T的初始值设为提取轴承内圈故障特征的周期)。

2)对原始振动信号进行标准化，将滤波器长度L和移位数M的搜索范围分别确定为2～500和1～7，且取值为整数，并以最大故障特征频率占比p为适应度值，借助改进的粒子群算法选取最优滤波器长度和最佳移位数。

3)基于最优[L，M]获得最佳解卷积信号。

4)计算解卷积信号的teager能量算子和包络并获取互相关谱，提取出滚动轴承故障特征。

5)更改周期T(按提取外圈、滚动体故障的顺序)，重复步骤2至4直至提取出试验轴承的全部故障特征，实现滚动轴承复合故障诊断。

4 仿真信号分析

为验证本文所提滚动轴承复合故障诊断方法的有效性，构造了包含内、外圈复合故障的滚动轴承振动仿真信号，其模型为

式中：y1(t)，y2(t)分别为轴承内、外圈故障产生的周期性冲击信号；内圈和外圈故障特征频率分别设定为fi=1/T1=180 Hz，fe=1/T2=115 Hz;Ai为以1/fr为周期的幅值调制，转频fr=30 Hz；ti为第i个周期内由滚动体滑移引起的延迟，ti=(0.01～0.02)T；B(t)为谐波成分，用于模拟信号中存在的干扰成分，f1，f2分别取75，55 Hz；fn1和fn2为共振频率，分别取3 000，2 000 Hz；n(t)为模拟的白噪声，可以通过MATLAB中的函数randn(1,n)获得。

采样频率设置为16 384 Hz，仿真时长为1 s，该仿真信号的时域波形和包络谱如图2所示，包络谱通过对原始振动信号直接进行希尔伯特变换和快速傅里叶变换获得。受背景噪声的干扰，时域波形中未能展现出周期性的冲击成分；包络谱中则仅能识别到轴承外圈故障特征频率fe，轴承内圈故障特征频率fi及其3倍频，噪声干扰较为明显，分析效果不佳。

图2 仿真信号Fig.2 Simulation signal

依据本文提出的方法分析该仿真信号，其中改进粒子群算法的基本参数见表1。

表1 改进粒子群优化算法的参数表1 Parameters for improved PSO algorithm

由仿真信号的分析结果可知(图3左、右列分别对应于内、外圈故障信号，下同)：

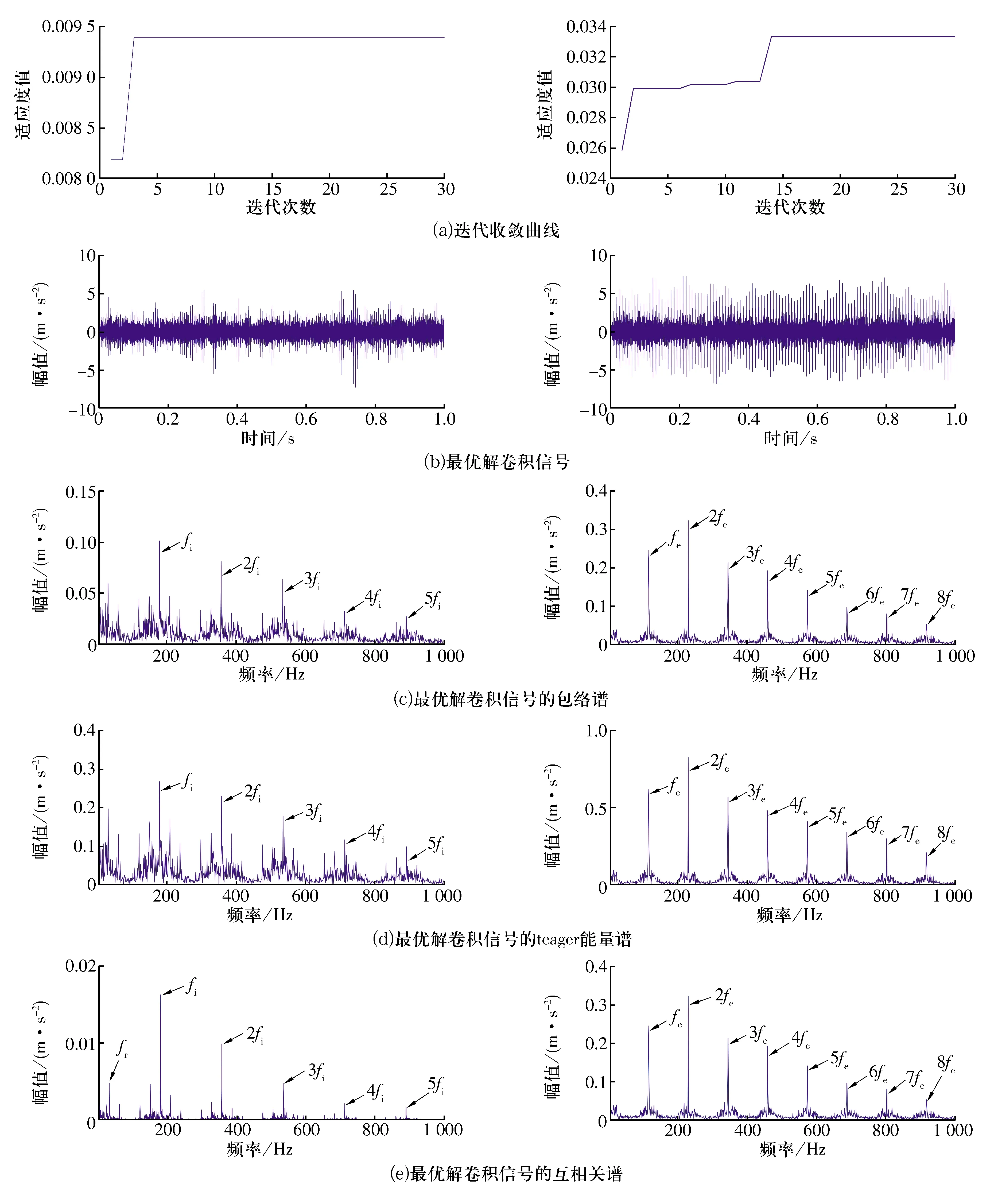
图3 基于本文算法的仿真信号分析结果Fig.3 Analysis results of simulation signals based on algorithm in this paper

1)对于内圈故障，在第3次迭代就取得了最大适应度值0.009 4，此时对应的粒子位置为[208，1]，将其作为MCKD的滤波器长度和移位数值得到最优解卷积信号，最优解卷积信号的包络谱与teager能量谱中虽然能够识别出轴承内圈故障特征频率及其倍频成分，但特征频率及其倍频处的幅值不够突出，存在一定的干扰频率成分；与之相比，最优解卷积信号的互相关谱中噪声干扰明显减弱，从中能够准确识别出转频30 Hz，轴承内圈故障特征频率180 Hz及其倍频成分，说明利用互相关谱能够突出故障特征频率成分，抑制无关随机噪声的干扰。

2)对于外圈故障，当迭代次数为14时，适应度函数可以取到最大值0.033，此时对应的粒子位置为[323，1]，以该粒子位置作为最优参数得到最优解卷积信号，同样，最优解卷积信号的互相关谱中几乎没有噪声的干扰，轴承外圈故障特征频率及其倍频成分更加清晰。

综上分析，可以判断该轴承存在内圈和外圈故障，证明了本文所提方法可以在强噪声干扰条件下有效分离和提取轴承复合故障特征。

5 试验数据分析

为进一步验证所提方法的有效性，利用试验台获取真实的滚动轴承故障信号进行分析。试验台的具体结构如图4所示，包含轴承支承结构、加载装置以及润滑系统等，试验轴承位于支承结构内侧。由于在实际工程测试中，振动传感器难以布置到靠近故障轴承的位置，为模拟真实的信号传递路径，试验过程中将测点选在远离故障轴承的支承结构外侧，振动信号的测量方向为径向。

图4 试验台Fig.4 Test rig

试验轴承型号为NSK 7010C，通过激光切割方法分别在轴承内、外圈沟道面上切一个宽0.2 mm，深0.2 mm，与轴线平行的窄缝，用以模拟滚动轴承存在复合故障的情况，轴承的具体参数见表2。轴承转速为3 000 r/min，信号的采样频率为32 768 Hz。计算可得轴承内、外圈故障特征频率分别为fi=536.4 Hz，fe=413.6 Hz。

表2 测试轴承参数Tab.2 Parameters of test bearing

实测信号及其包络谱如图5所示，由于受到多故障的相互干扰以及复杂传递路径的影响，标准化处理后的时域波形中无法观察到轴承故障导致的周期性冲击成分。包络谱中虽然能够识别出fe及其3倍频，但2fe以及fi，fr等成分则不够明显，且包络谱中频率成分较为复杂，干扰频率较多，故障特征提取效果欠佳，说明仅通过经典的包络分析无法判断轴承的故障状态。

图5 实测轴承故障信号Fig.5 Measured fault signals of bearing

利用本文提出的算法对实测滚动轴承故障信号进行分析，结果如图6所示，由图可知：

1)通过改进的粒子群算法(参数与仿真一致)对MCKD的参数进行自适应选取，提取内圈故障时的移位数和滤波器长度分别为3和498，提取外圈故障时的移位数和滤波器长度分别取为1和393。

2)相比于原始信号，经MCKD处理所得解卷积信号中的噪声成分明显减少。

3)最佳解卷积信号的互相关谱中，fr，fi，2fi，3fi及其两侧间隔为转频的调制边频带均得到了准确表征；fe及其2～4倍频也得到了准确提取，噪声干扰得到了明显抑制。

综上分析可知，该轴承存在内、外圈复合故障。

为进一步体现所提算法的有效性，利用文献[10]的方法处理该实测信号，分析可得提取轴承内、外圈故障特征所用的最佳参数组合分别为[496,2]和[445,1]，结果如图7所示(左、右列分别对应内、外圈故障信号)。对比图6e可知，文献[10]所得结果的噪声干扰要相对明显，部分特征频率成分不够突出，更加体现出本文所提算法在抑制背景噪声，分离和提取轴承复合故障特征中的优越性。

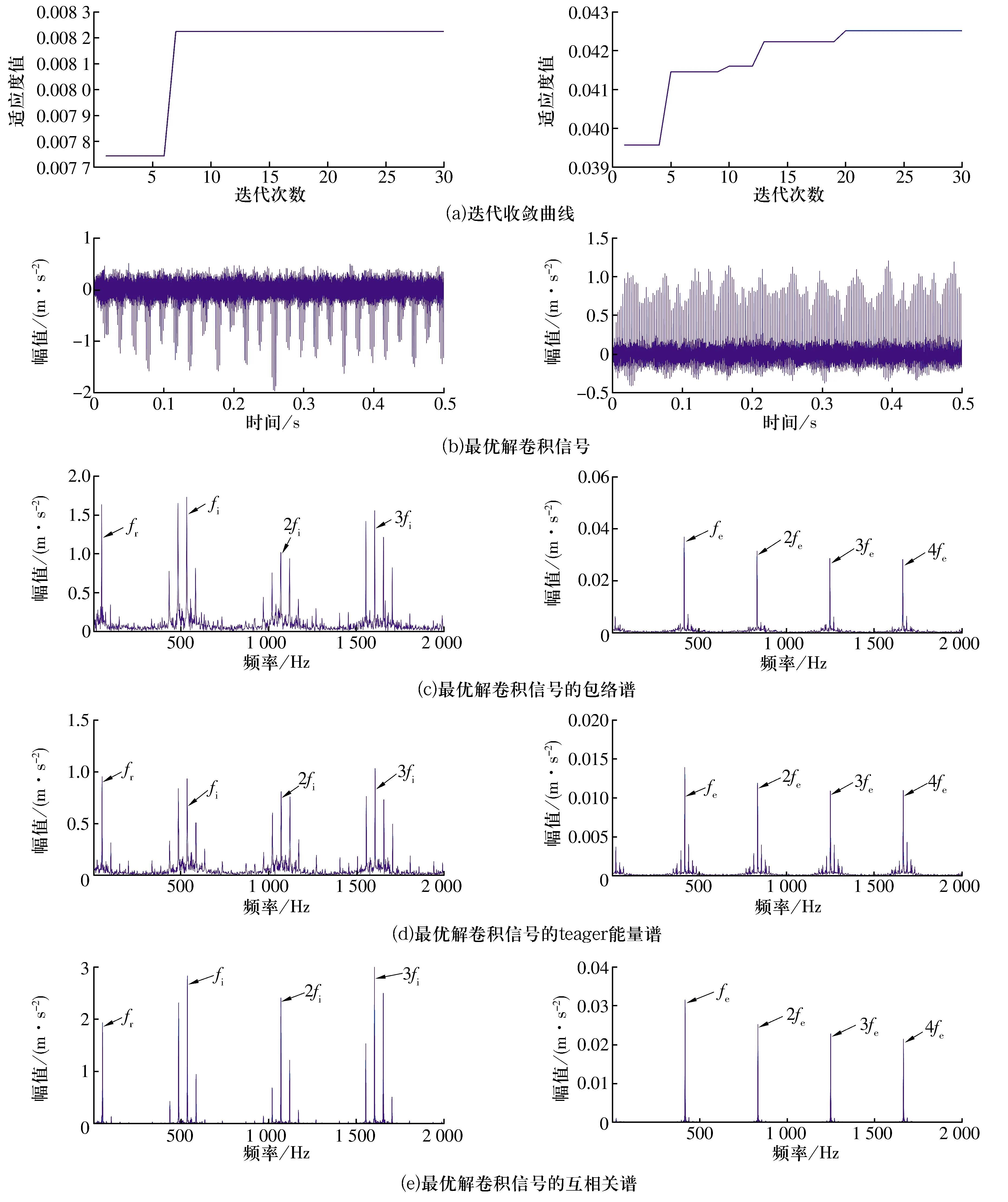
图6 基于本文算法的实测信号分析结果Fig.6 Analysis results of measured signals based on algorithm in this paper

图7 文献[10]方法的分析结果Fig.7 Analysis results based on method in Ref.[10]

6 结论

1)受到背景噪声和多故障特征相互干扰的影响，滚动轴承复合故障特征的分离和提取相对困难，经典的包络分析方法难以取得较好的效果。利用MCKD方法的优势和特点，可以实现多故障特征的分离。

2)以最大故障特征频率占比为指标，借助改进的粒子群算法对MCKD中的滤波器长度和移位数进行优化选取可以避免参数选取的盲目性，保证算法结果的有效性。借助互相关谱可以进一步抑制信号中的无关成分，突出故障特征。

3)仿真和试验信号的验证表明，将MCKD与互相关谱相结合，能够在强背景噪声干扰下提高MCKD的故障特征提取和噪声抑制能力，进而实现更为有效的滚动轴承复合故障诊断。