旋流分离器内流动特性的模拟分析研究

文海龙，李 巍，沈志恒，程新宇，徐 峰，方 堃

(海洋石油工程股份有限公司，天津 300451)

旋流分离器具有结构简易、制造及维护费用低等特点，已成为目前工业分离、除尘设备较为常规的设备，其在工业上的应用已有百余年的历史[1]。在旋流分离器装置中，要求能在低颗粒浓度下高效地分离出最小颗粒，因此为了设计出性能优良的旋流分离器，详细了解其内部的流场分布是相当必要的。

对于湍流流场的数值研究，湍流模型的选取是关键。现有的湍流数值模拟方法包括直接数值模拟、雷诺平均模拟和大涡数值模拟等三种方法。直接数值模拟方法需要较大的计算机内存和耗时较长的计算量，其适合于计算雷诺数较低的简单湍流运动；雷诺平均模拟方法只能提供湍流的平均信息，其没有普适性；大涡模拟方法在较为复杂流动模拟中可以获得湍流流动的细微结构和流动图像，因此该方法被广泛认为是一种非常有前景的湍流数值模拟方法[2]。

对于旋流分离器内部流场的模拟，很多学者采用稳态方法并认为旋流分离器有明确的进出口边界条件，而且认为在稳态下可以大大缩短计算时间。他们采用标准的k-ε模型，RNGk-ε模型及RSM湍流模型对旋流分离器内三维流场进行模拟研究[3-4]。有学者提出在非稳态下进行模拟更能符合旋流。

分离器内部流场的流动情况，这是因为旋流分离器内部实际的气流场是强旋湍流场，湍流的一个重要特征就是随机性，即流体中的各种物理参数，如速度、压力等都随时间与空间发生随机变化，即旋流分离器内部的流场是非稳态的，只是趋向于稳态发展，因此采用非稳态下模拟的气相流场与实际的气相流场更加吻合[2]。近年来，随着计算机处理性能的大幅度提升，在非稳态下对旋流分离器内部强旋流湍流场进行模拟已经成为可能。为此，针对旋流分离器内三维强旋转、且具有明显各向异性的湍流的特点，文章在非稳态下采用大涡数值模型(LES)对旋流分离器内的三维流场进行了模拟计算，并将模拟结果与实验实测数据进行对比和分析。

1 大涡模型(LES)

LES方法是介于直接模拟和雷诺平均模拟法之间的一种场模拟方法。大涡模拟的基本思想是把包括脉动在内的湍流瞬时运动通过某种滤波方法分成大尺度运动和小尺度运动, 大尺度运动通过求解微分方程直接求出来，小尺度运动对大尺度运动的影响通过次网格模型来模拟[2]。

在LES方法中，通过使用滤波函数，每个变量都被分成两部分。滤波函数处理瞬时状态下的N-S方程和连续方程，有：

(1)

(2)

式(1)和式(2)构成了在LES方法中使用的控制方程组，式中带有上划线的量为滤波后的场变量，式(1)中：

(3)

式中，τij定义为亚格子尺度应力。

文章采用Smagorinsky最早提出的亚网格尺度(SGS)模型，对各流场瞬时变量在网格尺度上进行区域平均，可得到平均形式的三维N-S方程组如下：

(4)

动量守恒方程：

(5)

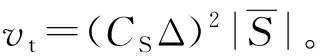
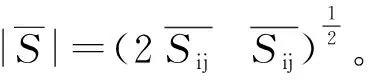
2 物理模型

模型是根据Giulio Solero[6]的实验模型设立，如图1。

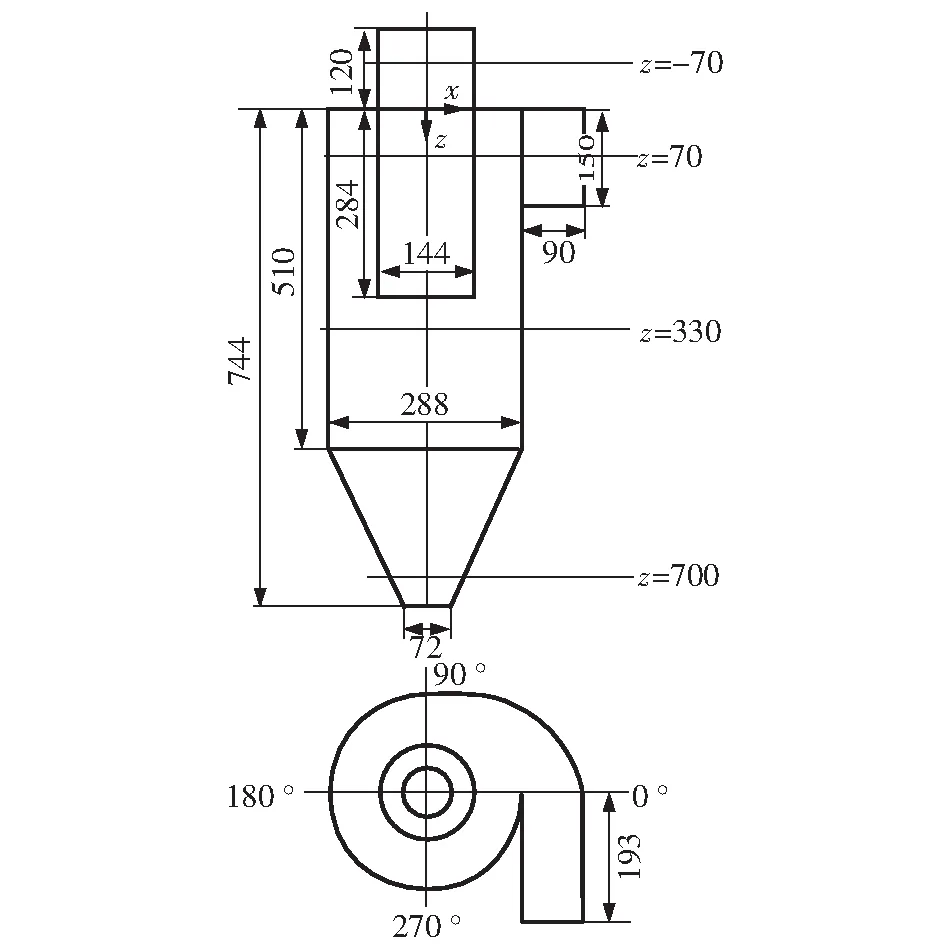
图1 蜗壳式旋流分离器几何结构Fig.1 Geometric structure of spiral case cyclone separator

3 边界条件和模拟参数

(1)入口边界。取入口为常温下的空气，入口速度为6.5 m/s；

(2)出口边界。设置出口边界为Outflow。因排尘口几乎没有气流流出，所以排尘口的流量权重为0, 排气口的流量权重为1；

(3)固壁边界。壁面为无滑移边界条件，湍流采用壁面函数法。

模拟计算中的数值参数如表1。

表1 模拟参数Tab.1 Simulation parameters

4 计算结果及分析

切向速度和轴向速度是旋流分离器内部流场的两个重要参数。切向速度使颗粒具有离心力而分离，而轴向速度则吹着颗粒向灰斗流动而将其捕获。切向速度和轴向速度反映了旋流分离器内部气流的流动特性，因此文章着重分析气流的切向速度和轴向速度，并将模拟值与文献[6]中的试验数据进行对比和分析。图2为非稳态下对气相流场采用采用LES模型得到的速度矢量分布。

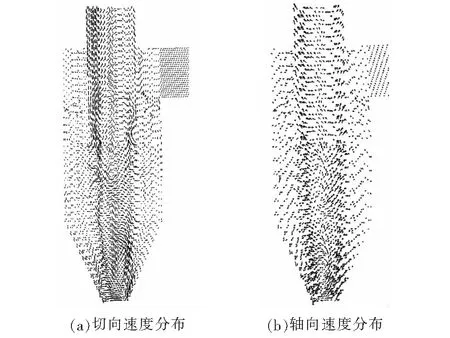
图2 非稳态下的速度矢量分布Fig.2 Velocity vector distribution in unsteady state

从图2中可以看到旋流分离器流场内部的准强制涡和外部的自由涡，且内涡与外涡的交界面很清晰。另外，气相流场在圆筒段的对称性比较好，而在圆锥段的对称性则较差，并出现摆尾现象，这与许多学者的研究结果相吻合，这表明在非稳态下采用LES模型可以很好地预测旋流分离器内部流场的流动特性。下面就在不同径向角度及不同横截面处的切向和轴向速度分布特点加以模拟分析。

(1)环形区域。

图3为沿径向10°、100°两个方向，在z=70 mm高度处的模拟结果与实验结果的切向速度对比图。可以看出,切向速度由外向内逐渐增大，除了壁面附近，可以认为符合准自由涡分布。切向速度在两侧壁面附近下降较大，说明壁面附近速度梯度很大，形成一个速度剪切层，从而极易形成壁面二次涡，且速度“剪切层”对具有粘附性的颗粒在排气管外壁的沉积有重要的影响。图3(a),切向速度值在排气管外壁处达到最大值，同时在另一点处也存在一个极大值，而非沿半径方向一直减小，这主要是因为在蜗壳区域内的两股气流相互作用的结果，一股是排气管壁面附近上升的主气流，另一股则是入口气流。两股气流的相互作用，扰乱了主气流的稳定性，从而切向速度产生震荡波动，使得速度场规律性变差。

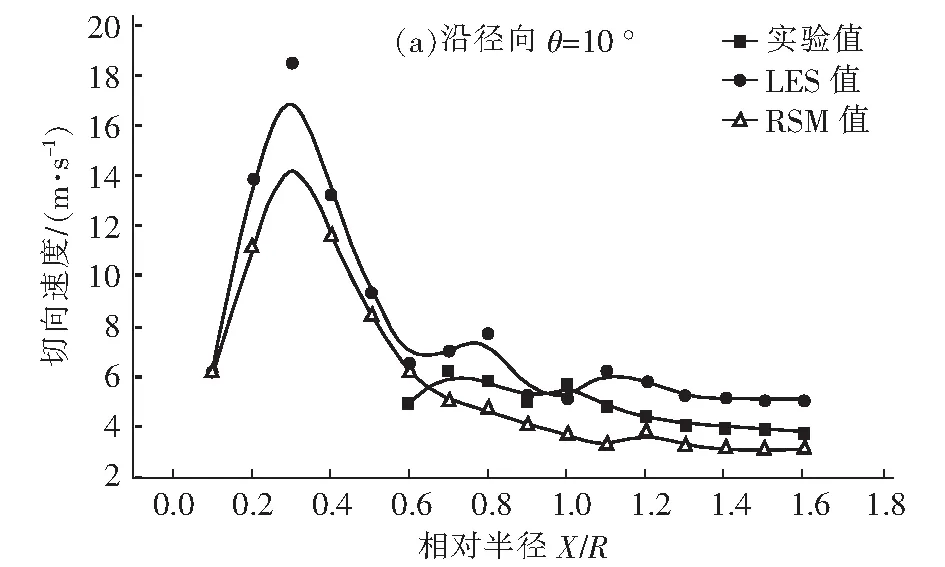
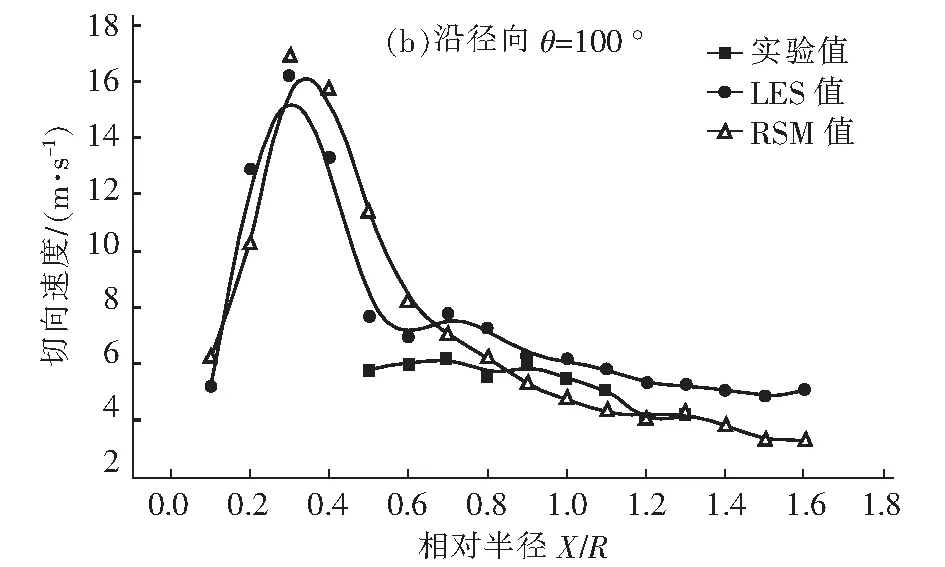
图3 z=70 mm截面处沿不同径向方向的切向速度分布Fig.3 Tangential velocity distribution along different radial directions at z=70 mm

另外，比较图3(a)、图3(b)发现，切向速度分布在环形空间是非轴对称的，在10°方位纵剖面的值明显高于在100°方位纵剖面的值。主要是因为从0°方位纵剖面到90°方位纵剖面，蜗壳式旋流分离器的环形空间的径向宽度逐渐缩小，促使切向速度加大；而从90°到270°，环形空间的径向宽度不变，使得气流向下进入分离空间造成切向速度减小。文章还采用RSM湍流模型也进行模拟计算，计算结果与LES模型模拟计算结果及实验数据吻合较好。

(2)圆筒区域。

图4为θ=180°-0°纵剖面上，切向速度和轴向速度在Z=330 mm高度处的LES模拟值和RSM模拟值与实验值的对比图。从图4中不难看出，正如所预料的那样，在旋流分离器的速度场中, 切向速度起着主导作用，某点处的切向速度值大于其轴向速度值，固体颗粒在切向气流作用下作高速旋转运动，在离心效应下被甩向分离器壁面而被分离出来。预报结果显示切向速度为Rankine涡结构，轴对称性较好，呈现典型的强旋流动特征。轴向速度预报值与实测值符合，在轴线上呈单峰形，流场分为外侧下行流与内侧上行流两个区域，轴对称性较好。

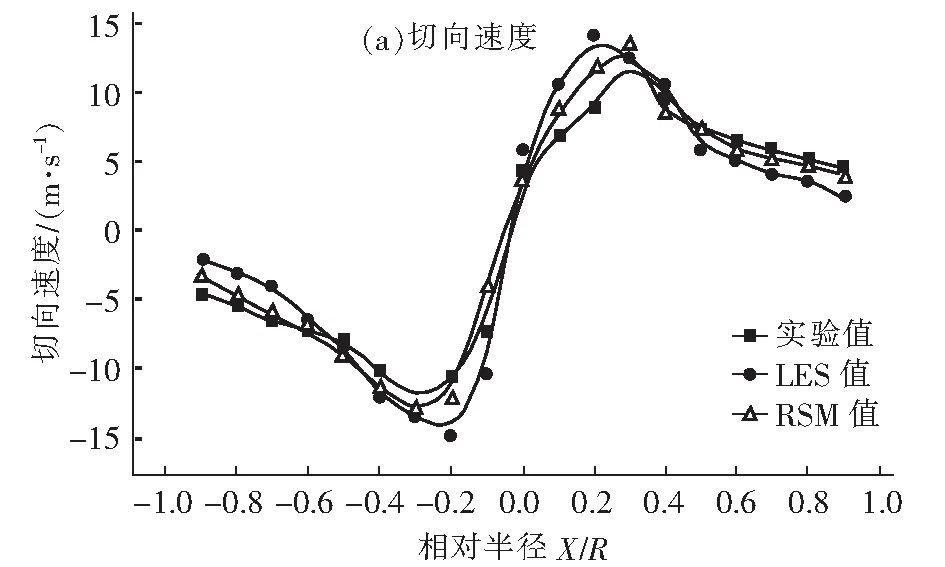
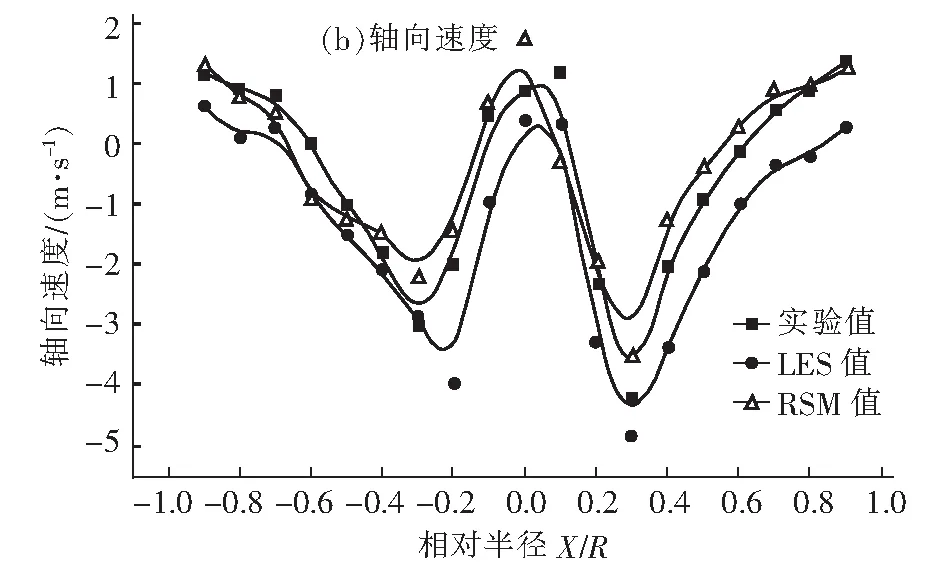
图4 z=330 mm截面处的速度分布Fig.4 Velocity distribution at z=330 mm section

(3)圆锥区域。

图5为θ=180°-0°纵剖面上，切向速度和轴向速度在z=700 mm高度处的LES模拟值以及RSM模拟值与实验值的对比图。从图中可以看出，在锥形区域内，LES模型模拟所得结果更加接近于实验值。这是因为在旋流分离器锥形区域内，气流流动速度的变化较慢，需要较长的时间来对锥形区域内气流流场进行模拟，模拟时间越长，LES的模拟结果越好，故此，LES模型更能很好地模拟出此区域内强制涡中心涡流的流动特性。

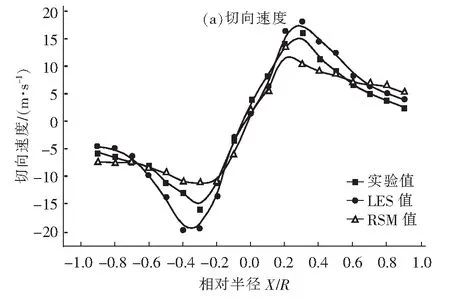
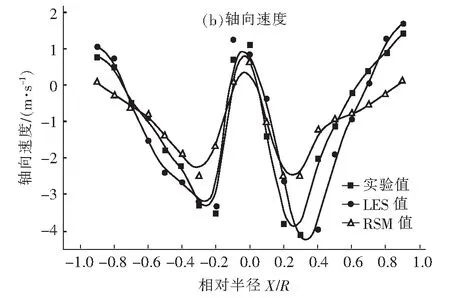
图5 z=700 mm截面处的速度分布Fig.5 Velocity distribution at z=700 mm section

另外,图5(a)预报值和实测值都显示,在圆锥形区域内的下端部分，正切向速度值明显比其他区域的要大，也就是雷诺正应力值比其他区域的要大。这是因为圆锥形区域内的下端部分即排尘口附近,外层的下行气流在分离器底部向上折返时，流线急剧变化，一部分气体会进入分离器底部的排尘口中，受壁面摩擦的影响，这部分气体的流速将减小，而后又会返回分离器的锥体下端，与该处高速旋转的内漩流混合，产生强烈的动量交换和湍流能量耗散，形成偏心环流。另外，由于内漩流的中心线和分离器的中心线并不完全重合，倾斜的内漩流下端就会呈现“摆尾”现象，周期性地扫到壁面上，形成若干个纵向的偏心环流，它会把已经聚集在壁面附近的颗粒重新夹带到分离器内部的上行气流中去，从而降低了分离器的分离效率，可以通过改变分离器底部结构来减小这一部分损失。

(4)排气管区域。

图6给出了不同计算方法得到的在排气管区域内z=-70 mm横截面处的切向速度(a)和轴向速度(b)分布图。可以看出，排气管区域内的速度分布形态仍然是中心高、边壁附近低,而且切向速度大于轴向速度，起主导作用,说明排气管内湍流仍然是各向异性的。RSM模拟结果和实测的速度结果存在明显的差异，而LES模型却能得到较好的效果。轴向速度分布与排气管以下空间内的分布形态迥异,在旋转流的几何中心,轴向速度很小,但随半径的增大,其值急剧增大,靠近壁面处变化量减小。

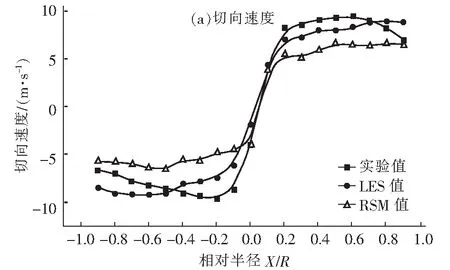
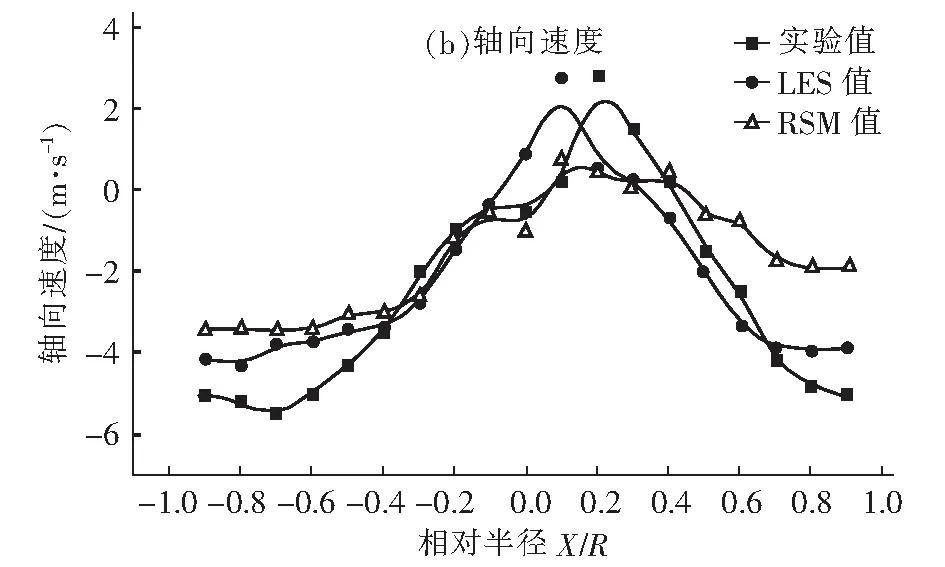
图6 z=-70 mm截面的速度分布Fig.6 Velocity distribution of z=-70 mm section

由图6(b)可以看出,轴向速度的分布并不是沿着旋流分离器的几何中心对称，而是有一定的偏心距离,这表明在排气管区域内存在一个明显的偏离轴心的旋转蜗核区域，同时在排气管末端有气流短路现象存在。由于角动量守恒和和截面积半径的减小，排气管区域中心蜗核区的角速度值ω=Wmax/rmax≈650 rad/s，这明显高于圆环区域中心蜗核区的角速度值(ω≈400 rad/s)。角速度的陡升，促使排气管区域内流场湍流程度增强，存在强制涡中心涡流区，致使RSM模拟结果与实验结果有一定的偏差。

5 结束语

旋流分离器内部进行的是两相流运动，是气相和固体颗粒相的分离过程，而颗粒相属于稀疏相， 固体颗粒的运动在很大程度上还是要取决于分离器内部的气体流场，而速度场是旋流分离器内部最主要的流场。文章采用LES模型对在非稳态下旋流分离器内的三维气相流场的流动特性进行了模拟计算。结果表明:

(1)采用LES模型对旋流分离器模拟计算，得出的结果与实验数据对比分析可知，LES模型可以获得比RSM模型更多的湍流信息，尤其是细微的强制涡中心涡流运动情况的信息。因此，LES模型更能较真实准确的模拟循环旋流分离器内部湍流流场的流动特性。

(2)按照速度场的分布规律可将分离器内部的流动空间外侧下行流与内侧上行流两个区域, 其分界面大致为排气管壁面向下的延长线。在不同的流动区域中, 速度场的分布有较大的不同， 内部区域中切向速度沿径向变化梯度比外部区域中大得多。

(3)旋流分离器内速度分布呈现组合涡的特点，气相流场是双层旋转流, 中心区域强制涡有利于将颗粒甩向外部, 外部准自由涡区有利于颗粒在壁面附近被捕集, 内部旋流压力分布差异导致分离器锥底出现返流现象,这与实际情况相吻合。