带扰动的延迟对偶风险模型的渐近解
申海燕,周国立
(重庆大学 数学与统计学院,重庆 400044)
在对偶风险模型中,公司的盈余过程主要由两部分组成:一是以固定速率的连续支出,二是服从复合Poisson过程的随机收入。1955年,Cramér首次提出了此模型[1]。近年来,对偶风险模型也一直备受关注,如Ng讨论了对偶风险模型的最优分红问题[2]。在一般的对偶风险模型中,更新一发生随机收益就立即到达,但是,许多因素会导致收益存在延迟,因此,一般的对偶风险模型在实际应用中很受限制。
延迟首先被引进了经典风险模型中主要是因为在实际中可能会存在索赔发生了但没有被报道或者索赔被报道了但没有立即执行等情况,例如,Trufin和Waters讨论了有索赔延迟的离散时间的风险过程[3-4]。随着延迟在经典风险模型中的深入研究,带延迟的对偶风险模型也受到了大量重视。对偶模型主要适用于模拟有随机收益的公司的盈余过程,但是在更新转变为收益前通常会存在延迟,例如专利申请中的延迟,在USPTO申请专利的平均等待时间大概是27个月,因此很多公司的随机收益会存在延迟。
然而,一些公司的随机收益不仅会有延迟,它的盈余过程也会由于某些因素(比如期望、利率、通货膨胀等)而存在波动,一般地,将这种波动称为扰动。例如,石油公司的随机收益由于开采过程会有一定的延迟时间,并且石油公司的盈余会因国家政策或者市场调控而上下波动。由此可见,延迟对偶风险模型或者带扰动的对偶风险模型不足以模拟一些公司的盈余过程。1991年,带扰动的经典风险模型首次被Dufresne提出[5],随后,许多学者将扰动引入对偶风险模型中[6-9]。目前,已经有一部分学者研究过带扰动的延迟风险模型[10-11],但很少有学者研究过带扰动的延迟对偶风险模型。
所以,本研究主要考虑将延迟和扰动同时引入对偶风险模型中,此模型不仅是众多学者研究的带扰动的对偶风险模型的推广,还是Zhu所研究的延迟对偶风险模型的推广[12]。本研究主要目的是推导出破产概率和相关破产时间的渐近解。在以往的研究中,一般的方法是运用拉普拉斯变换找到一个二阶积分-微分方程的解,但由于后者是一个二阶积分-偏微分方程,所以此方法并不适用于本研究提出的模型。因此,在文献[12]方法的基础上,本研究运用了另一种新方法解决这个难题,即结合Itô公式,通过构造几类特殊函数同时从放缩法的角度求解渐近解,最后,将结果进行了对比分析。
本研究的结构如下:第一节介绍了带扰动的延迟对偶风险过程。第二节推导出了最终生存概率满足的积分-偏微分方程,同时计算出了破产概率的渐近解。第三节主要得到了有关破产时间的渐近解。第四节主要讨论了在延迟时间是有界的条件下的显示解。第五节主要是数值模拟实验和比较分析。第六节给出了一些结论。
1 带扰动的延迟对偶风险过程
首先考虑一个带布朗运动扰动的对偶风险模型,其盈余过程定义如下:

定义τ为盈余过程第一次到达0的时间,即:τ= inf{t> :Xt≤0},假设此盈余过程满足正电荷条件:

文献[7]中给出了有限区间内的破产概率为:P(τ < ∞|X0=x)=e-αx,其中,α是下列方程的唯一正根:

当随机收益没有延迟时,假设{Tk-Tk-1}k≥1是独立同分布的参数为λ的指数分布,则收益的过程是一个参数为λ的泊松过程。然而当收入存在延迟时,假设是Lk独立同分布的非负随机变量,累积分布函数为L(t),并且定义(t)= 1-L(t)。
在上述的带扰动的延迟对偶风险模型中,时刻t≥0之后的破产时间仍定义为盈余过程首次到达0的时刻,即τt= inf(s:s≥t,Xs≤0)。若破产没有发生,则τt= ∞,相应地在时刻t的最终破产概率为ψ(x,t)=P(τt<∞|Xt=x),以及在时刻t的最终生存概率为φ(x,t)= 1-ψ(x,t)。
我们注意到,一个带延迟的泊松过程仍然是一个泊松过程,文献[14]中证明了这一结论。并且文献[13]也更为详细地指出了带延迟的Nt在t时刻是一个参数为λL(t)的泊松过程。
2 破产概率的渐近解
本节首先推导出了最终破产概率满足的积分-偏微分方程,然后利用Itô公式得到了破产概率的上、下界以及渐近解。除此之外还将此模型中破产概率的结果与延迟对偶风险模型中的结果进行了对比。
引理2.1 假设λE[Y1]>ρ,则最终生存概率φ(x,t)满足方程

证明 首先考虑时间t之后的非常小的一段时间Δt。假设Xt=x,则有:
(i)无随机收益发生的概率为1- λL(t)Δt,且Xt+Δt=x- ρΔt+ σBΔt;
(ii)由(i)可以计算出随机收益Y发生的概率为λL(t)Δt,且Xt+Δt=x-ρΔt+Y+σBΔt。
再根据马氏链的性质,有

然后利用Itô公式可以得到
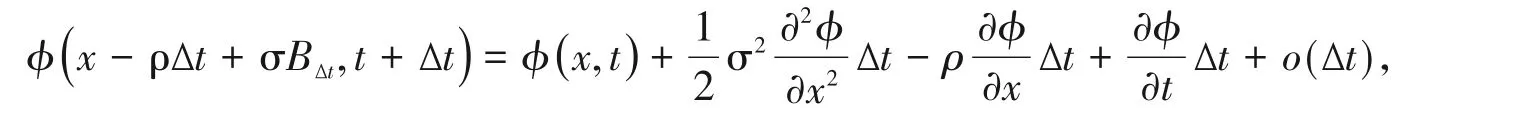
最后将上两式相加并令Δt→0可得到式(4)。
注2.1 如果初始盈余为0,则φ(x,t) ≡0。

其中,α为满足式(3)的唯一正根。特别地,当x→∞时,

当τt< ∞时,破产一定会发生,即Xτt= 0,所以有

再由式(7)和式(8)得

显然,

另一方面,

然后,有

将式(12)代入式(11)得

再根据式(9)和式(13)可得

从式(14)可以推出
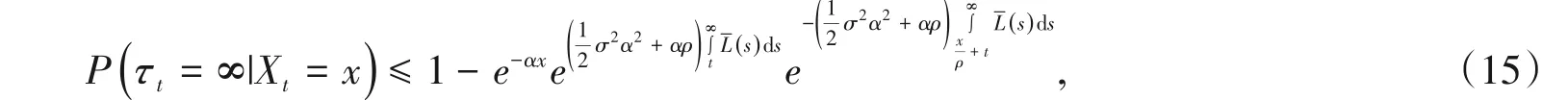
由式(9)、式(10)和式(12)可得

再由式(16)可得

最后根据式(15)和式(17)可得到式(5),再令式(5)中的x→∞可得到式(6)。
注2.2 本研究将扰动引入了延迟对偶风险模型中,再由文献[1]方法的启发,构造了函数w(x,t)和Ltw来解决由扰动带来的困难,发现本研究模型下的破产概率的渐近解与文献[1]中的结果不同。
下面通过一些具体的例子来说明两个渐近解的不同之处。
注2.3 假设p(y)=ve-vy,根据式(3),可以得到

所以上式对λ求导可得

3 破产时间的渐近解
本节的目标是获得破产时间期望值的上下界以及它的渐近解。但是,如果满足式(2)的条件,那么破产就有可能不会发生,即τt可以为∞,则EXt=x[τt]是无限的。为了使得估计破产时间的期望值有意义,下面假设λE[Y1]<ρ,并且令v(x,t)=EXt=x[τt-t]。在得到这些结果之前,可以做类似于引理2.1的讨论,从而得到v(x,t)满足的积分-偏微分方程。
引理3.1 假设λE[Y1]<ρ,则v(x,t)满足
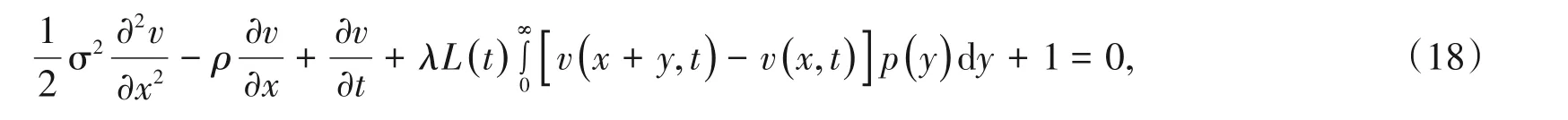
其中v(0,t)≡0。
证明 令q(x,t)=EXt=x[τt],再做类似于引理2.1的讨论,可得到

然后利用Itô公式可以得到
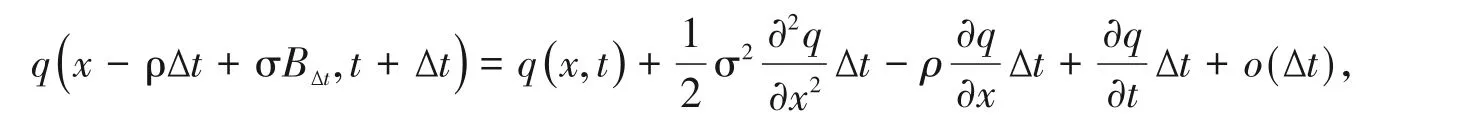
将上两式相加并令Δt→0可得

因为v(x,t)=q(x,t) -t,所以有

最后,得到

并且,如果x= 0,则τt=t,即v(0,t)=EXt=x[t-t]= 0。
接下来主要通过构造函数h(x,t)和Lth来推导出破产时间期望值的渐近解,与第二小节不同的是,它的渐近解不受到扰动项的影响。
定理3.1 假设E[Y1]<ρ,则有

并且当x→∞时,
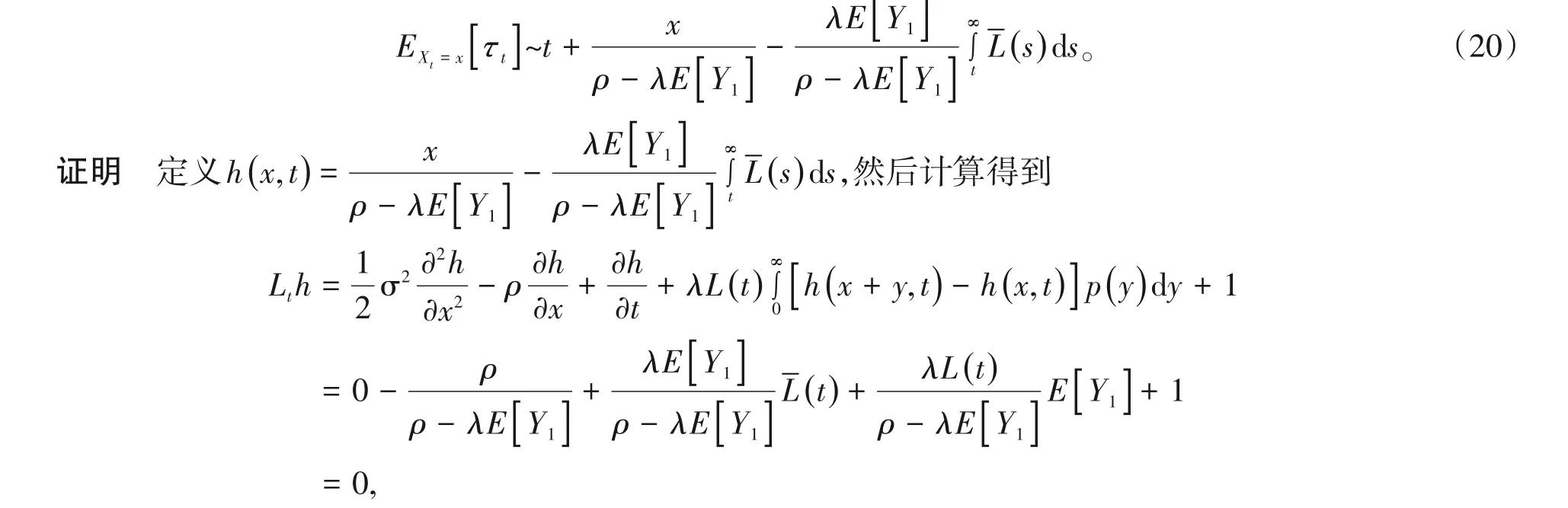
再通过做与文献[1]中的定理2.3的类似讨论可证明式(19)和式(20)。
注3.1 在带扰动的延迟对偶风险模型中的破产时间期望值的渐近解与延迟对偶风险模型中的结果一样。此现象表明在初始盈余非常大的情况下,盈余的小波动不会影响破产时间的期望值。
4 具体可解决的模型
第二节和第三节分别得到了破产概率和与破产时间相关的渐近解。虽然对于得到式(4)的具体解很难,但是在某些特殊模型下可以求出具体解。当延迟时间为有界时,此模型可以求得具体解。假设延迟时间比固定时间l短,即

定理4.1 假设延迟时间满足式(21),则ψ(x,t)满足

证明 (i)首先考虑t 再利用Itô公式可以得到 结合上两式并令Δt→0可得式(22)。 (ii)接下来考虑t≥l时的情况。此时,在时间[t,Δt]内,有收益的概率为λLΔt,无收益的概率为1-λLΔt。类似引理2.1,由马氏链的性质可得 最后将上两式相加并令Δt→0可得到式(23)。 注4.1 当x= 0时,ψ(0,t)= 1。 定理4.2 假设延迟时间满足式(21),则有 其中,α为满足式(3)的唯一正解。 证明 在此条件下,破产概率满足式(22)和式(23)。当t≥l时,在时刻t没有延迟发生。即为一般的对偶风险模型的破产概率,ψ(x,t)=e-αx,具体求解步骤可参考文献[6]。如果t 令f(x)=e-αx,并且定义 再根据Dynkin′s公式可得 即 将式(25)中的l取值为t,则有g(t)=e-αx,再令g(l)对l求导有 注4.2 当t 本节主要进行数值模拟实验,并且根据实验结果来说明扰动对于延迟对偶风险模型中的破产概率的影响。 首先假设当t< 1时,L(t)=t;t≥1时,L(t)= 1(即l= 1),p(y)=re-ry,由定理4.2得 然后令ρ=σ=r= 1,Bl= 0.05,λ= 2,最后得到在时间t= 0.35、t= 7、t= 1.05和t= 1.4时的给定不同初始盈余值(初始盈余值x=0.2、0.4、0.6、0.8、1.0、1.2)下的破产概率(详细结果见表1)以及相关图形(见图1)。同时,还将本节中的破产概率与延迟对偶风险模型下的破产概率进行了比较(参数的取值都相同)。延迟对偶风险模型下的破产概率解的形式可参见文献[1],最后模拟的具体结果见表2和图2。 表1 带扰动的延迟对偶风险模型下的破产概率Table 1 The ruin probability under the delayed dual risk model with diffusion 表2 延迟对偶风险模型下的破产概率Table 2 The ruin probability under the delayed dual risk model 图1 带扰动的延迟对偶风险模型Figure 1 The delayed dual risk model with diffusion 图2 延迟对偶风险模型Figure 2 The delayed dual risk model 注意:表1与表2中的NA并不意味着破产概率不存在,而是目前没有具体解的形式。根据表1、2和图1、2,我们发现带扰动的对偶风险模型和延迟对偶风险模型的破产概率在t>l时仅依赖于初始盈余值x,并且随着初始盈余值的增加而减小。除此之外,在t 本研究基于文献[1]中的延迟对偶风险模型构建了带扰动的延迟对偶风险模型,通过构造几类特殊函数,并结合Itô公式和积分-偏微分方程推导出破产概率和有关破产时间的渐近解,然后在某些特定条件下求得了破产概率的显示解,最后通过数值实例说明了扰动会使得延迟对偶风险模型下的破产概率变大,并且在时间t小于延迟时间时,带扰动的延迟对偶风险模型下的破产概率随时间的增长而变大,延迟对偶风险模型下的破产概率随时间的增长而减小。这对某些公司降低破产概率有参考价值。此模型还可以拓展为随机收益为Erlang分布、增加跳或者Lėvy过程以及扰动是随机的情况,这需要更深入的研究。





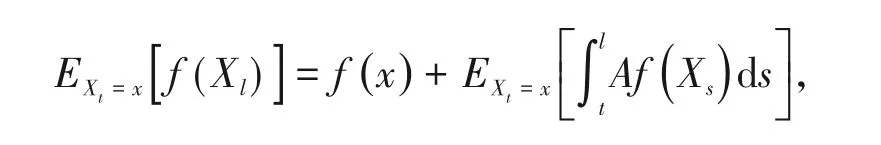


5 数值实例
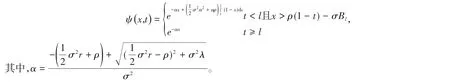




6 结论

